Displacement Current

The story of displacement current begins with a brilliant 19th-century scientist named James Clerk Maxwell. He was a Scottish physicist who made significant contributions to the field of electromagnetism. In 1861, Maxwell was working on understanding how electric and magnetic fields interact. He was studying the behavior of electric fields in capacitors, which are devices used to store electric charge.

At that time, scientists knew about the electric current that flows through wires—this is the current that lights up bulbs and powers motors. However, they were puzzled by what happens in a capacitor. A capacitor consists of two metal plates separated by an insulator (like air or another material). When a capacitor charges, electric fields develop between the plates, but no actual charge flows through the insulator. This was a mystery because the established laws of electromagnetism, specifically Ampère’s circuital law, seemed to suggest that a current should be there to create the magnetic fields they observed around the capacitor.

Maxwell proposed a bold idea in his paper “On Physical Lines of Force, Part III” in 1861. He suggested that even though there is no flow of charge between the capacitor plates, the changing electric field itself could be thought of as a current. This “current” wasn’t made of moving charges but was a result of the changing electric field. He called this the displacement current.

Maxwell added this displacement current to Ampère’s circuital law, which before only considered currents of moving charges. This addition was crucial because it helped explain the magnetic fields around capacitors and also led to the prediction of electromagnetic waves—waves of electric and magnetic fields that travel through space.

In 1865, Maxwell used his amended version of Ampère’s law to derive the electromagnetic wave equation, which showed that light itself is an electromagnetic wave. This was a groundbreaking discovery that united the fields of electricity, magnetism, and optics into one single theory.

The introduction of the displacement current was a key step in the development of Maxwell’s equations, which are the foundation of classical electromagnetism. These equations describe how electric and magnetic fields are generated and altered by each other and by charges and currents.

What is Displacement Current?

Displacement current is a concept introduced by Maxwell to explain how changing electric fields can generate magnetic fields, just like actual currents do. It is essential to understand the complete picture of how magnetic fields are generated, even in situations where there is no actual flow of electric charge (current) through a conductor.

Let’s revisit the situation with the charging capacitor. When a capacitor is charging, there is a current i(t) in the wires leading to the capacitor plates. This current creates a magnetic field around the wire. However, between the capacitor plates, no actual charge flows through the gap. So, according to Ampere’s circuital law, there seems to be no current inside the capacitor, which would imply no magnetic field, leading to a contradiction. We see this contradiction in the following cases.

(a) Determining the Magnetic Field Using a Loop

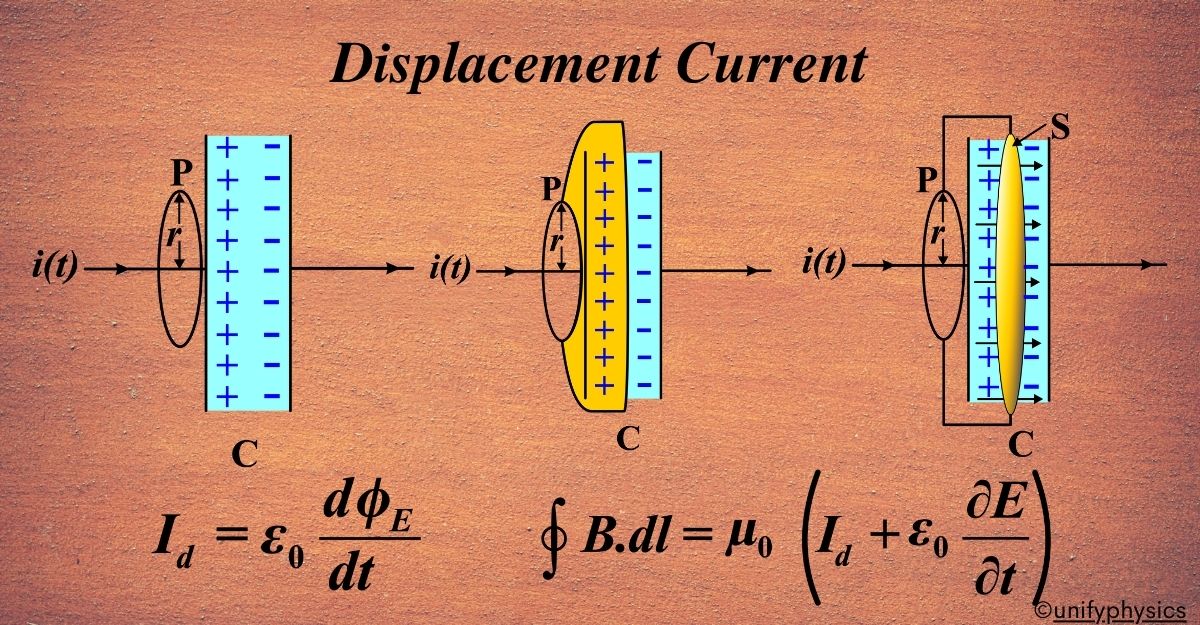
Consider a parallel plate capacitor (C) that is part of a circuit with a time-dependent current i(t). We want to determine the magnetic field at a point (P) outside the capacitor.

For the circular loop, this simplifies to:

\(\displaystyle B \cdot (2\pi r) = \mu_0 i(t) \)

Solving for (B):

\(\displaystyle B = \frac{\mu_0 i(t)}{2\pi r} \)

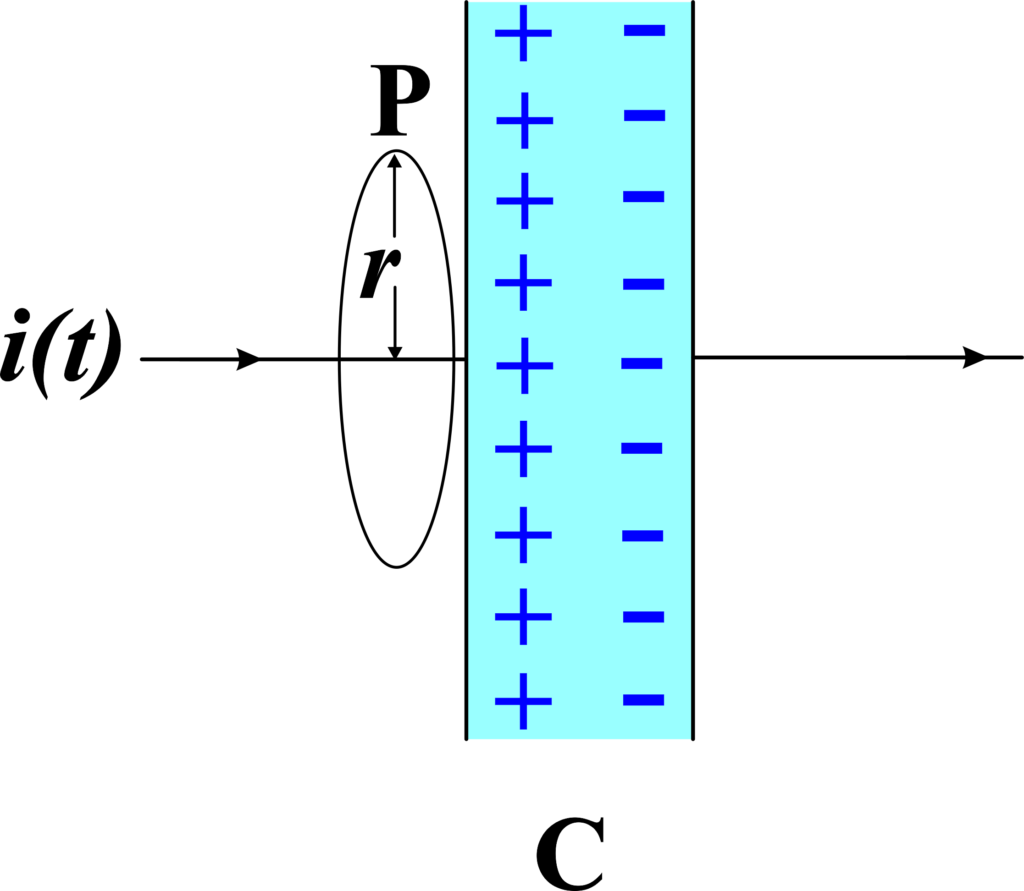
(b) Pot-Shaped Surface Inside the Capacitor

According to Ampere’s circuital law, applying it to this surface would give us:

\(\displaystyle \oint \mathbf{B} \cdot d\mathbf{l} = \mu_0 i = 0 \)

This suggests there is no magnetic field, which contradicts our earlier result using the loop.

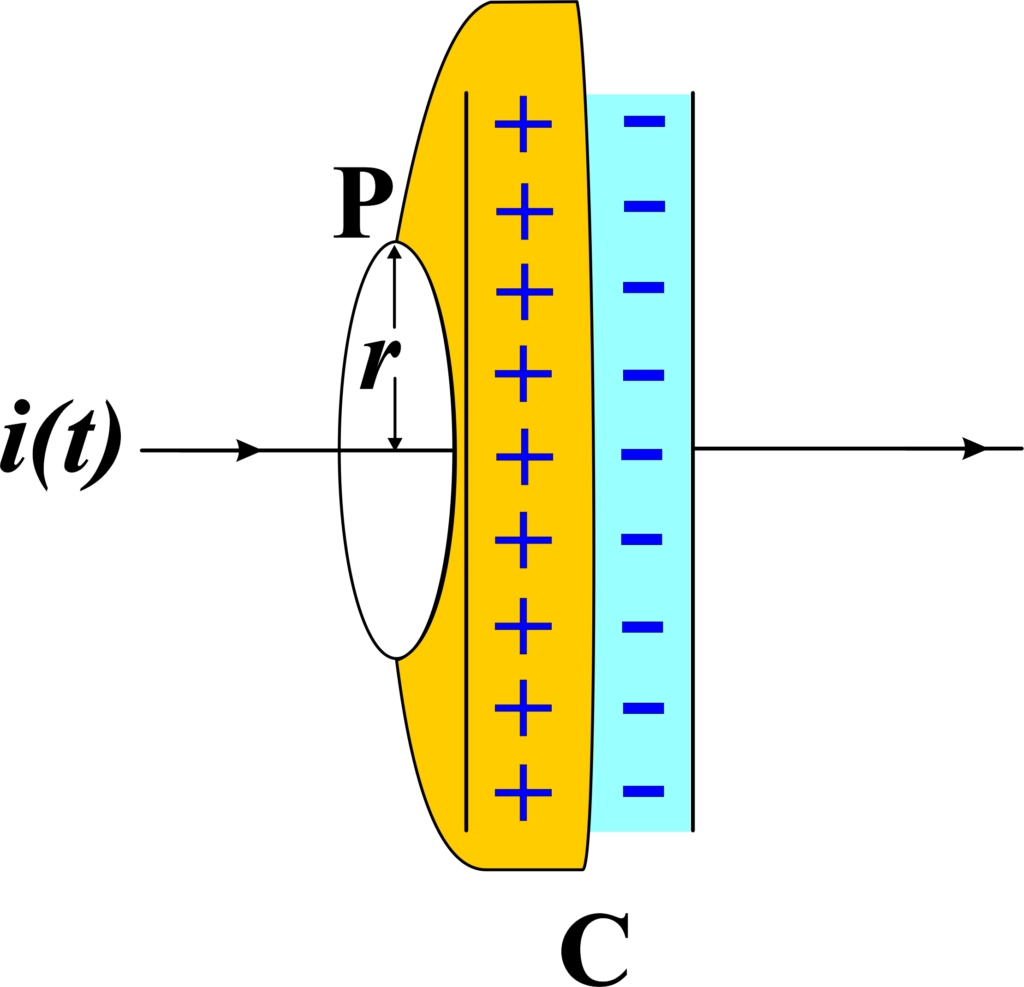
(c) Tiffin-Shaped Surface with Flat Circular Bottom

To resolve this contradiction, Maxwell introduced the idea of the displacement current. Even though no actual charges are moving between the capacitor plates, the electric field between the plates changes as the capacitor charges or discharges. This changing electric field can be thought of as creating its form of current, called the displacement current.

Maxwell’s concept of displacement current is crucial for understanding how a changing electric field can produce a magnetic field, even when there is no actual current flowing through a conductor. Let’s see how Maxwell explains this concept using a parallel plate capacitor (C) as part of a circuit with a time-dependent current i(t).

To understand the missing term, let’s closely examine Figure (c). What is present between the plates of the capacitor? It’s the electric field! If the plates have an area (A) and carry a total charge (Q), the electric field (E) between the plates is given by \(\displaystyle \frac{Q}{A \epsilon_0} \). This electric field is perpendicular to the surface (S) shown in Figure (c). The electric field is uniform over the area (A) of the capacitor plates and is zero outside this area.

Next, we need to determine the electric flux \(\displaystyle \Phi_E \) through surface (S). According to Gauss’s law, the electric flux is the product of the electric field ( E ) and the area (A) through which the field lines pass:

\(\displaystyle \Phi_E = E \cdot A \)

So, in essence, the electric flux through the surface (S) is directly related to the charge (Q) on the capacitor plates and the permittivity of free space \(\displaystyle \epsilon_0\).

Maxwell introduced the concept of displacement current to account for this changing electric field. The displacement current (I_d) is defined in terms of the changing electric field (E). For a capacitor with plates of area (A) and the electric field changes over time, the displacement current is given by:

\(\displaystyle\begin{equation}\label{eqn:1}\boxed{\boldsymbol{I_{d} = \epsilon_0 \frac{d\Phi_E}{dt} }} \end{equation}\)

Since the electric field (E) between the capacitor plates is related to the charge (Q) on the plates by \(\displaystyle E = \frac{Q}{A \epsilon_0} \), the displacement current can be expressed as:

\(\displaystyle I_d = \epsilon_0 \frac{d}{dt} \left( \frac{Q}{A \epsilon_0} \cdot A \right) = \frac{dQ}{dt} \)

Since the actual current i(t) flowing into the capacitor plates is \(\displaystyle i(t) = \frac{dQ}{dt} \), we see that the displacement current (I_d) has the same magnitude as the actual current i(t).

So, the displacement current equation tells us that the displacement current is proportional to how quickly the electric field is changing in the capacitor. When the electric field changes rapidly, the displacement current is large; when it changes slowly or not at all, the displacement current is small or zero. In simpler terms, even though we can’t see charges moving between the capacitor plates, the changing electric field acts as if there’s a current, and this equation helps us calculate it.

Example: a capacitor in a radio circuit. When the radio is turned on, the capacitor charges and discharges rapidly. The changing electric field between the capacitor plates generates a displacement current, which, in turn, creates a magnetic field. This magnetic field is part of the electromagnetic waves (like radio waves) that travel through the air and reach your radio.

Physical Interpretation:

The displacement current isn’t a real current of moving charges, but it acts as if it were a real current in terms of generating a magnetic field. This means that even in regions where there are no moving charges (such as the gap between the capacitor plates), the changing electric field produces a magnetic field.

By adding the displacement current term to Ampere’s circuital law, we get the modified form of the law, known as Ampere-Maxwell law:

\(\displaystyle\begin{equation}\label{eqn:2}\boxed{\boldsymbol{ \oint B \cdot dl = \mu_0 \left( i_{d} + \epsilon_0 \frac{d\Phi_E}{dt} \right)}} \end{equation}\)

This law is consistent in all situations, ensuring that magnetic fields are correctly accounted for, whether they are produced by actual currents or by changing electric fields.

Displacement current completes the picture of electromagnetic interactions and is crucial for understanding phenomena such as electromagnetic waves, which include light, radio waves, and X-rays.

Maxwell-Ampere Law

The total current passing through any surface of which the closed loop is the perimeter is the sum of the conduction and displacement currents. This is also known as – Ampere-Maxwell Law.

The Maxwell-Ampere Law is a fundamental principle that explains how electric currents and changing electric fields can create magnetic fields.

Imagine you’re playing with a magnet and some iron filings. You sprinkle the filings around the magnet, and they align themselves in a pattern that shows the magnetic field. Now, what if you could create that magnetic field without the magnet, using just electricity? That’s where the Maxwell-Ampere Law comes into play.

The Maxwell-Ampere Law is like a recipe for creating magnetic fields. It tells us that electric currents and changing electric fields can produce magnetic fields. This law is a key part of Maxwell’s equations, which are the rules governing electricity and magnetism.

Let’s start with a simple part of the law—Ampere’s Law. It says that if you have an electric current flowing through a wire, it will create a magnetic field that circles around the wire. The strength of this magnetic field is proportional to the amount of current flowing.

Now, Maxwell added a special ingredient to this recipe. He said that not only does a steady electric current create a magnetic field, but so does a changing electric field. This was a groundbreaking addition because it meant that even in places where there’s no actual current flowing, like between the plates of a charging capacitor, a magnetic field can still be created by the changing electric field.

The Maxwell-Ampere Law can be written in a simple form as:

\(\displaystyle\nabla \times \mathbf{B} = \mu_0 (\mathbf{J} + \epsilon_0 \frac{\partial \mathbf{E}}{\partial t}) \)

• \(\displaystyle \nabla \times \mathbf{B} \) is the curl of the magnetic field, which tells us how the field twists and turns in space.
• (µ₀) is the permeability of free space, a constant that tells us how well a magnetic field can spread through the vacuum.
• \(\displaystyle\mathbf{J}\) is the current density, which is how much electric current you have per unit area.
• (ε₀) is the permittivity of free space, another constant that tells us how an electric field affects and is affected by the vacuum.
• \(\displaystyle\frac{\partial \mathbf{E}}{\partial t}\) is the rate of change of the electric field over time.

The Maxwell-Ampere Law is a cornerstone of electromagnetism that extends Ampere’s Law to include the concept of displacement current. Here’s how we can derive it step by step:

Ampere’s Law tells us that the magnetic field (B) around a current-carrying wire is proportional to the electric current (I). Mathematically, it’s written as:

\(\displaystyle\oint \mathbf{B} \cdot d\mathbf{l} = \mu_0 I \)

where \(\displaystyle \oint \mathbf{B} \cdot d\mathbf{l} \) is the line integral of the magnetic field around a closed loop, and (µ₀) is the permeability of free space.

Now, think about a capacitor that’s charging. There’s a changing electric field between the plates, but no actual current flows through the insulator. However, there’s still a magnetic field around the capacitor, which means there must be something equivalent to a current, which we call the displacement current.

Maxwell introduced the displacement current to account for the changing electric field in a capacitor. The displacement current (I_D) is given by:

\(\displaystyle I_D = \epsilon_0 \frac{\partial \Phi_E}{\partial t} \)

where \(\displaystyle \epsilon_0\) is the permittivity of free space, and \(\displaystyle \frac{\partial \Phi_E}{\partial t} \) is the rate of change of electric flux.

To include the displacement current, Maxwell modified Ampere’s Law by adding the displacement current term to the right side of the equation:

\(\displaystyle \oint \mathbf{B} \cdot d\mathbf{l} = \mu_0 (I + I_D) \)

which becomes:

\(\displaystyle \oint \mathbf{B} \cdot d\mathbf{l} = \mu_0 I + \mu_0 \epsilon_0 \frac{\partial \Phi_E}{\partial t} \)

Since the electric flux (Φ_E) is related to the electric field (E), we can express the displacement current in terms of the electric field:

\(\displaystyle \oint \mathbf{B} \cdot d\mathbf{l} = \mu_0 I + \mu_0 \epsilon_0 \frac{\partial}{\partial t} \int \mathbf{E} \cdot d\mathbf{a} \)

where \(\displaystyle \int \mathbf{E} \cdot d\mathbf{a} \) is the electric flux through a surface area \(\displaystyle d\mathbf{a} \).

The final form of the Maxwell-Ampere Law, which includes both conduction current and displacement current, is:

\(\displaystyle \nabla \times \mathbf{B} = \mu_0 \mathbf{J} + \mu_0 \epsilon_0 \frac{\partial \mathbf{E}}{\partial t} \)

where \(\displaystyle \nabla \times \mathbf{B} \) is the curl of the magnetic field, and \(\displaystyle \mathbf{J} \) is the current density.

This law is powerful because it unifies the effects of conduction current and changing electric fields in creating magnetic fields. It’s essential for understanding how electromagnetic waves propagate and is a fundamental principle in classical electrodynamics.

Characteristics of Displacement Current

Think of displacement current as a bit of a magic trick in the world of physics. It’s not current in the traditional sense—no electrons or charges are moving around. Instead, it’s all about the changing electric fields. Here are some key characteristics to help you understand this concept better:

• It’s Like an Invisible Current: Displacement current occurs in spaces where there is a changing electric field, like between the plates of a capacitor when it’s charging or discharging. There’s no actual movement of charges, but the effect is similar to a real current.
• Measured in Amperes: Just like the current you measure with a multimeter, displacement current is also measured in Amperes (A). This means it has the same “size” or “amount” as a current made of moving charges.
• Creates Magnetic Fields: One of the coolest things about displacement current is that it can create magnetic fields. This is similar to how a wire carrying an electric current creates a magnetic field around it. So, even though it’s “invisible,” it still has real effects in the physical world.
• Vector Quantity: Displacement current is a vector quantity, which means it has both magnitude and direction. This is important because it tells us not just how strong the current is, but also in which direction the electric field is changing.
• Depends on Time: The strength of the displacement current depends on how quickly the electric field changes over time. If the field changes rapidly, the displacement current is strong; if it changes slowly, the current is weak.
• Consistent with Conduction Current: When you add up the displacement current and the conduction current (the one with real charges moving), the total current remains constant along a closed path. This is a key principle that helps make sense of how electric and magnetic fields interact.
• Triggered by Changing Electric Fields: Lastly, what triggers the displacement current? It’s the rate at which the electric field changes. This is why it’s so important in capacitors, where the electric field changes as they charge and discharge.

Application of Displacement Current

The concept of displacement current plays a crucial role in our understanding of electromagnetism and has several practical applications:

1. Wireless Communication: Displacement current is fundamental to the operation of antennas used in wireless communication. When an antenna transmits, it creates a changing electric field, which in turn generates a displacement current. This displacement current produces electromagnetic waves that carry signals across distances.
2. Capacitors in Circuits: In electronic circuits, capacitors are used to block direct current while allowing alternating current to pass. The displacement current explains why capacitors can pass alternating current—because the changing electric field between the plates of the capacitor generates a displacement current that can create a magnetic field and propagate the signal.
3. Power Factor Correction: The displacement current is responsible for the leading nature of the current in capacitors. This means that in AC circuits, the current can lead to the voltage. This property is used to improve the power factor, which is a measure of how effectively electrical power is converted into useful work output. By adjusting the power factor, we can make electrical systems more efficient.
4. Electromagnetic Field Theory: The concept of displacement current is essential in Maxwell’s equations, which are the foundation of electromagnetic field theory. These equations describe how electric and magnetic fields are generated and interact with each other, leading to the prediction and understanding of electromagnetic waves.
5. Radar and Imaging Technology: Displacement current is also important in radar technology, where electromagnetic waves are used to detect the position, velocity, or other characteristics of distant objects. Similarly, in imaging technology, varying electric fields are used to create images of the inside of objects or bodies without invasive procedures.

The displacement current is not just a theoretical concept but has real-world applications that affect various technologies we use every day. From the smartphone in your hand to the medical equipment in hospitals, displacement current helps make modern life possible.

Solved Examples

Example 1: A parallel plate capacitor with a capacitance of (2 µF) is connected to a battery and charged by a current of (10 mA). Calculate the displacement current between the plates of the capacitor.

Solution: The displacement current (I_d) is equal to the conduction current (I) charging the capacitor.

Given; Conduction current (I = 10 mA = 10 \times 10^-3 A)

Since the displacement current in a capacitor is equal to the conduction current during charging:

\(\displaystyle I_d = I = 10 \, \text{mA} \)

Therefore, the displacement current is (10 mA).

Example 2: A parallel plate capacitor with a plate area of (0.02m²) and plate separation of (1 mm) is connected to an AC source providing a current \(\displaystyle I(t) = 5 \cos(1000t) \, \text{mA}\). Calculate the magnetic field at a distance of (5 cm) from the axis of the plates.

Solution: The magnetic field (B) around a displacement current is given by:

\(\displaystyle B(2\pi r) = \mu_0 I_d \)

Given:

• Displacement current \(\displaystyle I_d = 5 \cos(1000t) \, \text{mA} = 5 \times 10^{-3} \cos(1000t) \, \text{A}\)
• Distance (r = 5 cm = 0.05m)
• Permeability of free space \(\displaystyle\mu_0 = 4\pi \times 10^{-7} \, \text{H/m}\)

\(\displaystyle B(2\pi \times 0.05) = 4\pi \times 10^{-7} \times 5 \times 10^{-3} \cos(1000t) \)

\(\displaystyle B(0.1\pi) = 20\pi \times 10^{-10} \cos(1000t) \)

\(\displaystyle B = \frac{20\pi \times 10^{-10} \cos(1000t)}{0.1\pi} \)

\(\displaystyle B = 2 \times 10^{-9} \cos(1000t) \)

Therefore, the magnetic field at a distance of (5 cm) from the axis of the plates is \(\displaystyle 2 \times 10^{-9} \cos(1000t) \, \text{T}\).

Example 3: An electric field between the plates of a parallel plate capacitor is given by \(\displaystyle E(t) = 500 \sin(2000t) \, \text{V/m}\). The area of each plate is (0.01m²) and the plate separation is (2 mm). Calculate the displacement current density.

Solution: The displacement current density (J_d) is given by:

\(\displaystyle J_d = \epsilon_0 \frac{dE}{dt} \)

Given:

• Electric field \(\displaystyle E(t) = 500 \sin(2000t) \, \text{V/m}\)
• Permittivity of free space \(\displaystyle\epsilon_0 = 8.854 \times 10^{-12} \, \text{F/m}\)

First, find the time derivative of the electric field (E):

\(\displaystyle \frac{dE}{dt} = 500 \cdot 2000 \cos(2000t)\)

\(\displaystyle\frac{dE}{dt} = 1 \times 10^6 \cos(2000t) \)

Now, calculate (J_d):

\(\displaystyle J_d = 8.854 \times 10^{-12} \times 1 \times 10^6 \cos(2000t) \)

\(\displaystyle J_d = 8.854 \times 10^{-6} \cos(2000t) \)

Therefore, the displacement current density is \(\displaystyle 8.854 \times 10^{-6} \cos(2000t) \, \text{A/m}^2\).

Example 4: A capacitor with a dielectric of the relative permittivity \(\displaystyle\epsilon_r = 4\) and plate area (0.1 m²) is subjected to an electric field \(\displaystyle E(t) = 300 \cos(1000t) \, \text{V/m}\). Calculate the displacement current between the plates.

Solution: The displacement current (I_d) is given by:

\(\displaystyle I_d = \epsilon_0 \epsilon_r A \frac{dE}{dt} \)

Given:

• Electric field \(\displaystyle E(t) = 300 \cos(1000t) \, \text{V/m}\)
• Area (A = 0.1m²)
• Relative permittivity \(\displaystyle\epsilon_r = 4\)
• Permittivity of free space \(\displaystyle\epsilon_0 = 8.854 \times 10^{-12} \, \text{F/m}\)

First, find the time derivative of the electric field (E):

\(\displaystyle \frac{dE}{dt} = 300 \cdot (-1000) \sin(1000t) \)

\(\displaystyle \frac{dE}{dt} = -300000 \sin(1000t) \)

Now, calculate (I_d):

\(\displaystyle I_d = 8.854 \times 10^{-12} \times 4 \times 0.1 \times (-300000) \sin(1000t) \)

\(\displaystyle I_d = -1.06248 \times 10^{-7} \sin(1000t) \)

Therefore, the displacement current is approximately \(\displaystyle -1.06248 \times 10^{-7} \sin(1000t) \, \text{A}\).

Example 5: The electric field between the plates of a capacitor is given by \(\displaystyle E(t) = 600 \cos(3000t) \, \text{V/m}\). The area of each plate is (0.2 m²) and the plate separation is (0.5 mm). Calculate the displacement current between the plates.

Solution: The displacement current (I_d) is given by:

\(\displaystyle I_d = \epsilon_0 A \frac{dE}{dt} \)

Given:

• Electric field \(\displaystyle E(t) = 600 \cos(3000t) \, \text{V/m}\)
• Area (A = 0.2 m²)
• Permittivity of free space \(\displaystyle\epsilon_0 = 8.854 \times 10^{-12} \, \text{F/m}\)

First, find the time derivative of the electric field (E):

\(\displaystyle \frac{dE}{dt} = 600 \cdot (-3000) \sin(3000t) \)

\(\displaystyle \frac{dE}{dt} = -1800000 \sin(3000t) \)

Now, calculate (I_d):

\(\displaystyle I_d = 8.854 \times 10^{-12} \times 0.2 \times (-1800000) \sin(3000t) \)

\(\displaystyle I_d = -3.18096 \times 10^{-6} \sin(3000t) \)

Therefore, the displacement current is approximately \(\displaystyle -3.18096 \times 10^{-6} \sin(3000t) \, \text{A}\).

Example 6: In an electromagnetic wave, the electric field varies as \(\displaystyle E(t) = 400 \sin(2 \pi \times 10^6 t) \, \text{V/m}\). Calculate the corresponding displacement current density if the wave propagates in a vacuum.

Solution: The displacement current density (J_d) is given by:

\(\displaystyle J_d = \epsilon_0 \frac{dE}{dt} \)

Given:

• Electric field \(\displaystyle E(t) = 400 \sin(2 \pi \times 10^6 t) \, \text{V/m}\)
• Permittivity of free space \(\displaystyle \epsilon_0 = 8.854 \times 10^{-12} \, \text{F/m}\)

First, find the time derivative of the electric field (E):

\(\displaystyle \frac{dE}{dt} = 400 \cdot 2 \pi \times 10^6 \cos(2 \pi \times 10^6 t) \)

\(\displaystyle \frac{dE}{dt} = 8 \pi \times 10^8 \cos(2 \pi \times 10^6 t) \)

Now, calculate (J_d):

\(\displaystyle J_d = 8.854 \times 10^{-12} \times 8 \pi \times 10^8 \cos(2 \pi \times 10^6 t) \)

\(\displaystyle J_d = 222.08 \cos(2 \pi \times 10^6 t) \, \text{A/m}^2\)

Therefore, the displacement current density is \(\displaystyle 222.08 \cos(2 \pi \times 10^6 t) \, \text{A/m}^2\).

FAQs