The phenomenon of eddy currents has been around since the beginning of electromagnetism, but it wasn’t until the 19th century that it was observed and understood. The story begins with François Arago, who in 1824 noticed something peculiar. He observed that a rotating copper disk could cause a compass needle to move. This was the first hint at the existence of eddy currents, although Arago didn’t fully understand the mechanism behind it.
It took about 30 more years for the full picture to come into focus. Enter Léon Foucault, a brilliant French physicist. In 1855, Foucault conducted experiments that led to the discovery of these mysterious currents. He used a copper disk, similar to Arago’s, and showed that when it was rotated in the presence of a magnetic field, it heated up due to currents flowing in circles within the disk. These currents were induced by the changing magnetic field, as described by Faraday’s law of induction.
Foucault’s experiments were groundbreaking because they demonstrated how a changing magnetic field could induce currents in a conductor without any direct electrical connection. This was a significant step forward in the understanding of electromagnetism.
The term “eddy current” comes from the analogy of water in a stream hitting an obstacle and creating whirlpools or “eddies.” Similarly, the magnetic field creates whirlpools of current in the conductor. These currents were initially called Foucault’s currents in honor of their discoverer, but over time, the term “eddy current” became more widely used.
The understanding of eddy currents was further developed by the work of other scientists, including James Clerk Maxwell, who incorporated them into his famous equations that describe all of electromagnetism.
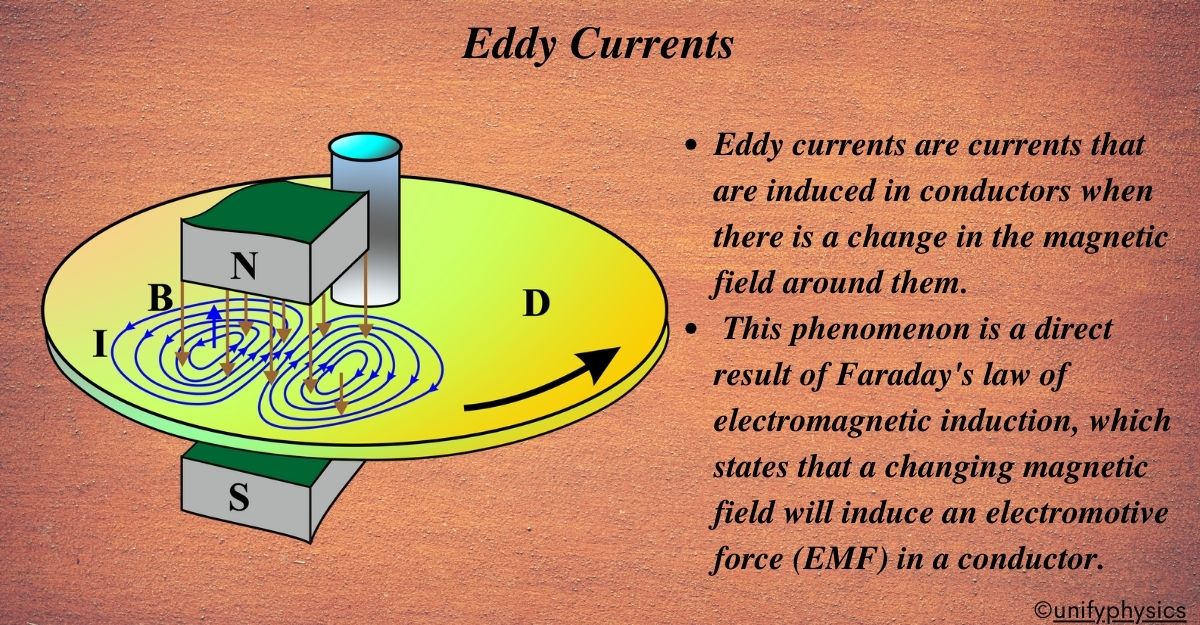
Formation of Eddy Currents
What are Eddy Currents?
“Eddy currents are loops of electrical current induced within conductors when they are exposed to a changing magnetic field. These currents are named ‘eddy’ because they often form swirling patterns similar to eddies in water.”
According to Faraday’s law of induction, eddy currents are generated, which states that a changing magnetic field within a conductor induces an electromotive force (EMF). This induced EMF causes currents to flow in the conductor.
Eddy currents are currents induced in conductors when there is a change in the magnetic field around them. This phenomenon directly results from Faraday’s law of electromagnetic induction, which states that a changing magnetic field will induce an electromotive force (EMF) in a conductor.
Changing Magnetic Field
When a conductor, such as a piece of metal, is placed in a magnetic field that is changing in time—either because the strength of the magnetic field is changing or because the conductor is moving through it—an EMF is induced in the conductor.
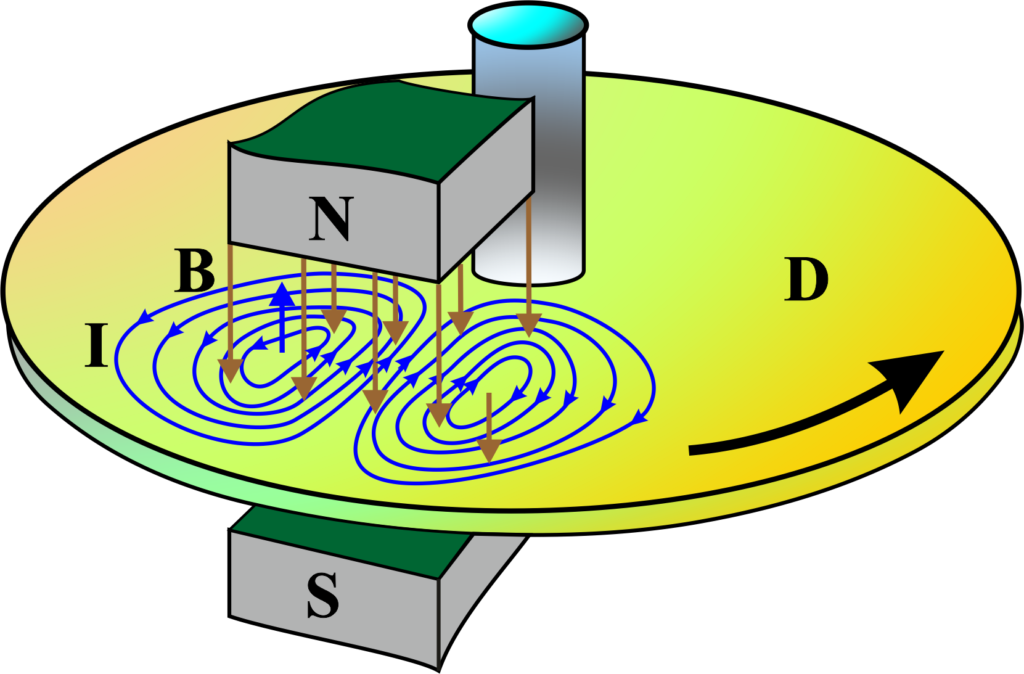
This induced EMF causes currents to flow within the conductor. However, unlike in a coil where the current follows a single path, these currents swirl around in the conductor, forming closed loops. These loops of current are what we call eddy currents.
According to Lenz’s law, the direction of the induced eddy currents will be such that they create their magnetic field, which opposes the change in the original magnetic field that induced them. This is a manifestation of the conservation of energy principle.
Factors Affecting Eddy Currents
The magnitude of the eddy currents depends on several factors:
- The rate at which the magnetic field changes.
- The electrical conductivity of the conductor.
- The thickness and geometry of the conductor.
- The presence of any gaps or slits in the conductor, which can disrupt the flow of eddy currents.
Eddy currents can be visualized as swirling patterns of current, similar to eddies in water, hence the name. They flow in closed loops within the conductor, in planes perpendicular to the magnetic field. While eddy currents can cause energy losses in the form of heat (which is undesirable in some applications like transformers), they are also harnessed for useful purposes. For example, in induction heating and braking systems, the heat generated by eddy currents is used to heat objects or slow down moving parts.
Characteristics of Eddy Currents
- Eddy currents are circular currents induced in conductive materials when they are exposed to a changing magnetic field. These materials can include metals like copper, aluminum, and iron.
- Eddy currents flow in closed loops or circles within the material. The direction of these currents depends on the direction of the changing magnetic field and obeys Lenz’s Law, which states that the induced current creates a magnetic field that opposes the change in the original magnetic field.
- The strength of eddy currents is directly proportional to the rate of change of the magnetic field inducing them. A faster-changing magnetic field will induce stronger eddy currents, while a slower-changing field will induce weaker currents.
- Eddy currents encounter resistance as they flow through the conductive material, resulting in the conversion of electrical energy into heat energy. This phenomenon, known as Joule heating, can lead to the material heating up if not properly controlled.
- Eddy currents produce a damping effect on the motion of objects moving through a magnetic field. For example, in eddy current brakes used in trains, the interaction between the eddy currents induced in the brake discs and the magnetic field slows down the motion of the train by converting kinetic energy into heat energy.
- Eddy currents are utilized in non-destructive testing methods to detect defects or inconsistencies in conductive materials. By analyzing changes in the eddy currents induced in the material, flaws such as cracks or voids can be identified without damaging the material.
Lenz’s Law and Eddy Currents
Lenz’s Law and eddy currents are fundamentally connected through the principles of electromagnetic induction.
Lenz’s Law: Lenz’s Law states that the direction of an induced current in a conductor due to a changing magnetic field is such that it opposes the change that produced it. This law is a manifestation of the conservation of energy, ensuring that the induced current cannot create energy from nothing.
Eddy Currents: Eddy currents are loops of induced current that form within conductors when they are exposed to a changing magnetic field. These currents can flow in closed loops and create their magnetic fields.
The connection between Lenz’s Law and eddy currents lies in the fact that the magnetic fields created by eddy currents always act to oppose the change in the original magnetic field that induced them. For example, if a metal plate moves through a magnetic field, eddy currents are induced in the plate. According to Lenz’s Law, the magnetic field of these eddy currents will oppose the motion of the plate, effectively resisting the change in magnetic flux.
This opposition can have practical implications. For instance, in induction heating, the resistance of the metal to the eddy currents generates heat. In magnetic braking systems, the opposing force from the eddy currents is used to slow down moving objects, such as trains.
To visualize this, imagine dropping a strong magnet through a copper tube. As the magnet falls, it induces eddy currents in the walls of the tube. These currents produce magnetic fields that oppose the magnet’s motion, slowing its descent. This is a direct consequence of Lenz’s Law, as the induced magnetic fields work to counteract the change in magnetic flux caused by the falling magnet.
Effects of Eddy Currents
Eddy currents are currents induced in conductors when they are exposed to a changing magnetic field. These currents can have various effects, both beneficial and detrimental, depending on the application.
- Heating Effect: Eddy currents can generate heat due to the electrical resistance of the material in which they flow. This heating effect is utilized in induction heating applications, such as cooktops and industrial furnaces, where the heat generated by eddy currents is used to cook food or melt metals.
- Magnetic Braking: In magnetic braking systems, such as those used in some trains and amusement park rides, eddy currents are used to produce a braking force. When a conductor moves through a magnetic field, eddy currents are induced, and the magnetic field created by these currents opposes the motion, slowing down the object.
- Energy Losses: In electrical systems like transformers and motors, eddy currents can lead to energy losses. These losses are undesirable as they reduce the efficiency of the device by converting useful energy into heat. To minimize these losses, the cores of such devices are often made from laminated steel sheets, which restrict the flow of eddy currents.
- Eddy Current Testing: Eddy currents are used in non-destructive testing methods to detect flaws in metal structures. Changes in the flow of eddy currents can indicate the presence of cracks, corrosion, or other defects.
- Electromagnetic Damping: In instruments like galvanometers, eddy currents are used to provide damping. The eddy currents induced in a moving metal part create a magnetic field that opposes the motion, quickly bringing the moving part to rest without oscillation.
- Power Meters: In electric power meters, eddy currents are used to rotate a metal disc. The speed of rotation is proportional to the power consumption, allowing the meter to measure the amount of electrical energy used.
These are some of the key effects of eddy currents.
Reducing Eddy Currents
To minimize energy losses due to eddy currents in electrical devices, the cores of transformers and motors are often made from laminated sheets of metal. This construction increases the resistance to the flow of eddy currents and thus reduces their magnitude.
Laminated Cores: One of the most common methods to reduce eddy currents is to use laminated cores in electrical machines. Laminating the core means stacking thin sheets of magnetic material, separated by an insulating layer, such as varnish. This increases the resistance of the path along which eddy currents can flow, thus reducing their magnitude.
Slots and Holes: Adding slots or holes in the conductor can disrupt the path of eddy currents, preventing them from forming large loops. This technique is often used in the design of induction motors.
Use of Non-Magnetic Materials: Since eddy currents are induced in magnetic materials, using non-magnetic materials where possible can help reduce the formation of eddy currents. However, this is not always practical, as magnetic materials are often required for their desirable magnetic properties.
High Resistivity Materials: Choosing materials with high electrical resistivity for the construction of the core can also reduce eddy currents. High resistivity materials impede the flow of current, thus limiting the formation of eddy currents.
Proper Design: Careful design of electrical devices can minimize the effects of eddy currents. For example, the shape and size of the core, the thickness of the laminations, and the overall configuration of the device can be optimized to reduce eddy currents.
Explanation of Braking using Eddy Currents
To understand eddy current brakes, we need to start with the basics of electromagnetic induction. When a conductor moves through a magnetic field, or when a magnetic field moves around a conductor, it induces a voltage across the conductor. This is known as Faraday’s Law of Electromagnetic Induction. If the conductor is part of a closed circuit, this induced voltage will cause a current to flow. These currents are called eddy currents because they tend to circulate in loops within the conductor, much like eddies in a stream.
Now, according to Lenz’s Law, the direction of these induced eddy currents will be such that they create their own magnetic field which opposes the change in the magnetic field that produced them. This opposition creates a force, and it’s this force that is used in eddy current brakes.
The Braking Process: Imagine you have a metal wheel spinning near a magnet. As the wheel spins, it cuts through the magnetic field, and eddy currents are induced in the wheel. These eddy currents generate their own magnetic field that opposes the original magnetic field of the magnet. The interaction between these magnetic fields produces a force that opposes the motion of the wheel, thus slowing it down.
This is how eddy current brakes work. They convert the kinetic energy of the moving object into heat energy through the process of electromagnetic induction. The beauty of this system is that it’s a non-contact form of braking. There’s no friction involved, so there’s less wear and tear, making it a very efficient form of braking.
Eddy current brakes are used in various applications, from amusement park rides to high-speed trains. For example, some roller coasters use eddy current brakes to provide a smooth and controlled stop. High-speed trains, like the Japanese Shinkansen, also use this technology to ensure quick and reliable braking without the downsides of friction-based systems.
Advantages of Eddy Current Brakes:
- No physical contact means less maintenance and longer-lasting components.
- Smooth operation as the braking force is evenly distributed across the braking surface.
- Adjustable braking force by changing the strength of the magnetic field or the electrical conductivity of the wheel.
So, eddy current brakes are a clever use of electromagnetic principles to achieve efficient and reliable braking without the need for physical contact.
Also Read: Lenz’s Law
Applications of Eddy Currents
- Magnetic Braking: Eddy currents slow down trains and roller coasters without physical contact, ensuring smooth braking.
- Induction Heating: Eddy currents heat metal quickly and efficiently in industrial processes like welding and metal forging.
- Non-Destructive Testing: Eddy currents detect defects in metals without damaging them, aiding in quality control.
- Metal Sorting: Eddy currents separate different metals in recycling plants based on their conductivity, enhancing recycling efficiency.
- Vibration Damping: Eddy currents reduce mechanical vibrations in devices like dynamic dampers, improving stability and performance.
Example
Example 1:A circular metallic disk rotates at a constant angular velocity about an axis perpendicular to its plane. When it is rotated in a magnetic field, eddy currents are induced in it. Which of the following statements is correct regarding the induced currents?
(a) The induced currents increase with an increase in the angular velocity.
(b) The induced currents decrease with an increase in the angular velocity.
(c) The induced currents are independent of the angular velocity.
(d) The induced currents reverse direction with an increase in the angular velocity.
Solution:(c) The induced currents are independent of the angular velocity. Eddy currents depend on the rate of change of magnetic flux, which is constant in this scenario as the angular velocity remains constant.
Example 2: A metallic disc of radius 0.1 m rotates at 1000 rpm in a plane normal to the direction of a uniform magnetic field of induction 0.1 T. The maximum emf induced between the rim and the center of the disc is close to:
(a) 1 mV
(b) 10 mV
(c) 100 mV
(d) 1 V
Solution: (b) 10 mV. We can use the formula for the motional EMF induced in a rotating disc:
\(\displaystyle \varepsilon = \frac{B \cdot A \cdot \omega}{2} \)
where, B is the magnetic field (0.1 T), A is the area of the disc \(\displaystyle\pi \times (0.1)^2 m²\), and ω is the angular velocity \(\displaystyle\frac{1000}{60} rad/s\).
Plugging in the values, we get:
\(\displaystyle \varepsilon = \frac{0.1 \, \text{T} \times \pi \times (0.1)^2 \, \text{m²} \times \frac{1000}{60} \, \text{rad/s}}{2} \)
\(\displaystyle \varepsilon = \frac{0.1 \times 0.01 \times \pi \times \frac{1000}{60} \, \text{V}}{2} \)
\(\displaystyle\varepsilon \approx 0.1 \, \text{V} \)
Hence, the maximum emf induced is close to 10 mV (option b).
Example 3: A metallic rod is dropped from a height h above a horizontal surface. If the rod experiences a retarding force due to eddy currents induced in it, the time taken by the rod to come to rest is proportional to:
(a) \(\displaystyle \sqrt{h}\)
(b) \(\displaystyle h^{3/2} \)
(c) h2
(d) \(\displaystyle \frac{1}{h}\)
Solution: (a) \(\displaystyle\sqrt{h} \). The time taken for the rod to come to rest is proportional to the square root of the distance it falls, \(\displaystyle\sqrt{h}\).
When the metallic rod falls, it experiences a retarding force due to the eddy currents induced in it. This force opposes the motion of the rod and eventually brings it to rest. The time taken for the rod to come to rest can be found using principles of kinematics. The deceleration due to the retarding force is constant, as the gravitational force acting on the rod is constant.
The distance fallen by the rod is proportional to the square of the time, ( t2), according to the equations of motion. Hence, the time taken for the rod to come to rest is proportional to \(\displaystyle \sqrt{h}\).
This relationship arises because the distance fallen by an object under constant acceleration is proportional to the square of the time taken. Since the retarding force due to eddy currents provides a constant deceleration, the time taken for the rod to come to rest is proportional to the square root of the height from which it is dropped, \(\displaystyle\sqrt{h} \). Therefore, the correct option is (a) \(\displaystyle \sqrt{h} \).
Example 4: A solid metallic sphere of radius R and conductivity σ is dropped from a height h above a region of uniform magnetic field B, directed perpendicular to the plane of the paper. If the sphere acquires a terminal velocity vt on account of eddy currents induced in it, the expression for vt is:
(a) \(\displaystyle\sqrt{\frac{2gh}{\sigma B^2 R^2}} \)
(b) \(\displaystyle\sqrt{\frac{2gh}{\sigma B^2 R}}\)
(c)\(\displaystyle\sqrt{\frac{2gh}{\sigma B R^2}}\)
(d) \(\displaystyle\sqrt{\frac{2gh}{\sigma B R}}\)
Solution: (c) \(\displaystyle\sqrt{\frac{2gh}{\sigma B R^2}}\). The terminal velocity vt can be derived from the force balance equation between the gravitational force and the force due to eddy currents.
Example 5: A metallic ring of radius R and resistance R is falling vertically down in a region of uniform magnetic field B. The electric field induced in the ring is:
(a) \(\displaystyle\frac{m^2}{2} \)
(b)\(\displaystyle\frac{m}{2}\)
(c) \(\displaystyle\frac{m}{4}\)
(d) \(\displaystyle\frac{m^2}{4}\)
Solution: (b) \(\displaystyle\frac{m}{2} \). The induced electric field in the ring is given by Faraday’s law of electromagnetic induction,
\(\displaystyle\varepsilon = -\frac{d\Phi}{dt}\),
The magnetic flux Φ through the ring is proportional to the area of the ring A that is intersected by the magnetic field. As the ring falls, this area changes at a rate equal to the velocity of the ring v, which is given as (m) mass of the ring in the problem.
As the ring falls vertically down, the magnetic flux through the ring changes. The magnetic flux Φ is given by:
\(\displaystyle\Phi = B \cdot A \)
Where A is the area of the ring that is perpendicular to the magnetic field. Since the ring is falling vertically down, the area of the ring that is perpendicular to the magnetic field changes with time. Let’s denote this area as A(t) . Now, the induced EMF is:
\(\displaystyle \varepsilon = -\frac{d\Phi}{dt} = -\frac{d}{dt} (B \cdot A) \)
Since the magnetic field B is uniform and perpendicular to the plane of the ring, the change in area A with time \(\displaystyle\frac{dA}{dt} \) is equal to the velocity of the ring v = m, where m is the mass of the ring. Thus, we have:
\(\displaystyle \frac{dA}{dt} = m \)
Substituting this into the equation for induced EMF, we get:
\(\displaystyle\varepsilon = -\frac{d}{dt} (B \cdot A) = -B \cdot \frac{dA}{dt} = -B \cdot m \)
Now, the induced electric field E in the ring is given by dividing the induced EMF by the circumference of the ring \(\displaystyle 2\pi R\) :
\(\displaystyle E = \frac{\varepsilon}{2\pi R} = \frac{-B \cdot m}{2\pi R} \)
So, the induced electric field in the ring is \(\displaystyle\frac{-B \cdot m}{2\pi R} \), which is equivalent to option (b) \(\displaystyle \frac{m}{2}\). Therefore, the correct answer is option (b).
FAQs
What are eddy currents?
Eddy currents are loops of electric current that are induced within conductors when they are exposed to a changing magnetic field. These currents circulate in the plane perpendicular to the magnetic field and can cause significant power loss due to their resistive heating effect.
How are eddy currents generated?
Eddy currents are generated when a conductor experiences a change in magnetic flux. This change induces a circulating flow of electrons within the conductor, forming closed loops of current known as eddy currents.
What are some common applications of eddy currents?
Eddy currents are used in various applications, including induction heating, metal detectors, and electromagnetic braking systems in trains. They are also employed in non-destructive testing techniques to detect cracks and flaws in metal structures.
What are the effects of eddy currents in transformers and electric motors?
In transformers and electric motors, eddy currents can cause undesirable power losses and heating within the core materials. To minimize these effects, core materials are often laminated, which restricts the flow of eddy currents and reduces energy losses.
How do eddy current brakes work?
Eddy current brakes work by moving a conductor through a magnetic field. The change in magnetic flux induces eddy currents in the conductor, which generate opposing magnetic fields. These opposing fields create a resistive force that slows down the motion, providing a braking effect without physical contact.
What measures can be taken to reduce the negative effects of eddy currents?
To reduce the negative effects of eddy currents, materials with high electrical resistance and low magnetic permeability are used. Additionally, components such as transformer cores and motor armatures are often laminated, which restricts the flow of eddy currents and minimizes energy loss.
How do eddy currents affect the efficiency of electrical devices?
Eddy currents can decrease the efficiency of electrical devices by causing resistive heating and energy loss. This inefficiency is especially significant in devices like transformers, motors, and generators. By using laminated cores and optimizing the material properties, the impact of eddy currents can be mitigated, improving the overall efficiency of these devices.