The concept of elasticity has been around for centuries, but it was during the scientific revolution of the 17th and 18th centuries that significant progress was made.
People have always been aware of elastic materials. For instance, the use of bows in archery demonstrated an understanding of how some materials can return to their original shape after being deformed.
The real scientific study of elasticity began with Robert Hooke (1635-1703), an English scientist. In 1676, he stated what we now call Hooke’s Law: This law describes how the distance a spring stretches (extension) is proportional to the force applied to it. Hooke’s work was the foundation for understanding the elastic behavior of materials.
Later, Thomas Young (1773-1829), an English polymath, contributed to the field by defining the modulus of elasticity. This is a measure of the stiffness of a material, which is still a key concept in materials science and engineering today.
The French mathematician Augustin-Louis Cauchy (1789-1857) further developed the theory of elasticity. He studied the stress and strain in materials, laying the groundwork for the complex mathematics that describes elastic materials.
James Clerk Maxwell (1831-1879), a Scottish physicist, is known for his work on electromagnetism, but he also made contributions to the theory of elasticity. He developed equations that describe the behavior of elastic fields in materials.
In the 20th century, the field of materials science expanded rapidly. With the advent of new materials and technologies, the study of elasticity has become even more important. Today, we use the principles of elasticity to design everything from skyscrapers to smartphone screens.
What is Elasticity?
Elasticity is a material property that returns to its original shape and size after the forces causing deformation are removed. It’s like a rubber band snapping back after being stretched.
Imagine you have a spring or a rubber band. When you pull on it, it stretches, right? Now, when you let go, it goes back to its original shape. That’s elasticity in action!
In physics, elasticity is the ability of a material to return to its original shape and size after the forces causing it to change are removed. It’s like a memory that the material has, always remembering and returning to its original form.
Here’s a simple formula that relates to elasticity, known as Hooke’s Law:
\(\displaystyle F = -kx \)
- (F) is the force applied to the material,
- (k) is the spring constant (a measure of the stiffness of the spring),
- (x) is the displacement from the original position.
The negative sign indicates that the force exerted by the spring is in the opposite direction of the displacement.
There’s a limit to how much you can stretch something before it stops being elastic. This is called the elastic limit. If you stretch a material beyond this point, it won’t return to its original shape, and it might even break. This is when we start talking about plasticity, but that will be discussed later.
Elasticity is super important in everyday life. It’s what makes our bridges flex under the weight of cars without breaking, allows skyscrapers to sway in the wind, and even lets us bounce on a trampoline.
So, in short, elasticity is all about how materials can bounce back to their original form after being stretched, compressed, or bent. It’s a fundamental property that engineers and scientists consider when designing and choosing materials for all sorts of applications.
What is Deformation?
Deformation refers to the change in shape or size of an object due to an applied force. If you press a sponge, it deforms, and when you release it, it goes back to its original shape if the deformation is within the elastic limit.
Imagine you have a favorite rubber band. In physics, deformation is simply what happens to the rubber band when you stretch it, squish it, or twist it out of shape. It’s any change in the size or shape of an object.
The rubber band has a natural resting shape. When you apply a force, like pulling it, the internal arrangement of particles (atoms) in the band gets disrupted. This disrupts the shape and size of the whole object, which is the deformation.
Stress and Strain: To describe deformation, we use two key terms:
Stress: It’s the force applied over a certain area. Imagine pressing your thumb into a piece of clay; the force your thumb exerts over the area of contact is stress.
Strain: It’s the measure of how much the object has deformed. If you stretch a rubber band to twice its length, the strain is the change in length compared to the original length.
Deformation can be temporary or permanent. If you let go of the stretched rubber band, it might snap back to its original shape (elastic deformation). But if you pull too hard, it might stay stretched out (plastic deformation).
Deformation is all about how forces can change the shape and size of objects, and how those objects respond to those changes. It’s a fundamental concept in understanding how materials behave under stress.
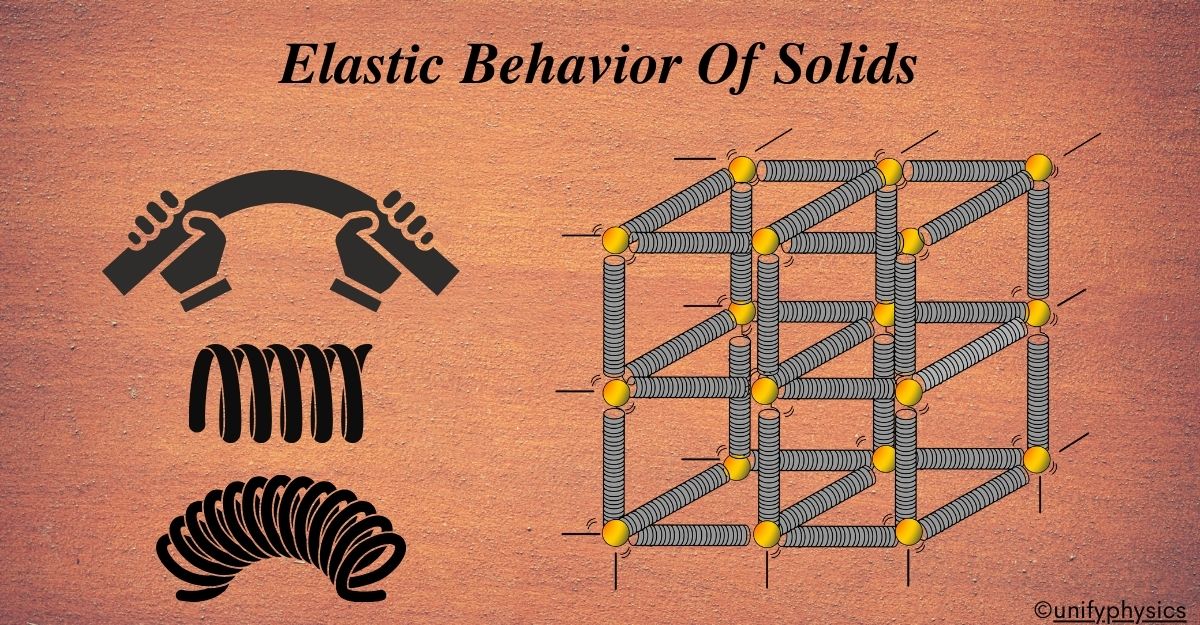
Elastic Behaviour of Solids
Solids show elastic behavior when the forces acting on them are removed, and they return to their original state. This happens because the atoms or molecules in a solid are displaced but return to their equilibrium positions due to interatomic forces.
When you stretch a rubber band by hand, you’ll notice that it elongates, right? But here’s the interesting part: once you release the force (stop stretching), the rubber band returns to its original shape. This ability of the rubber band to regain its original shape after the force is removed is what we call elastic behavior.
Think of the rubber band as a group of tiny, interconnected springs. When you stretch it, you’re pulling those springs apart. But because of the molecular structure of rubber, those “springs” want to pull back together. That’s why when you let go, the rubber band snaps back to its original form.
This ability to stretch and return to its original shape is what makes rubber bands useful in everyday life, like holding things together or making simple machines work. It’s also a classic example of elasticity in solids. So, elastic behavior essentially refers to the ability of a material to deform when a force is applied and then return to its original shape once the force is removed.
Another example, Imagine you have a model made of a bunch of small balls (representing atoms or molecules) connected by springs (representing the bonds between them). When the model is in its relaxed state, the balls are at their equilibrium positions, and the springs are not stretched or compressed.
Now, if you apply a force to the model, let’s say by pulling on one end, what happens? The springs start to stretch. As you continue to apply force, the springs elongate further, causing the balls to move away from their equilibrium positions.
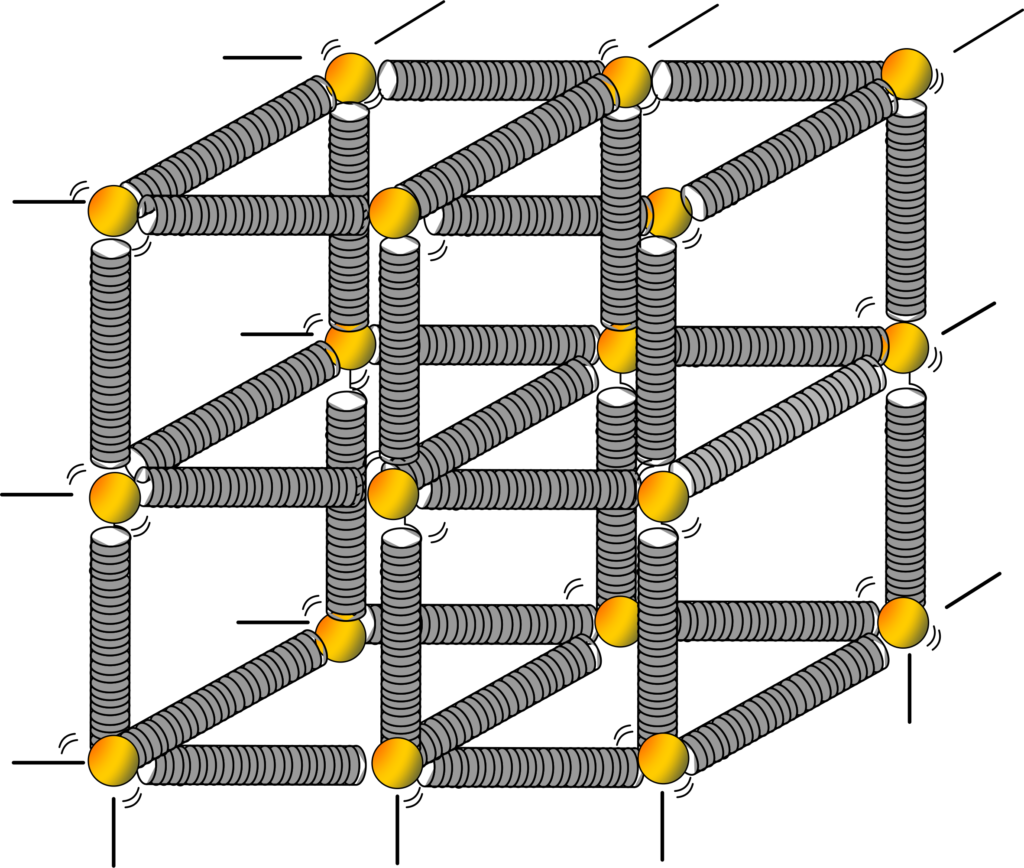
However, here’s the key point: the springs are elastic, meaning they tend to return to their original length when the force is removed. So, as long as the force you apply doesn’t exceed the elastic limit of the material, the springs will bounce back to their original length once you release the force.
This bouncing back is what we call elastic behavior. Just like the springs in our model, real materials like metals, rubber, or even bones exhibit elastic behavior. When a force is applied to them, they deform temporarily, but they return to their original shape and size once the force is removed, as long as the force doesn’t cause permanent damage.
Solids are made up of atoms and molecules that are tightly packed together. These particles are held in place by forces that act like tiny springs. When you apply a force to a solid, you’re essentially stretching or compressing these ‘atomic springs’. If the force is small enough, the ‘springs’ can pull the atoms back to their original positions when the force is removed. This is what we call elastic behavior.
Elastic limit: Every solid has an elastic limit. This is the maximum extent to which you can deform it without causing a permanent change. It’s like stretching a rubber band too far—it won’t go back to its original size.
Imagine you’re playing with a stretchy toy. You can pull it, twist it, and it’ll snap right back to its original shape. But if you pull too hard, it stays stretched and won’t return to how it was before. That point where it stops being able to return to its original shape is what we call the elastic limit.
In physics terms, the elastic limit is the maximum amount of stress (force per unit area) that a material can withstand while still being able to return to its original shape after the force is removed. It’s like the ultimate test of a material’s flexibility.
- Stress: It’s the force you apply divided by the area over which you apply it.
- Strain: It’s the change in shape or size of the material due to the applied stress.
- Elastic Behavior: It’s when the material can recover its original shape after the stress is removed.
Knowing the elastic limit is super important for engineers and designers. It helps them choose the right materials for buildings, bridges, and even everyday items like glasses and electronics. They need materials that won’t permanently deform under the stresses of everyday use.
So, the elastic limit is like the superhero’s limit in a material. It tells us how much the material can handle before it gives up and changes for good. And just like superheroes, different materials have different limits based on their ‘superpowers’ or properties.
In an ideal world, a perfectly elastic material would return to its original shape no matter how many times it’s deformed, as long as it’s within the elastic limit. In the real world, materials will eventually wear out or even break if you keep deforming them. For example, if you repeatedly bend a paperclip back and forth, it will eventually snap. This is because real-world materials also experience plastic deformation, where the changes become permanent. Engineers use materials with high elasticity for parts that need to flex without breaking, like the springs in a car’s suspension system.
The elastic behavior of solids refers to their ability to resist permanent changes and return to their original shape after being deformed. It’s a property that allows materials to absorb energy and then release it, much like a spring does when it’s compressed and then allowed to expand.
Examples of Elastic Behavior of Solids
1) Rubber Bands: When you stretch a rubber band, it elongates. Once you release it, it snaps back to its original size and shape. This is a classic example of elasticity—where the material returns to its original form after the deforming force is removed.
2) Springs: Springs found in pens, mattresses, or vehicles demonstrate elasticity. Compress or stretch a spring, and it will return to its initial state after the force is gone. This is why springs are used in shock absorbers; they can absorb energy and then release it, allowing for a smooth ride.
3) Suspension Bridges: The cables of a suspension bridge can handle the weight of the traffic because they are elastic. They stretch slightly under the load and then return to their original tension when the load is gone, maintaining the bridge’s structure.
4) Sports Equipment: The strings of a tennis racket or a badminton racket are elastic. They deform when hitting the ball or shuttlecock and then return to their original state, ready for the next hit.
5) Bouncy Balls: When you drop a bouncy ball, it deforms upon impact with the ground, then it returns to its shape and bounces back up. This is due to the elastic properties of the material it’s made from.
6) Metal Rods and Beams: In construction, metal rods and beams may bend slightly under force but will return to their original shape if the force is within the elastic limit of the material. This property is crucial for the structural integrity of buildings and other constructions.
These examples help illustrate how the elastic behavior of solids is a fundamental concept in physics, playing a critical role in the design and function of many objects and structures we use every day.
Factors Affecting Elasticity
When you think about elasticity, it’s like thinking about what makes a trampoline bouncy or a rubber band stretchy. Several factors can change how elastic a material is, just like how different trampolines have different bounciness. Several factors affect the elasticity of a material, including temperature, material type, and the presence of impurities or defects in the material’s structure.
Here are the main factors:
Temperature: Just like how ice cream melts when it’s hot, materials can become less elastic when they’re heated up. Higher temperatures can make the atoms in a material vibrate more, which can reduce the material’s ability to return to its original shape.
Impurities: Adding something different to a material, like mixing different colors of clay, can change its elasticity. The elasticity can increase or decrease depending on what’s mixed in. It’s like adding sprinkles to dough – it changes how the dough behaves.
Annealing: This is a process where materials are heated and then slowly cooled down. It’s like giving the material a spa treatment to relax it. Annealing can make materials less elastic because it allows the atoms to settle into a more relaxed state.
Material Composition: The type of material matters a lot. Metals, rubber, and plastics all have different levels of elasticity. It’s like comparing a metal spring to a sponge – they respond differently when you press on them.
Structural Defects: If there are flaws or cracks inside a material, it can affect how elastic it is. It’s like having a weak spot on a trampoline – that spot might not be as bouncy as the rest.
Age of the Material: Over time, materials can lose their elasticity. It’s like how an old rubber band might break when you try to stretch it. The material gets tired and can’t bounce back as well.
Mechanical Properties of Solids
When we talk about solids, we’re talking about materials that have a definite shape and size—like a cricket ball, a chocolate bar, or a pencil. But what happens when you apply force to these solids? They exhibit certain behaviors, and these are what we call their mechanical properties. The mechanical properties of solids, like tensile strength and ductility, are influenced by their elastic behavior. These properties determine how a material will deform under various stresses. Let’s look at some of these properties:
Elasticity: This is like the superpower of materials to return to their original shape after being deformed. Think of a spring or a rubber band—when you stretch them and let go, they bounce back to how they were. That’s elasticity in action.
Plasticity: Now, imagine you’re molding clay. You shape it, and it stays in that shape. That’s plasticity—it’s when a material changes shape and doesn’t return to its original form after the force is removed. Plastic materials, like the clay, exhibit this property.
Ductility: Ever seen gold or silver jewelry? These metals can be drawn into thin wires because they’re ductile. Ductility is the property that allows solids to be stretched into long, thin shapes without breaking.
Strength: This is the ability of a material to withstand stress without failing. Some materials, like diamonds, are incredibly strong and can handle a lot of force before they crack or break.
Stress and Strain: When you apply force to a solid, it experiences stress—the force per unit area. The change in the solid’s shape or size due to this force is called strain. It’s like pushing on a door—the stress is your push, and the strain is the door moving.
Hooke’s Law: This law helps us understand how solids behave under stress. It states that the strain in a solid is proportional to the applied stress, within the elastic limit of that solid. Remember, this only applies when the material is behaving elastically.
Moduli of Elasticity: These are measures of a material’s elasticity. They tell us how much a material will deform under stress. There are different types of moduli, like Young’s modulus (for stretching or compressing), shear modulus (for sideways forces), and bulk modulus (for changes in volume).
Physical and Chemical Properties of Solids
The physical and chemical properties of solids, such as density and molecular structure, also play a role in their elasticity. For example, metals are generally more elastic than plastics due to their atomic bonding.
Physical Properties of Solids: When we talk about the physical properties of solids, we’re looking at characteristics that can be observed or measured without changing the substance’s identity. Here are some key physical properties:
- Definite Shape and Volume: Solids have a fixed shape and volume. Unlike liquids or gases, they don’t flow or take the shape of their container.
- Density: Solids usually have a higher density compared to liquids and gases. This means the particles in solids are packed closely together.
- Incompressibility: Solids are hard to compress. Because their particles are so close together, there isn’t much space to squeeze them into.
- Rigidity: Solids are rigid, meaning they resist changes in shape. When you apply force to a solid, it doesn’t easily change its shape unless the force is strong enough.
Chemical Properties of Solids: Chemical properties describe how a substance interacts with other substances, leading to chemical changes. Here are some chemical properties related to solids:
- Reactivity: Some solids react with other substances. For example, iron reacts with oxygen to form rust.
- Flammability: This is a solid’s ability to burn in the presence of oxygen. Wood, for example, is flammable.
- Stability: Chemical stability refers to how likely a solid is to remain unchanged over time. Some solids, like diamonds, are very stable and don’t react easily with other chemicals.
- Electrical and Thermal Conductivity: These properties are related to how well a solid can conduct electricity or heat. Metals are good conductors, while non-metals like rubber are poor conductors.
Understanding these properties helps us predict how a solid will behave in different situations, whether it’s building materials, electronic components, or everyday objects.
What is Plasticity
Plasticity is the opposite of elasticity. It’s the property of a material to undergo permanent deformation without breaking when a force is applied.
Imagine you have a piece of chewing gum. You chew it, and then you stretch it out. No matter what, it won’t go back to the little cube it was before. That’s because it has been plastically deformed.
In physics, plasticity is the property of a material to undergo a permanent change in shape or size when subjected to a force. Once the force is removed, the material does not return to its original shape. This is different from elasticity, where the material would bounce back.
- Elastic Deformation: Like a spring, it returns to its original shape after the force is removed.
- Plastic Deformation: Like chewing gum, it stays stretched and doesn’t go back to its original shape.
It’s all about the atoms in the material. When a force is applied, the atoms move and slide past each other. If the force is strong enough, they can’t slide back into their original positions, leading to a permanent change. When you bend a metal spoon, if you bend it just a little, it will return to its original shape (elasticity). But if you bend it too far, it stays bent (plasticity).
Plasticity is crucial for materials engineering. It helps in designing objects that need to be shaped permanently, like metal car parts or even the braces on your teeth.
So, plasticity is the ability of a material to remember the new shape it’s been forced into, rather than snapping back to its old shape.
Differences Between Elasticity and Plasticity
The main difference is that elasticity is temporary and reversible, while plasticity leads to permanent and irreversible changes in shape.
| Property | Elasticity | Plasticity |
|---|---|---|
| Definition | The ability of a material to return to its original shape after the deforming force is removed. | The ability of a material to undergo permanent deformation without breaking when a force is applied. |
| Deformation | Reversible. The material goes back to its original shape. | Irreversible. The material does not return to its original shape. |
| Behavior Under Stress | Elastic materials will deform under stress but recover their original shape once the stress is removed. | Plastic materials will sustain a permanent change in shape, even after the stress is removed. |
| Stress-Strain Relationship | Within the elastic limit, the stress is directly proportional to the strain. | Beyond the yield point, the material continues to deform at a constant or increasing stress. |
| Energy Absorption | Elastic materials can absorb energy and release it upon returning to their original shape. | Plastic materials may absorb energy during deformation, but they do not release all of it upon unloading. |
| Examples | Rubber bands, springs, and elastic fabrics. | Playdough, putty, and permanently bent metal. |
| Applications | Used in objects that need to return to their original shape, like bungee cords and trampolines. | Used in processes that permanently shape materials, like metal forging and plastic molding. |
This table highlights the key differences between elasticity and plasticity, which are important concepts in physics, especially when studying the mechanical properties of materials.
Also Read: Equilibrium Of A Rigid Body
Application of Elastic Behaviour of Solids
When we talk about the elastic behavior of solids, we’re looking at how materials can stretch, compress, or bend and then return to their original shape. This isn’t just a cool party trick; it’s a property that we rely on for tons of everyday applications. Let’s check out some of them:
Bridges and Buildings: Ever wonder why bridges don’t just snap when heavy trucks drive over them? That’s thanks to the elasticity of the materials they’re made from. They can flex a bit under the weight and then go right back to normal.
Vehicles: The shocks in your car are like big springs. They absorb the bumps on the road by compressing and then expand back, giving you a smooth ride.
Sports: The strings in a tennis racket, the pole in pole vaulting, and even the mat in gymnastics—all of these use the elastic behavior of materials to help athletes perform their best.
Medical Devices: Elastic materials are super important in medicine too. Think about the tiny springs in braces that move teeth into place, or the stents that keep blood vessels open.
Electronics: Your phone screen can bend a tiny bit if you press on it. That’s because it’s made from slightly elastic materials, which helps prevent it from breaking.
Clothing: Elastic bands in clothes make them stretchy and comfortable. They fit better because the material can expand and contract as you move.
Everyday Items: Rubber bands, bouncy balls, and even the mattress you sleep on—all of these rely on elastic materials to function the way they do.
Solved Examples
Example 1: A steel wire of length 1 meter and diameter 2 mm is stretched by a force of 100 N. If Young’s modulus of steel is (2 ×s 1011) N/m², calculate the extension produced in the wire.
Solution: Given;
- Length of the wire, (L = 1) m
- Diameter of the wire, (d = 2) mm = (2 × 10-3) m
- Force applied, (F = 100) N
- Young’s modulus of steel, (Y = 2 × 1011) N/m²
First, we need to find the cross-sectional area of the wire:
\(\displaystyle A = \frac{\pi d^2}{4} \)
\(\displaystyle A = \frac{\pi \times (2 \times 10^{-3})^2}{4} \)
\(\displaystyle A = \frac{\pi \times 4 \times 10^{-6}}{4} \)
\(\displaystyle A = \pi \times 10^{-6} \, m^2 \)
Now, we can use Hooke’s law to find the extension:
\(\displaystyle F = \frac{Y \cdot \Delta L}{L} \)
\(\displaystyle \Delta L = \frac{F \cdot L}{Y} \)
\(\displaystyle \Delta L = \frac{100 \times 1}{2 \times 10^{11}} \)
\(\displaystyle \Delta L = \frac{100}{2 \times 10^{11}} \)
\(\displaystyle \Delta L = 5 \times 10^{-10} \, m \)
So, the extension produced in the wire is (5 × 10-10) meters.
Example 2: A spring of spring constant (500 N/m) is stretched by (0.1 m) from its equilibrium position. Find the force required to stretch the spring by an additional (0.05 m).
Solution: Given;
- Spring constant, (k = 500 N/m)
- Initial extension, (∆x1 = 0.1 m)
- Additional extension, (∆x2 = 0.05 m)
The force required to stretch a spring is given by Hooke’s law:
\(\displaystyle F = k \cdot \Delta x \)
For the initial extension:
\(\displaystyle F_1 = k \cdot \Delta x_1 \)
\(\displaystyle F_1 = 500 \cdot 0.1 \)
\(\displaystyle F_1 = 50 \, N \)
Now, for the additional extension:
\(\displaystyle F_2 = k \cdot \Delta x_2 \)
\(\displaystyle F_2 = 500 \cdot 0.05 \)
\(\displaystyle F_2 = 25 \, N \)
So, the force required to stretch the spring by an additional (0.05 m) is (25 N).
Example 3: A rubber band has a length of (20 cm) and a cross-sectional area of (1 cm2). If a force of (5 N) is applied to the rubber band, calculate the strain produced in the rubber band. Given that the Young’s modulus of rubber is (5 × 106 N/m2).
Solution: Given;
- Length of the rubber band, (L = 20 cm = 0.2 m)
- The cross-sectional area of the rubber band, (A = 1 cm2 = 1× 10-4m2)
- Force applied, (F = 5 N)
- Young’s modulus of rubber, (Y = 5 ×106 N/m2)
The strain (\(\displaystyle\epsilon)\) produced in the rubber band is given by:
\(\displaystyle \epsilon = \frac{\Delta L}{L} \)
From Hooke’s Law, we know:
\(\displaystyle F = \frac{Y \cdot \Delta L}{L} \)
\(\displaystyle \Delta L = \frac{F \cdot L}{Y} \)
Substitute the values:
\(\displaystyle \Delta L = \frac{5 \times 0.2}{5 \times 10^6} \)
\(\displaystyle \Delta L = 2 \times 10^{-7}\, m \)
Now, calculate the strain:
\(\displaystyle \epsilon = \frac{2 \times 10^{-7}}{0.2} \)
\(\displaystyle \epsilon = 1 \times 10^{-6} \)
So, the strain produced in the rubber band is (1 × 10-7).
FAQs
Can you explain the difference between elastic and plastic deformation in solids?
Elastic deformation is reversible and temporary, where the material returns to its original shape after the stress is removed. On the other hand, plastic deformation is irreversible, causing a permanent change in shape. Elastic deformation occurs when the applied stress is below the material’s yield point, while plastic deformation occurs beyond this point.
How does Hooke’s Law relate to the elastic behavior of solids?
Hooke’s Law states that the strain in a material is directly proportional to the stress applied to it, as long as the material remains within its elastic limit. This law forms the basis of understanding elastic behavior, providing a linear relationship between stress and strain for elastic materials.
What factors influence the elastic behavior of solids?
Several factors influence elastic behavior, including the material’s composition, crystalline structure, temperature, and the presence of defects such as dislocations or vacancies. Additionally, the loading conditions, such as the rate of applying stress and the duration of loading, can also affect how a material responds elastically.
How does Poisson’s ratio contribute to understanding the elastic behavior of solids?
Poisson’s ratio (ν) describes the lateral contraction of a material when subjected to tensile or compressive stress. It quantifies the ratio of transverse strain to longitudinal strain. Understanding Poisson’s ratio helps predict how a material will deform in response to applied stress, providing insights into its elastic properties.ν
How does temperature affect the elastic behavior of solids?
Temperature influences the elastic behavior of solids by altering the vibrational motion of atoms or molecules within the material. At higher temperatures, increased thermal energy can disrupt bonds and lattice structures, leading to changes in the material’s stiffness and elastic properties. Additionally, temperature variation can affect the material’s coefficient of thermal expansion, influencing its response to mechanical stress.