The concept of elasticity dates back to the early scientific explorations of materials. Robert Hooke, an English scientist, first expressed the idea in 1676 with Hooke’s Law, stating that the extension of a spring is in direct proportion to the load applied to it.
Imagine living in a world where we didn’t understand why bridges don’t collapse under their own weight or how springs in a mattress can support us. This was the reality before the concept of elasticity was understood.
The journey began with Leonhard Euler, a Swiss scientist who, in 1727, laid down the principle of the modulus of elasticity. But it was an Italian scientist, Giordano Riccati, who in 1782, through his experiments, led to the calculations related to the modulus.
Fast forward to the 19th century, and we meet Thomas Young, a British scientist. Although he wasn’t the first to study the concept, he published detailed accounts in 1807, and hence the term Young’s Modulus became widely recognized.
Over time, scientists realized that materials could be stretched, compressed, and twisted in various ways, leading to the identification of different types of Elastic Moduli, like Young’s Modulus, Bulk Modulus, and Shear Modulus.
What is the Elastic Modulus
Elastic Modulus, also known as modulus of elasticity, is a measure of a material’s ability to resist deformation under load. It’s a way to quantify how much a material will stretch or compress when a force is applied.
Imagine you have a spring. You pull on it, and it stretches. You let it go, and it bounces back to its original shape. That ability of the spring to return to its original shape after being stretched or squished is all thanks to its elasticity.
Now, the Elastic Modulus is like a score that tells us how good a material is at being elastic. It’s a number that we calculate by looking at how much force it takes to stretch or squish something and how much it stretches or squishes.
\(\displaystyle\begin{equation}\label{eqn:1}\boxed{\boldsymbol{Elastic\ Modulus (E) = \frac{Stress (\sigma)}{Strain (\epsilon)} }} \end{equation}\)
- Stress is the force you apply to an object divided by the area over which you apply that force.
- Strain is how much the object stretches or squishes compared to its original length.
So, if you have two materials and you apply the same force to both, the one that stretches less has a higher Elastic Modulus. It’s stiffer and doesn’t like to change shape as much.
In other words, the Elastic Modulus tells us about the stiffness of a material. A high Elastic Modulus means the material is very stiff (like steel), and a low Elastic Modulus means the material is very flexible (like rubber).
Unit of Modulus of Elasticity
When we talk about the Elastic Modulus, we’re talking about how much force can a material handle before it starts to change shape. Now, to measure this, we need a unit, just like we use meters for distance and seconds for time.
The unit for the Elastic Modulus is the Pascal (Pa). It’s named after Blaise Pascal, a famous mathematician and physicist. One Pascal is pretty small, so we often use megapascals (MPa) or gigapascals (GPa) for bigger numbers.
So, when you see a material with a high number of Pascals for its Elastic Modulus, think of it as a really strong material that doesn’t squish or stretch easily. It’s like comparing a hard diamond to a squishy marshmallow.
Types of Elastic Modulus
When we talk about Elastic Modulus, we’re looking at how materials behave when forces are applied to them. Three main types tell us about different kinds of behavior:
Young’s Modulus (E)
This one is all about stretching or compressing. Imagine pulling on both ends of a rubber band; how much it stretches is what Young’s Modulus measures. It’s like the material’s willingness to be stretched or squished along its length.
Imagine you have a rubber band in your hand. If you pull on it, it stretches, right? Now, if you had a steel wire of the same thickness and pulled it with the same force, it wouldn’t stretch as much as the rubber band. This difference in stretchiness is what Young’s Modulus helps us measure.
Young’s Modulus (often represented as E) is a way to measure how stiff a material is. It’s a number that tells us how much a material will stretch (or compress) when we apply a force to it.
\(\displaystyle E = \frac{\text{Stress}}{\text{Strain}} \)
Because it tells us super important stuff! Like, if you’re building a bridge, you want to use materials that won’t stretch or bend too much under the weight of cars, right? Young’s Modulus helps engineers figure out which materials are best for the job.
Materials with a high Young’s Modulus are stiff, like diamond or steel. They don’t like to stretch or squish. Materials with a low Young’s Modulus, like rubber or sponge, are much more flexible.
Determination of Young’s Modulus of the Material of a Wire:
Imagine you’re in a lab with a metal wire hanging from a fixed support. You’re about to find out how stiff this wire is, and that’s where Young’s Modulus comes in.
You have A wire of known length and diameter., Weights to apply force to the wire. A micrometer to measure tiny changes in the wire’s length.
- Hang the Wire: Secure the wire at one end to a rigid support.
- Measure Original Length: Note down the wire’s original length (let’s call it (L0).
- Add Weights: Hang a weight at the other end of the wire and let gravity do its thing. The weight pulls the wire, stretching it slightly.
- Measure Extended Length: After the wire stretches, measure the new length (let’s call it (L).
- Calculate Change in Length: Find the difference between the original and extended lengths (Δ L = L – L0).
Now, you use the formula for Young’s Modulus (Y):
\(\displaystyle Y = \frac{\text{Stress}}{\text{Strain}} \)
So, you plug in the numbers, and voilà, you’ve determined the Young’s Modulus for the wire! This experiment helps us understand how different materials respond to stress. It’s like a personality test for materials, telling us who’s the stiff one and who’s more laid-back under pressure.
Derivation:
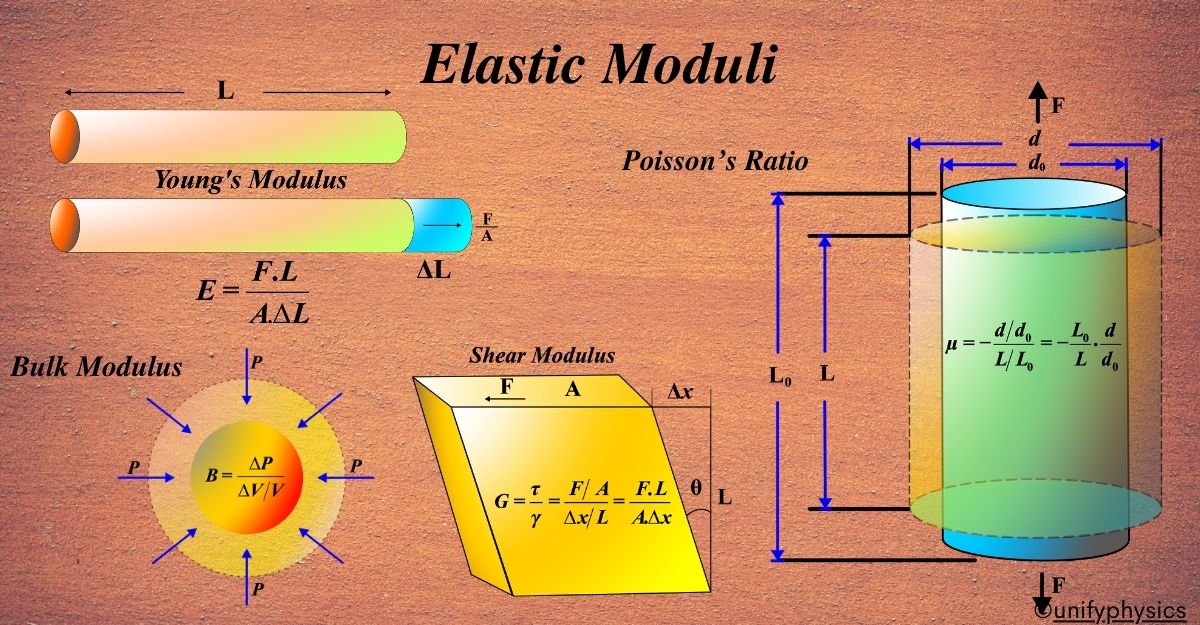
Young’s Modulus is a measure of the stiffness of a material. It tells us how much a material will stretch (or compress) when a force is applied to it. The formula for Young’s Modulus is:
\(\displaystyle E = \frac{\text{Stress}}{\text{Strain}} \)
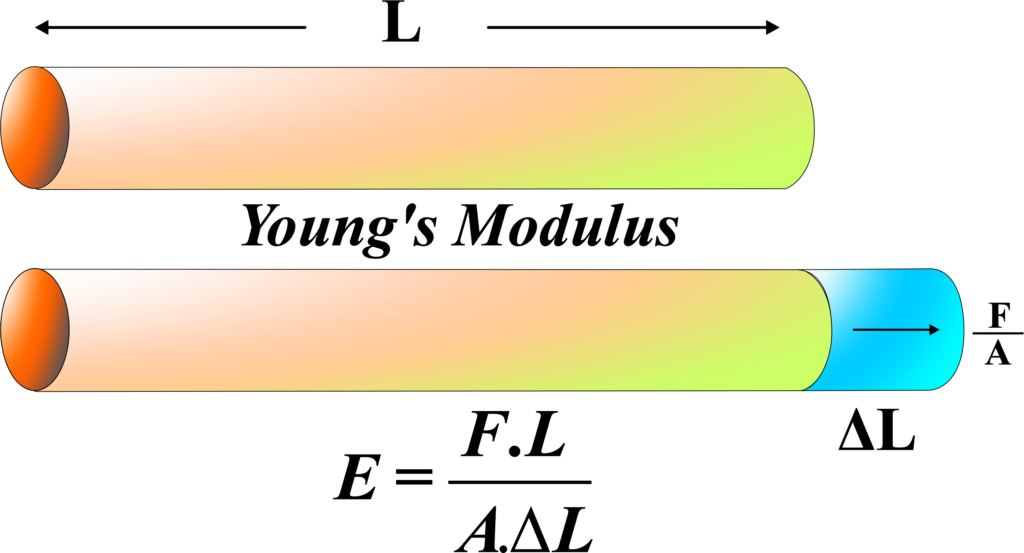
Stress is the force applied to an object divided by the area over which the force is applied. It’s like how hard you’re pushing or pulling on something. In a formula, it looks like this:
\(\displaystyle\text{Stress} (\sigma) = \frac{\text{Force (F)}}{\text{Area (A)}}\)
Strain is how much the object stretches or compresses compared to its original length. It’s a ratio, so there are no units for strain. Here’s the formula:
\(\displaystyle\text{Strain} (\epsilon) = \frac{\text{Change in Length} (\Delta L)}{\text{Original Length} (L_0)}\)
Now, if we take the formula for stress and the formula for strain and put them into the Young’s Modulus equation, we get:
\(\displaystyle E = \frac{\frac{F}{A}}{\frac{\Delta L}{L_0}}\)
Simplifying this, we multiply both the numerator and the denominator by (L_0) and divide both by (∆ L), which gives us:
\(\displaystyle\begin{equation}\label{eqn:2}\boxed{\boldsymbol{ E = \frac{F \cdot L_0}{A \cdot \Delta L}}} \end{equation}\)
And there you have it! This is the expression for Young’s Modulus. It tells us how stiff a material is by relating the force applied to how much it stretches. A high value of (E) means the material is very stiff and doesn’t stretch much. A low value means the material is more flexible.
Young’s moduli and yield strengths of some materials are,
| Materials | Young’s Modulus (GPa) | Elastic Limit (MPa) | Tensile Strength (MPa) |
|---|---|---|---|
| ABS plastics | 1.4 – 3.1 | – | 40 |
| Aluminum | 69 | 95 | 110 |
| Brass | 102 – 125 | – | 250 |
| Concrete | 17 | 40 (compression) | – |
| Copper | 117 | 70 | 220 |
| Glass | 50 – 90 | 50 (compression) | – |
| Steel | 210 | – | – |
| Wood (Douglas fir) | 13 | 50 (compression) | – |
- Young’s Modulus (E): This tells us how stiff the material is. Higher numbers mean the material is stiffer and doesn’t stretch or compress easily.
- Elastic Limit: This is the maximum stress that a material can withstand without permanently deforming. When we talk about compression, it’s the same idea but with squishing instead of stretching.
- Tensile Strength: This is the maximum stress a material can handle before it breaks when being pulled apart.
Determination of Young’s Modulus of the Material of a Wire
This is typically done using a tensile test where a sample wire is stretched, and the amount of stretching (strain) is measured against the force applied (stress).
The Modulus of Elasticity (or Young’s Modulus) is like a material’s “stretchiness score.” It tells us how much a material will stretch or compress when we apply a force to it. Named after Thomas Young, who introduced it in 1807, this property helps us understand how materials behave under stress.
Robert Hooke, an early scientist, discovered that within the elastic range of a material, strain (deformation) is directly proportional to stress (applied force). This relationship is known as Hooke’s Law, and the Modulus of Elasticity plays a starring role in it.
The Modulus of Elasticity quantifies a material’s stiffness or rigidity. High values mean the material is super stiff (like steel), while low values mean it’s more flexible (like rubber).
When we plot stress against strain for most materials, we get a linear relationship within the elastic region. The slope of this line (up to the proportional limit) gives us the Modulus of Elasticity.
Elastic materials return to their original shape after deformation. The Modulus of Elasticity helps predict how much a material will deform under stress—essential for designing structures and components.
Bulk Modulus (K)
Now, think about squeezing a sponge all around evenly. The Bulk Modulus is about how willing the material is to be squished in all directions without changing its volume too much. It’s like how resistant it is to being pushed in from all sides.
Imagine you have a squishy stress ball. When you squeeze it, it gets smaller. But what if you had a super-hard rock? If you tried to compress it, it wouldn’t budge much. That’s where the Bulk Modulus comes into play.
The Bulk Modulus is like a superhero power possessed by materials. It measures how much a solid or fluid resists changes in volume when pressure is applied from all sides. Think of it as the material’s ability to stay put when you squish it or press on it equally from all directions.
Elasticity vs. Plasticity:
- Elasticity: Imagine a rubber band. When you stretch it, it bounces back. That’s elasticity. Materials that regain their original shape after being squished or stretched are elastic.
- Plasticity: Now, mud or putty doesn’t bounce back. It stays deformed. These materials are plastic—they don’t care about returning to their original shape.
When you apply pressure to a material (like squeezing a sponge), it might compress or expand a little. The Bulk Modulus tells us how much it resists this volume change. High Bulk Modulus means it’s super resistant (like a rock), while low Bulk Modulus means it’s more squishy (like a stress ball).
Mathematically, the Bulk Modulus (B) is the ratio of the change in pressure to the fractional volume compression:
\(\displaystyle\begin{equation}\label{eqn:3}\boxed{\boldsymbol{ B = \frac{\Delta P}{\frac{\Delta V}{V}}}} \end{equation}\)
Example: Let’s say a material experiences a pressure change of \(\displaystyle 5 \times 10^4 \, \text{N/m}^2\), and its volume goes from \(\displaystyle 4 \, \text{cm}^3) to (3.9 \, \text{cm}^3\).
We calculate the Bulk Modulus:
\(\displaystyle B = \frac{\Delta P}{\frac{\Delta V}{V}} = \frac{5 \times 10^4 \, \text{N/m}^2}{\frac{(4 \, \text{cm}^3 – 3.9 \, \text{cm}^3)}{4 \, \text{cm}^3}} = 0.125 \times 10^4 \, \text{N/m}^2 \)
\(\displaystyle B = 1.25 \times 10^4 \, \text{N/m}^2 \)
Bulk Modulus helps us understand how much a solid or fluid can withstand pressure without squishing or expanding.
For example, steel has a high Bulk Modulus \(\displaystyle 1.6 × 10^11 N/m^2\), making it tough to compress. Glass, with a lower Bulk Modulus \(\displaystyle 4 × 10^10 N/m^2 \), is more squishy.
Compressibility:
Imagine you have a sponge and a steel block. If you try to squeeze both, the sponge compresses easily, but the steel block? Not so much. This difference in “squishiness” is what we call Compressibility.
Compressibility is a measure of how much a material can be squished. It’s like a squishiness score for materials. It’s represented by the symbol (k) and tells us how a material will change in volume under pressure.
The Bulk Modulus is the opposite of compressibility. It measures how resistant a material is to being compressed. It’s like a toughness score for materials against being squished. When we say Compressibility is the reciprocal of the Bulk Modulus, we mean:
\(\displaystyle\begin{equation}\label{eqn:4}\boxed{\boldsymbol{k = \frac{1}{B} }} \end{equation}\)
This means if you have a high Bulk Modulus (like steel), the Compressibility will be low because it’s tough to squish. Conversely, if you have a low Bulk Modulus (like a sponge), the Compressibility will be high because it’s easy to squish.
The bulk moduli of a few common materials are given in the table below.
| Materials | Bulk Modulus (B) |
|---|---|
| Aluminum | 70 GPa |
| Brass | 108 – 116 GPa |
| Copper | 123 GPa |
| Iron | 58 – 107 GPa |
| Lead | 46 GPa |
| Steel | 160 GPa |
Note:
- Bulk Modulus (B): This value tells us how much a material resists being squished. It’s like measuring how tough it is to squeeze a sponge versus a rock. Higher numbers mean the material is more resistant to being compressed.
Shear Modulus (G)
Have you ever tried to cut through a piece of cheese? The Shear Modulus is about how a material behaves when you apply a force that tries to slide one part of it over another part. It’s like measuring how easy it is to cut or slide through the material.
Imagine you’re holding a thick rubber band. Now, instead of stretching it lengthwise, twist it around its axis. Notice how it resists twisting? That’s where the Shear Modulus comes into play.
The Shear Modulus, also known as the Modulus of Rigidity, measures a material’s resistance to lateral deformation when a shearing force is applied. Think of it as the material’s ability to stay firm when you twist or slide its layers past each other.
Elasticity vs. Plasticity:
- Elasticity: Remember the rubber band? It bounces back after stretching. Elastic materials regain their original shape.
- Plasticity: Now, imagine soft clay. When you twist it, it stays twisted. These materials are plastic—they don’t spring back.
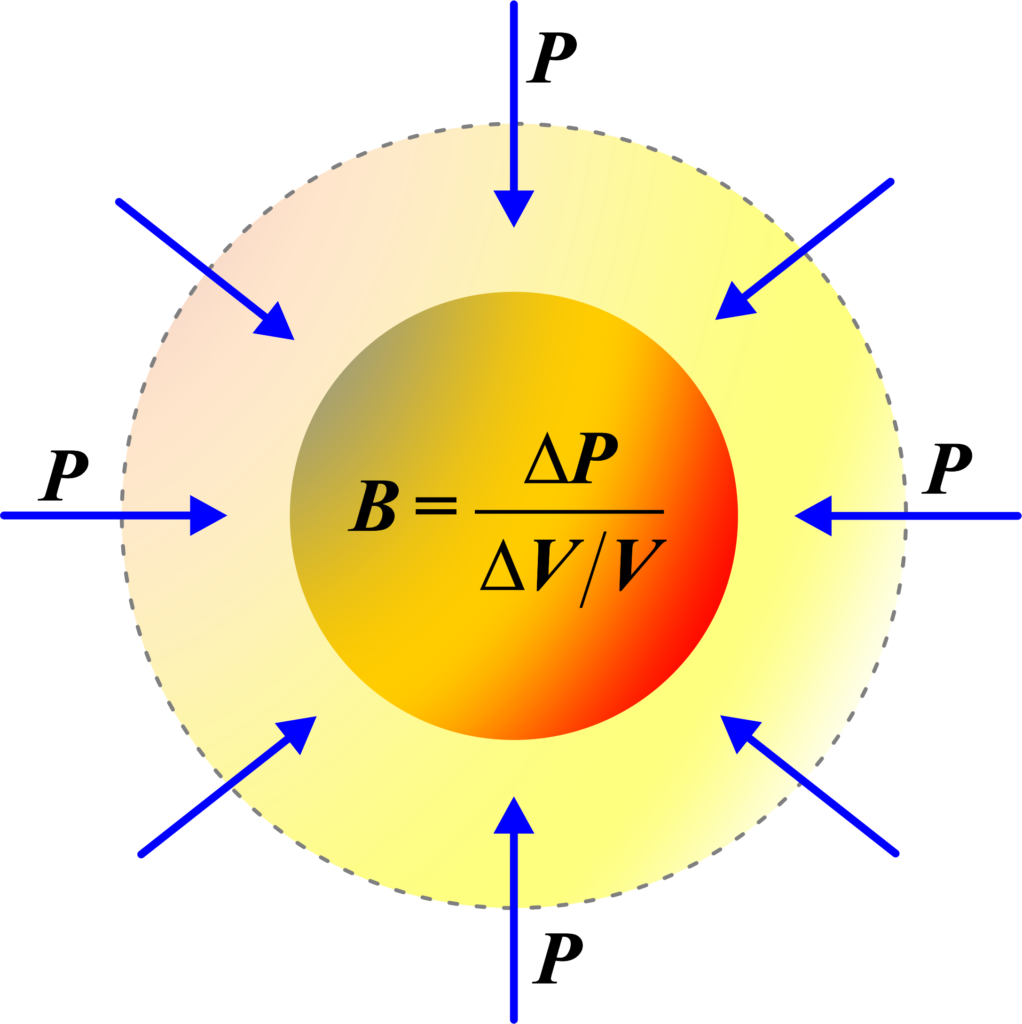
Apply a shearing force (like twisting) to a material. The Shear Modulus tells us how much it resists this twisting. High Shear Modulus means it’s super rigid (like steel), while low Shear Modulus means it’s more twistable (like rubber). Mathematically, the Shear Modulus (G) is the ratio of shear stress to shear strain:
\(\displaystyle\begin{equation}\label{eqn:10}\boxed{\boldsymbol{ G = \frac{\tau}{\gamma} = \frac{F/A}{\Delta x/L} = \frac{F \cdot L}{A \cdot \Delta x} }} \end{equation}\)
- (G) is the Shear Modulus,
- (τ) is the shear stress,
- (γ) is the shear strain,
- (F ) is the force applied parallel to the surface,
- (A) is the area over which the force is applied,
- (∆x) is the transverse displacement,
- (L) is the initial length of the material.
When considering the angle of deformation, (θ), which is the angle by which the material deforms due to the applied force, the shear strain can be expressed as the tangent of this angle for small deformations. Here’s the formula incorporating the angle (θ):
\(\displaystyle\begin{equation}\label{eqn:11}\boxed{\boldsymbol{G = \frac{\tau}{\gamma} = \frac{F/A}{\tan(\theta)} }} \end{equation}\)
- (θ) is the angle of deformation.
For small angles of deformation, where (θ) is small enough that \(\displaystyle \tan(\theta) \approx \theta \) (in radians), the formula can be simplified to:
\(\displaystyle G = \frac{F/A}{\theta} \)
This relationship allows us to calculate the Shear Modulus if we know the applied force, the area over which it’s applied, and the angle of deformation due to the force.
Example:
- Wood has a Shear Modulus of about \(\displaystyle 6.2 \times 10^8 \, \text{Pa}\).
- Steel, on the other hand, boasts a whopping \(\displaystyle 7.2 \times 10^{10} \, \text{Pa}\) Shear Modulus.
- Translation: Steel is around 127 times more rigid than wood!
Real-World Applications:
- Structural Stability: Engineers use Shear Modulus to design sturdy bridges, buildings, and even airplane wings.
- Material Selection: It helps choose materials for gears, springs, and anything that experiences twisting forces.
The shear moduli of a few common materials are given in the table below.
| Materials | Shear Modulus (G) |
|---|---|
| Aluminum | 25 GPa |
| Brass | 35 GPa |
| Copper | 44 GPa |
| Iron | 77 GPa |
| Lead | 6 GPa |
| Silicone Rubber | 0.002 GPa |
| Steel | 75 GPa |
Note:
- Shear Modulus (G): This value tells us how much a material resists being deformed when a force is applied parallel to one of its surfaces. It’s like measuring how tough it is for you to slide two stacked books over each other. Higher numbers mean the material is more resistant to shearing.
Also Read: Elastic Behavior Of Solids
Poisson’s Ratio (μ)
Poisson’s ratio is “the ratio of transverse contraction strain to longitudinal extension strain in the direction of the stretching force.”
Poisson’s Ratio is a way to measure how much a material’s width (or thickness) changes when you stretch or compress it lengthwise. It’s named after the French mathematician Siméon Poisson.
Imagine you have a rubber band. When you pull it to stretch, not only does it get longer, but it also gets thinner in the middle. Poisson’s Ratio is all about this width change when you stretch something.
\(\displaystyle \mu = -\frac{\text{Transverse Strain}}{\text{Longitudinal Strain}} \)
- Transverse Strain is the change in width divided by the original width.
- Longitudinal Strain is the change in length divided by the original length.
The negative sign is there because when something stretches and gets longer (positive longitudinal strain), it usually gets thinner (negative transverse strain).
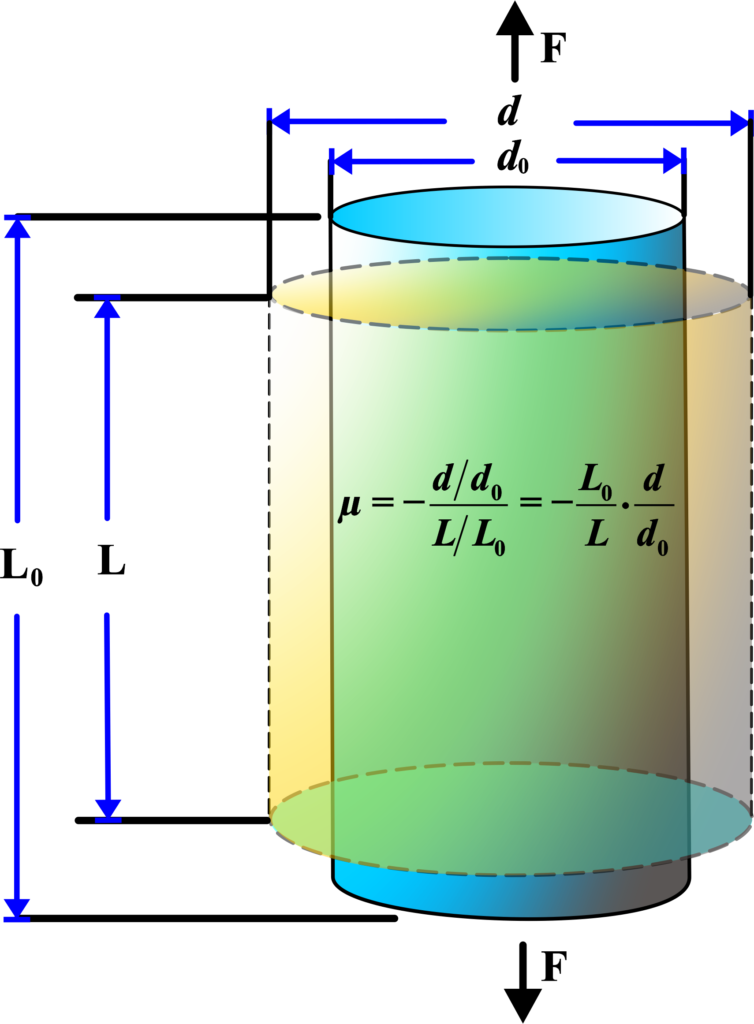
The minus sign makes sure that for most materials, which get thinner when stretched, the value of Poisson’s Ratio is positive.
Poisson’s Ratio (μ) is the ratio of lateral or transverse strain to longitudinal or axial strain. It describes how a material changes in width (lateral direction) when stretched or compressed (longitudinal direction).
The formula for Poisson’s Ratio is:
\(\displaystyle\begin{equation}\label{eqn:14}\boxed{\boldsymbol{\mu = -\frac{{\frac{{d}}{{d_0}}}}{{\frac{{L}}{{L_0}}}} = -\frac{{L_0}}{{L}} \cdot \frac{{d}}{{d_0}} }} \end{equation}\)
- (µ) represents Poisson’s Ratio.
- (d) is the change in width (transverse displacement).
- (d0 ) is the original width.
- (L) is the change in length (longitudinal displacement).
- (L0) is the original length.
For most materials, Poisson’s Ratio is between 0 and 0.5. A value of 0 means the material doesn’t change in width at all when stretched. A value of 0.5 means the volume stays the same during deformation, so if it gets longer, it must get thinner to keep the volume constant.
Examples
- When you blow up a balloon, it stretches in all directions. The rubber gets thinner as it expands—that’s Poisson’s Ratio in action!
- When you step on a sponge, it flattens, but it also expands outward. That’s because the sponge’s Poisson’s Ratio tells it to get wider when compressed.
So, Poisson’s Ratio helps us understand how materials will behave when they’re stretched or squished. It’s super important for engineers when they’re designing things like car tires, building materials, and even sports equipment.
Resilient Modulus
This measures the elastic response of materials under repeated loads, often used in the context of roadbed materials.
Imagine you’re playing with a super bouncy ball. You drop it, and it hits the ground and bounces back up almost to the height from which you dropped it. This ball is showing resilience—it’s not getting squished or deformed; it’s bouncing back!
The Resilient Modulus is a measure of how well a material can recover its shape after a quick squeeze or stretch. It’s like the Modulus of Elasticity, but for rapid, repeated loads, like what pavement experiences when cars and trucks zoom over it.
Elasticity vs. Resilience:
- Elasticity: This is about slowly applying a load and seeing how the material stretches or compresses.
- Resilience: This is about quickly applying a load and seeing if the material can bounce back without any permanent change.
We use a test called the triaxial test. It’s like giving the material a quick squeeze and then letting go to see how well it returns to its original shape. The test applies a repeated load, kind of like bouncing a ball, and measures how the material responds.
It’s super important for things like roads and runways. We want them to be able to handle the traffic without getting permanent dents or bumps. It helps engineers design materials that can take a lot of hits and still keep their cool.
Think about a road. It has to be resilient enough to bounce back after every car or truck passes over it. If it wasn’t, we’d have a very bumpy ride. So, the Resilient Modulus is like a score for how well materials can handle the stress of everyday life—like a bouncy ball for the real world.
Elastic Constants
These are values that relate to stress and strain and determine the material’s deformation response. Think of a building. It has to stand tall and strong, right? Now, what if we could measure exactly how strong each brick in that building is? That’s what Elastic Constants do for materials.
Elastic Constants are like the secret codes that tell us how a material will behave when we push, pull, or twist it. They are the superhero team of the material world, each with a special power to resist different kinds of forces.
- Young’s Modulus (E): This is the leader of the team. It tells us how much a material will stretch or compress under a pulling or pushing force.
- Bulk Modulus (K): This is the tough one. It measures how hard it is to squish a material from all sides.
- Shear Modulus (G): The ninja of the group. It tells us how a material will hold up when you try to slide its layers past each other.
- Poisson’s Ratio (μ): The shapeshifter. It describes how a material will expand or contract sideways when it’s stretched or compressed.
These constants are all related. Knowing two of them can help you figure out the others. They work together to give us a full picture of a material’s strength and flexibility.
Mathematical Relationship Between Elastic Constants:
Think of Elastic Constants as a team of superheroes, each with a special power. They work together to keep materials strong and resilient. Here’s how they are related mathematically:
Between E and G: \(\displaystyle\begin{equation}\label{eqn:6}\boxed{\boldsymbol{E = 2G(1 + \mu) }} \end{equation}\)
This equation connects Young’s Modulus (E) with Shear Modulus (G) and Poisson’s Ratio (μ). It tells us how the stiffness of a material relates to its ability to resist shearing and its sideways expansion or contraction.
Between E and K: \(\displaystyle\begin{equation}\label{eqn:7}\boxed{\boldsymbol{ E = 3K(1 – 2\mu)}} \end{equation}\)
Here, we see how Young’s Modulus (E) is related to Bulk Modulus (K) and Poisson’s Ratio (μ). It’s about how the stiffness of a material is influenced by its resistance to volume change and its sideways behavior.
Between E, G, and K: \(\displaystyle\begin{equation}\label{eqn:8}\boxed{\boldsymbol{ E = \frac{9KG}{3K + G}}} \end{equation}\)
This one’s a bit like a team strategy. It shows how Young’s Modulus (E) can be determined if we know both the Shear Modulus (G) and the Bulk Modulus (K). It’s a combo move that gives us a complete picture of the material’s strength.
Poisson’s Ratio (μ) in terms of K and G: \(\displaystyle\begin{equation}\label{eqn:9}\boxed{\boldsymbol{\mu = \frac{3K – 2G}{6K + 2G} }} \end{equation}\)
This formula is like a secret code that lets us find out Poisson’s Ratio (μ) if we know the Bulk Modulus (K) and the Shear Modulus (G). It’s about understanding how a material will behave sideways when we pull or push it.
Examples of the Elastic Modulus
Think of Elastic Modulus as a way to rate different materials on how much they can stretch or squish when you apply force to them. Here are some examples with their Elastic Modulus values:
- Steel: The superhero of construction materials! It has an Elastic Modulus of about 210 GPa (gigapascals). That’s why it’s used in skyscrapers and bridges—it doesn’t bend or stretch easily under heavy loads.
- Concrete: The backbone of modern cities, concrete has an Elastic Modulus ranging from 30 to 50 GPa. It’s strong but not as stiff as steel, which is why it’s often reinforced with steel rods.
- Aluminum: Light and strong, aluminum has an Elastic Modulus of around 70 GPa. It’s used in airplanes and soda cans because it’s pretty stiff but also lightweight.
- Wood: Nature’s building material, wood has an Elastic Modulus that can vary from 5.5 GPa to 17 GPa depending on the type. It’s used in furniture and houses because it’s strong but also has a bit of give.
- Plastic (Polystyrene): Commonly used in packaging, polystyrene has an Elastic Modulus of about 3 GPa. It’s flexible and can absorb some impact, which is why it’s great for protecting items during shipping.
These values give us an idea of how different materials will behave when forces are applied to them. A higher Elastic Modulus means the material is stiffer and less likely to deform.
Applications of Elastic Moduli?
Understanding the elastic properties of materials is crucial in fields like civil engineering, materials science, and mechanical engineering. It helps in designing structures, machinery, and even everyday objects to ensure they can withstand the forces they’ll encounter.
- Building Skyscrapers: Just like a spine keeps us upright, steel beams with high Young’s Modulus keep skyscrapers from bending over in the wind. They’re the reason buildings can reach the sky without swaying too much.
- Designing Bridges: When engineers design bridges, they use materials with the right Elastic Moduli to make sure the bridge can support the weight of cars and trucks without sagging or bouncing too much.
- Creating Sports Equipment: Ever wonder why tennis rackets and golf clubs feel so good when you hit the ball? It’s because they’re made with materials that have the perfect balance of stiffness and flexibility, thanks to their Elastic Moduli.
- Making Medical Devices: The Elastic Modulus is crucial in designing medical implants like hip replacements. They need to be strong enough to support the body but also flexible enough to move with it.
- Aerospace Engineering: Airplanes and rockets need materials that can handle the stress of takeoff and the pressure changes in the atmosphere. The Elastic Moduli of materials help ensure they don’t crack under pressure.
- Automobile Manufacturing: Cars are designed with materials that have specific Elastic Moduli to absorb the shock of bumps and protect passengers during a crash.
- Everyday Objects: Even the phone in your pocket or the chair you’re sitting on has been designed considering the Elastic Moduli of materials. It’s all about finding the right balance to make them durable and comfortable.
- Civil Engineering: In the construction of structures like dams, tunnels, and towers, the Elastic Moduli helps predict how these massive structures will behave under various loads and stresses.
- Material Science: Understanding the Elastic Moduli is key in developing new materials that can lead to the next generation of technology, from flexible electronics to more efficient solar panels.
Solved Examples
Example 1: A steel wire of length 2 meters and diameter 2 mm is stretched by a force of 500 N. If Young’s modulus of steel is \(\displaystyle 2 \times 10^{11} \, \text{N/m}^2\), calculate the longitudinal strain produced in the wire.
Solution: Given;
- Length of the wire, (L = 2 m)
- Diameter of the wire, (d = 2 mm = 0.002 m)
- Applied force, (F = 500 N)
- Young’s modulus of steel, \(\displaystyle Y = 2 \times 10^{11} \, \text{N/m}^2\)
First, we find the cross-sectional area of the wire:
\(\displaystyle A = \frac{\pi d^2}{4} = \frac{\pi \times (0.002)^2}{4} = \frac{\pi \times 0.000004}{4} = \frac{\pi}{10000} \, \text{m}^2 \)
Now, we use Hooke’s law to find the longitudinal strain (\(\displaystyle\epsilon\)):
\(\displaystyle \epsilon = \frac{F}{Y \times A} = \frac{500}{2 \times 10^{11} \times \frac{\pi}{10000}} \)
\(\displaystyle \epsilon = \frac{500 \times 10000}{2 \times 10^{11} \times \pi} \)
\(\displaystyle \epsilon \approx 7.96 \times 10^{-4} \)
So, the longitudinal strain produced in the wire is approximately \(\displaystyle7.96 \times 10^{-4}\).
Example 2: A rubber block with a volume of \(\displaystyle 500 \, \text{cm}^3\) is subjected to a compressive force of (200 N). If the bulk modulus of rubber is \(\displaystyle 10^6 \, \text{N/m}^2\), calculate the decrease in volume of the block.
Solution: Given:
- Initial volume of the rubber block, \(\displaystyle V_0 = 500 \, \text{cm}^3 = 500 \times 10^{-6} \, \text{m}^3\)
- Applied force, \(\displaystyle F = 200 \, \text{N}\)
- Bulk modulus of rubber, \(\displaystyle B = 10^6 \, \text{N/m}^2\)
The decrease in volume (∆ V) can be calculated using the formula:
\(\displaystyle \Delta V = -\frac{V_0 \times F}{B} = -\frac{500 \times 10^{-6} \times 200}{10^6} \)
\(\displaystyle \Delta V = -0.1 \times 10^{-3} \, \text{m}^3 \)
So, the decrease in volume of the rubber block is \(\displaystyle 0.1 \times 10^{-3} \, \text{m}^3\).
Example 3: A copper wire of length (1 m) and diameter (1 mm) is stretched by a force of (100 N). If Young’s modulus of copper is \(\displaystyle 1.2 \times 10^{11} \, \text{N/m}^2\), calculate the tensile stress produced in the wire.
Solution: Given:
- Length of the wire, (L = 1 m)
- Diameter of the wire, (d = 1 mm = 0.001 m)
- Applied force, (F = 100 N)
- Young’s modulus of copper, \(\displaystyle Y = 1.2 \times 10^{11} \, \text{N/m}^2\)
First, we find the cross-sectional area of the wire:
\(\displaystyle A = \frac{\pi d^2}{4} = \frac{\pi \times (0.001)^2}{4} = \frac{\pi \times 0.000001}{4} = \frac{\pi}{4000000} \, \text{m}^2 \)
Now, we can calculate the tensile stress (σ):
\(\displaystyle \sigma = \frac{F}{A} = \frac{100}{\frac{\pi}{4000000}} = \frac{100 \times 4000000}{\pi} \, \text{N/m}^2 \approx 31831.97 \, \text{N/m}^2 \)
So, the tensile stress produced in the wire is approximately (31831.97 N/m2).
Example 4: A steel rod of length (2 m) and diameter (2 cm) is stretched by a force of (1000 N). If the Young’s modulus of steel is \(\displaystyle 2 \times 10^{11} \, \text{N/m}^2\), calculate the tensile strain produced in the rod.
Solution: Given;
- Length of the rod, (L = 2 m)
- Diameter of the rod, (d = 2 cm= 0.02 m)
- Applied force, (F = 1000 N)
- Young’s modulus of steel, \(\displaystyle Y = 2 \times 10^{11} \, \text{N/m}^2\)
First, we find the cross-sectional area of the rod:
\(\displaystyle A = \frac{\pi d^2}{4} = \frac{\pi \times (0.02)^2}{4} = \frac{\pi \times 0.0004}{4} = \frac{\pi}{10000} \, \text{m}^2 \)
Now, we can calculate the tensile strain \(\displaystyle\epsilon\):
\(\displaystyle \epsilon = \frac{F}{Y \times A} = \frac{1000}{2 \times 10^{11} \times \frac{\pi}{10000}} \)
\(\displaystyle \epsilon = \frac{1000 \times 10000}{2 \times 10^{11} \times \pi} \)
\(\displaystyle \epsilon \approx 7.96 \times 10^{-4} \)
So, the tensile strain produced in the rod is approximately \(\displaystyle 7.96 \times 10^{-4}\).
Example 5: A rubber block with a volume of \(\displaystyle 100 \, \text{cm}^3\) is subjected to a compressive force of (50 N). If the bulk modulus of rubber is \(\displaystyle 2 \times 10^6 \, \text{N/m}^2\), calculate the decrease in volume of the block.
Solution: Given;
- Initial volume of the rubber block, \(\displaystyle V_0 = 100 \, \text{cm}^3 = 100 \times 10^{-6} \, \text{m}^3\)
- Applied force, (F = 50 N)
- Bulk modulus of rubber, \(\displaystyle B = 2 \times 10^6 \, \text{N/m}^2\)
The decrease in volume ((\Delta V)) can be calculated using the formula:
\(\displaystyle \Delta V = -\frac{V_0 \times F}{B} = -\frac{100 \times 10^{-6} \times 50}{2 \times 10^6} \)
\(\displaystyle \Delta V = -0.0025 \times 10^{-3} \, \text{m}^3 \)
So, the decrease in volume of the rubber block is \(\displaystyle 0.0025 \times 10^{-3} \, \text{m}^3\).
Example 6: A copper wire of length (2m) and diameter (2 mm) is stretched by a force of (200 N). If Young’s modulus of copper is \(\displaystyle 1.2 \times 10^{11} \, \text{N/m}^2\), calculate the tensile stress produced in the wire.
Solution: Given;
- Length of the wire, (L = 2 m)
- Diameter of the wire, (d = 2 mm = 0.002 m)
- Applied force, (F = 200 N)
- Young’s modulus of copper, \(\displaystyle Y = 1.2 \times 10^{11} \, \text{N/m}^2\)
First, we find the cross-sectional area of the wire:
\(\displaystyle A = \frac{\pi d^2}{4} = \frac{\pi \times (0.002)^2}{4} = \frac{\pi \times 0.000004}{4} = \frac{\pi}{1000000} \, \text{m}^2 \)
Now, we can calculate the tensile stress (σ):
\(\displaystyle \sigma = \frac{F}{A} = \frac{200}{\frac{\pi}{1000000}} = \frac{200 \times 1000000}{\pi} \, \text{N/m}^2 \approx 63662.94 \, \text{N/m}^2 \)
So, the tensile stress produced in the wire is approximately \(\displaystyle 63662.94 \, \text{N/m}^2\).
FAQs
How do we determine which elastic modulus to use for different materials?
The choice of elastic modulus depends on the type of deformation a material undergoes. Young’s Modulus (Y) is used for describing the linear elastic behavior of a material under tensile or compressive stress. Shear Modulus (G) is employed for materials experiencing shear stress, such as in torsional or shear-loading situations. Bulk Modulus (K) is relevant for materials subjected to uniform pressure or volume changes, like fluids or gases.
What is the significance of Poisson’s Ratio in materials science?
Poisson’s Ratio (ν) quantifies the lateral contraction or expansion of a material when it is stretched or compressed along its length. It is essential in understanding how materials deform under various loading conditions and is particularly crucial in applications involving composite materials and structural engineering.
How does temperature affect the elastic moduli of materials?
Temperature influences the elastic moduli of materials by affecting their atomic or molecular structure and vibrational motion. Generally, an increase in temperature leads to a decrease in the elastic moduli of materials due to thermal expansion and the disruption of interatomic bonds. However, this effect varies depending on the material’s composition and crystal structure.
Can you explain why different materials exhibit different values of elastic moduli?
The elastic moduli of materials depend on factors such as the arrangement of atoms or molecules, interatomic or intermolecular forces, crystal structure, and chemical composition. For example, materials with strong atomic bonds tend to have higher elastic moduli, while those with weaker bonds exhibit lower moduli.
How do we experimentally determine the values of elastic moduli for a given material?
Experimental techniques such as tensile testing, compression testing, and shear testing are commonly used to determine the elastic moduli of materials. These tests involve applying controlled loads to a specimen and measuring its resulting deformation. The stress-strain data obtained from these tests can then be used to calculate the elastic moduli.
What are the practical applications of knowing the elastic moduli of materials?
Understanding the elastic moduli of materials is crucial in various engineering applications. For example, knowledge of Young’s Modulus helps in designing structures to withstand loads without undergoing excessive deformation. Shear Modulus is essential for designing components subjected to torsional or shear forces, while Bulk Modulus is relevant in applications involving fluid dynamics and hydraulic systems.
How does the elastic modulus change during the elastic deformation of a material?
During elastic deformation, the elastic modulus remains constant, as long as the material stays within its elastic limit. This means that the relationship between stress and strain, as described by Hooke’s Law, remains linear. Once the material exceeds its elastic limit and enters the plastic deformation region, the elastic modulus may change due to strain hardening or other factors.