Electric Field Due To A Point Charge

The idea of an electric field emerged in the mid-19th century, thanks to the pioneering work of Michael Faraday. Faraday introduced the concept to explain how a charged object, like a point charge, can influence the space around it without any physical contact.

A point charge is an idealized small object with a specific amount of charge. It’s called a ‘point’ charge because the size of the charge is so small that it can be considered to occupy a single point in space.

Faraday envisioned the electric field as a way to represent the force a charge exerts on other charges in its vicinity. This was a significant shift from the idea that charges had to touch each other to affect each other. Instead, Faraday’s field concept suggested that charges could exert forces over a distance, through the electric field.

The electric field due to a point charge is a perfect example of this concept. It’s described by Coulomb’s Law, which states that the electric field (E) created by a point charge (q) is directly proportional to the magnitude of the charge and inversely proportional to the square of the distance (r) from the charge.

This law is an inverse square law, meaning the strength of the field decreases with the square of the distance from the charge. The direction of the field is always away from a positive charge and towards a negative charge.

Faraday’s concept of the electric field due to a point charge has been fundamental in physics. It has paved the way for the development of various theories and technologies, including electric circuits and electrostatics. It’s a cornerstone in understanding how forces are transmitted over a distance and is a key concept in the study of electromagnetism.

Electric Field Due to a Point Charge

An electric field is created around any charged object. For a point charge, which is an idealized charge located at a single point in space, this field is a region where another charged object would experience a force. The strength and direction of the electric field depend on the amount of charge and the distance from the charge.

Imagine you have a single, isolated charge, let’s call it (Q). This charge can be either positive or negative. Now, this charge (Q) isn’t just sitting there; it’s doing something quite remarkable. It’s creating an invisible force field around itself, which we call the electric field.

This electric field is a vector field, which means it has both a magnitude (how strong it is) and a direction (where it’s pointing). For a point charge, the electric field \(\displaystyle\vec{E}\) at any point in space is given by the equation:

\(\displaystyle\vec{E} = \frac{1}{4\pi\epsilon_0} \cdot \frac{Q}{r^2} \cdot \hat{r}\)

• \(\displaystyle\frac{1}{4\pi\epsilon_0} \) is a constant that comes from Coulomb’s law, which helps us calculate the force between two charges. It’s called Coulomb’s constant.
• (Q) is the charge of our point charge. It’s the source of the electric field.
• (r) is the distance from the charge (Q) to the point where we’re measuring the electric field.
• \(\displaystyle\hat{r}\) is a unit vector that points from the charge (Q) directly to the point where we’re measuring the field.

Strength of the Electric Field:

The strength of the electric field gets weaker as you move away from the charge. Specifically, it decreases with the square of the distance from the charge—this is what the ( r² ) in the denominator tells us. The electric field has a specific direction associated with it. Understanding this direction is crucial for visualizing how charges interact. Here’s what you need to know:

The electric field is like an invisible force field that surrounds charged objects. It’s created by charges and influences other charges placed in its vicinity. Now, let’s dive into what makes the strength of the electric field important:

Definition: The electric field strength at any point is a measure of how strong the electric field is at that location. Imagine it as the intensity of the “push” or “pull” experienced by a tiny positive test charge placed there.

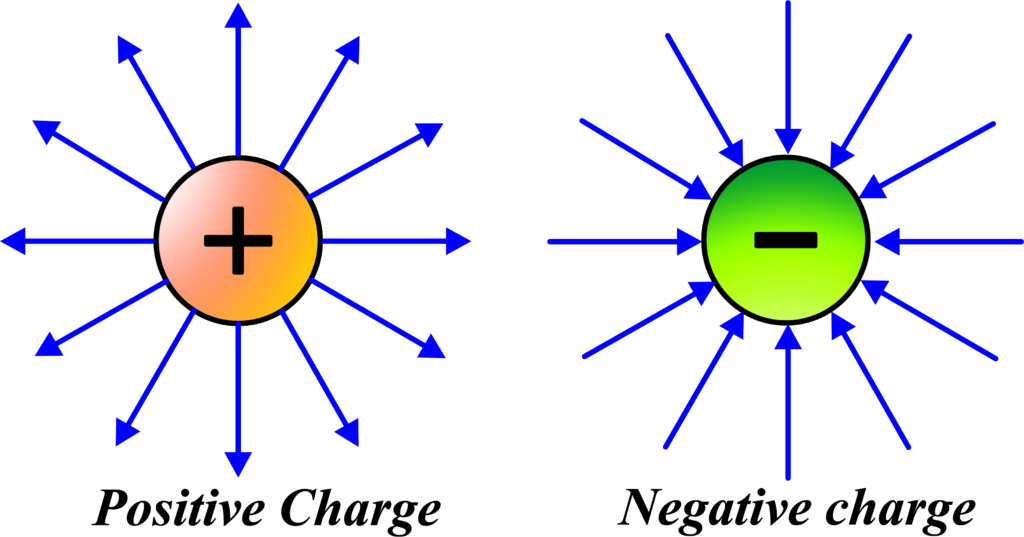
To understand the strength of the electric field, we use a positive test charge (let’s call it (q₀). When we place this test charge in an electric field, it experiences a force. The strength of the field is determined by how much force the test charge feels. The electric field strength is a vector quantity, meaning it has both magnitude (how strong) and direction. If the field is stronger, the force on the test charge will be greater. The direction of the field points away from positive charges and towards negative charges.

We can measure the strength of the electric field by dividing the force experienced by the test charge (F) by the magnitude of the test charge (q₀):

\(\displaystyle \text{Electric Field Strength} = \frac{F}{q_{0}} \)

The SI unit of electric field strength is Newton per coulomb (N/C). It tells us how many newtons of force a one-coulomb test charge would experience in that field. Electric field lines help us visualize the strength and direction of the field. They start with positive charges and end with negative charges. The density of these lines indicates the field’s strength: closer lines mean a stronger field.

Direction of the Electric Field:

The direction of the electric field is always radial. This means it points directly away from the charge if (Q) is positive, and directly towards the charge if (Q) is negative. The lines we draw to represent the electric field are called electric field lines, and they always start on positive charges and end on negative charges.

Definition: The electric field at any point represents the force experienced by a positive test charge placed at that point. It’s like a “map” of how other charges influence the space around them.

Imagine placing a tiny positive test charge at a specific location. The direction in which this test charge would move (if it were free to do so) gives us the direction of the electric field at that point.

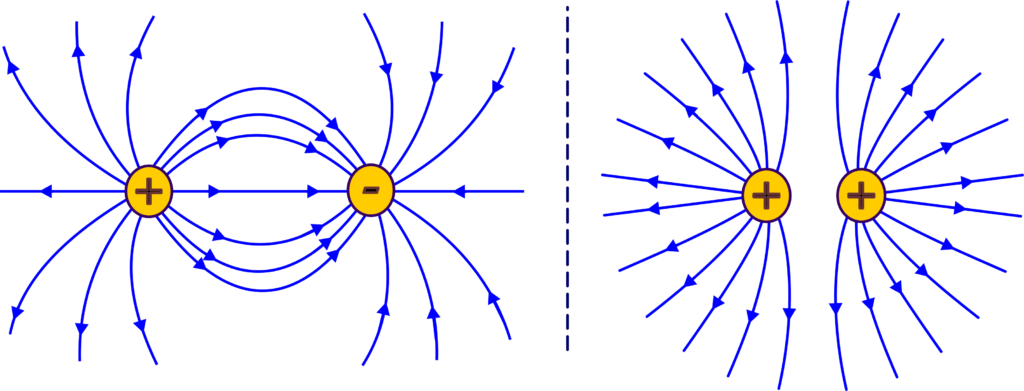
The electric field lines always point away from positive charges. So, if you have a positive charge, the electric field lines radiate outward from it. Conversely, the electric field lines point toward negative charges. Negative charges “pull” the electric field lines toward them.

Think of electric field lines as invisible paths that show how a positive test charge would move. They start on positive charges and end on negative charges. The density of these lines indicates the field’s strength: closer lines mean a stronger field. If you draw arrows along the field lines, they point in the direction of the electric field. These arrows help you visualize the field’s direction.

So, if you were a tiny positive test charge placed in the electric field of (Q), you would feel a force pushing you along the direction of the electric field lines. If you were negative, you’d feel the force pulling you in the opposite direction.

Derivation of Electric Field Due to a Point Charge

Imagine you have a point charge, (Q), which creates an electric field around it. We want to find out the strength and direction of this field at some distance (r) away from the charge.

Coulomb’s law tells us that the force (F) between two charges is proportional to the product of the charges and inversely proportional to the square of the distance between them:

\(\displaystyle F = k \cdot \frac{|Q_1 \cdot Q_2|}{r^2}\)

where (k) is Coulomb’s constant and (r) is the distance between the charges.

The electric field at a point in space is defined as the force per unit charge experienced by a small positive test charge (q₀) placed at that point:

\(\displaystyle \vec{E} = \frac{\vec{F}}{q_{0}}\)

If we place a small test charge (q₀) in the field created by (Q), the force on (q₀) according to Coulomb’s law is:

\(\displaystyle F = k \cdot \frac{|Q \cdot q_0|}{r^2} \)

Now, we substitute this force into the definition of the electric field:

\(\displaystyle\vec{E} = \frac{k \cdot \frac{|Q \cdot q_0|}{r^2}}{q_0}\)

The (q0) cancels out, leaving us with:

\(\displaystyle\vec{E} = k \cdot \frac{|Q|}{r^2}\)

The direction of the electric field is given by the unit vector (\(\displaystyle\hat{r}\)), which points away from the charge if (Q) is positive and towards the charge if (Q) is negative. So, we multiply our expression by (\(\displaystyle\hat{r} \)) to get the vector form:

\(\displaystyle\vec{E} = k \cdot \frac{|Q|}{r^2} \cdot \hat{r}\)

Coulomb’s constant (k) can be expressed in terms of the permittivity of free space (\(\displaystyle\epsilon_0\)):

\(\displaystyle k = \frac{1}{4\pi\epsilon_0}\)

Substituting this into our expression for (\(\displaystyle\vec{E} \)), we get the final formula:

\(\displaystyle \vec{E} = \frac{1}{4\pi\epsilon_0} \cdot \frac{Q}{r^2} \cdot \hat{r}\)

This is the expression for the electric field due to a point charge. It tells us that the electric field strength decreases with the square of the distance from the charge and that the field points radially away from a positive charge and towards a negative charge.

Also Read: Electric Field

Force Exerted by a Charge (Q) on a Test Charge

The electric force is what one charged object exerts on another. According to Coulomb’s law, the magnitude of this force is directly proportional to the product of the charges and inversely proportional to the square of the distance between them.

Coulomb’s law can be written as:

\(\displaystyle F = k \cdot \frac{|Q \cdot q_{0}|}{r^2} \)

• (F) is the magnitude of the force.
• (Q) and (q₀) are the charges.
• (r) is the distance between the charges.
• (k) is Coulomb’s constant, \(\displaystyle k = \frac{1}{4\pi\varepsilon_0} \), with \(\displaystyle\varepsilon_0\) being the permittivity of free space.

Since force is a vector quantity, it has both magnitude and direction. The direction of the force is along the line joining the charges and is given by the unit vector \(\displaystyle\hat{r} \).

• If (Q) is positive and (q₀) is positive, the force is repulsive, and \(\displaystyle\hat{r} \) points away from (Q).
• If one of the charges is negative, the force is attractive, and \(\displaystyle\hat{r}\) points towards (Q).

Now, we combine the magnitude from Coulomb’s law with the direction given by \(\displaystyle\hat{r} \) to express the force as a vector:

\(\displaystyle \vec{F} = \frac{1}{4\pi\varepsilon_{0}} \cdot \frac{Qq_{0}}{r^2} \cdot \hat{r}\)

This is the vector form of the force exerted by a charge (Q) on a charge (q₀), where \(\displaystyle\vec{F} \) points in the direction of \(\displaystyle\hat{r} \).

And that’s how you derive the expression for the force between two point charges. Students need to remember that the force is a vector, which means it has both a size (how strong it is) and a direction (where it’s going). This concept is fundamental in understanding how charges interact with each other and is a key part of the study of electrostatics.

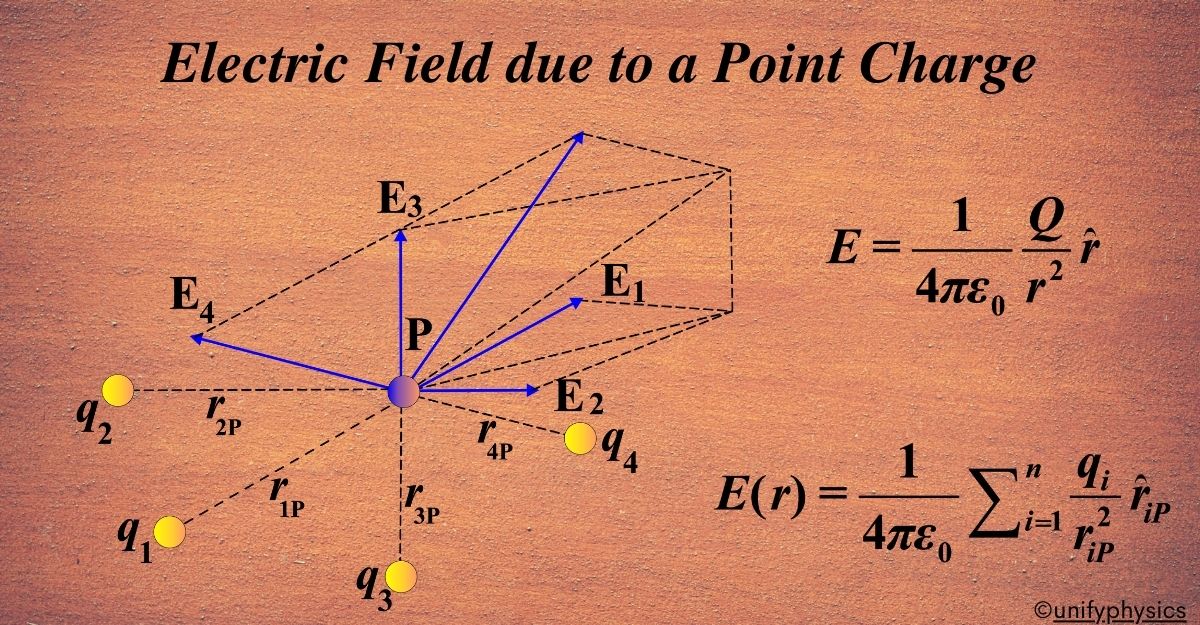
Electric Field Due to a System of Charges

When we have more than one charge, we can’t just consider them in isolation. Each charge creates its electric field, and when you put them together, these fields combine to form a new pattern. This is where the principle of superposition comes in handy.

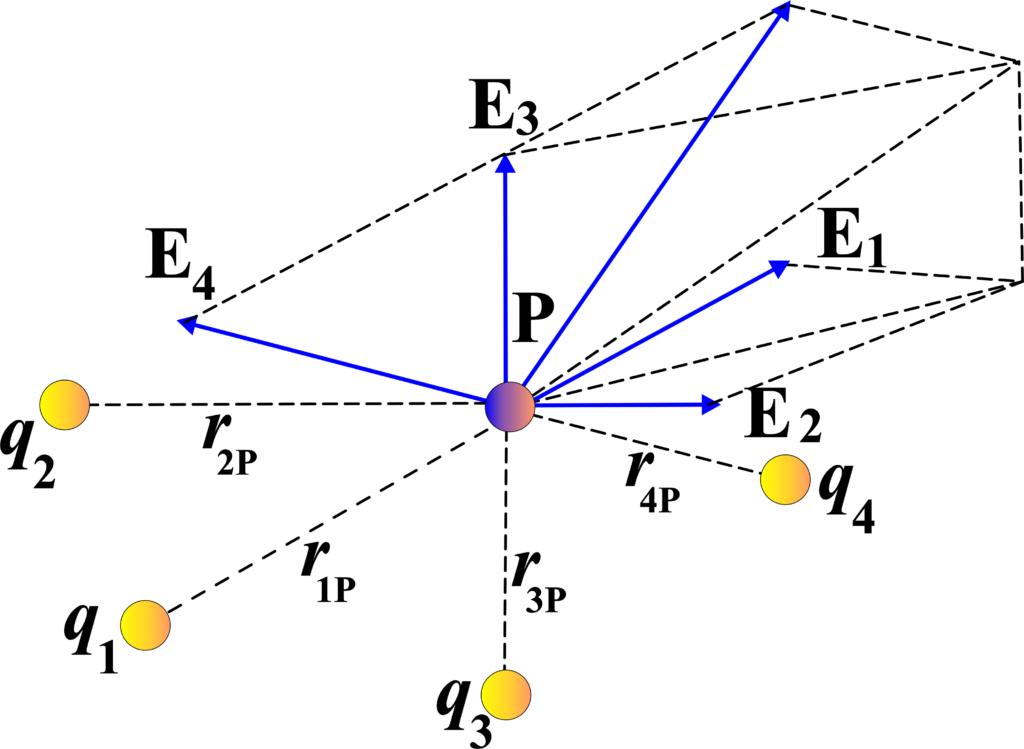
Principle of Superposition: The principle of superposition states that the total electric field created by a system of charges is the vector sum of the electric fields produced by each charge. This means we can calculate the electric field from each charge separately and then add them up to get the total field.

When we have multiple charges arranged in space, they collectively create an electric field at any point in that space. This field represents the influence of all the charges on a test charge placed at that point. Here’s how we express it:

Consider a system of charges \(\displaystyle q_1, q_2, \ldots, q_n \) located at different positions with respect to some origin (O). Each charge has a position vector \(\displaystyle\mathbf{r}_i \) pointing from the origin to that charge.

We want to find the electric field at a specific point (P) represented by the position vector \(\displaystyle\mathbf{r}\). Imagine placing a tiny positive test charge at (P) without disturbing the original positions of the charges.

The electric field at (P) due to the entire system of charges is the vector sum of the electric fields created by each charge. Mathematically, we write:

\(\displaystyle\mathbf{E}(r) = \mathbf{E}_1(r) + \mathbf{E}_2(r) + \ldots + \mathbf{E}_n(r)\)

• \(\displaystyle\mathbf{E}_i(r)\) is the electric field created by charge (q_i) at point (P).
• (r) represents the distance from the charge to point (P).
• The summation includes all charges in the system.

The electric field \(\displaystyle\mathbf{E}_i(r) \) due to a single charge (q_i) at point (P) is given by Coulomb’s law:

\(\displaystyle\mathbf{E}i(r) = \frac{1}{4\pi\varepsilon_{0}} \cdot \frac{q_{i}}{r{iP}^2} \cdot \hat{\mathbf{r}}_{iP}\)

• \(\displaystyle\varepsilon_0 \) is the permittivity of free space.
• (\(\displaystyle r_{iP} \)) is the distance from charge (q_i) to point (P).
• \(\displaystyle\hat{\mathbf{r}}_{iP} \) is the unit vector pointing from charge (q_i) to point (P).

The total electric field at point (P) is obtained by adding up the contributions from all charges:

\(\displaystyle\mathbf{E}(r) = \frac{1}{4\pi\varepsilon_0} \sum_{i=1}^{n} \frac{q_i}{r_{iP}^2} \cdot\hat{\mathbf{r}}_{iP}\)

This expression accounts for both the magnitudes and directions of the individual electric fields.

Physical Significance of the Electric Field

The electric field is a fundamental concept in physics that describes the influence a charge exerts on the space around it. Here’s what makes it so important:

• Invisible Influence: An electric field is like an invisible hand that can push or pull on charges without anything physically touching it. It’s a field that surrounds charged particles and affects other charged particles within that field, either attracting or repelling them.
• Force Carrier: The electric field acts as a carrier of force. If you place a positive test charge in an electric field, it will experience a force. This force is the physical manifestation of the electric field at that point in space.
• Vector Field: Since force is a vector quantity, the electric field is also a vector field. This means it has both magnitude (how strong it is) and direction (where it’s pointing). The direction of the electric field is always away from positive charges and towards negative charges.
• Atomic Scale: On the atomic scale, the electric field is the attractive force that holds the atomic nucleus and electrons together in atoms. It’s also responsible for the chemical bonding of atoms to form molecules.
• Energy Transport: Electric fields are involved in the transport of energy. For example, when charges move, they can create time-dependent electric fields that carry energy through space in the form of electromagnetic waves.
• Independent Entity: Although we can’t see electric fields, they are considered real physical entities. They have their dynamics and can exist independently of charges. They can also carry energy, which means they play a crucial role in the transmission of signals and energy.

Solved Examples

Example 1: Calculate the electric field at a point 0.5 meters away from a charge of (5 × 10^-6) C.

Solution: The electric field (E) due to a point charge is given by the formula:

\(\displaystyle E = \frac{kQ}{r^2} \)

• (k) is Coulomb’s constant (\(\displaystyle 8.99 \times 10^9 \, \text{N m}^2/\text{C}^2\)),
• (Q) is the charge (\(\displaystyle 5 \times 10^{-6} \, \text{C}\)),
• (r) is the distance from the charge (0.5 meters).

Substituting the values:

\(\displaystyle E = \frac{8.99 \times 10^9 \times 5 \times 10^{-6}}{(0.5)^2} \)
\(\displaystyle E = \frac{8.99 \times 10^9 \times 5 \times 10^{-6}}{0.25} \)
\(\displaystyle E = \frac{44.95 \times 10^3}{0.25} \)
\(\displaystyle E = 1.798 \times 10^5 \, \text{N/C} \)

Example 2: A charge of (3 × 10^-6) C is placed in an electric field of (2 × 10⁴ N/C). Calculate the force exerted on the charge.

Solution: The force (F) exerted on a charge in an electric field is given by:

\(\displaystyle F = qE \)

• (q) is the charge (\(\displaystyle 3 \times 10^{-6} \, \text{C}\)),
• (E) is the electric field (\(\displaystyle 2 \times 10^4 \, \text{N/C}\)).

Substituting the values:

\(\displaystyle F = 3 \times 10^{-6} \times 2 \times 10^4 \)
\(\displaystyle F = 6 \times 10^{-2} \, \text{N} \)

Example 3: Two charges, (+2 × 10^-6) C and (-2 × 10^-6) C, are placed 1 meter apart. Calculate the electric field at the midpoint between the charges.

Solution: The electric field due to a point charge at a distance (r) is given by:

\(\displaystyle E = \frac{kQ}{r^2} \)

At the midpoint, the distance from each charge to the point is 0.5 meters. For the positive charge:

\(\displaystyle E_1 = \frac{8.99 \times 10^9 \times 2 \times 10^{-6}}{(0.5)^2} \)
\(\displaystyle E_1 = \frac{8.99 \times 10^9 \times 2 \times 10^{-6}}{0.25} \)
\(\displaystyle E_1 = 7.192 \times 10^4 \, \text{N/C} \)

For the negative charge (in the opposite direction):

\(\displaystyle E_2 = \frac{8.99 \times 10^9 \times 2 \times 10^{-6}}{(0.5)^2} \)
\(\displaystyle E_2 = 7.192 \times 10^4 \, \text{N/C} \)

The fields due to the charges are equal in magnitude but opposite in direction, so they add up:

\(\displaystyle E = E_1 + E_2 \)
\(\displaystyle E = 7.192 \times 10^4 + 7.192 \times 10^4 \)
\(\displaystyle E = 1.4384 \times 10^5 \, \text{N/C} \)

Example 4: Calculate the electric field at a point 0.3 meters from a charge of (+1 × 10^-6) C and 0.4 meters from a charge of (-2 × 10^-6) C, both charges are along the x-axis.

Solution: Calculate the electric field due to each charge and then use vector addition.

For (+1 × 10^-6 C) :

\(\displaystyle E_1 = \frac{8.99 \times 10^9 \times 1 \times 10^{-6}}{(0.3)^2} \)
\(\displaystyle E_1 = \frac{8.99 \times 10^9 \times 1 \times 10^{-6}}{0.09} \)
\(\displaystyle E_1 = 9.99 \times 10^4 \, \text{N/C} \)

For (-2 × 10^-6 C) :

\(\displaystyle E_2 = \frac{8.99 \times 10^9 \times 2 \times 10^{-6}}{(0.4)^2} \)
\(\displaystyle E_2 = \frac{8.99 \times 10^9 \times 2 \times 10^{-6}}{0.16} \)
\(\displaystyle E_2 = 1.12375 \times 10^5 \, \text{N/C} \)

Since the charges are opposite, the fields are in opposite directions:

\(\displaystyle E_{total} = E_2 – E_1 \)
\(\displaystyle E_{total} = 1.12375 \times 10^5 – 9.99 \times 10^4 \)
\(\displaystyle E_{total} = 1.2475 \times 10^4 \, \text{N/C} \)

Example 5: Determine the distance from a point charge of (4 × 10^-6) C where the electric field strength is (1.8 × 10⁴ N/C).

Solution: Use the formula;

\(\displaystyle E = \frac{kQ}{r^2} \)

Rearrange to solve for (r):

\(\displaystyle r = \sqrt{\frac{kQ}{E}} \)

Substitute the values:

\(\displaystyle r = \sqrt{\frac{8.99 \times 10^9 \times 4 \times 10^{-6}}{1.8 \times 10^4}} \)
\(\displaystyle r = \sqrt{\frac{3.596 \times 10^4}{1.8 \times 10^4}} \)
\(\displaystyle r = \sqrt{2} \)
\(\displaystyle r \approx 1.414 \, \text{m} \)

FAQs