The story of electric potential began long before the term itself was coined. In the 17th century, pioneers like Otto von Guericke, William Gilbert, and Robert Boyle laid the groundwork by studying electricity and its various properties. Their experiments and observations were crucial in setting the stage for later developments.
It wasn’t until the 18th century that the concept of electric potential started to take shape. This was a period marked by rapid progress in the field of electricity. Scientists were beginning to understand that there was a “force” associated with electric charges, but they didn’t yet have the language or the mathematics to describe it precisely.
The term “electric potential” would come into clearer focus thanks to Alessandro Volta, an Italian physicist whose name is now synonymous with electrical potential (and the unit ‘volt’). Volta’s work in the late 18th and early 19th centuries was instrumental. He derived the concept of electrical potential from his studies of static electricity and went on to discover the principle of the battery through his experiments with dissimilar metals in contact with moisture. This invention not only provided a steady source of electrical energy but also led to a deeper understanding of electric potential differences.
In honor of Volta’s contributions, the unit of electric potential was named the volt. This unit helps us measure the potential difference, which is essentially the work needed to move a unit charge from one point to another against an electric field.
The concept of electric potential has evolved over the centuries, and today it is a fundamental aspect of not just physics, but all electrical engineering and technology. It’s a testament to the curiosity and ingenuity of scientists who, over the years, have built upon each other’s work to advance our understanding of the natural world.
What is Electric Potential?
The electric potential at a point is the amount of electric potential energy that a unit positive charge would have at that point. It’s like the electrical “height” from which a charge can “fall”. The higher the electric potential, the more potential energy per charge.
Imagine you’re at a water park, standing at the top of a water slide. The higher you are, the more potential energy you have due to gravity. Now, let’s swap the water park for an electric field, and instead of you, we have a positive charge. The Electric Potential at any point in this electric field is like the height of the water slide—it tells us how much potential energy a positive charge has just because of its position.
Electric potential is measured in volts (V), and one volt is defined as the potential difference that will move one coulomb of charge with one joule of energy. In simpler terms, it’s the electric “pressure” that can push electrons through a circuit.
To understand this better, let’s go back to our water park analogy. The height of the water slide represents the electric potential, and the water flowing down is like the charges moving through a wire. Just as water naturally flows from high to low height, electric charges flow from high to low potential.
Mathematically, we express electric potential (V) as the work done (W) per unit charge (q) to move a charge from a reference point (usually infinity) to the point in question:
\(\displaystyle V = \frac{W}{q} \)
It’s important to note that electric potential is related to potential energy (U).
Electric Potential and Potential Energy
The electric potential at a point in space is defined as the amount of work done in bringing a unit positive charge from infinity to that point. It’s like the “electric altitude” at which a charge sits. The higher the electric potential, the more “electric height” a charge has.
Potential energy, on the other hand, is the energy that a charge possesses due to its position in an electric field. It’s like the energy you have when you’re at the top of a slide—the higher you are, the more potential energy you have.
The relationship between electric potential (V) and potential energy (U) is quite direct. The potential energy of a charge (q) at a point with electric potential (V) is given by:
\(\displaystyle U = qV \)
This equation tells us that the potential energy is the product of the charge and the electric potential at that point.
Think of electric potential as the price per apple (where apples are charged), and potential energy as the total cost for a bag of apples. The more apples you have (charge (q), or the higher the price per apple (electric potential (V), the more you’ll have to pay (potential energy (U).
Understanding this relationship is crucial because it helps us predict how a charge will behave in an electric field. A charge in a high potential area (like the top of the slide) has a lot of potential energy and can do work as it moves to a lower potential area (like sliding down).
If you have a positive charge near a positive source charge, it has high potential energy because it’s in a high electric potential region. If it’s allowed to move, it will “fall” towards a region of lower potential, converting potential energy into kinetic energy, much like a ball rolling down a hill.
Characteristics of Electric Potential
Scalar Quantity: Electric potential is a scalar quantity. This means it has magnitude but no direction. Unlike vectors, which have both magnitude and direction, scalar quantities like electric potential can be added together directly without considering angles or directions.
Measured in Volts: The unit of electric potential is the volt (V). One volt is defined as the potential difference that moves one coulomb of charge with one joule of energy. It’s like the “electric height” measured in “electric meters”.
Positive or Negative: An electric potential can be positive or negative, depending on the type of charge creating the potential. A point near a positive charge has a positive electric potential, while a point near a negative charge has a negative electric potential.
Zero at Infinity: The electric potential is considered to be zero at infinity. This is a reference point used to measure electric potential at other points in space. It’s like saying the sea level is the reference point for measuring the height of mountains.
Depends on Distance: Electric potential depends on the distance from the source charge. The closer you are to the charge, the higher the electric potential. It’s similar to how the loudness of sound depends on how close you are to the source of the sound.
Independent of Path: Since the electric potential is related to electric potential energy, which is a conservative force, the electric potential at a point does not depend on the path taken to reach that point. It’s like the amount of work done in lifting an object to a certain height doesn’t depend on the path taken.
Equipotential Surfaces: Points that have the same electric potential form an equipotential surface. No work is done when moving a charge along an equipotential surface because the electric potential is the same throughout the surface.
Perpendicular to Electric Field Lines: Equipotential surfaces are always perpendicular to electric field lines. This is because work is only done when moving charges along the direction of the electric field, not across it.
Remember, each characteristic gives us insight into the invisible but crucial “landscape” of electric forces that govern the behavior of charged particles.
Electric Potential Due to Point Charge
Electric potential is the work done to move a unit of positive charge from infinity to a point in an electric field without any acceleration. It’s like measuring how much effort it takes to bring a ball uphill from the ground.
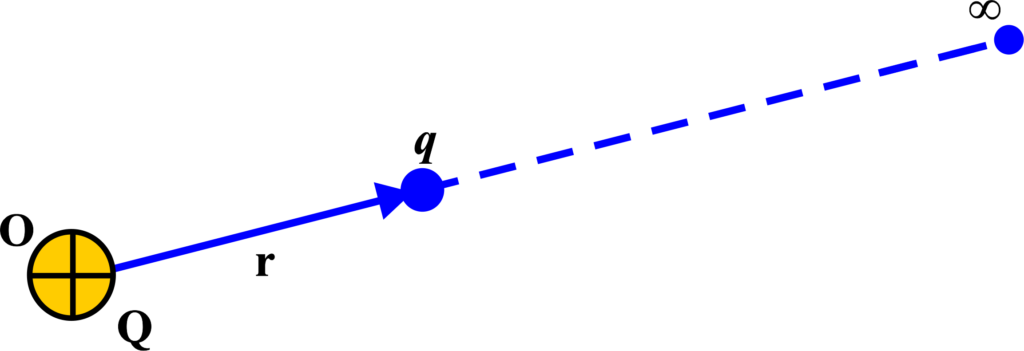
We start with the concept of work done (W) by an external force to bring a charge (q) from infinity to a point in the field of another stationary charge (Q).
The work done against the electric field to move the charge (q) from infinity to a point at a distance (r) from (Q) is given by:
\(\displaystyle W = \int_{\infty}^{r} F \, dr \)
The force (F) at a distance (r) due to the electric field (E) created by the charge (Q) is:
\(\displaystyle F = qE \)
The electric field (E) due to a point charge (Q) at a distance (r) is:
\(\displaystyle E = \frac{kQ}{r^2} \)
where ( k ) is Coulomb’s constant. We get the force as a function of distance (r):
\(\displaystyle F = q \left( \frac{kQ}{r^2} \right) \)
Now, we integrate the force over the distance from infinity to (r):
\(\displaystyle W = \int_{\infty}^{r} q \left( \frac{kQ}{r^2} \right) dr \)
Performing the integration, we get:
\(\displaystyle W = -qkQ \left[ \frac{1}{r} \right]_{\infty}^{r} \)
Since ( \(\displaystyle\frac{1}{\infty} = 0 \)), the expression simplifies to:
\(\displaystyle W = \frac{qkQ}{r} \)
Finally, electric potential is defined as the work done per unit charge, so we divide the work done by (q):
\(\displaystyle V = \frac{W}{q} = \frac{kQ}{r} \)
This means that the potential is directly proportional to the charge (Q) and inversely proportional to the distance (r).
Significance of Coulomb’s constant (k) in this derivation?
Coulomb’s constant has a value of approximately (8.99 × 109) N·m²/C². This value is essential in calculating the force between two charges and, consequently, the electric potential.
The constant (k) comes from Coulomb’s Law, which states that the force (F) between two point charges is directly proportional to the product of their charges (q1) and (q2), and inversely proportional to the square of the distance (r) between them:
\(\displaystyle F = k \frac{q_1 q_2}{r^2} \)
The constant (k) quantifies the strength of the electrostatic force. A larger value of (k) means a stronger force for the same charges and distance. It’s a measure of how “strong” the electric field is in a vacuum. Just like the gravitational constant (G) in Newton’s law of gravitation, (k) is a universal constant in electrostatics. It allows us to use Coulomb’s Law universally for any two-point charges.
In the context of electric potential, (k) is used to determine the work done per unit charge (which is the electric potential (V)) in bringing a charge from infinity to a point in the field of another charge. The formula for electric potential due to a point charge (Q) is:
\(\displaystyle V = \frac{kQ}{r} \)
Here, (k) ensures that the units of electric potential are volts (V), which is joules per coulomb (J/C).
Coulomb’s constant acts as a scaling factor that adjusts the theoretical equations to match real-world measurements. Without (k), the calculated forces and potentials would not align with what we observe in experiments.
Electric Potential Due to System of Charges
When there are multiple charges, the total electric potential is the sum of the potentials due to individual charges. This is because electric potential is a scalar and can simply be added up.
Imagine you’re at a party and there are several balloons around you. Some balloons have positive charges, some have negative, and they all exert forces on each other. Now, if you want to bring in another charged balloon, you’ll need to consider the influence of all these existing balloons to figure out how much effort it’ll take to place your balloon at a particular spot.
The electric potential due to a system of charges is the cumulative effect of all individual charges in that system. It’s like adding up the influence of each balloon at the party to understand the total “party atmosphere” at any point.
The total electric potential at a point is the algebraic sum of the potentials due to each charge in the system. This is known as the Superposition Principle. It’s like adding up the loudness of each speaker in a room to get the total volume.
The formula for the electric potential (V) at a point due to a system of charges is:
\(\displaystyle V = k \sum \left( \frac{Q_i}{r_i} \right) \)
- (V) is the total electric potential at the point.
- (k) is Coulomb’s constant.
- (Qi) is the magnitude of the (ith) charge.
- (ri) is the distance from the (ith) charge to the point.
Consider a system consisting of multiple point charges (Q1, Q2, …, Qn) located at various points in space.
Each charge (Qi) creates an electric potential (Vi) at a point in space, which can be calculated using the formula for a single point charge:
\(\displaystyle V_i = \frac{kQ_i}{r_i} \)
where (ri) is the distance from the charge (Qi) to the point of interest, and (k) is Coulomb’s constant.
The total electric potential (V) at any point is the sum of the individual potentials created by each charge in the system. This is due to the superposition principle, which states that for linear forces, the net effect at a point is the sum of the effects produced by each source individually.
To find the total electric potential (V) at a point, we add up the potentials due to all the individual charges:
\(\displaystyle V = V_1 + V_2 + … + V_n \)
Substituting the individual potentials, we get:
\(\displaystyle V = \frac{kQ_1}{r_1} + \frac{kQ_2}{r_2} + … + \frac{kQ_n}{r_n} \)
Since (k) is a constant, we can factor it out of the summation:
\(\displaystyle V = k \left( \frac{Q_1}{r_1} + \frac{Q_2}{r_2} + … + \frac{Q_n}{r_n} \right) \)
The final expression for the electric potential due to a system of charges is:
\(\displaystyle V = k \sum_{i=1}^{n} \frac{Q_i}{r_i} \)
where the summation runs over all charges in the system. The electric potential at a point due to a system of charges is the algebraic sum of the potentials due to each charge. The formula takes into account the magnitude and sign of each charge, as well as the distance from each charge to the point of interest.
What Is Equipotential Surface?
An equipotential surface is a 3D surface in space where every point has the same electric potential. No work is required to move a charge along this surface.
Imagine you’re at a theme park with a map that shows areas of equal height above sea level. These areas are like “height-equal” zones. Now, let’s think of electric potential instead of height. An equipotential surface is like a “potential-equal” zone in an electric field. It’s a 3D surface where every point has the same electric potential value.
Think of a flat tabletop as an equipotential surface. If you had a ball on this table, you could roll it around without it suddenly rolling off or changing speed—it’s all level. Similarly, on an equipotential surface, a charge can move around without gaining or losing electric potential energy.
- No Work Required: Just like you don’t need to push the ball uphill on the tabletop, no work is needed to move a charge from one point to another on an equipotential surface.
- Perpendicular to Electric Field Lines: Equipotential surfaces are always perpendicular to electric field lines. This is because moving along the surface doesn’t change the potential, just like moving along the tabletop doesn’t change the height.
Examples:
- Around a Point Charge: For a single point charge, equipotential surfaces are spherical shells centered on the charge. It’s like having a set of nesting dolls, each representing a different potential level.
- In a Uniform Field: In a uniform electric field (like between two parallel plates), equipotential surfaces are flat planes parallel to the plates.
What happens when two charges are placed on the same equipotential surface?
When two charges are placed on the same equipotential surface, a few interesting things happen:
No Work Done: Since the potential is the same everywhere on an equipotential surface, moving a charge along it doesn’t involve changing its potential energy. Therefore, no work is done in moving a charge along an equipotential surface.
Potential Remains Constant: The electric potential at every point on the equipotential surface remains constant, even when multiple charges are present. This means that the charges do not work on each other when moved along the surface.
Field Distortion: The presence of the charges can distort the electric field in the surrounding space. When multiple, discrete charges interact, their fields overlap, resulting in a combining of potential, which can skew equipotential lines in areas close enough to both charges to “feel” the effects of both fields.
Charge Redistribution: If the charges are free to move (like in a conductor), they will redistribute themselves to maintain the equipotential condition. This redistribution occurs because charges will repel each other until they reach a state where the surface is again an equipotential.
So, placing two charges on the same equipotential surface doesn’t change the potential energy of the charges as long as they stay on that surface. However, their presence can affect the shape of the surrounding electric field and, if they are free to move, they will adjust their positions to maintain the equipotential nature of the surface.
Properties of Equipotential Surface
Perpendicular to Electric Field Lines: Equipotential surfaces are always perpendicular to electric field lines at every point. This is like saying the contour lines on a map, which represent points of equal elevation, are always perpendicular to the direction of the steepest slope.
Never Intersect Each Other: Just as contour lines on a map never cross each other, two equipotential surfaces can never intersect. If they did, it would mean that a single point in space could have two different potentials, which is impossible.
Concentric Spherical Shells for Point Charges: For a point charge, the equipotential surfaces are concentric spherical shells centered around the charge. It’s similar to layers of an onion, where each layer represents a different potential level.
Planes in a Uniform Field: In a uniform electric field, like the one between two parallel plates, the equipotential surfaces are flat planes perpendicular to the field lines. Think of it as floors in a building, where each floor represents a different potential level.
Direction from High to Low Potential: The direction of an equipotential surface is always from high potential to low potential. This is akin to water flowing downhill from a higher elevation to a lower elevation.
Constant Potential Inside a Conductor: Inside a hollow-charged spherical conductor, the potential is constant. This can be treated as an equipotential volume, meaning no work is required to move a charge from the center to the surface.
Spacing Indicates Field Strength: The spacing between equipotential surfaces can tell us about the strength of the electric field. Closer surfaces indicate a stronger field, and farther surfaces indicate a weaker field. This is because the rate at which potential changes with distance is related to the strength of the electric field.
Work Done in an Equipotential Surface
The electric potential is the same at all points on an equipotential surface, the work done in moving a charge on it is zero. This is because work is related to the change in potential energy, and if the potential is the same, there’s no change.
Imagine you’re in a flat park where the ground is perfectly level. You have a ball, and you start rolling it around. No matter where you roll it, it doesn’t go uphill or downhill—it stays on the same level. This park is like an equipotential surface, and the ball is like a charge.
On an equipotential surface, all points have the same electric potential. This means that if you move a charge anywhere on this surface, you’re not moving it to a place with more or less electric potential energy—it stays the same.
Because the electric potential is the same everywhere on this surface, moving a charge along it doesn’t involve changing its potential energy. Therefore, no work is done in moving a charge along an equipotential surface. The formula for work done (W) in moving a charge (q) in an electric field is:
\(\displaystyle W = q\Delta V \)
where (∆V) is the change in electric potential. Since (∆V = 0) on an equipotential surface, the work done is:
\(\displaystyle W = q(0) = 0 \)
This concept is important because it tells us that we can move charges around on these surfaces without expending any energy. It’s like being able to move the ball around the park without getting tired because the ground is level.
If we could see equipotential surfaces, they would look like invisible “shelves” in the air, each at a different height. But once you’re on one shelf, you can walk around freely without going up or down to another shelf.
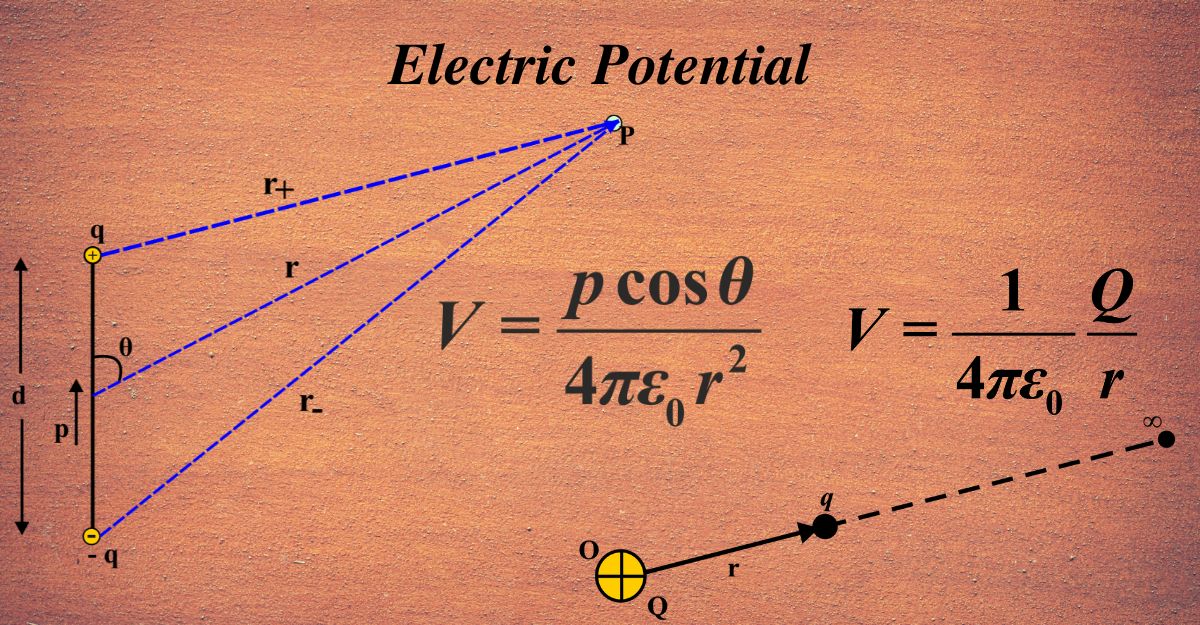
Electric Potential Due To A Dipole
A dipole consists of two equal and opposite charges, (+q) and (-q), separated by a distance (d). The electric potential due to a dipole is the work done to move a unit of positive charge from infinity to a point in the field created by the dipole.
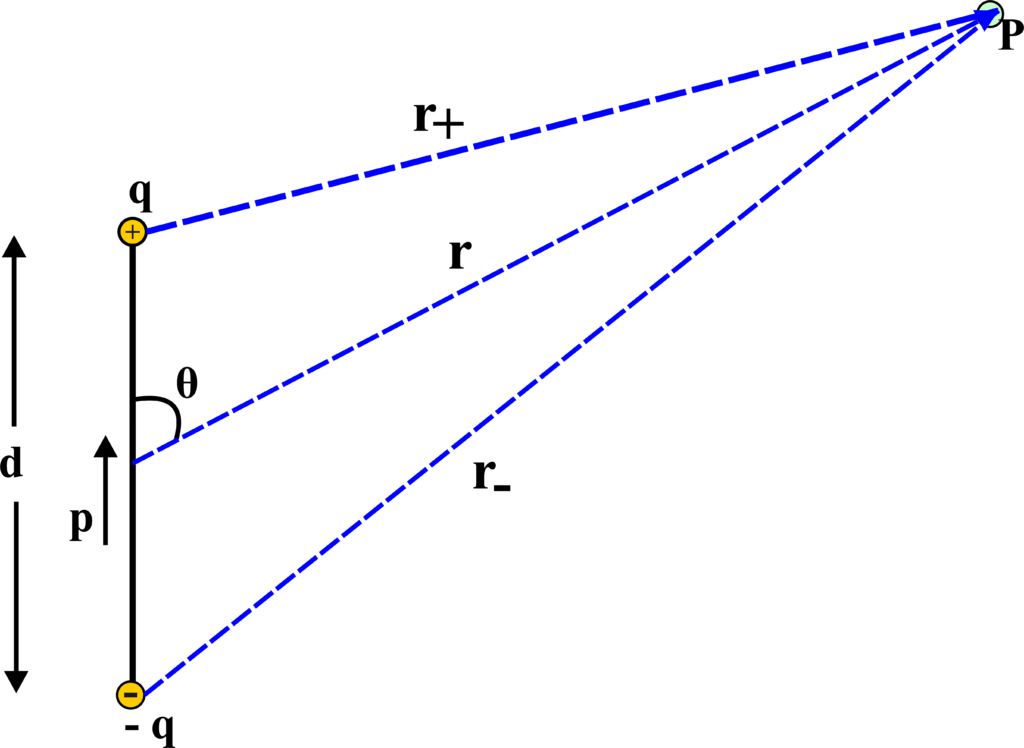
We want to find the potential at a point P, which is at a distance (r) from the center of the dipole and makes an angle (θ) with the dipole axis.
The potential due to the positive charge (+q) at point P is:
\(\displaystyle V_+ = \frac{kq}{r_+} \)
And the potential due to the negative charge (-q) at point P is:
\(\displaystyle V_- = -\frac{kq}{r_-} \)
where (r+) and (r–) are the distances from the charges to point P, and (k) is Coulomb’s constant. The total potential at point P due to both charges is the sum of the individual potentials:
\(\displaystyle V = V_+ + V_- \)
Substituting the individual potentials, we get:
\(\displaystyle V = \frac{kq}{r_+} – \frac{kq}{r_-} \)
If point P is far from the dipole, we can approximate (\(\displaystyle r_+ \approx r_- \approx r \)), where (r) is the distance from the dipole’s center to point P.
For small angles (θ), we can use the approximation:
\(\displaystyle r_- – r_+ \approx d \cos \theta \)
Substituting the approximations into the potential equation, we get:
\(\displaystyle V = \frac{kq(d \cos \theta)}{r^2} \)
Since the electric dipole moment (p) is defined as (p = qd), we can write:
\(\displaystyle V = \frac{kp \cos \theta}{r^2} \)
This formula shows that the potential depends on the dipole moment (p), the distance (r), and the angle (θ). It also tells us that the potential decreases with the square of the distance from the dipole.
Also Read: Electric Dipole
Solved Examples
Problem 1: Calculate the electric potential at a distance of (0.2 m) from a point charge (\(\displaystyle q = 5 \times 10^{-6} \ \text{C} \)).
Solution: The electric potential (V) due to a point charge (q) at a distance (r) is given by:
\(\displaystyle V = \frac{q}{4 \pi \epsilon_0 r} \)
Given: \(\displaystyle q = 5 \times 10^{-6} \ \text{C} \); r = 0.2 m ; \(\displaystyle \epsilon_0 = 8.85 \times 10^{-12} \ \text{C}^2/\text{N} \cdot \text{m}^2 \).
Substituting the values:
\(\displaystyle V = \frac{5 \times 10^{-6}}{4 \pi \times 8.85 \times 10^{-12} \times 0.2} \)
Calculating:
\(\displaystyle V = \frac{5 \times 10^{-6}}{2.22 \times 10^{-11}} \)
\(\displaystyle V \approx 2.25 \times 10^{5} \ \text{V} \)
Problem 2: Calculate the electric potential at a point (P) due to two charges (\(\displaystyle q_1 = 3 \times 10^{-6} \ \text{C} \)) and (\(\displaystyle q_2 = -2 \times 10^{-6} \ \text{C} \)) placed 0.1 m apart. Point (P) is located 0.05 m from (q1) and 0.15 m from (q2).
Solution: The electric potential at point (P) due to multiple charges is the sum of potentials due to individual charges:
\(\displaystyle V = V_1 + V_2 \)
Where:\(\displaystyle V_1 = \frac{q_1}{4 \pi \epsilon_0 r_1} \) ; \(\displaystyle V_2 = \frac{q_2}{4 \pi \epsilon_0 r_2} \)
Substituting the values:
\(\displaystyle V_1 = \frac{3 \times 10^{-6}}{4 \pi \times 8.85 \times 10^{-12} \times 0.05} \)
\(\displaystyle V_2 = \frac{-2 \times 10^{-6}}{4 \pi \times 8.85 \times 10^{-12} \times 0.15} \)
Calculating:
\(\displaystyle V_1 = \frac{3 \times 10^{-6}}{5.54 \times 10^{-13}} \approx 5.41 \times 10^{6} \ \text{V}\)
\(\displaystyle V_2 = \frac{-2 \times 10^{-6}}{1.66 \times 10^{-12}} \approx -1.20 \times 10^{6} \ \text{V} \)
So,
\(\displaystyle V = 5.41 \times 10^{4} \ \text{V} + (-1.20 \times 10^{4} \ \text{V})\)
\(\displaystyle V \approx 4.21 \times 10^{4} \ \text{V} \)
Problem 3: Calculate the electric potential at a point (P) on the axial line of an electric dipole with dipole moment (\(\displaystyle p = 2 \times 10^{-29} \ \text{Cm} \)) at a distance (r = 0.1 m) from the center of the dipole.
Solution: The electric potential (V) due to a dipole at a point on its axial line is given by:
\(\displaystyle V = \frac{p}{4 \pi \epsilon_0 r^2} \)
Substituting the values:
\(\displaystyle V = \frac{2 \times 10^{-29}}{4 \pi \times 8.85 \times 10^{-12} \times (0.1)^2}\)
Calculating:
\(\displaystyle V = \frac{2 \times 10^{-29}}{1.11 \times 10^{-12}}\)
\(\displaystyle V \approx 1.80 \times 10^{-17} \ \text{V} \)
Problem 4: Calculate the electric potential energy of a system of two charges (\(\displaystyle q_1 = 3 \times 10^{-6} \ \text{C} \)) and (\(\displaystyle q_2 = -2 \times 10^{-6} \ \text{C} \)) separated by a distance (r = 0.1 m).
Solution: The electric potential energy (U) of a system of two-point charges is given by:
\(\displaystyle U = \frac{q_1 q_2}{4 \pi \epsilon_0 r} \)
Substituting the values:
\(\displaystyle U = \frac{(3 \times 10^{-6})(-2 \times 10^{-6})}{4 \pi \times 8.85 \times 10^{-12} \times 0.1} \)
Calculating:
\(\displaystyle U = \frac{-6 \times 10^{-12}}{1.11 \times 10^{-11}} \)
\(\displaystyle U \approx -0.54 \ \text{J} \)
Problem 5: A dipole with dipole moment (\(\displaystyle p = 2 \times 10^{-29} \ \text{Cm} \)) is placed in a uniform electric field (\(\displaystyle E = 1 \times 10^{5} \ \text{N/C} \)). Calculate the potential energy when the dipole is aligned parallel to the electric field.
Solution: The potential energy (U) of a dipole in a uniform electric field is given by:
\(\displaystyle U = – p E \cos \theta \)
For parallel alignment, (θ = 0∘) and ( cos 0 = 1 ).
Given:
\(\displaystyle p = 2 \times 10^{-29} \ \text{Cm} \)
\(\displaystyle E = 1 \times 10^{5} \ \text{N/C} \)
Substituting the values:
\(\displaystyle U = – (2 \times 10^{-29}) (1 \times 10^{5}) \)
\(\displaystyle U = -2 \times 10^{-24} \ \text{J} \)
FAQs
Q1: What is electric potential?
Electric potential at a point in an electric field is the amount of work done in bringing a unit positive charge from infinity to that point without any acceleration. It is a measure of the potential energy per unit charge at that point.
How is electric potential different from electric potential energy?
Electric potential is the potential energy per unit charge at a specific point in an electric field. In contrast, electric potential energy is the total energy a charge possesses due to its position in the electric field. The potential is a property of the field, while potential energy is a property of the charge in the field.
What is an equipotential surface?
An equipotential surface is a surface on which every point has the same electric potential. No work is required to move a charge along this surface because the potential difference between any two points on the surface is zero.
How are electric field lines oriented with respect to equipotential surfaces?
Electric field lines are always perpendicular to equipotential surfaces. This perpendicular orientation ensures that no work is done when moving a charge along an equipotential surface.
Can equipotential surfaces intersect each other? Why or why not?
Equipotential surfaces cannot intersect each other because each point in space can only have one electric potential value. If they were to intersect, it would imply that a point has two different potential values simultaneously, which is impossible.
How does the shape of equipotential surfaces differ for various charge configurations?
For a point charge, equipotential surfaces are concentric spheres centered around the charge. For a uniform electric field, they are parallel planes perpendicular to the field lines. For a dipole, they are more complex, forming shapes that reflect the influence of both charges.
What is the significance of closely spaced equipotential surfaces?
Closely spaced equipotential surfaces indicate a strong electric field. The closer the surfaces are to each other, the greater the potential gradient and the stronger the electric field in that region.