Electromagnetic Waves

The story of electromagnetic waves begins with the brilliant Scottish physicist James Clerk Maxwell. In the mid-19th century, Maxwell was the first to predict the existence of electromagnetic waves. He did this by combining the laws of electricity and magnetism into a set of equations that bear his name—Maxwell’s Equations. These equations suggested that electric and magnetic fields could travel through space as waves.

Following Maxwell’s theoretical predictions, it was the German physicist Heinrich Hertz who, in 1887, successfully produced and detected electromagnetic waves in the laboratory. He used a spark gap transmitter to create waves with a wavelength of about 6 meters. Hertz’s experiments confirmed Maxwell’s theory and paved the way for the practical use of electromagnetic waves.

The late 19th and early 20th centuries saw rapid advancements in the understanding and application of electromagnetic waves. An Indian scientist, Jagadish Chandra Bose, extended Hertz’s work and produced electromagnetic waves with much shorter wavelengths, ranging from 5 mm to 25 mm. His contributions were significant in the development of wireless communication.

The Italian inventor Guglielmo Marconi took the next giant leap. He was the first to demonstrate the feasibility of wireless communication over long distances. Marconi discovered that by connecting one terminal of the spark gap transmitter to an antenna and grounding the other, he could send electromagnetic waves several kilometers away. This breakthrough led to the development of radio technology as we know it today.

What are Electromagnetic Waves?

electromagnetic waves are invisible energy waves created by vibrating electric charges, capable of traveling through space at the speed of light. Electromagnetic waves are energy waves created when an electric field pairs with a magnetic field. They are transverse waves, meaning the electric and magnetic fields are perpendicular to the direction of wave propagation.

Imagine you drop a pebble into a still pond. You see ripples spreading out in circles – these are similar to waves, but they happen in water. Now, let’s think about something similar happening in the air, but instead of water, we have electric and magnetic fields creating the ripples.

Electromagnetic waves are like invisible ripples that travel through space. They are created when an electric charge, like an electron, moves back and forth. This moving charge creates a changing electric field, which then creates a changing magnetic field, and this process continues. The result is a wave that travels outward in all directions.

These waves are special because they don’t need anything like air or water to travel through; they can move through the vacuum of space. That’s how the light from the sun gets to us on Earth!

The electric and magnetic fields in an electromagnetic wave are perpendicular to each other, and they are also perpendicular to the direction the wave is moving. This is why we call them transverse waves.

Electromagnetic waves come in many types, depending on their frequency and wavelength. The types include radio waves, microwaves, infrared, visible light (which we can see), ultraviolet, X-rays, and gamma rays.

How Are Electromagnetic Waves Formed?

electromagnetic waves are formed by the movement of electric charges, which create oscillating electric and magnetic fields that spread out at the speed of light. It’s like a cosmic dance that happens all around us, invisible to the naked eye but essential to the way we live our lives. This vibration creates a wave that is both electric and magnetic.

To understand how electromagnetic waves are formed, let’s start with something familiar: a light bulb. When you turn on a light bulb, it emits light that travels to your eyes, allowing you to see. But what’s happening on a level we can’t see?

It all begins with an electric charge. This could be a tiny particle like an electron. When this charge moves, it creates an electric field around it. Now, if the charge moves back and forth quickly, this electric field changes rapidly too.

Here’s where it gets interesting. According to physics, a changing electric field produces a magnetic field. So, as our electric charge dances back and forth, it’s not just creating an electric field; it’s also creating a magnetic field.

These two fields – electric and magnetic – are interconnected. As the electric field changes, it generates a magnetic field, and as the magnetic field changes, it generates an electric field. This interplay creates a self-sustaining wave that travels through space.

This wave of energy, made up of oscillating electric and magnetic fields, is what we call an electromagnetic wave. The wave moves outward in all directions from the source, much like ripples in a pond.

And here’s the most amazing part: these waves travel at the speed of light, which is about 300,000 kilometers per second in a vacuum. That’s why, when you flip the light switch, the room lights up almost instantly!

Electromagnetic waves aren’t just light, though. They include a wide range of energies, from low-energy radio waves to high-energy gamma rays. All of these waves are formed in the same basic way, with a moving charge and the resulting dance of electric and magnetic fields.

Nature of Electromagnetic Waves

When we talk about the nature of electromagnetic waves, we’re referring to how they behave and what they’re made of. Electromagnetic waves are fascinating because they are a combination of electric and magnetic fields that travel through space.

Transverse waves are waves where the oscillations are perpendicular to the direction the wave is traveling. For electromagnetic waves, this means that the electric field and magnetic field are oscillating in directions that are at right angles to the direction in which the wave is moving.

Imagine you’re holding a rope and you flick it up and down. The wave that travels along the rope moves horizontally, but the rope itself moves up and down. That’s what we mean by transverse – the movement of the fields is perpendicular to the direction of the wave’s travel.

In an electromagnetic wave:

• The electric field (\(\displaystyle\vec{E} \)) is a force field that surrounds electric charges and exerts a force on other charges within the field.
• The magnetic field (\(\displaystyle\vec{B}\)) is similar but is produced by moving charges (like electrons) and exerts a force on other moving charges or magnetic materials.

These two fields are not just perpendicular to each other; they are also in phase, meaning they reach their maximum and minimum points together as they travel through space.

Another key aspect of electromagnetic waves is that they don’t need a medium to travel through. Unlike sound waves, which need air or another material to move, electromagnetic waves can travel through the vacuum of space. This is why we can receive sunlight and other cosmic signals from across the universe.

The nature of electromagnetic waves also defines the electromagnetic spectrum, which includes radio waves, microwaves, infrared, visible light, ultraviolet, X-rays, and gamma rays. Each type of wave has a different wavelength and frequency, but they all share the transverse, oscillating nature of electromagnetic waves.

Mathematical Representation of Electromagnetic Wave

When we talk about electromagnetic waves mathematically, we’re looking at equations that describe how these waves behave. It’s like having a secret code that tells us everything about the wave – how strong it is, how fast it’s moving, and what direction it’s going in.

To describe an electromagnetic wave, we need to know about its electric field (E) and its magnetic field (B). These fields are vectors, which means they have both a magnitude (how strong they are) and a direction (where they’re pointing).

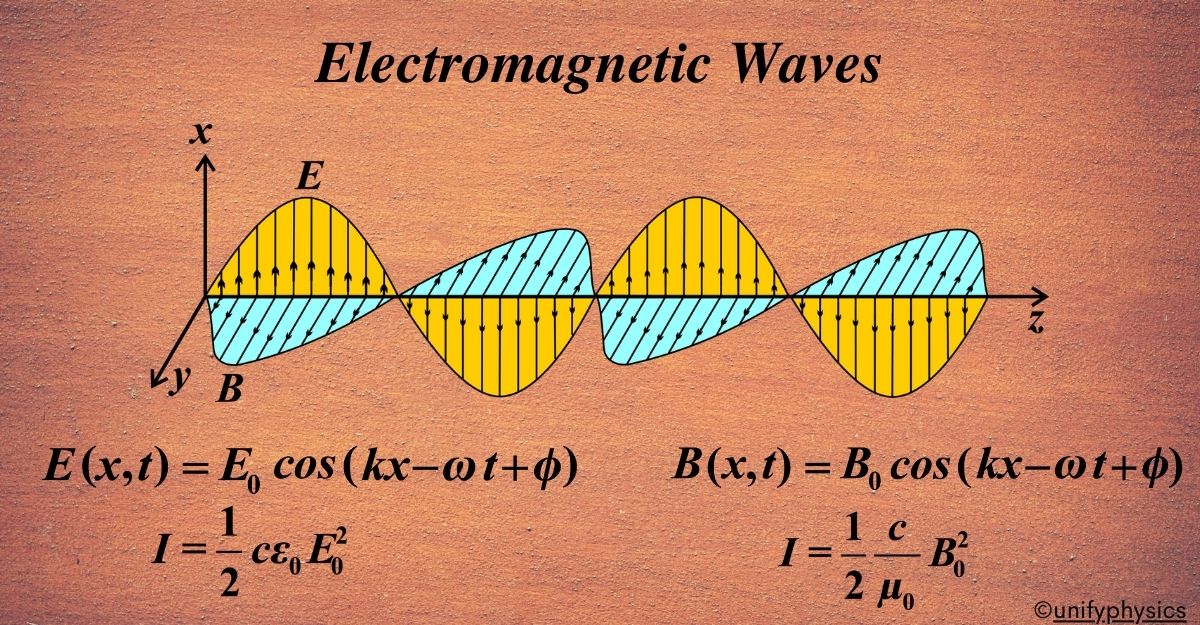
A simple way to represent an electromagnetic wave traveling in the x-direction is to use sine or cosine functions. Here’s what the equations look like:

\(\displaystyle E(x, t) = E_0 \cos(kx – \omega t + \phi) \)
\(\displaystyle B(x, t) = B_0 \cos(kx – \omega t + \phi) \)

• E(x, t) and B(x, t) are the electric and magnetic fields at position (x) and time (t).
• (E₀) and (B₀) are the maximum strengths of the electric and magnetic fields.
• (k) is the wave number, which tells us how many waves there are in a certain distance.
• (ω is the angular frequency, which tells us how many waves pass by in a certain time.
• (Φ) is the phase constant, which tells us where the wave starts.

The electric and magnetic fields in an electromagnetic wave are related to each other. The strength of the magnetic field (B₀) is directly proportional to the strength of the electric field (E₀) and inversely proportional to the speed of light (c):

\(\displaystyle B_0 = \frac{E_0}{c} \)

The speed of light (c) is a fundamental constant in physics, and it’s the speed at which all electromagnetic waves travel in a vacuum:

\(\displaystyle c = 3 \times 10^8 \, \text{m/s} \)

The wavelength (λ) is the distance between two consecutive peaks of the wave, and the frequency (f) is how many peaks pass a point every second. They are related to the wave number and angular frequency like this:

\(\displaystyle \lambda = \frac{2\pi}{k} \)
\(\displaystyle f = \frac{\omega}{2\pi} \)

They are also related to the speed of light:

\(\displaystyle c = \lambda f \)

When we put all these pieces together, we get a full picture of an electromagnetic wave. We can tell how it moves, how it changes over time, and how the electric and magnetic fields interact with each other.

Also Read: Displacement Current

Graphical Representation of Electromagnetic Waves

Graphically, these waves can be represented as sinusoidal waves, with the electric field and magnetic field oscillating perpendicular to each other. When we want to visualize electromagnetic waves, we often use a graph. This graph helps us see what the wave looks like as it travels through space. The most common way to represent an electromagnetic wave is by using a sinusoidal graph. This type of graph shows how the wave oscillates in a smooth, wave-like pattern over time.

On this graph, we can draw two waves:

• One wave represents the electric field (E), which might be shown as oscillating up and down.
• The other wave represents the magnetic field (B), which oscillates side to side, perpendicular to the electric field.

These two fields are always at right angles to each other, and they’re also perpendicular to the direction the wave is traveling. This is why electromagnetic waves are called transverse waves.

The highest points on the wave are called crests, and the lowest points are called troughs. The distance from one crest to the next, or from one trough to the next, is the wavelength of the wave. The direction that the wave is moving is usually shown with an arrow. This arrow is perpendicular to both the electric and magnetic fields, indicating the path that the wave is taking through space.

In a vacuum, all electromagnetic waves travel at the same speed—the speed of light, which is about 3 x 10^8 meters per second. This speed is constant and doesn’t change, no matter the frequency or wavelength of the wave.

By looking at the graphical representation, we can tell a lot about the wave:

• The amplitude of the waves tells us how strong the electric and magnetic fields are.
• The wavelength tells us how far apart the wave’s peaks are.
• The frequency tells us how many peaks pass a certain point every second.

Properties of Electromagnetic Waves

• Transverse Nature: Electromagnetic waves are transverse waves. This means that the oscillations of the electric and magnetic fields are perpendicular to the direction the wave is traveling.
• Oscillating Fields: The waves consist of two components: an electric field and a magnetic field. These fields oscillate at right angles to each other and to the direction of wave propagation.
• Speed in Vacuum: In a vacuum, electromagnetic waves travel at a constant velocity, which is the speed of light, approximately 3 x 10^8 m/s.
• No Medium Required: Unlike sound waves, electromagnetic waves do not require a material medium for propagation. They can travel through the vacuum of space.
• Wave Equation: Electromagnetic waves obey the wave equation ( c = f\lambda ), where ( c ) is the speed of light, ( f ) is the frequency, and ( \lambda ) is the wavelength. This equation shows that the product of the wavelength and frequency of an electromagnetic wave is a constant ( c ), which is the speed of light.
• In-Phase Oscillation: The electric and magnetic fields in an electromagnetic wave are in the same phase. This means that they reach their maximum and minimum values simultaneously.
• Amplitude Ratio: The ratio of the amplitudes of the electric field to the magnetic field is equal to the velocity of the wave. This relationship is crucial for understanding the energy carried by the wave.
• Spectrum Range: Electromagnetic waves cover a broad spectrum, from long-wavelength radio waves to short-wavelength gamma rays. Each part of the spectrum has different properties and uses.
• Energy Transfer: These waves transfer energy from one place to another. For example, sunlight carries energy from the Sun to Earth, which is essential for life.
• Polarization: Electromagnetic waves can be polarized. Polarization is the process by which the oscillations of the waves are aligned in a particular direction.
• Reflection and Refraction: Like other waves, electromagnetic waves can be reflected and refracted. This behavior is the basis for many optical technologies and instruments.
• Interference and Diffraction: Electromagnetic waves can interfere with each other, leading to patterns of constructive and destructive interference. They can also diffract around obstacles, spreading out as they pass through narrow openings.

Electromagnetic Wave Equation

The electromagnetic wave equation is a way to describe how electric and magnetic fields spread out as waves in space. It’s like a recipe that tells us how these fields behave and move.

Imagine you have a pond, and you drop a stone into it. You see ripples moving away from where the stone fell. Now, instead of water, imagine those ripples are made of electric and magnetic fields, and they’re moving through the air or even through the vacuum of space. That’s what the electromagnetic wave equation helps us understand.

The equation looks a bit complicated, but it’s really just a fancy way of saying that the electric field (E) and the magnetic field (B) create each other and move together as a wave. Here’s what the equation looks like:

\(\displaystyle \nabla^2 \vec{E} = \frac{1}{c^2} \frac{\partial^2 \vec{E}}{\partial t^2} \)
\(\displaystyle \nabla^2 \vec{B} = \frac{1}{c^2} \frac{\partial^2 \vec{B}}{\partial t^2} \)

• \(\displaystyle\nabla^2\) is a symbol that means we’re looking at how the fields change in space.
• \(\displaystyle\vec{E} \) and \(\displaystyle \vec{B}\) are the electric and magnetic fields.
• (c) is the speed of light, which is about 3 x 10⁸ meters per second.
• \(\displaystyle\frac{\partial^2}{\partial t^2}\) means we’re looking at how the fields change over time.

This equation tells us that the electric and magnetic fields in an electromagnetic wave are always changing, but they do so in a very specific and orderly way. They spread out from the source (like the stone in the pond), and they move at the speed of light.

So, in simple terms, the electromagnetic wave equation describes how electric and magnetic fields travel through space and time as waves, moving at the speed of light, and it’s a key part of how we understand the universe around us.

Intensity of Electromagnetic Waves

The intensity of an electromagnetic wave is the power per unit area carried by the wave. It is proportional to the square of the amplitude of the electric field. When we talk about the intensity of electromagnetic waves, we’re really talking about how much energy they carry and how that energy is distributed.

Intensity is a measure of the power that an electromagnetic wave transfers per unit area. In simpler terms, it tells us how strong the wave is. Imagine standing outside on a sunny day. The warmth you feel is because of the intensity of the sunlight hitting your skin.

Mathematically, intensity (I) is defined as the power (P) delivered per unit area (A) perpendicular to the direction of wave propagation. The formula looks like this:

\(\displaystyle I = \frac{P}{A} \)

The intensity is also related to the energy flow in the wave. It’s like how much energy is flowing through a certain area (like a window) every second. The unit of intensity is watts per square meter (W/m²). It’s a way of saying how many joules of energy are passing through one square meter every second.

Factors Affecting Intensity: The intensity of an electromagnetic wave depends on two things:

• The amplitude of the wave: A higher amplitude means a stronger wave and more intensity.
• The distance from the source: Intensity decreases as you move away from the source of the wave.

Let’s go back to the sunlight example. The intensity of sunlight is higher when there are no clouds because the power reaching you isn’t blocked. But on a cloudy day, the clouds scatter and absorb some of the sunlight, so the intensity is lower. We have two formulas to express the intensity of an electromagnetic wave:

Based on the Magnetic Field: \(\displaystyle I = \frac{P}{A} = \frac{1}{2} \frac{c}{\mu_0} B_0^2 \).

Based on the Electric Field: \(\displaystyle I = \frac{P}{A} = \frac{1}{2} c \epsilon_0 E_0^2 \).

• (c): This is the speed of light, which is about (3 × 10⁸) meters per second. It’s a fundamental constant in physics.
• (µ₀): The permeability of free space is a measure of how much resistance is encountered when forming a magnetic field in a classical vacuum.
• (B₀): The peak magnetic field strength is the maximum value the magnetic field reaches as the wave oscillates.
• \(\displaystyle\epsilon_0 \): The permittivity of free space is a measure of how an electric field affects and is affected by a vacuum.
• (E₀): The peak electric field strength is the maximum value the electric field reaches as the wave oscillates.

These formulas show that the intensity of an electromagnetic wave is directly proportional to the square of the peak values of the electric or magnetic fields. This means that if you double the strength of the electric or magnetic field, the intensity of the wave will increase by a factor of four.

The intensity is important because it’s related to the energy the wave can transfer. For example, the intensity of sunlight determines how much solar energy a panel can convert into electricity.

Speed of Electromagnetic Waves

When we talk about the speed of electromagnetic waves, we’re referring to how fast these waves travel through space. It’s a fundamental property that has some pretty amazing implications. The speed of electromagnetic waves in a vacuum is about 3 x 10⁸ meters per second. This is the speed of light, and it’s the fastest speed at which any information or energy can travel in the universe.

Let’s delve into the concept of the speed of electromagnetic waves and understand it through its fundamental formula, tailored for 12th-grade physics students: The speed of electromagnetic waves is a crucial concept in physics, representing how fast these waves travel through space. The speed (c) of electromagnetic waves in a vacuum is given by the formula:

\(\displaystyle c = \frac{1}{\sqrt{\mu_0 \epsilon_0}} \)

• (µ₀) is the permeability of free space, which is \(\displaystyle 4\pi \times 10^{-7} \) henry per meter (H/m).
• \(\displaystyle\epsilon_0 \) is the permittivity of free space, about ( 8.854 \times 10^{-12} ) farad per meter (F/m).
• Permeability (µ₀): This constant represents how much resistance is encountered when forming a magnetic field in a vacuum.
• Permittivity (\(\displaystyle\epsilon_0\)): This constant indicates how an electric field affects and is affected by a vacuum.

The speed of electromagnetic waves is significant because it’s not just the speed of light; it’s also the speed at which all electromagnetic waves travel, including radio waves, microwaves, infrared, visible light, ultraviolet, X-rays, and gamma rays.

While (c) is the speed in a vacuum, electromagnetic waves slow down when they travel through different media like air, water, or glass. The speed in a medium (v ) is related to the refractive index (n) of the medium:

\(\displaystyle v = \frac{c}{n} \)

The refractive index is a dimensionless number that describes how light propagates through that medium compared to a vacuum.

No matter what type of electromagnetic wave you’re dealing with—whether it’s radio waves, microwaves, visible light, or gamma rays—they all travel at the same speed in a vacuum. This uniform speed is one of the cornerstones of our understanding of physics. While the speed of light in a vacuum is constant, electromagnetic waves do slow down when they pass through different materials, like air, water, or glass. The speed in a medium depends on the medium’s electric and magnetic properties.

The speed of electromagnetic waves is crucial for everything from understanding how the universe works to practical applications like GPS and telecommunications. It’s also essential for the theory of relativity, which helps us understand how gravity and motion affect time and space. The speed of light is not just a number; it’s a fundamental part of the structure of the universe. It’s used to define distances in space and has been a key factor in many scientific discoveries.

So, in simple terms, the speed of electromagnetic waves is the speed at which light travels. It’s incredibly fast, always the same in a vacuum, and it’s a key part of how we understand the world around us.

Maxwell’s Wave Equation for Electromagnetic Waves

In a vacuum, Maxwell’s equations can be combined to produce the wave equation for electromagnetic waves. In matter, these equations are modified to account for the material’s properties.

Name	Equation in Vacuum	Equation in Matter
Modified Ampere-Maxwell Law	\(\displaystyle \nabla \times \vec{B} = \mu_0 \left( \vec{J} + \epsilon_0 \frac{\partial \vec{E}}{\partial t} \right) \)	\(\displaystyle \nabla \times \vec{B} = \mu \left( \vec{J} + \vec{J}_d + \vec{J}_s \right) = \mu \vec{J} + \mu_0 \epsilon_0 \frac{\partial \vec{E}}{\partial t} + \frac{\partial \vec{D}}{\partial t} \)
Faraday’s Law	\(\displaystyle \nabla \times \vec{E} = -\frac{\partial \vec{B}}{\partial t} \)	Same as in vacuum
Gauss’ Law	\(\displaystyle \nabla \cdot \vec{E} = \frac{\rho}{\epsilon_0} \)	\(\displaystyle \nabla \cdot \vec{D} = \rho_f \)
Gauss’ Law of Magnetism	\(\displaystyle \nabla \cdot \vec{B} = 0 \)	Same as in vacuum

Key Points to Understand:

• Modified Ampere-Maxwell Law: This equation shows how a changing electric field can create a magnetic field (and vice versa), which is the basis for electromagnetic waves.
• Faraday’s Law: Indicates that a changing magnetic field will induce a changing electric field, another fundamental concept for electromagnetic waves.
• Gauss’ Law: Relates the electric field to the charge distribution in space.
• Gauss’ Law of Magnetism: States that there are no ‘magnetic charges’ analogous to electric charges, and magnetic field lines are always closed loops.

In a vacuum, these equations are simpler because there are no materials to affect the fields. In matter, the equations account for how the material interacts with the fields, which can change how the waves behave.

Integral Form of the Maxwell Equation for a Vacuum

The integral form of Maxwell’s equations describes how electric and magnetic fields relate to the electric charge and current that produce them.

Name	Integral Form in Vacuum	Explanation
Modified Ampere-Maxwell Law	\(\displaystyle \oint \vec{B} \cdot d\vec{s} = \mu_0 I + \mu_0 \epsilon_0 \frac{d}{dt}\int \vec{E} \cdot d\vec{a} \)	This law combines Ampere’s Law with Maxwell’s addition. It states that the magnetic field \(\displaystyle \vec{B} \) around a closed loop is caused by the electric current (I) and the change in electric flux through the surface enclosed by the loop.
Faraday’s Law	\(\displaystyle \oint \vec{E} \cdot d\vec{l} = -\frac{d}{dt}\int \vec{B} \cdot d\vec{a} \)	Faraday’s Law of induction tells us that a changing magnetic field through a loop induces an electric field around the loop. The negative sign indicates that the induced electric field opposes the change in magnetic flux.
Gauss’ Law	\(\displaystyle \oint \vec{E} \cdot d\vec{a} = \frac{q}{\epsilon_0} \)	Gauss’ Law relates the electric flux through a closed surface to the charge ( q ) enclosed by that surface. It tells us that electric charges produce an electric field.
Gauss’ Law for Magnetism	\(\displaystyle \oint \vec{B} \cdot d\vec{a} = 0 \)	This law states that the magnetic flux through a closed surface is zero, which implies that there are no isolated magnetic charges (or ‘magnetic monopoles’).

These integral forms are used to calculate the effects of electric and magnetic fields over a surface or loop, which is essential for understanding how electromagnetic fields behave in a vacuum.

Limitations of Maxwell’s Wave Equation

Maxwell’s equations were groundbreaking in their ability to describe how electric and magnetic fields propagate as waves. However, they do have some limitations:

• Classical Nature: Maxwell’s equations are based on classical physics. They work well for large-scale phenomena but cannot explain atomic and subatomic processes where quantum mechanics is needed.
• Black Body Radiation: The equations couldn’t explain the observed spectrum of black body radiation, which led to the development of quantum theory.
• Photoelectric Effect: They fail to account for the photoelectric effect, where light can eject electrons from a material. This effect was explained by Einstein’s quantum theory of light.
• Heat Capacity of Solids: Maxwell’s equations do not explain the variation in heat capacity of solids as a function of temperature, which was later explained by quantum mechanics.
• Line Spectra of Atoms: The equations do not account for the line spectra of atoms, especially hydrogen, which are explained by the quantized energy levels in atoms.

Maxwell’s equations brilliantly describe the classical behavior of electromagnetic fields and waves, they do not address the quantum effects that become significant at very small scales or with high-frequency electromagnetic radiation. These limitations paved the way for the development of quantum mechanics, which provides a more complete understanding of the behavior of light and matter at the atomic level.

Applications of Electromagnetic Waves

Electromagnetic waves are utilized in various technologies and everyday applications. Here are some key applications explained in a way that’s easy to understand:

1. Radio Waves

• Communication: Radio waves are extensively used in communication systems, including AM and FM radio, television broadcasts, and mobile phone signals. These waves can travel long distances and penetrate through buildings, making them ideal for transmitting information.
• Navigation: GPS (Global Positioning System) uses radio waves to determine the exact location of a receiver on Earth. Satellites send signals to the GPS receivers, which calculate their position based on the time it takes for the signals to arrive.

2. Microwaves

• Cooking: Microwaves are used in microwave ovens to cook food. The microwaves cause water molecules in the food to vibrate, producing heat that cooks the food.
• Communication: Microwaves are also used in certain communication technologies, such as satellite communication and WiFi. They can carry large amounts of data over long distances with minimal interference.

3. Infrared (IR) Waves

• Remote Controls: Infrared waves are used in remote controls for TVs, air conditioners, and other electronic devices. The remote sends an infrared signal to the device, which interprets the signal and performs the corresponding action.
• Thermal Imaging: Infrared cameras can detect heat emitted by objects. This technology is used in night vision equipment, medical imaging to detect heat patterns in the body, and in building inspections to find heat leaks.

4. Visible Light

• Vision: Visible light is the range of electromagnetic waves that the human eye can see. It allows us to perceive colors and shapes, enabling us to navigate and understand our environment.
• Lighting: Visible light is used in various lighting applications, including household lighting, street lamps, and vehicle headlights. Different types of bulbs, such as LEDs and incandescent bulbs, emit visible light to illuminate spaces.

5. Ultraviolet (UV) Light

• Sterilization: UV light has the ability to kill bacteria and viruses, making it useful for sterilizing medical equipment, water, and air.
• Tanning: Exposure to UV light causes the skin to tan. Tanning beds use UV lamps to simulate sunlight and tan the skin.
• Security: UV light is used in security features of banknotes and identification cards. Special inks that fluoresce under UV light help to prevent counterfeiting.

6. X-Rays

• Medical Imaging: X-rays can penetrate the body and are used to create images of bones and other internal structures. This is essential for diagnosing fractures, infections, and diseases.
• Airport Security: X-ray machines are used in airport security to scan luggage and ensure that no dangerous items are being carried on board.

7. Gamma Rays

• Cancer Treatment: Gamma rays are used in radiation therapy to treat cancer. The high-energy waves can destroy cancer cells, helping to shrink tumors and eliminate the disease.
• Medical Imaging: Gamma rays are also used in certain imaging techniques, such as PET (Positron Emission Tomography) scans, to diagnose and monitor medical conditions.
• Sterilization: Like UV light, gamma rays can sterilize medical equipment by killing bacteria and viruses, ensuring that tools are safe for use in surgeries and other procedures.

These applications show how electromagnetic waves are integral to many aspects of modern life, from healthcare to communication and beyond. Understanding these applications helps students appreciate the practical importance of the physics concepts they learn in class.

Solved Examples

Example 1: Calculate the speed of an electromagnetic wave in a vacuum if the permeability of free space (µ₀) is \(\displaystyle 4\pi \times 10^{-7} \, \text{H/m}\) and the permittivity of free space (\(\displaystyle\epsilon_0\)) is \(\displaystyle 8.854 \times 10^{-12} \, \text{F/m}\).

Solution: The speed of electromagnetic waves in a vacuum (c) is given by:

\(\displaystyle c = \frac{1}{\sqrt{\mu_0 \epsilon_0}} \)

Substituting the given values:

\(\displaystyle c = \frac{1}{\sqrt{(4\pi \times 10^{-7}) \times (8.854 \times 10^{-12})}} \)

\(\displaystyle c = \frac{1}{\sqrt{35.416 \times 10^{-19}}} \)

\(\displaystyle c = \frac{1}{5.95 \times 10^{-10}} \)

\(\displaystyle c \approx 3 \times 10^8 \, \text{m/s} \)

Therefore, the speed of electromagnetic waves in a vacuum is \(\displaystyle 3 \times 10^8 \, \text{m/s}\).

Example 2: An electromagnetic wave has an electric field amplitude of \(\displaystyle E_0 = 100 \, \text{V/m}\). Calculate the intensity of the electromagnetic wave.

Solution: The intensity (I) of an electromagnetic wave is given by:

\(\displaystyle I = \frac{1}{2} \epsilon_0 c E_0^2 \)

• \(\displaystyle\epsilon_0 = 8.854 \times 10^{-12} \, \text{F/m}\)
• \(\displaystyle c = 3 \times 10^8 \, \text{m/s}\)
• \(\displaystyle E_0 = 100 \, \text{V/m}\)

Substituting the values:

\(\displaystyle I = \frac{1}{2} \times 8.854 \times 10^{-12} \times 3 \times 10^8 \times (100)^2 \)

\(\displaystyle I = \frac{1}{2} \times 8.854 \times 10^{-12} \times 3 \times 10^8 \times 10^4 \)

\(\displaystyle I = \frac{1}{2} \times 8.854 \times 10^{-12} \times 3 \times 10^{12} \)

\(\displaystyle I = \frac{1}{2} \times 26.562 \)

\(\displaystyle I = 13.281 \, \text{W/m}^2 \)

Therefore, the intensity of the electromagnetic wave is \(\displaystyle 13.281 \, \text{W/m}^2\).

Example 3: Show that the wave equation \(\displaystyle\frac{\partial^2 E}{\partial x^2} = \mu_0 \epsilon_0 \frac{\partial^2 E}{\partial t^2}\) is satisfied by an electromagnetic wave with electric field \(\displaystyle E = E_0 \sin(kx – \omega t)\).

Solution: Given,

\(\displaystyle E = E_0 \sin(kx – \omega t) \)

First, calculate the second spatial derivative:

\(\displaystyle \frac{\partial E}{\partial x} = E_0 k \cos(kx – \omega t) \)

\(\displaystyle \frac{\partial^2 E}{\partial x^2} = -E_0 k^2 \sin(kx – \omega t) \)

Now, calculate the second time derivative:

\(\displaystyle \frac{\partial E}{\partial t} = -E_0 \omega \cos(kx – \omega t) \)

\(\displaystyle \frac{\partial^2 E}{\partial t^2} = -E_0 \omega^2 \sin(kx – \omega t) \)

Substitute these into the wave equation:

\(\displaystyle \frac{\partial^2 E}{\partial x^2} = \mu_0 \epsilon_0 \frac{\partial^2 E}{\partial t^2} \)

\(\displaystyle -E_0 k^2 \sin(kx – \omega t) = \mu_0 \epsilon_0 (-E_0 \omega^2 \sin(kx – \omega t)) \)

\(\displaystyle k^2 = \mu_0 \epsilon_0 \omega^2 \)

Since \(\displaystyle\omega = kc\) and \(\displaystyle c = \frac{1}{\sqrt{\mu_0 \epsilon_0}}\):

\(\displaystyle k^2 = \mu_0 \epsilon_0 k^2 c^2 \)

\(\displaystyle 1 = \mu_0 \epsilon_0 c^2 \)

\(\displaystyle 1 = \mu_0 \epsilon_0 \left(\frac{1}{\mu_0 \epsilon_0}\right) \)

1 = 1

Hence, the wave equation is satisfied by the given electric field.

Example 4: Verify the integral form of Gauss’s law for electricity \(\displaystyle\oint_S \mathbf{E} \cdot d\mathbf{A} = \frac{Q_{\text{enc}}}{\epsilon_0}\) for a point charge (Q) in vacuum.

Solution: Consider a point charge (Q) at the origin. The electric field at a distance (r) from the charge is given by:

\(\displaystyle \mathbf{E} = \frac{Q}{4\pi \epsilon_0 r^2} \hat{r} \)

To verify Gauss’s law, consider a spherical surface of radius (r) centered on the charge. The surface integral of \(\displaystyle\mathbf{E}\) over the sphere is:

\(\displaystyle\oint_S \mathbf{E} \cdot d\mathbf{A} = \oint_S \frac{Q}{4\pi \epsilon_0 r^2} \hat{r} \cdot d\mathbf{A} \)

Since \(\displaystyle\mathbf{E} \) and \(\displaystyle d\mathbf{A} \) are in the same direction (\(\displaystyle\hat{r}\)):

\(\displaystyle \oint_S \mathbf{E} \cdot d\mathbf{A} = \frac{Q}{4\pi \epsilon_0 r^2} \oint_S dA \)

The area of the spherical surface is \(\displaystyle 4\pi r^2\):

\(\displaystyle \oint_S dA = 4\pi r^2 \)

Therefore:

\(\displaystyle \oint_S \mathbf{E} \cdot d\mathbf{A} = \frac{Q}{4\pi \epsilon_0 r^2} \cdot 4\pi r^2 \)

\(\displaystyle\oint_S \mathbf{E} \cdot d\mathbf{A} = \frac{Q}{\epsilon_0} \)

This confirms Gauss’s law in integral form for a point charge in a vacuum.

Example 5: Calculate the energy density of an electromagnetic wave with electric field amplitude \(\displaystyle E_0 = 200 \, \text{V/m}\).

Solution: The energy density (u) of an electromagnetic wave is given by:

\(\displaystyle u = \frac{1}{2} \epsilon_0 E_0^2 \)

• \(\displaystyle\epsilon_0 = 8.854 \times 10^{-12} \, \text{F/m}\)
• \(\displaystyle E_0 = 200 \, \text{V/m}\)

Substituting the values:

\(\displaystyle u = \frac{1}{2} \times 8.854 \times 10^{-12} \times (200)^2 \)

\(\displaystyle u = \frac{1}{2} \times 8.854 \times 10^{-12} \times 40000 \)

\(\displaystyle u = \frac{1}{2} \times 3.5416 \times 10^{-7} \)

\(\displaystyle u = 1.7708 \times 10^{-7} \, \text{J/m}^3 \)

Therefore, the energy density of the electromagnetic wave is \(\displaystyle 1.7708 \times 10^{-7} \, \text{J/m}^3\).

FAQs