Energy Stored In Capacitors

The story of capacitors begins in the mid-18th century. Two European scientists, Ewald Georg von Kleist, and Pieter van Musschenbroek, independently discovered that electric charge could be stored. This was the birth of the Leyden jar, the earliest form of the capacitor². Imagine a glass jar filled with water, with a metal wire passing through the cork top, dipping into the water. The jar would be charged with static electricity, and this charge could be stored and later released. This was a groundbreaking discovery at the time!

The Leyden jar was just the beginning. Over time, the design of capacitors evolved. The term ‘condenser’ was initially used, which you might still hear in some contexts, like in ‘condenser microphones’. The basic principle remained the same: two conductors separated by an insulator (or dielectric), storing energy in the electric field created between them.

Fast forward to the 20th century, capacitors found a new role in the burgeoning field of electronics. They were used in radio tuning circuits and as part of the power supply systems in electronic devices. Perhaps most notably, the property of energy storage in capacitors was exploited as dynamic memory in early digital computers.

In the early 1950s, General Electric engineers experimented with porous carbon electrodes, leading to the development of supercapacitors. These are capacitors with very high capacitance values, capable of storing tremendous amounts of energy compared to traditional capacitors.

Today, capacitors are ubiquitous in electronic circuits. They block direct current while allowing alternating current to pass, smooth out power supply outputs, and are essential in timing and memory devices.

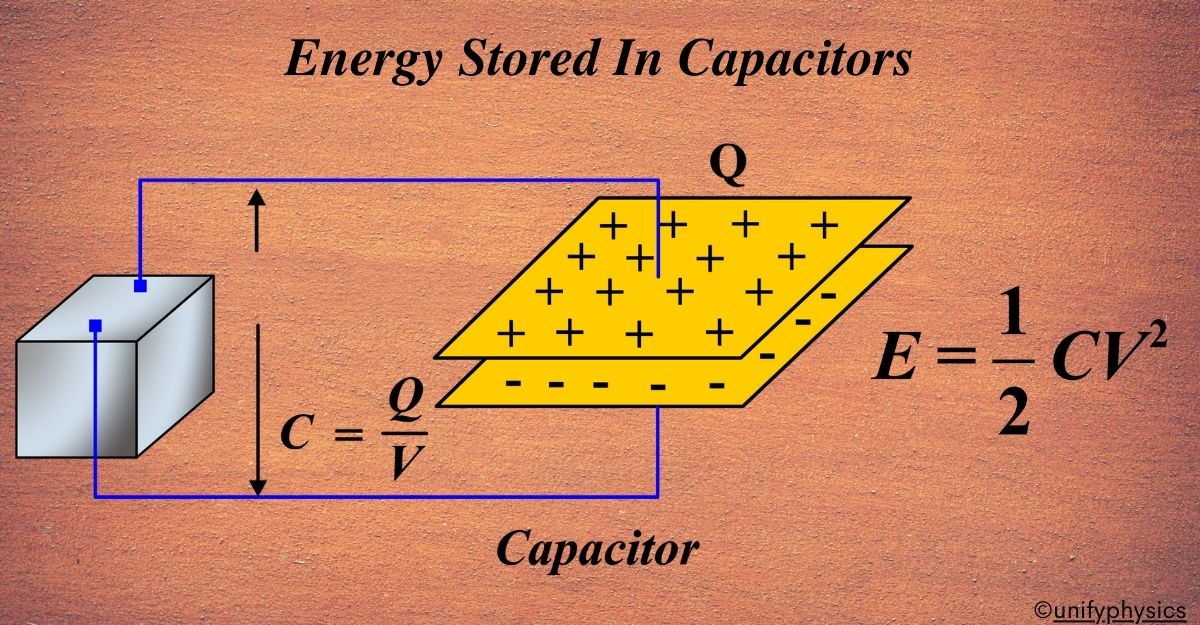
Energy Stored in a Capacitor

A capacitor stores energy in the form of an electric field created between two conductors on which equal but opposite electric charges have been placed. Think of a capacitor as a little energy bank. It’s a device that can store and release electrical energy. It has two plates separated by an insulator (dielectric).

When a voltage is applied across the plates, one plate becomes positively charged, while the other becomes negatively charged. This creates an electric field between the plates, and it’s within this field that energy is stored.

The energy (E) stored in a capacitor is given by the formula:

\(\displaystyle E = \frac{1}{2}CV^2 \)

where (C) is the capacitance (the capacitor’s ability to store charge), and (V) is the voltage across the capacitor.

Imagine slowly transferring charge from one plate to the other. As you move each tiny bit of charge, you’re doing work against the electric field. This work gets stored as potential energy. By the time you’ve moved enough charge to reach the voltage (V), you’ve stored a certain amount of energy, which we calculate with the formula above.

The ability to store energy in an electric field is crucial. It allows capacitors to release energy quickly, which is essential in many electronic devices, from cameras (flash) to computers (memory and power smoothing).

Capacitors are like sponges for electric charge. They soak up energy when connected to a power source and squeeze it out when needed. The energy stored in a capacitor is crucial for managing power in electronic circuits, making them an indispensable component of modern technology.

Energy Stored in a Capacitor Derivation

When we charge a capacitor, we’re essentially moving charges from one plate to another, against the electric field between the plates. This requires work, and this work is what gets stored as energy in the capacitor.

To move a small amount of charge (dq) from one plate to another, the work done (dW) is equal to the potential difference (V) times the small charge (dq):

\(\displaystyle dW = Vdq \)

The potential difference (V) across the capacitor can be expressed in terms of the charge (q) already on the capacitor and its capacitance (C):

\(\displaystyle V = \frac{q}{C} \)

Substituting this into our expression for work done, we get:

\(\displaystyle dW = \frac{q}{C}dq \)

To find the total work done to move charge from (q = 0) to (q = Q), we integrate:

\(\displaystyle W = \int_0^Q \frac{q}{C}dq \)

This integration gives us:

\(\displaystyle W = \frac{1}{2}\frac{Q^2}{C} \)

The work done on the charges becomes the energy (E) stored in the capacitor.

Since (Q = CV), we can substitute (Q) in the expression for (W) to get the energy stored in terms of capacitance and voltage:

\(\displaystyle E = \frac{1}{2}CV^2 \)

The final expression tells us that the energy stored in a capacitor is directly proportional to the square of the voltage across it and its capacitance. This means that if you double the voltage, the energy stored increases by a factor of four.

The energy stored in a capacitor is the work done to move charge against the electric field between the plates. It’s an example of potential energy, which in this case, is stored in the electric field itself.

Energy Density of a Charged Capacitor

Energy density is a measure of how much energy is stored in a given space. In the context of capacitors, it tells us how much energy is stored in the electric field between the capacitor’s plates per unit volume.

For a parallel-plate capacitor, the volume where the electric field exists is the area of one plate (A) multiplied by the distance between the plates (d). So, the volume is (Ad).

The total energy (U) stored in a capacitor is given by the formula:

\(\displaystyle U = \frac{1}{2}CV^2 \)

where (C) is the capacitance and (V) is the voltage across the plates.

Energy density is the amount of energy stored per unit volume. For a capacitor, this refers to the energy stored in the electric field between its plates. The energy density is the energy per unit volume, so we divide the total energy by the volume:

\(\displaystyle u = \frac{U}{V} \)

Substituting the expressions for (U) and (V) we get:

\(\displaystyle u = \frac{\frac{1}{2}CV^2}{Ad} \)

Simplifying the expression, we find the energy density of a charged capacitor:

\(\displaystyle u = \frac{1}{2}\frac{C}{A}\frac{V^2}{d} \)

Since ( \(\displaystyle\frac{C}{A}\) ) is the capacitance per unit area, and (\(\displaystyle \frac{V^2}{d} \)) represents the electric field strength squared (E²), we can also express the energy density in terms of the electric field:

\(\displaystyle u = \frac{1}{2}\epsilon_0 E^2 \)

Here, (\(\displaystyle \epsilon_0 \)) is the permittivity of free space, and (E) is the electric field strength.

The derived expression shows that the energy density inside a capacitor is proportional to the square of the electric field strength. This means that a stronger electric field will result in a higher energy density. The energy density of a charged capacitor tells us how efficiently the capacitor stores energy within its electric field.

Common Potential During System Of Charges

What is Common Potential? The concept of common potential is all about balance and equilibrium. It’s a fundamental principle that applies not just to capacitors, but to many areas of physics and engineering. It’s the electrical equivalent of leveling the playing field, ensuring that every component in a circuit is at the same potential, ready to work together harmoniously.

Imagine you have two water tanks at different heights connected by a pipe. Water will flow from the higher tank to the lower one until the water levels are the same in both tanks. Similarly, when two capacitors with different charges are connected, the charge flows until they reach a common potential.

Each capacitor has a certain capacity to hold charge, known as capacitance (C), and an initial potential (V), which is the voltage across its plates.

When you connect two capacitors, the charges redistribute. The capacitor with a higher initial potential will lose some charge, and the one with a lower potential will gain charge.

The charges move until both capacitors have the same potential. This final potential is the common potential.

The common potential (V_f) can be calculated using the formula:

\(\displaystyle V_f = \frac{C_1V_1 + C_2V_2}{C_1 + C_2} \)

Here, (C₁) and (C₂) are the capacitances, and (V₁) and (V₂) are the initial potentials of the two capacitors.

Understanding common potential is crucial because it helps us predict how a system will behave when different charged bodies interact. It’s like knowing how much water will flow between the tanks or how the charges will balance out in a circuit.

Derivation: When two capacitors with different initial potentials are connected, they share charges until they reach a common potential. This is similar to how water levels even out when two containers are connected.

Consider two capacitors, Capacitor 1 with capacitance (C₁) and initial potential (V₁), and Capacitor 2 with capacitance (C₂) and initial potential (V₂).

When connected, charge will flow until both capacitors have the same potential, (V_f). The final charges on Capacitor 1 and Capacitor 2 will be (C₁V_f ) and (C₂V_f ), respectively.

The total charge before connection is the sum of the initial charges on both capacitors:

\(\displaystyle Q_{total} = C_1V_1 + C_2V_2 \)

After connection, the total charge remains the same but is redistributed between the two capacitors:

\(\displaystyle Q_{total} = C_1V_f + C_2V_f \)

To find the common potential, we equate the total charge before and after the connection:

\(\displaystyle C_1V_1 + C_2V_2 = C_1V_f + C_2V_f \)

Factoring out (V_f), we get:

\(\displaystyle V_f = \frac{C_1V_1 + C_2V_2}{C_1 + C_2} \)

The derived expression shows that the common potential is a weighted average of the initial potentials, weighted by the capacitances of the capacitors. This means that the capacitor with the larger capacitance will have a greater influence on the final common potential.

The concept of common potential during a system of charges is an application of the conservation of charge. It’s important in circuits where capacitors are used, as it determines how the system will behave when different capacitors interact.

Loss Of Energy During Sharing Of Charges

The loss of energy during the sharing of charges is like the loss of kinetic energy when sliding to a stop. It’s a natural consequence of the laws of physics that govern energy transformation and conservation.

Imagine two friends with different amounts of money who decide to pool their money together and then share it equally. After sharing, they might have more money together, but individually, they might end up with less than they started with. Similarly, when two capacitors with different charges come together, they share their charges to reach a common potential, and during this process, some energy is lost.

Each capacitor has some initial energy based on its charge and voltage. When connected, the capacitors share their charges. The one with higher voltage loses charge, and the one with lower voltage gains charge. They eventually reach a common potential, where the system’s total energy is less than the sum of their initial energies.

The loss of energy (\(\displaystyle\Delta E \)) can be derived by subtracting the final energy of the system from the initial energy of the individual capacitors.

The formula for the loss of energy is:

\(\displaystyle \Delta E = \frac{1}{2}C_1V_1^2 + \frac{1}{2}C_2V_2^2 – \frac{1}{2}(C_1 + C_2)V_f^2 \)

Here, (C₁) and (C₂) are the capacitances, (V₁) and (V₂) are the initial voltages, and (V_f) is the final common potential.

The energy isn’t just disappearing; it’s transforming, usually into heat due to the resistance in the circuit. This is similar to how kinetic energy is transformed into heat due to friction when an object slides to a stop.

Derivation: Imagine two capacitors, each initially charged to different potentials. When they are connected, charges will redistribute until both capacitors reach a common potential. During this process, some energy is lost. Let’s find out how much.

The initial energy stored in the first capacitor (E₁) is given by:

\(\displaystyle E_1 = \frac{1}{2}C_1V_1^2 \)

Similarly, the initial energy stored in the second capacitor (E₂) is:

\(\displaystyle E_2 = \frac{1}{2}C_2V_2^2 \)

Here, ( C₁ ) and ( C₂ ) are the capacitances, and ( V₁ ) and ( V₂ ) are the initial potentials of the first and second capacitors, respectively.

After connecting the capacitors, they will share charges and reach a common potential (V_f):

\(\displaystyle V_f = \frac{C_1V_1 + C_2V_2}{C_1 + C_2} \)

The final energy stored in both capacitors when they reach the common potential is:

\(\displaystyle E_{final} = \frac{1}{2}(C_1 + C_2)V_f^2 \)

The loss of energy (\(\displaystyle\Delta E \)) is the difference between the initial and final energies:

\(\displaystyle \Delta E = (E_1 + E_2) – E_{final} \)

Substituting the expressions for (E₁), (E₂), and (E_final), we get:

\(\displaystyle \Delta E = \frac{1}{2}C_1V_1^2 + \frac{1}{2}C_2V_2^2 – \frac{1}{2}(C_1 + C_2)V_f^2 \)

After simplifying, we find the expression for the loss of energy:

\(\displaystyle \Delta E = \frac{C_1C_2}{2(C_1 + C_2)}(V_1 – V_2)^2 \)

The derived expression shows that the loss of energy is proportional to the square of the difference in the initial potentials and inversely proportional to the sum of the capacitances. This means that if the initial potentials are very different or the capacitances are small, the loss of energy will be greater.

The loss of energy during the sharing of charges is an important concept to understand, as it has practical implications in circuits where capacitors are used. It’s a manifestation of the conservation of energy principle, showing that energy is not destroyed but transformed, in this case, likely into heat due to the resistance in the circuit.

Application of Energy Stored In Capacitors

Capacitors are used in various applications such as energy storage in power grids, smoothing out fluctuations in electronic circuits, timing devices, and even defibrillators to deliver quick bursts of energy.

Capacitors are like the unsung heroes of the electronic world. They store energy quietly but spring into action when needed. Here’s how they make a difference in various applications:

• Picture a medical drama where doctors shout, “Clear!” and use paddles on a patient’s chest. That’s a defibrillator, which uses the energy stored in capacitors to deliver a life-saving electric shock to the heart.
• Your calculator or smartphone might not seem like a hub of energy, but the capacitors inside them store energy to maintain memory and manage power efficiently.
• When you take a picture with a flash, a capacitor discharges a burst of energy to produce that bright light, capturing a moment in time.
• In audio equipment, capacitors store energy that’s released to smooth out the power supply, ensuring your music is free from distortion.
• Ever wonder how your computer stays on during a power cut? UPS systems use capacitors to provide a quick supply of energy, giving you time to save your work.
• Electric and hybrid cars use capacitors to store energy when braking. This energy is then used to help power the car, making it more efficient.
• In industries, capacitors store energy to start heavy-duty motors and stabilize voltage, keeping machinery running smoothly.
• When the power goes out, capacitors in computers release stored energy to save your data until the backup kicks in.

Capacitors are everywhere, storing energy and releasing it precisely when needed. They’re in your gadgets, cars, cameras, and even in life-saving medical equipment. Understanding their applications shows us just how vital these components are in our daily lives and the technology we depend on.

Also Read: Combination of Capacitors

Solved Example

Problem 1: A capacitor of capacitance (5 µF) is charged to a potential difference of (100 V). Calculate the energy stored in the capacitor.

Solution: The energy (U) stored in a capacitor is given by:

\(\displaystyle U = \frac{1}{2} C V^2 \)

Calculate (U):

\(\displaystyle U = \frac{1}{2} \times 5 \times 10^{-6} \times (100)^2 \)
\(\displaystyle U = \frac{1}{2} \times 5 \times 10^{-6} \times 10^4 \)
\(\displaystyle U = \frac{1}{2} \times 5 \times 10^{-2} \)
\(\displaystyle U = 0.25 \, \text{J} \)

Therefore, the energy stored in the capacitor is (0.25 J).

Problem 2:A parallel plate capacitor with a plate area of (0.1 m²) and a plate separation of (0.01 m) is charged to a potential difference of (200 V). Calculate the energy density between the plates of the capacitor.

Solution: The energy density (u) is given by:

\(\displaystyle u = \frac{U}{V} \)

First, calculate the capacitance (C):

\(\displaystyle C = \epsilon_0 \frac{A}{d} \)

where (\(\displaystyle \epsilon_0 = 8.854 \times 10^{-12} \, \text{F/m} \)).

\(\displaystyle C = 8.854 \times 10^{-12} \frac{0.1}{0.01} \)
\(\displaystyle C = 8.854 \times 10^{-12} \times 10 \)
\(\displaystyle C = 8.854 \times 10^{-11} \, \text{F} \)

Next, calculate the energy (U):

\(\displaystyle U = \frac{1}{2} C V^2 \)
\(\displaystyle U = \frac{1}{2} \times 8.854 \times 10^{-11} \times (200)^2 \)
\(\displaystyle U = \frac{1}{2} \times 8.854 \times 10^{-11} \times 40000 \)
\(\displaystyle U = 1.7708 \times 10^{-6} \, \text{J} \)

Now, calculate the volume (V):

\(\displaystyle V = A \times d \)
\(\displaystyle V = 0.1 \times 0.01 \)
\(\displaystyle V = 0.001 \, \text{m}^3 \)

Finally, calculate the energy density (u):

\(\displaystyle u = \frac{1.7708 \times 10^{-6}}{0.001} \)
\(\displaystyle u = 1.7708 \times 10^{-3} \, \text{J/m}^3 \)

Therefore, the energy density between the plates of the capacitor is (\(\displaystyle 1.7708 \times 10^{-3} \, \text{J/m}^3 \)).

Problem 3: Two capacitors, (C₁ = 3 µF) charged to (V₁ = 100 V) and ( C₂ = 6 µF) charged to ( V₂ = 0 V), are connected in parallel. Calculate the common potential after they are connected.

Solution: The charge on (C₁) before connection, (Q₁):

\(\displaystyle Q_1 = C_1 V_1 \)
\(\displaystyle Q_1 = 3 \times 10^{-6} \times 100 \)
\(\displaystyle Q_1 = 3 \times 10^{-4} \, \text{C} \)

The charge on (C₂) before connection, (Q₂):

\(\displaystyle Q_2 = C_2 V_2 \)
\(\displaystyle Q_2 = 6 \times 10^{-6} \times 0 \)
\(\displaystyle Q_2 = 0 \, \text{C} \)

The total charge (Q_total) is conserved:

\(\displaystyle Q_{total} = Q_1 + Q_2 \)
\(\displaystyle Q_{total} = 3 \times 10^{-4} + 0 \)
\(\displaystyle Q_{total} = 3 \times 10^{-4} \, \text{C} \)

The equivalent capacitance (C_eq) of the parallel combination:

\(\displaystyle C_{eq} = C_1 + C_2 \)
\(\displaystyle C_{eq} = 3 \times 10^{-6} + 6 \times 10^{-6} \)
\(\displaystyle C_{eq} = 9 \times 10^{-6} \, \text{F} \)

The common potential (V) is given by:

\(\displaystyle V = \frac{Q_{total}}{C_{eq}} \)
\(\displaystyle V = \frac{3 \times 10^{-4}}{9 \times 10^{-6}} \)
\(\displaystyle V = \frac{3}{9} \times 10^2 \)
\(\displaystyle V = \frac{1}{3} \times 10^2 \)
\(\displaystyle V = 33.33 \, \text{V} \)

Therefore, the common potential after the capacitors are connected is ( 33.33 V).

Problem 4: Two capacitors, (C₁ = 2 µF) charged to (V₁ = 150 V) and (C₂ = 4 µF) charged to (V₂ = 0 V), are connected in parallel. Calculate the loss of energy during the sharing of charges.

Solution: First, calculate the initial energy stored in the capacitors.

Initial energy in (C₁):

\(\displaystyle U_1 = \frac{1}{2} C_1 V_1^2 \)
\(\displaystyle U_1 = \frac{1}{2} \times 2 \times 10^{-6} \times (150)^2 \)
\(\displaystyle U_1 = \frac{1}{2} \times 2 \times 10^{-6} \times 22500 \)
\(\displaystyle U_1 = 22.5 \times 10^{-3} \, \text{J} \)
\(\displaystyle U_1 = 22.5 \, \text{mJ} \)

Initial energy in (C₂):

\(\displaystyle U_2 = \frac{1}{2} C_2 V_2^2 \)
\(\displaystyle U_2 = \frac{1}{2} \times 4 \times 10^{-6} \times 0 \)
\(\displaystyle U_2 = 0 \, \text{J} \)

Total initial energy:

\(\displaystyle U_{initial} = U_1 + U_2 \)
\(\displaystyle U_{initial} = 22.5 \, \text{mJ} \)

Next, calculate the common potential (V) after connection:

\(\displaystyle C_{eq} = C_1 + C_2 \)
\(\displaystyle C_{eq} = 2 \times 10^{-6} + 4 \times 10^{-6} \)
\(\displaystyle C_{eq} = 6 \times 10^{-6} \, \text{F} \)

Total charge (Q_total):

\(\displaystyle Q_{total} = C_1 V_1 \)
\(\displaystyle Q_{total} = 2 \times 10^{-6} \times 150 \)
\(\displaystyle Q_{total} = 3 \times 10^{-4} \, \text{C} \)

Common potential (V):

\(\displaystyle V = \frac{Q_{total}}{C_{eq}} \)
\(\displaystyle V = \frac{3 \times 10^{-4}}{6 \times 10^{-6}} \)
\(\displaystyle V = 50 \, \text{V} \)

Energy stored after connection:

\(\displaystyle U_{final} = \frac{1}{2} C_{eq} V^2 \)
\(\displaystyle U_{final} = \frac{1}{2} \times 6 \times 10^{-6} \times (50)^2 \)
\(\displaystyle U_{final} = \frac{1}{2} \times 6 \times 10^{-6} \times 2500 \)
\(\displaystyle U_{final} = 7.5 \times 10^{-3} \, \text{J} \)
\(\displaystyle U_{final} = 7.5 \, \text{mJ} \)

Loss of energy:

\(\displaystyle \Delta U = U_{initial} – U_{final} \)
\(\displaystyle \Delta U = 22.5 \, \text{mJ} – 7.5 \, \text{mJ} \)
\(\displaystyle \Delta U = 15 \, \text{mJ} \)

Therefore, the loss of energy during the sharing of charges is (15 mJ).

Problem 5: Calculate the energy stored in a spherical capacitor with inner radius (r₁ = 2 cm) and outer radius (r₂ = 4 cm), charged to a potential difference of ( V = 100 V).

Solution: The capacitance (C) of a spherical capacitor is given by:

\(\displaystyle C = 4 \pi \epsilon_0 \frac{r_1 r_2}{r_2 – r_1} \)

Calculate (C):

\(\displaystyle C = 4 \pi \times 8.854 \times 10^{-12} \frac{2 \times 10^{-2} \times 4 \times 10^{-2}}{4 \times 10^{-2} – 2 \times 10^{-2}} \)
\(\displaystyle C = 4 \pi \times 8.854 \times 10^{-12} \frac{8 \times 10^{-4}}{2 \times 10^{-2}} \)
\(\displaystyle C = 4 \pi \times 8.854 \times 10^{-12} \times 4 \times 10^{-2} \)
\(\displaystyle C = 4 \times 3.1416 \times 8.854 \times 10^{-12} \times 4 \times 10^{-2} \)
\(\displaystyle C = 4 \times 3.1416 \times 8.854 \times 4 \times 10^{-14} \)
\(\displaystyle C = 1.11 \times 10^{-11} \, \text{F} \)

The energy (U) stored in the capacitor is:

\(\displaystyle U = \frac{1}{2} C V^2 \)
\(\displaystyle U = \frac{1}{2} \times 1.11 \times 10^{-11} \times (100)^2 \)
\(\displaystyle U = \frac{1}{2} \times 1.11 \times 10^{-11} \times 10^4 \)
\(\displaystyle U = 5.55 \times 10^{-8} \, \text{J} \)

Therefore, the energy stored in the spherical capacitor is (\(\displaystyle 5.55 \times 10^{-8} \, \text{J} \)).

Problem 6: Calculate the energy density at a point (r = 3 cm) from the center of a spherical capacitor with inner radius (r₁ = 2 cm) and outer radius (r₂ = 4 cm), charged to a potential difference of ( V = 100V).

Solution: The electric field (E) at a distance (r) from the center of a spherical capacitor is given by:

\(\displaystyle E = \frac{V}{r \ln(r_2/r_1)} \)

Calculate (E):

\(\displaystyle E = \frac{100}{3 \times 10^{-2} \ln(4/2)} \)
\(\displaystyle E = \frac{100}{3 \times 10^{-2} \ln(2)} \)
\(\displaystyle E = \frac{100}{3 \times 10^{-2} \times 0.693} \)
\(\displaystyle E = \frac{100}{0.02079} \)
\(\displaystyle E = 4809 \, \text{V/m} \)

The energy density (u) is given by:

\(\displaystyle u = \frac{1}{2} \epsilon_0 E^2 \)
\(\displaystyle u = \frac{1}{2} \times 8.854 \times 10^{-12} \times (4809)^2 \)
\(\displaystyle u = \frac{1}{2} \times 8.854 \times 10^{-12} \times 2.31 \times 10^7 \)
\(\displaystyle u = 1.02 \times 10^{-4} \, \text{J/m}^3 \)

Therefore, the energy density at a point (3 cm) from the center of the spherical capacitor is (\(\displaystyle 1.02 \times 10^{-4} \, \text{J/m}^3 \)).

FAQs