The concept of equilibrium in mechanics has been around since the time of Aristotle, but it was Isaac Newton who brought it into the realm of physics with his laws of motion. The idea is rooted in the search for conditions under which objects can exist in a state of balance or rest.
The concept of equilibrium is fundamental to understanding how objects behave when forces are applied to them. It’s a concept that dates back to ancient civilizations but was formalized in the scientific context during the Renaissance.
The earliest ideas of equilibrium can be traced back to the ancient Greeks. Philosophers like Aristotle pondered why objects stay at rest or move. However, their understanding was not based on the scientific method as we know it today.
It was during the Renaissance that scientists began to study equilibrium using the principles of mathematics and physics. Archimedes is a notable figure from this era; he studied levers and buoyancy, which are closely related to equilibrium.
The real breakthrough came with Sir Isaac Newton in the 17th century. His three laws of motion laid the groundwork for classical mechanics, including the concept of equilibrium. Newton’s first law, often called the law of inertia, states that an object will remain at rest or in uniform motion unless acted upon by an external force. This is essentially the definition of mechanical equilibrium for a particle.
Following Newton, the field of statics—the study of bodies at rest—evolved. Scientists and mathematicians like Leonhard Euler and Louis Lagrange developed equations that describe the conditions under which objects remain in equilibrium.
Today, the principles of equilibrium are applied in various fields, from engineering to architecture. Understanding how forces balance out is crucial for designing stable structures and machines.
Equilibrium Equations for Particles
When we talk about equilibrium in physics, we’re referring to a situation where all the forces acting on a particle balance out perfectly. An object is said to be in equilibrium when the forces acting upon it are balanced, meaning there is no net force causing it to move or change its state of motion. This means the particle is either at rest or moving with a constant velocity because there’s no net force causing it to accelerate.
To describe this state mathematically, we use what are known as the equilibrium equations for particles. These equations are based on Newton’s second law of motion, which states that the sum of the forces \(\displaystyle\sum \vec{F}\) acting on an object is equal to its mass (m) times its acceleration \(\displaystyle\vec{a}\):
\(\displaystyle\sum \vec{F} = m \vec{a}\)
For a particle in equilibrium, the acceleration (\(\displaystyle\vec{a}\)) is zero because, as we said, it’s either not moving or moving at a constant speed in a straight line. So, the equation simplifies to:
\(\displaystyle\sum \vec{F} = 0\)
This means that if you add up all the forces acting on the particle, they should cancel each other out, resulting in no net force.
To apply these equations, we usually break down the forces into their components along the x, y, and sometimes z axes (if we’re working in three dimensions). So, for a particle in equilibrium, the sum of the forces in each direction must be zero:
- In the x-direction: \(\displaystyle\sum F_{x} = 0 \)
- In the y-direction: \(\displaystyle\sum F_y = 0 \)
- In the z-direction (if applicable): \(\displaystyle\sum F_z = 0 \)
To find these forces, we often start by drawing a Free Body Diagram (FBD). This is a simple sketch where we represent the particle and all the different forces acting on it with arrows. Each arrow’s direction shows the force’s direction, and its length represents the force’s magnitude (how strong it is).
Once we have our FBD, we can write down the equilibrium equations based on the forces we’ve shown. If there are unknown forces or components, we can use these equations to solve for them, as long as we have enough information.
Example: Imagine a particle being pulled by two ropes in opposite directions. If one rope exerts a force of 10 N to the right and the other exerts a force of 10 N to the left, the particle is in equilibrium because the forces cancel each other out:
\(\displaystyle 10 \text{ N (right)} + 10 \text{ N (left)} = 0 \)
The equilibrium equations for particles are a set of mathematical conditions that express the balance of forces acting on a particle. When these conditions are met, the particle is in equilibrium, meaning it won’t accelerate.
Static Equilibrium
Static equilibrium specifically refers to objects at rest. For an object to be in static equilibrium, not only must the net force be zero, but the net torque (rotational force) must also be zero. This ensures the object does not rotate.

In simpler terms, it means that all the forces acting on the object are balanced, causing it to remain stationary. In static equilibrium, the object’s center of mass remains fixed, and there is no acceleration or change in its position or orientation.
Static equilibrium is characterized by the absence of any motion or tendency to move, as all the forces acting on the object or system are precisely balanced, resulting in a state of apparent rest.
Imagine you place a book on a table. The book exerts a downward force due to its weight, and the table exerts an equal and opposite force upward, known as the normal force. These two forces balance each other out vertically, preventing the book from falling through the table. This balance of forces in the vertical direction is an example of static equilibrium.
Additionally, there might be some friction between the book and the table, which opposes any tendency of the book to slide. If the book is not sliding, then the horizontal forces are also balanced, and the book remains in static equilibrium.
Static equilibrium occurs when an object is at rest and all the forces acting on it are balanced. This also means that the object is not accelerating in any direction.
The Conditions for Static Equilibrium: Two main conditions must be met for an object to be in static equilibrium:
Translational Equilibrium: The sum of all forces acting on the object must be zero. This is expressed as:
\(\displaystyle\sum \vec{F} = 0\)
In simpler terms, this means that if you push an object to the right with a certain force, there must be an equal force pushing it to the left to keep it in place.
Rotational Equilibrium: The sum of all torques (rotational forces) acting on the object must also be zero. This is expressed as:
\(\displaystyle\sum \vec{\tau} = 0\)
For example, if you’re turning a wrench, and someone else applies the same amount of turning force in the opposite direction, the wrench won’t rotate.
Understanding static equilibrium is crucial for engineers and architects. It helps them design buildings and structures that stay up without collapsing under their weight or the forces of nature like wind and earthquakes.
Static equilibrium is all about balance. It’s a state where everything is still, and no net force or torque is acting on an object.
Dynamic Equilibrium
Dynamic equilibrium is a state in which opposing forces or processes within a system are balanced, resulting in a constant overall state of motion or activity.
Unlike static equilibrium, where there is no motion at all, dynamic equilibrium involves continuous movement or change, but with the rates of opposing processes or forces remaining constant over time. In dynamic equilibrium, the system appears to be stable, despite ongoing activity, because the forward and backward processes or forces are occurring at the same rate, effectively canceling each other out.
Imagine you have a water tank with a pipe at the top pouring water into it continuously. At the same time, there’s a tap at the bottom of the tank allowing water to flow out.

As the tank fills up with water from the top, the water level increases, exerting more pressure on the bottom of the tank. This pressure pushes water out through the tap at the bottom. Similarly, as water flows out of the tank through the tap, it creates a suction effect, pulling more water down from the top.
Initially, the rate at which water flows into the tank from the top may exceed the rate at which it flows out from the tap, causing the water level to rise. However, as the water level rises, the pressure at the bottom of the tank increases, resulting in a faster flow rate out of the tap. Eventually, the flow rate out of the tap matches the flow rate into the tank from the top.
At this point, the system reaches dynamic equilibrium. Even though water is continuously being added to and removed from the tank, the rates of inflow and outflow are equal, resulting in a constant water level in the tank. In other words, the system is in a state of balance, with no net change in the amount of water in the tank over time.
Dynamic equilibrium, in this example, involves continuous movement or change (water flowing into and out of the tank), but with the rates of inflow and outflow remaining constant, resulting in a stable overall state.
For dynamic equilibrium to occur, two conditions must be met:
- No Net Force: The total forces pushing or pulling on an object must cancel each other out. This means the object won’t speed up or slow down.
- Constant Motion: The object must be moving at a constant speed in a straight line.
Think of a satellite orbiting Earth. Gravity pulls it towards the planet, but its forward motion keeps it from falling. The result is a constant orbit – a perfect example of dynamic equilibrium.
Dynamic equilibrium also applies to chemistry, where it describes a reversible reaction happening at a rate where the concentration of reactants and products remains constant over time. It’s like a dance where the number of dancers on the dance floor stays the same, even though some leave and others join in.
Understanding dynamic equilibrium helps us predict how objects will behave when they’re moving and when forces are applied to them. It’s a key concept for engineers designing vehicles and structures that need to remain stable under constant motion.
Dynamic equilibrium is all about balance in motion. It’s a state where everything looks calm, but there’s a delicate balance of forces that keeps things moving smoothly.
Also Read: Uniform Circular Motion
Finding the Equilibrium Equations
When we talk about finding the equilibrium equations, we’re essentially looking for a set of conditions that must be met for an object to be in equilibrium. This means the object is not accelerating, which implies it’s either at rest or moving at a constant velocity.
- Identify the Object: Determine which object or particle you’re analyzing for equilibrium.
- Draw a Free Body Diagram (FBD): Sketch the object and represent all the forces acting on it with arrows. Label each force clearly.
- Choose a Coordinate System: Decide on the orientation of your x, y, and (if necessary) z axes. This will help you break down forces into components.
- Resolve Forces into Components: Break down each force into its x and y components (and z components in 3D). Use trigonometry if the forces are at angles.
- Apply Newton’s First Law: For an object to be in equilibrium, the net force in each direction must be zero. Write down the equations for each direction:
In the x-direction: \(\displaystyle\sum F_{x} = 0 \)
In the y-direction: \(\displaystyle\sum F_{y} = 0 \)
In the z-direction (if in 3D): \(\displaystyle\sum F_{z} = 0 \)
Include Torque for Rotational Equilibrium: If the object can rotate, you must also ensure that the net torque is zero: \(\displaystyle \sum \tau = 0 \)
Solve the Equations: Use algebra to solve the set of equations for the unknowns. This could be the magnitude of forces, angles, or other quantities.
Example: A 9 kg traffic light is supported by two cables as shown below. Find the tension in each of the wires supporting the traffic light.
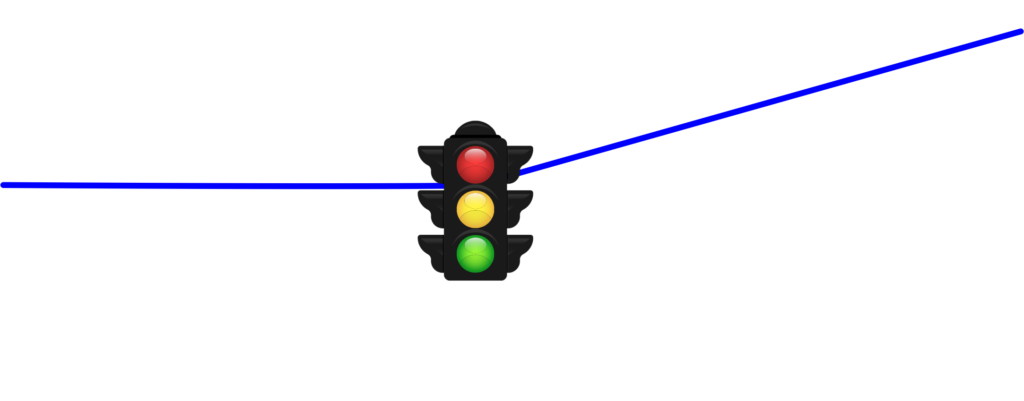
Answer: First, we draw a Free Body Diagram (FBD). This is a simple sketch where we represent the traffic light as a point and draw arrows to show the forces acting on it.
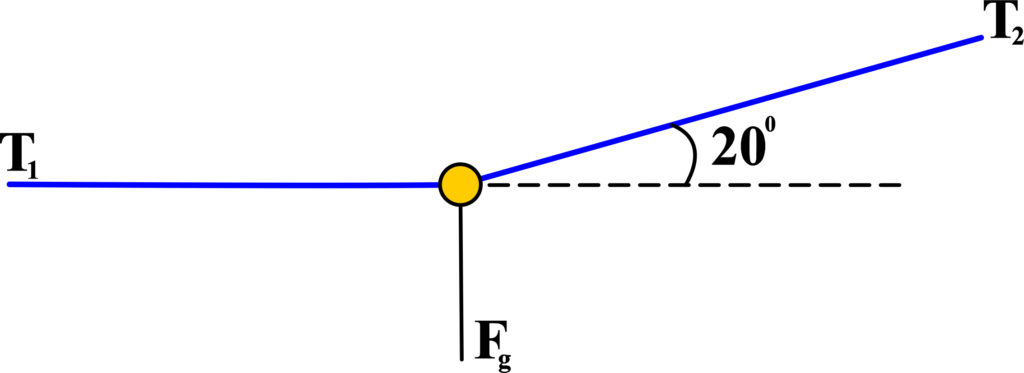
The weight of the traffic light pulls it down, while the tensions from the wires pull it up and to the sides.
We label the forces as (T1) and (T2) for the tensions from wire 1 and wire 2, respectively, and (W=Fg) for the weight of the traffic light.
\(\displaystyle \begin{array}{l}{{F}_{g}}=\left( {9.8} \right)\left( 9 \right)\\{{F}_{g}}=88.2N\end{array}\)
For an object to be in equilibrium, the forces must cancel out. So, we set up our equations:
\(\displaystyle \sum{{{{F}_{x}}}}=-{{T}_{1}}+{{T}_{2}}\cos ({{20}^{0}})=0\)
\(\displaystyle \sum{{{{F}_{y}}}}={{T}_{2}}\sin ({{20}^{0}})-88.2=0\)
These equations allow us to plug in known values and solve for the unknowns. If we know the weight of the traffic light, we can find the tension in the wires.
\(\displaystyle {{T}_{2}}=\frac{{88.2}}{{\sin \left( {{{{20}}^{0}}} \right)}}=287.89N\)
Now, plug in the values and solve for (T1):
\(\displaystyle \begin{array}{l}-{{T}_{1}}+257.89\cos \left( {{{{20}}^{0}}} \right)=0\\{{T}_{1}}=257.89\cos \left( {{{{20}}^{0}}} \right)\\{{T}_{1}}=\left( {257.89} \right)\left( {0.9397} \right)\\{{T}_{1}}=242.34\end{array}\)
So, the tension in each wire supporting the traffic light is approximately T1= 242.34 N and T2= 287.89 N.
Solved Examples
Problem 1: A block of mass 5 kg is placed on an inclined plane making an angle of 30° with the horizontal. The coefficient of static friction between the block and the plane is 0.5. Determine if the block remains at rest or slides down the plane.
Solution: First, resolve the forces acting on the block. The forces are: The component of gravitational force parallel to the plane is (\(\displaystyle mg \sin \theta\)).
The component of gravitational force perpendicular to the plane is (\(\displaystyle mg \cos \theta\)).
Given:
- (m = 5 kg)
- (g = 9.8 m/s2)
- (θ= 30∘)
- (µs = 0.5)
Calculate the forces:
\(\displaystyle mg \sin \theta = 5 \times 9.8 \times \sin 30^\circ = 5 \times 9.8 \times 0.5 = 24.5 \, \text{N} \)
\(\displaystyle mg \cos \theta = 5 \times 9.8 \times \cos 30^\circ = 5 \times 9.8 \times \frac{\sqrt{3}}{2} = 42.44 \, \text{N} \)
The maximum static frictional force is:
\(\displaystyle f_{\text{max}} = \mu_s N = \mu_s (mg \cos \theta) = 0.5 \times 42.44 = 21.22 \, \text{N} \)
Since (\(\displaystyle mg \sin \theta (24.5 \, \text{N}) > f_{\text{max}} (21.22 \, \text{N}) \)), the block will slide down the plane. The block will slide down the plane.
Problem 2: A 20 kg sign is hanging from the ceiling by two ropes, each making an angle of 45° with the horizontal. Find the tension in each rope.
Solution: In static equilibrium, the sum of forces in both x and y directions must be zero. Let ( T ) be the tension in each rope. Resolve the tensions into horizontal and vertical components:
- (\(\displaystyle T_x = T \cos 45^\circ \))
- (\(\displaystyle T_y = T \sin 45^\circ \))
The weight of the sign acts downward:
\(\displaystyle mg = 20 \times 9.8 = 196 \, \text{N} \)
For vertical equilibrium:
\(\displaystyle 2T \sin 45^\circ = mg \)
\(\displaystyle 2T \times \frac{\sqrt{2}}{2} = 196 \)
\(\displaystyle T \sqrt{2} = 196 \)
\(\displaystyle T = \frac{196}{\sqrt{2}} = 138.6 \, \text{N} \)
The tension in each rope is 138.6 N.
Problem 3: A particle is in equilibrium under the action of three forces: (\(\displaystyle \vec{F}_1 = 3\hat{i} + 4\hat{j} – 5\hat{k} \, \text{N}\) ), (\(\displaystyle \vec{F}_2 = -2\hat{i} + 2\hat{j} + 3\hat{k} \, \text{N} \)), and (\(\displaystyle \vec{F}_3 ). Determine ( \vec{F}_3 \)).
Solution: In equilibrium, the sum of all forces acting on the particle must be zero:
\(\displaystyle \vec{F}_1 + \vec{F}_2 + \vec{F}_3 = 0 \)
\(\displaystyle (3\hat{i} + 4\hat{j} – 5\hat{k}) + (-2\hat{i} + 2\hat{j} + 3\hat{k}) + \vec{F}_3 = 0\)
Combine the forces:
\(\displaystyle (3 – 2)\hat{i} + (4 + 2)\hat{j} + (-5 + 3)\hat{k} + \vec{F}_3 = 0 \)
\(\displaystyle 1\hat{i} + 6\hat{j} – 2\hat{k} + \vec{F}_3 = 0 \)
Therefore, ( \(\displaystyle\vec{F}_3 = -1\hat{i} – 6\hat{j} + 2\hat{k} \, \text{N} \)).
Problem 4: A 10 kg block is pushed along a frictionless horizontal surface with a force of 50 N. What is the acceleration of the block?
Solution: In dynamic equilibrium (steady motion with constant velocity), the net force on the block must be zero. However, in this case, we are interested in the acceleration, not static equilibrium.
Using Newton’s second law:
\(\displaystyle F = ma \)
Given: F = 50 N; m = 10 kg.
\(\displaystyle a = \frac{F}{m} = \frac{50}{10} = 5 \, \text{m/s}^2 \)
The acceleration of the block is (5 m/s2).
Problem 5: A 15 kg ladder 4 meters long rests against a smooth vertical wall at an angle of 60° with the horizontal. Find the force exerted by the wall on the ladder.
Solution: In static equilibrium, the sum of torques around any point must be zero. Let (N) be the normal force exerted by the wall, and (Ff) be the frictional force at the ground.
Taking torques around the base of the ladder:
\(\displaystyle N \times 4 \sin 60^\circ = mg \times 2 \cos 60^\circ \)
Given: m = 15 kg; g = 9.8 m/s2; θ = 60∘
\(\displaystyle N \times 4 \times \frac{\sqrt{3}}{2} = 15 \times 9.8 \times 2 \times \frac{1}{2} \)
\(\displaystyle N \times 2\sqrt{3} = 15 \times 9.8 \)
\(\displaystyle N \times 2\sqrt{3} = 147 \)
\(\displaystyle N = \frac{147}{2\sqrt{3}} = \frac{147}{2 \times 1.732} = 42.5 \, \text{N} \)
The force exerted by the wall on the ladder is 42.5 N.
Problem 6: A uniform beam of length 10 m and weight 200 N is supported at its ends. A 300 N weight is placed 3 m from the left end. Find the reactions at the supports.
Solution: Let (RA) and (RB) be the reactions at the left and right supports, respectively.
Using the equilibrium conditions:
\(\displaystyle R_A + R_B = 200 + 300 = 500 \, \text{N} \)
Taking moments about the left end:
\(\displaystyle R_B \times 10 = 200 \times 5 + 300 \times 3\)
\(\displaystyle R_B \times 10 = 1000 + 900 \)
\(\displaystyle R_B \times 10 = 1900\)
RB = 190 N
Substitute (RB) into the first equation:
\(\displaystyle R_A + 190 = 500 \)
RA = 310 N
The reactions at the supports are (RA = 310 N) and (RB = 190 N).
FAQs
What does it mean for a particle to be in equilibrium?
A particle is in equilibrium when the net force acting on it is zero, and consequently, the particle remains at rest or moves with constant velocity. In other words, the forces acting on the particle are balanced, resulting in no acceleration.
How does the concept of equilibrium apply to real-life scenarios?
Equilibrium is observed in various real-life situations, such as a book resting on a table or a bridge structure supporting the weight of vehicles. In these cases, the forces acting on the objects are balanced, preventing any motion or deformation.
Can a particle be in equilibrium even if it’s moving?
Yes, a particle can be in equilibrium even if it’s moving at a constant velocity. This is known as dynamic equilibrium, where the forces acting on the particle are balanced, resulting in zero acceleration. An example of dynamic equilibrium is a car moving at a constant speed along a straight road.
How can we determine if a particle is in equilibrium mathematically?
To determine if a particle is in equilibrium mathematically, we analyze the forces acting on the particle using vector addition. If the vector sum of all the forces acting on the particle is zero, the particle is in equilibrium. This can be expressed mathematically as ΣF = 0, where ΣF represents the vector sum of all the forces.
Can a particle be in equilibrium if it’s subjected to non-concurrent forces?
Yes, a particle can be in equilibrium even if it’s subjected to non-concurrent forces. In such cases, we apply the principle of moments or torque equilibrium. If the vector sum of the moments of all the forces about any point is zero, the particle is in equilibrium, regardless of whether the forces are concurrent or non-concurrent.
How does the concept of equilibrium extend to three-dimensional systems?
In three-dimensional systems, the concept of equilibrium still applies, but we consider forces and moments acting in multiple directions. Equilibrium is achieved when the vector sum of all the forces and the vector sum of all the moments about any point are both zero.
Can you provide an example of equilibrium in a complex mechanical system?
One example of equilibrium in a complex mechanical system is a suspension bridge. The cables and support structures of the bridge are designed to distribute the weight of vehicles evenly, ensuring that the forces acting on the bridge are balanced. This equilibrium allows the bridge to support heavy loads without collapsing.