The concept of a frame of reference is like the backdrop of a theater stage—it sets the scene for where and how we observe motion and forces. The idea of a frame of reference has existed since ancient times, but it wasn’t formally defined until much later. Ancient astronomers used the stars as a fixed point of reference to measure the movement of planets.
In the 17th century, Galileo Galilei introduced the idea that the laws of physics are the same in any frame of reference that is moving at a constant speed in a straight line, which he called an “inertial frame of reference.” This was a revolutionary idea because it meant that there was no single, absolute frame of reference.
Isaac Newton built on Galileo’s ideas and formulated his laws of motion, which are based on inertial frames of reference. Newton’s laws provided a way to describe motion and forces from different perspectives, whether standing still or moving at a constant velocity.
The next big leap came from Albert Einstein in the early 20th century. His theory of relativity showed that the laws of physics are the same for all observers, no matter how they are moving relative to each other, as long as they are not accelerating. This expanded the concept of a frame of reference to include many perspectives.
Today, the concept of a frame of reference is fundamental in physics. It helps us understand complex ideas like the motion of satellites, the flow of rivers, and even the expansion of the universe.
What is a frame of Reference?
The concept of a frame of reference is fundamental in physics, and it has evolved as our understanding of the universe has grown. Initially, the idea of a frame of reference wasn’t clearly defined. Ancient astronomers like Ptolemy used Earth as the central point (geocentric model) to explain the motion of celestial bodies. Later, Copernicus proposed a heliocentric model with the Sun at the center, which was a shift in the frame of reference for understanding planetary motion.
Isaac Newton revolutionized the concept by introducing an ‘absolute space’ in his laws of motion, which provided a fixed frame of reference from which to measure all motion. However, Newton also acknowledged that many problems in mechanics could be solved by using any frame of reference that was either at rest or moving uniformly straight, leading to the concept of ‘inertial frames of reference’.
The most significant advancement came from Albert Einstein. In his theory of special relativity, he showed that the laws of physics are the same in all inertial frames of reference, but the way we measure distances and time can change depending on the frame’s relative motion. This led to the idea that there is no single ‘absolute’ frame of reference – all motion is relative to the observer’s frame of reference.
Today, in modern physics, frames of reference are used to describe the motion of particles in fields as diverse as quantum mechanics and cosmology. The choice of frame can simplify problems and reveal symmetries that are not apparent in other frames.
The history of the frame of reference shows us how our perspective on motion and the universe has changed. It’s like watching a play from different seats in a theater; depending on where you sit, you’ll see the play from a unique angle, but the play itself remains the same. Similarly, the frame of reference provides us with different ‘views’ of the same physical phenomena.
Frame of Reference in Kinematics
A frame of reference in kinematics is like a stage on which all motion is observed and measured. It consists of an abstract coordinate system that allows us to describe the position, velocity, and acceleration of objects. Just as a painter needs a canvas to paint a picture, physicists need a frame of reference to describe motion. Without it, we can’t accurately say how fast something is moving or in which direction.
A frame of reference in kinematics is essentially a viewpoint or a set of guidelines that we use to measure and describe the motion of objects. It’s like having a ruler and a compass that help us map out where things are and how they’re moving.
Without a frame of reference, we can’t accurately describe the motion of anything because motion is always relative. For example, if you’re sitting in a moving train, you might feel like you’re not moving, but to someone outside, you’re moving quite fast. The frame of reference helps us agree on how we’re seeing and measuring movement.
In kinematics, we often use a coordinate system as our frame of reference. This could be a simple set of axes on graph paper or a more complex system like GPS coordinates. It gives us a common language to describe positions, speeds, and accelerations.
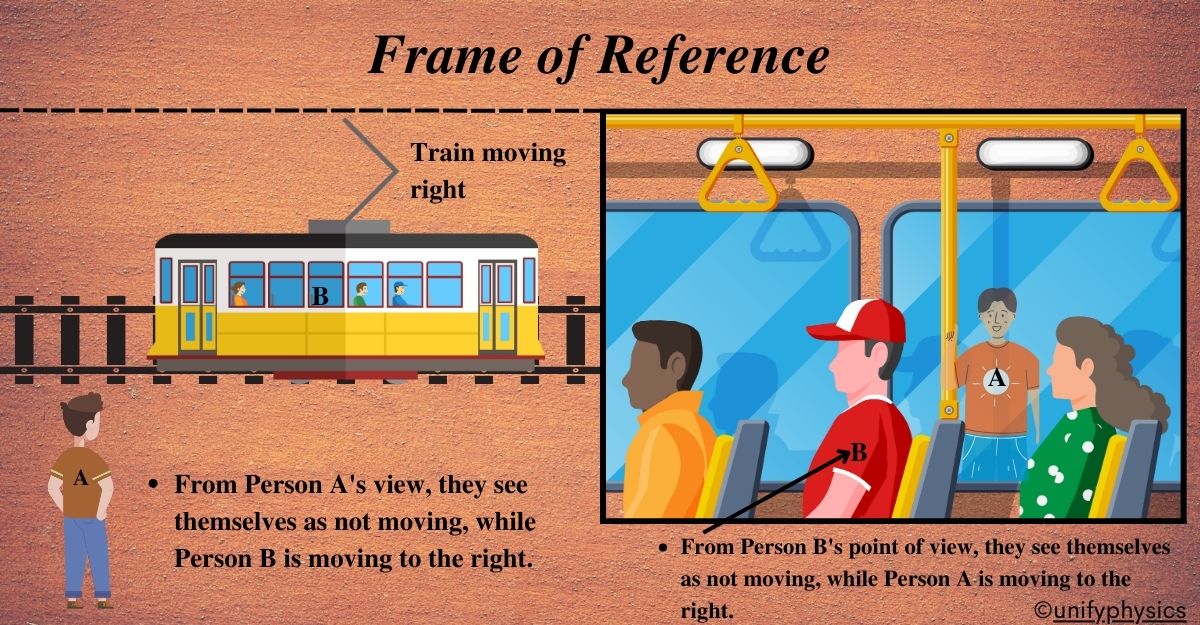
Example: Imagine you’re sitting on a train that’s moving at a steady speed. You look outside and see trees, buildings, and other trains moving past you. Now, let’s think about this scenario from different perspectives:
From Your Perspective Inside the Train: To you, it might seem like you’re stationary and everything outside is moving backward. This is because your frame of reference is the train itself, which is moving at a constant speed. In this frame of reference, you could say that you are at rest.

From an Observer on the Ground: Now, consider someone standing on the platform as the train zooms by. To them, you’re moving at the same speed as the train. Their frame of reference is the ground, which is stationary relative to the moving train. In this frame of reference, you and the train are moving forward.
This example shows that motion is relative. Your perception of motion changes depending on your frame of reference. In kinematics, which is the study of motion without considering forces, defining a frame of reference is crucial because it allows us to describe and calculate the motion of objects consistently and accurately.
Also Read: Laws Of Motion
Types of Frames of Reference
Once we have chosen our reference they can be of two types:
- Inertial Frames: These are ‘non-accelerating’ frames. If you’re in an inertial frame, objects will either stay still or move at a constant speed in a straight line unless a force acts on them.
- Non-Inertial Frames: These frames are accelerating. If you’re in a non-inertial frame, like a car that’s braking or turning, you’ll feel forces (like being pushed into your seat) that don’t exist in inertial frames.
Inertial Frame of Reference
An inertial frame of reference is one where an object remains at rest or moves at a constant velocity unless acted upon by an external force. It’s like sitting in a car that’s moving at a steady speed – inside the car, you feel like you’re not moving or It’s like watching a game from a steady camera; the players may move, but the camera stays still or moves at a constant speed in a straight line.
Characteristics:
- Newton’s First Law Applies: In an inertial frame, objects at rest stay at rest, and objects in motion stay in motion at a constant velocity unless acted upon by a net external force.
- No Acceleration: There’s no acceleration in an inertial frame, meaning no speeding up, slowing down, or changing direction.
- Simplifies Physics: Many physics problems are easier to solve when using an inertial frame because the behavior of objects is more predictable.
In physics, especially in mechanics, we often choose an inertial frame of reference to describe the motion of objects because it aligns with our intuitive understanding of motion. It’s the ‘default’ setting for applying Newton’s laws.
While no perfect inertial frame exists due to the gravitational pull of celestial bodies, we often treat Earth as an inertial frame for practical purposes, except when dealing with very high speeds or large-scale astronomical phenomena. An inertial frame of reference is a stable and non-accelerating viewpoint that allows us to apply Newton’s laws of motion consistently.
Non-inertial Frame of Reference
A non-inertial frame of reference is accelerating. If you’re in a car that’s speeding up, slowing down, or turning, you’re in a non-inertial frame because you can feel the change in motion.
A non-inertial frame of reference is a viewpoint in which you feel forces that are not caused by any physical interaction with other objects. These are called fictitious or pseudo forces because they arise due to the acceleration of the frame itself.
Characteristics:
- Acceleration: Unlike inertial frames, non-inertial frames are accelerating, which means they can speed up, slow down, or change direction.
- Pseudo Forces: In these frames, we introduce pseudo forces to explain the motion of objects. For example, when you’re in a car that suddenly stops, you feel like you’re being thrown forward. This is due to a pseudo force because the car’s frame of reference is decelerating.
Why Use Non-inertial Frames? : Sometimes it’s more convenient to describe motion from a non-inertial frame. For instance, when analyzing the motion of a pendulum in a car, it’s easier to consider the car (which is accelerating) as the frame of reference and account for the car’s acceleration when predicting the pendulum’s motion.
Think about being on a merry-go-round. To someone standing outside (in an inertial frame), you’re moving in a circle. But from your perspective (in a non-inertial frame), it feels like there’s a force pushing you outward, away from the center. This is the centrifugal force, a type of pseudo force.
Non-inertial frames of reference are essential when the observer is accelerating. They help us understand and predict how objects will move relative to that accelerating frame by introducing additional forces to account for the acceleration. It’s a bit like trying to walk on a moving bus; you have to adjust your balance for the bus’s movements, which is the effect of being in a non-inertial frame.
Solved Examples
Problem 1: A car A is moving with a velocity of 60 km/h due east, and car B is moving with a velocity of 45 km/h due west. What is the velocity of car A relative to car B?
Solution: Relative velocity is calculated as:
\(\displaystyle \vec{v}_{A/B} = \vec{v}_A – \vec{v}_B \)
Given:
- (\(\displaystyle\vec{v}_A = 60 \, \text{km/h}\) ) (east)
- (\(\displaystyle\vec{v}_B = -45 \, \text{km/h} ) (west, taken as negative\))
Substituting the values:
\(\displaystyle \vec{v}{A/B} = 60 – (-45) ] [ \vec{v}{A/B} = 60 + 45 \)
\(\displaystyle \vec{v}_{A/B} = 105 \, \text{km/h} \)
The velocity of car A relative to car B is 105 km/h due east.
Problem 2: A boat is moving due north at 5 m/s, and the river current is flowing due east at 3 m/s. What is the resultant velocity of the boat relative to the ground?
Solution: We use vector addition to find the resultant velocity:
\(\displaystyle \vec{v}{\text{resultant}} = \vec{v}{\text{boat}} + \vec{v}_{\text{current}} \)
Given:
- (\(\displaystyle\vec{v}_{\text{boat}} = 5 \, \text{m/s} \, \hat{j}\))
- (\(\displaystyle\vec{v}_{\text{current}} = 3 \, \text{m/s} \, \hat{i}\))
The resultant velocity is:
\(\displaystyle \vec{v}_{\text{resultant}} = 5 \, \hat{j} + 3 \, \hat{i} \)
Magnitude of (\vec{v}{\text{resultant}}):
\(\displaystyle |\vec{v}{\text{resultant}}| = \sqrt{(5)^2 + (3)^2} \)
\(\displaystyle |\vec{v}{\text{resultant}}| = \sqrt{25 + 9} \)
\(\displaystyle |\vec{v}{\text{resultant}}| = \sqrt{34} \)
\(\displaystyle |\vec{v}_{\text{resultant}}| \approx 5.83 \, \text{m/s} \)
Direction (angle (θ)) with respect to east:
\(\displaystyle \theta = \tan^{-1}\left(\frac{5}{3}\right) \)
\(\displaystyle\theta = \tan^{-1}\left(\frac{5}{3}\right) \approx 59.04^\circ \)
The resultant velocity of the boat relative to the ground is approximately 5.83 m/s at an angle of 59.04° north of east.
Problem 3: A passenger on a train moving at 72 km/h due east walks towards the front of the train at 3 km/h. What is the speed of the passenger relative to a stationary observer on the ground?
Solution: Relative velocity is calculated as:
\(\displaystyle \vec{v}{\text{passenger/ground}} = \vec{v}{\text{train}} + \vec{v}_{\text{passenger/train}} \)
Given:
- (\(\displaystyle\vec{v}_{\text{train}} = 72 \, \text{km/h} \, \text{east}\) )
- (\(\displaystyle\vec{v}_{\text{passenger/train}} = 3 \, \text{km/h} \, \text{east} \))
Substituting the values:
\(\displaystyle \vec{v}{\text{passenger/ground}} = 72 + 3 \)
\(\displaystyle \vec{v}{\text{passenger/ground}} = 75 \, \text{km/h} \)
The speed of the passenger relative to a stationary observer on the ground is 75 km/h due east.
Problem 4: A car is accelerating uniformly at (2 m/s2) to the right. Inside the car, a pendulum hangs from the ceiling. What angle (θ) does the pendulum make with the vertical?
Solution: In the non-inertial frame of the accelerating car, a fictitious force acts to the left. The pendulum reaches equilibrium when the tension (T) in the string provides the necessary centripetal force.
The forces in the x and y directions are:
\(\displaystyle T \sin \theta = m a \)
\(\displaystyle T \cos \theta = mg \)
Taking the ratio:
\(\displaystyle \tan \theta = \frac{a}{g} \)
Given:
- (a = 2 m/s2)
- (g = 9.8 m/s2)
\(\displaystyle \theta = \tan^{-1}\left(\frac{2}{9.8}\right) \)
\(\displaystyle \theta = \tan^{-1}\left(0.204\right) \)
\(\displaystyle\theta \approx 11.53^\circ \)
The pendulum makes an angle of approximately 11.53° with the vertical.
Problem 5: A person of mass 70 kg is standing in an elevator accelerating upward at (3 m/s2). What is the apparent weight of the person?
Solution: The apparent weight (W’) is given by:
\(\displaystyle W’ = m (g + a) \)
Given:
- (m = 70 kg)
- (g = 9.8 m/s2)
- (a = 3 m/s2)
Substituting the values:
\(\displaystyle W’ = 70 \times (9.8 + 3) ]
\)latex \displaystyle W’ = 70 \times 12.8 ]
W’ = 896 N
The apparent weight of the person is 896 N.
Problem 6: Calculate the apparent weight of a 60 kg person standing at the equator, where the rotation of the Earth causes a centripetal acceleration of (0.034 m/s2).
Solution: The apparent weight (W’) is given by:
\(\displaystyle W’ = m (g – a_{\text{centripetal}}) \)
Given:
- (m = 60 kg)
- (g = 9.8 m/s2)
- (\(\displaystyle a_{\text{centripetal}} = 0.034 \, \text{m/s}^2\))
Substituting the values:
\(\displaystyle W’ = 60 \times (9.8 – 0.034) \)
\(\displaystyle W’ = 60 \times 9.766 \)
W’ = 585.96 N
The apparent weight of the person at the equator is 585.96 N.
FAQs
How does the choice of frame of reference impact the observation of motion?
The choice of frame of reference affects how we perceive motion. In one frame, an object might appear stationary, while in another, it might seem to be in motion. This highlights the relative nature of motion and the importance of selecting an appropriate frame for analysis.
Can you provide an example where understanding frames of reference is crucial in real-life scenarios?
Imagine you’re on a moving train, and you toss a ball vertically upward. To you, it appears to travel in a straight line, but to an observer on the platform, it follows a curved path due to the train’s motion. This demonstrates how different frames offer contrasting perspectives on the same event.
How do inertial and non-inertial frames of reference differ?
Inertial frames move at a constant velocity, while non-inertial frames accelerate. Newton’s first law holds true in inertial frames, whereas in non-inertial frames, fictitious forces like centrifugal force might need to be considered to describe motion accurately.
Can you explain how frames of reference relate to Einstein’s theory of relativity?
Einstein’s theory of relativity suggests that all inertial frames are equally valid for describing physical phenomena. It challenges the absolute nature of space and time, emphasizing that measurements depend on the observer’s relative motion. This revolutionized our understanding of frames of reference and the concept of simultaneity.
Is there a preferred frame of reference in physics?
No, there isn’t a preferred frame of reference in physics. The laws of physics remain consistent across all inertial frames, so choosing a frame depends on convenience and simplicity for a particular problem. However, certain frames may offer clearer insights into specific phenomena.
How do astronomers use different frames of reference to describe celestial motion?
Astronomers often use heliocentric and geocentric frames of reference to describe celestial motion. In the heliocentric frame, the sun is stationary, and planets orbit around it, while in the geocentric frame, the Earth is considered the center. Each frame offers unique insights into planetary motion.
Are there any practical applications of understanding frames of reference outside of physics?
Yes, understanding frames of reference is crucial in various fields, including engineering, navigation, and robotics. Engineers use different frames to analyze the motion of vehicles, aircraft, and structures, while GPS navigation relies on a precise understanding of reference frames for accurate positioning. Similarly, robotics often coordinate motion relative to different reference points for efficient operation.