The story of Gauss’s Law begins with Joseph-Louis Lagrange in 1773, who first formulated the law in the context of the attraction of ellipsoids. However, it was Carl Friedrich Gauss who, in 1835, brought the law to prominence in the field of electromagnetism.
Gauss’s Law, also known as Gauss’s flux theorem, is one of the four Maxwell’s equations that form the foundation of classical electrodynamics. These equations describe how electric and magnetic fields are generated and altered by each other and by charges and currents.
Gauss himself used the law to relate the distribution of electric charge to the resulting electric field. This was a significant step forward because it provided a method to calculate the electric field in various situations, especially those involving symmetrical charge distributions. Gauss’s Law is a cornerstone of electromagnetism and has been instrumental in advancing our understanding of electric fields and forces.
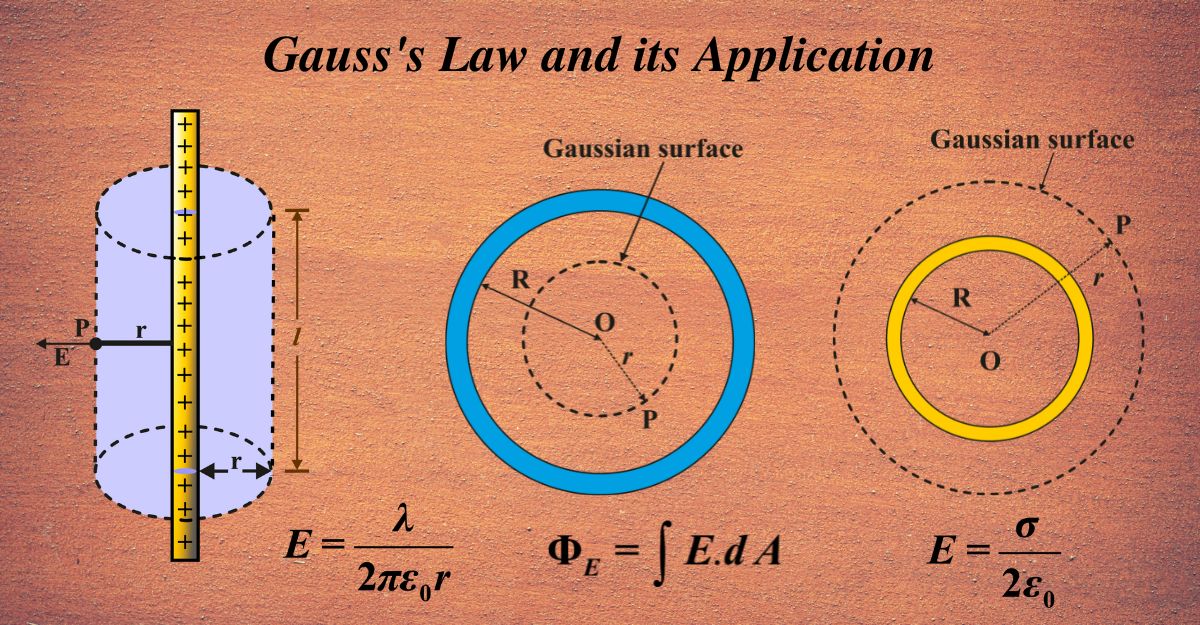
What is Gauss’s Law?
Gauss’s Law states that the electric flux through any closed surface is proportional to the enclosed electric charge, irrespective of how that charge is distributed. This principle can be applied to derive Coulomb’s law, which describes the force between two point charges, and vice versa.
Imagine you have a net and you’re trying to catch fish in a pond. The number of fish you catch depends on two things: how many fish are in the pond and the size of your net. Gauss’s Law works similarly for electric fields and charges.
In technical terms, Gauss’s Law is about the relationship between electric charges and the electric field they produce. It says that the total electric flux (think of it as the number of electric field lines) passing through a closed surface (like an invisible net) is directly related to the amount of charge enclosed within that surface.
Here’s the simple formula for Gauss’s Law:
\(\displaystyle \Phi_E = \frac{Q_{enc}}{\varepsilon_0} \)
- (ΦE) is the electric flux through the surface.
- (Qenc) is the total charge enclosed by the surface.
- ∈0) is the permittivity of free space, a constant that measures how electric fields interact with the vacuum.
To understand this better, let’s say you have a closed box, and inside the box, you have some positive charges. Gauss’s Law tells us that if we count the number of electric field lines going out of the box (the electric flux), it will tell us how much charge is inside the box. It doesn’t matter where the charges are located inside the box or what shape the box is; the law still applies.
Gauss’s Law is super handy because it lets us calculate electric fields easily when we have symmetrical situations, like a sphere, cylinder, or plane. It’s like having a shortcut instead of measuring the field at every point around the charge.
So, when you think of Gauss’s Law, remember the fishnet analogy: the electric flux through your net tells you about the charges inside, just like the number of fish you catch tells you about the fish in the pond. It’s a simple yet profound law that connects the invisible world of electric fields to the tangible reality of electric charges.
The Gauss Theorem
The Gauss Theorem is another name for Gauss’s Law. It’s a theorem stating the relationship between electric charges and electric field lines.
Think of Gauss’s Theorem as a cosmic balance sheet that accounts for all the electric field lines entering and leaving a closed space. It’s a bit like checking how many people enter and leave a party to figure out how many are inside.

- Electric Flux: This is the total number of electric field lines passing through a surface. Imagine it as the amount of ‘electric flow’ through a net.
- Closed Surface: This is an imaginary boundary that you draw around a charge or group of charges. It can be any shape: a sphere, a cube, or even a donut!
Now, Gauss’s Theorem states: The total electric flux through a closed surface is directly proportional to the total charge enclosed within that surface.
Mathematically, it’s written as:
\(\displaystyle \oint \vec{E} \cdot d\vec{A} = \frac{Q_{enc}}{\varepsilon_0} \)
Here, (\(\displaystyle \oint \vec{E} \cdot d\vec{A}\) ) represents the total electric flux through the surface, (Qenc) is the charge enclosed, and (\(\displaystyle \varepsilon_0 \)) is the permittivity of free space.
Imagine you have a bubble wand and you’re blowing bubbles (our closed surface). Inside each bubble, you place some tiny charged particles. Gauss’s Theorem helps us count how many electric field lines are coming out of the bubble based on how many charged particles are inside, without popping the bubble!
Key Points:
- Symmetry is Your Friend: Gauss’s Theorem is super powerful in symmetrical situations. If the charges are spread out evenly, like on a sphere, it makes calculating the electric field a breeze.
- It’s All About the Net Flow: Just like a net cash flow in accounting, Gauss’s Theorem is about the net electric flux. Some field lines might enter, some might leave, but it’s the total count that matters.
- Charges Outside Don’t Count: Charges outside your imaginary bubble don’t affect the electric flux inside it. They’re like party crashers who can’t get past the bouncer.
In simple terms, Gauss’s Theorem is a fundamental principle in physics that relates the electric field lines passing through a closed surface to the charge contained within it.
Proof of Gauss Theorem
Gauss’s Theorem is all about the relationship between electric charges and the electric field they produce. To prove it, we’ll use a simple and symmetrical situation: a spherical surface surrounding a single-point charge.
First, we choose a Gaussian surface. For a point charge, the best choice is a sphere centered on the charge because the electric field is the same at every point on the surface. The electric field due to a point charge (q) at a distance (r) from the charge is given by Coulomb’s law:
\(\displaystyle E = \frac{k \cdot q}{r^2} \)
where (k) is Coulomb’s constant.
Electric flux (Φ) through a surface is the electric field (E) times the area (A) of the surface perpendicular to the field. For our sphere, the area is (\(\displaystyle 4\pi r^2 \)), so the flux is:
\(\displaystyle Φ = E \cdot A = \frac{k \cdot q}{r^2} \cdot 4\pi r^2 = 4\pi k \cdot q \)
Coulomb’s constant (k) is related to the permittivity of free space (ε₀) by:
\(\displaystyle k = \frac{1}{4\pi \varepsilon_0} \)
Substituting (k) in the flux equation gives us:
\(\displaystyle Φ = \frac{q}{\varepsilon_0} \)
The beauty of Gauss’s Theorem is that it doesn’t just work for spheres. No matter the shape of the closed surface, as long as it encloses the charge, the total electric flux through the surface will be the same. This is because electric field lines are continuous and must begin and end on charges, so all lines emanating from our enclosed charge must pass through the surface.
The total electric flux (Φ) through any closed surface surrounding a charge (q) is equal to the charge divided by the permittivity of free space (ε₀). This is Gauss’s Theorem, and it’s written as:
\(\displaystyle \Phi = \frac{q}{\varepsilon_0} \)
This theorem is incredibly useful because it simplifies the calculation of electric fields, especially in symmetrical situations.
Corollary of the Gauss Theorem
A corollary is like a bonus fact that comes out of a theorem. In the case of Gauss’s Theorem, one of the most interesting corollaries is about the behavior of electric fields in conductors.
The corollary states that the electric field inside a conductor at equilibrium is zero. This might sound a bit surprising at first, but here’s why it makes sense:
- Conductors have free charges (like electrons) that can move around easily.
- When you put a conductor in an electric field, these free charges will start to move.
- They’ll keep moving until they’ve canceled out the electric field inside the conductor completely.
Think of it like a group of friends trying to balance on a seesaw. They’ll shuffle around until they’re perfectly balanced and the seesaw is level. In the same way, charges in a conductor move until they’ve balanced out the electric field.
Since the electric field inside the conductor is zero, any excess charge will be found on the surface of the conductor. Right outside the surface of a charged conductor, the electric field is perpendicular to the surface. This is because the charges on the surface create an electric field that points directly away from (or toward) the surface.
In simple terms, If you’re inside a metal sphere, no matter how much charge is on the outside, you won’t feel any electric field. It’s like being in the eye of a storm—calm and quiet, even if there’s chaos outside.
Application of Gauss Theorem
The application of Gauss’s Law extends to a myriad of practical situations, ranging from the behavior of charged conductors to the determination of electric fields around uniformly charged objects.
Field due to an infinitely long straight uniformly charged wire
Consider a very long wire that’s charged uniformly. We want to find out the electric field it creates around it. For a long straight wire, we choose a cylindrical surface around the wire as our Gaussian surface. This is because the symmetry of the problem suggests that the electric field at any point around the wire will be the same at a given distance from the wire.
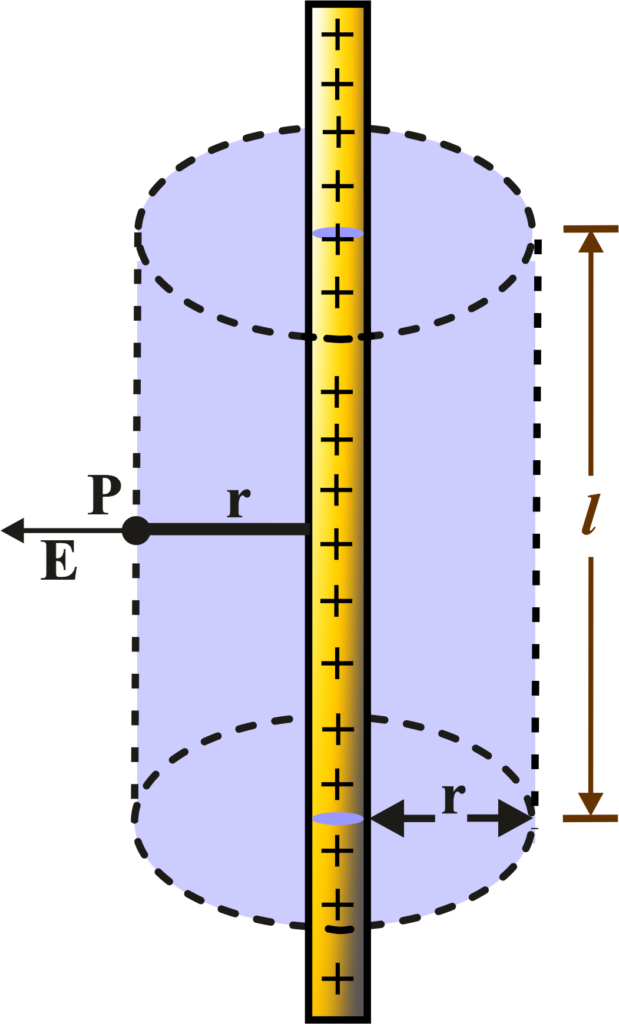
Due to the wire’s uniform charge and infinite length, the electric field has to point radially outward (or inward if the charge is negative) and be the same at any point equidistant from the wire.
Now, we apply Gauss’s Law, which tells us that the total electric flux through the cylindrical surface is equal to the charge enclosed divided by the permittivity of free space (∊0).
If (λ) is the charge per unit length of the wire, and (l) is the length of our cylindrical Gaussian surface, then the total charge enclosed is (\(\displaystyle \lambda \cdot l \)).
The electric flux is the electric field (E) times the area of the curved surface of the cylinder
\(\displaystyle A = 2\pi r l \),
where (r) is the radius of the cylinder. Putting it all together, we get:
\(\displaystyle \Phi_E = E \cdot A = E \cdot 2\pi r l \)
According to Gauss’s Law:
\(\displaystyle \Phi_E = \frac{\lambda \cdot l}{\varepsilon_0} \)
Equating the two expressions for (ΦE) and solving for (E) gives us:
\(\displaystyle E \cdot 2\pi r l = \frac{\lambda \cdot l}{\varepsilon_0} \)
\(\displaystyle E = \frac{\lambda}{2\pi r \varepsilon_0} \)
The electric field (E) at a distance (r) from an infinitely long, uniformly charged wire is inversely proportional to r. It decreases as you move away from the wire and increases as you get closer.
Field due to a uniformly charged infinite plane sheet
Consider an infinitely large, thin sheet that’s uniformly charged. This means the charge is spread out evenly across the entire sheet.
To apply Gauss’s Theorem, we need to choose a Gaussian surface. A good choice for an infinite plane sheet is a cylindrical Gaussian surface that intersects the sheet perpendicularly. Why a cylinder? Because of its symmetry and the fact that it has two flat ends that are parallel to the sheet.
Due to the uniform charge and the infinite size of the sheet, the electric field at any point near the sheet is the same. It points directly away from the sheet if the charge is positive, and towards the sheet if it is negative.
The electric flux through the cylindrical surface is only through the flat ends because the sides are parallel to the field lines, and thus, no lines pass through them. If (E) is the electric field and (A) is the area of each end, the total flux (Φ) through the cylinder is (Φ = 2EA) (since there are two ends).
Gauss’s Law tells us that this flux is equal to the charge enclosed divided by the permittivity of free space (\(\displaystyle\varepsilon_0 \)). If (σ) is the surface charge density of the sheet, then the charge enclosed by our cylinder is (σA ).
Now, we can write Gauss’s Law as:
\(\displaystyle \Phi = \frac{\sigma A}{\varepsilon_0} \)
Equating the two expressions for (Φ) gives us:
\(\displaystyle 2EA = \frac{\sigma A}{\varepsilon_0} \)
\(\displaystyle E = \frac{\sigma}{2\varepsilon_0} \)
The electric field (E) due to a uniformly charged infinite plane sheet is constant and does not depend on the distance from the sheet. It’s always pointing directly away from (or towards) the sheet, and its magnitude is determined by the surface charge density (σ).
Field due to a uniformly charged thin spherical shell
Let us consider a thin spherical shell of radius R and total charge Q, which is uniformly distributed over the surface. We want to find the electric field at any point P, which is at a distance r from the center of the shell.
(a) Field Outside The Shell (r > R)
For a point outside the shell, we choose a spherical Gaussian surface with radius (r) such that (r > R). This surface is concentric with the charged shell. Due to the symmetry of the spherical shell, the electric field (E) at any point on the Gaussian surface is the same and points radially outward from the center of the shell.

The electric flux (Φ) through the Gaussian surface is the product of the electric field (E) and the surface area (A) of the Gaussian surface:
\(\displaystyle \Phi = E \cdot A = E \cdot 4\pi r^2 \)
The electric flux (Φ) through the Gaussian surface is the product of the electric field (E) and the surface area (A) of the Gaussian surface:
\(\displaystyle \Phi = E \cdot A = E \cdot 4\pi r^2 \)
Gauss’s Law states that the total electric flux through a closed surface is equal to the charge enclosed divided by the permittivity of free space (\(\displaystyle\varepsilon_0 \)):
\(\displaystyle \Phi = \frac{Q}{\varepsilon_0} \)
Equating the two expressions for (Φ) and solving for (E) gives us:
\(\displaystyle E \cdot 4\pi r^2 = \frac{Q}{\varepsilon_0} \)
\(\displaystyle E = \frac{1}{4\pi\varepsilon_0} \frac{Q}{r^2} \)
The electric field (E) at a point outside a uniformly charged thin spherical shell is as if all the charge were concentrated at the center of the shell. It decreases with the square of the distance from the center, similar to the field created by a point charge.
(b) Field Inside The Shell (r < R)
For a point inside the shell, we choose a spherical Gaussian surface with radius (r) such that (r < R). This surface is concentric with the charged shell. The Gaussian surface is inside the shell and the shell has no thickness, there is no charge enclosed by the Gaussian surface. Therefore, (Qenc = 0 ).

The electric flux (Φ) through the Gaussian surface is the product of the electric field (E) and the surface area (A) of the Gaussian surface:
\(\displaystyle \Phi = E \cdot A = E \cdot 4\pi r^2 \)
Gauss’s Law states that the total electric flux through a closed surface is equal to the charge enclosed divided by the permittivity of free space (\(\displaystyle\varepsilon_0 \)):
\(\displaystyle \Phi = \frac{Q_{\text{enc}}}{\varepsilon_0} \)
Since (Qenc = 0 ), the electric flux (Φ) is also zero. Therefore, the electric field (E) inside the shell is:
E = 0
The electric field ( E ) at any point inside a uniformly charged thin spherical shell is zero. This result is quite remarkable because it tells us that no matter how much charge is on the shell if you are inside it, you will not experience any electric field due to that charge.
(c) Field On The Surface Of The Shell (r = R)
For a point on the surface (r = R), we choose a spherical Gaussian surface that coincides with the charged shell itself.
The electric flux (Φ) through the Gaussian surface is the product of the electric field ( E ) and the surface area (A) of the Gaussian surface:
\(\displaystyle \Phi = E \cdot A = E \cdot 4\pi R^2 \)
Gauss’s Law states that the total electric flux through a closed surface is equal to the charge enclosed divided by the permittivity of free space (\(\displaystyle\varepsilon_0 \)):
\(\displaystyle \Phi = \frac{Q}{\varepsilon_0} \)
Equating the two expressions for (Φ) and solving for (E) gives us:
\(\displaystyle E \cdot 4\pi R^2 = \frac{Q}{\varepsilon_0} \)
\(\displaystyle E = \frac{1}{4\pi\varepsilon_0} \frac{Q}{R^2} \)
It shows that the electric field at the surface is directly proportional to the total charge (Q) and inversely proportional to the square of the radius (R) of the shell.
Electric Field due to a Uniformly Charged Sphere
Consider a sphere with a uniform charge density and total charge (Q). We want to find the electric field at a point outside the sphere, at a distance (r) from the center of the sphere.
The field at an Outside Point:
For a sphere, the best Gaussian surface is another sphere (a spherical shell) centered on the charged sphere and with a radius (r) such that (r > R), where (R) is the radius of the charged sphere. Due to the symmetry of a sphere, the electric field (E) at any point on the Gaussian surface is the same and points radially outward from the center.
The electric flux (Φ) through the Gaussian surface is the product of the electric field (E) and the surface area (A) of the Gaussian surface:
\(\displaystyle\Phi = E \cdot A = E \cdot 4\pi r^2 \)
Gauss’s Law states that the total electric flux through a closed surface is equal to the charge enclosed divided by the permittivity of free space (\(\displaystyle\varepsilon_0 )\)):
\(\displaystyle \Phi = \frac{Q}{\varepsilon_0} \)
Equating the two expressions for (Φ) and solving for (E) gives us:
\(\displaystyle E \cdot 4\pi r^2 = \frac{Q}{\varepsilon_0} \)
\(\displaystyle E = \frac{1}{4\pi\varepsilon_0} \frac{Q}{r^2} \)
The expression shows that the electric field decreases with the square of the distance from the center of the sphere, which is similar to the electric field created by a point charge.
The field at an Internal Point:
Consider a sphere with a uniform volume charge density (ρ) and total charge (Q). We want to find the electric field at a point inside the sphere, at a distance (r) from the center of the sphere, where (r < R) and (R) is the radius of the sphere.
For a point inside the sphere, we choose a spherical Gaussian surface concentric with the charged sphere and with radius (r). Due to the symmetry of a sphere, the electric field (E) at any point on the Gaussian surface is the same and points radially outward from the center.
The charge enclosed by the Gaussian surface is a portion of the total charge (Q). It can be found by the ratio of the volumes:
\(\displaystyle Q_{\text{enc}} = \frac{4}{3}\pi r^3 \cdot \rho \)
Electric Flux Through the Gaussian Surface: The electric flux (Φ) through the Gaussian surface is the product of the electric field (E) and the surface area (A) of the Gaussian surface:
\(\displaystyle \Phi = E \cdot A = E \cdot 4\pi r^2 \)
Gauss’s Law states that the total electric flux through a closed surface is equal to the charge enclosed divided by the permittivity of free space (\(\displaystyle\varepsilon_0 \)):
\(\displaystyle \Phi = \frac{Q_{\text{enc}}}{\varepsilon_0} \)
Equating the two expressions for (Φ) and solving for (E) gives us:
\(\displaystyle E \cdot 4\pi r^2 = \frac{\frac{4}{3}\pi r^3 \cdot \rho}{\varepsilon_0} \)
\(\displaystyle E = \frac{\rho \cdot r}{3\varepsilon_0} \)
Since the charge is uniformly distributed, the volume charge density (ρ) is related to the total charge (Q) by:
\(\displaystyle \rho = \frac{Q}{\frac{4}{3}\pi R^3} \)
Substituting (ρ) into our expression for (E) gives us:
\(\displaystyle E = \frac{\frac{Q}{\frac{4}{3}\pi R^3} \cdot r}{3\varepsilon_0} \)
\(\displaystyle E = \frac{Qr}{4\pi\varepsilon_0 R^3} \)
This expression shows that the electric field inside the sphere increases linearly with the distance from the center, up to the surface of the sphere.
Electric Field near a Charged Conducting Surface
Consider a large, flat, charged conducting surface with a uniform surface charge density (σ). We want to find the electric field just outside this surface. For a flat conducting surface, we choose a Gaussian “pillbox” surface that straddles the conducting surface. This pillbox has two flat ends, one inside the conductor and one just outside it, and a curved side surface.
Due to the symmetry of the problem, the electric field (E) just outside the conducting surface is perpendicular to the surface and has the same magnitude everywhere on the outside flat end of the pillbox.
The electric flux (Φ) through the Gaussian surface is only through the flat end just outside the conductor because the electric field inside the conductor is zero. If (A) is the area of the flat end, the total flux (Φ) through the pillbox is (Φ = E ∙ A).
Applying Gauss’s Law: Gauss’s Law states that the total electric flux through a closed surface is equal to the charge enclosed divided by the permittivity of free space (∊0):
\(\displaystyle \Phi = \frac{Q_{\text{enc}}}{\varepsilon_0} \)
The charge enclosed by the pillbox is just the charge on the outside flat end, which is ( Qenc = σ ∙A).
Equating the two expressions for (Φ) and solving for (E) gives us:
\(\displaystyle E \cdot A = \frac{\sigma \cdot A}{\varepsilon_0} \)
\(\displaystyle E = \frac{\sigma}{\varepsilon_0} \)
This expression shows that the electric field just outside the surface is directly proportional to the surface charge density (σ) and does not depend on the distance from the surface.
Also Read: Electric Field Lines
Solved Examples
Problem 1: An infinitely long straight wire has a uniform linear charge density (\(\displaystyle \lambda = 2 \times 10^{-6} \ \text{C/m} \)). Calculate the electric field at a distance (r = 0.1 m) from the wire.
Solution: Using Gauss’s Law, we know that for an infinitely long straight wire, the electric field (E) at a distance (r) from the wire is given by:
\(\displaystyle E = \frac{\lambda}{2 \pi \epsilon_0 r} \)
Given: \(\displaystyle \epsilon_0 = 8.85 \times 10^{-12} \ \text{C}^2/\text{N} \cdot \text{m}^2 \)
Substituting the values:
\(\displaystyle E = \frac{2 \times 10^{-6}}{2 \pi \times 8.85 \times 10^{-12} \times 0.1} \)
Calculating:
\(\displaystyle E = \frac{2 \times 10^{-6}}{5.56 \times 10^{-12}} \)
\(\displaystyle E \approx 3.59 \times 10^{5} \ \text{N/C} \)
Problem 2: A uniformly charged infinite plane sheet has a surface charge density (\(\displaystyle \sigma = 5 \times 10^{-6} \ \text{C/m}^2 \)). Calculate the electric field at a point near the sheet.
Solution: The electric field (E) due to a uniformly charged infinite plane sheet is given by:
\(\displaystyle E = \frac{\sigma}{2 \epsilon_0} \)
Substituting the values:
\(\displaystyle E = \frac{5 \times 10^{-6}}{2 \times 8.85 \times 10^{-12}} \)
Calculating:
\(\displaystyle E = \frac{5 \times 10^{-6}}{1.77 \times 10^{-11}} \)
\(\displaystyle E \approx 2.82 \times 10^{5} \ \text{N/C} \)
Problem 3: A uniformly charged thin spherical shell has a radius (R = 0.2 m) and a total charge (\(\displaystyle Q = 1 \times 10^{-6} \ \text{C} \)). Calculate the electric field at a distance (r = 0.3 m) from the center of the shell.
Solution: For (\(\displaystyle r \geq R \)), the electric field (E) outside a uniformly charged thin spherical shell is given by:
\(\displaystyle E = \frac{Q}{4 \pi \epsilon_0 r^2} \)
Substituting the values:
\(\displaystyle E = \frac{1 \times 10^{-6}}{4 \pi \times 8.85 \times 10^{-12} \times (0.3)^2} \)
Calculating:
\(\displaystyle E = \frac{1 \times 10^{-6}}{3.33 \times 10^{-11}} \)
\(\displaystyle E \approx 3.00 \times 10^{4} \ \text{N/C} \)
Problem 4: A uniformly charged sphere has a radius (R = 0.2 m) and a charge density (\(\displaystyle \rho = 1 \times 10^{-6} \ \text{C/m}^3 \)). Calculate the electric field at a distance (r = 0.1 m) from the center of the sphere.
Solution: For (r < R), the electric field (E) inside a uniformly charged sphere is given by:
\(\displaystyle E = \frac{\rho r}{3 \epsilon_0} \)
Substituting the values:
\(\displaystyle E = \frac{1 \times 10^{-6} \times 0.1}{3 \times 8.85 \times 10^{-12}} \)
Calculating:
\(\displaystyle E = \frac{1 \times 10^{-7}}{2.655 \times 10^{-11}} \)
\(\displaystyle E \approx 3.77 \times 10^{3} \ \text{N/C} \)
Problem 5: A large flat conducting surface has a surface charge density (\(\displaystyle \sigma = 1 \times 10^{-6} \ \text{C/m}^2\) ). Calculate the electric field just outside the surface.
Solution: The electric field (E) just outside a charged conducting surface is given by:
\(\displaystyle E = \frac{\sigma}{\epsilon_0} \)
Substituting the values:
\(\displaystyle E = \frac{1 \times 10^{-6}}{8.85 \times 10^{-12}} \)
Calculating:
\(\displaystyle E = \frac{1 \times 10^{-6}}{8.85 \times 10^{-12}} \)
\(\displaystyle E \approx 1.13 \times 10^{5} \ \text{N/C} \)
Problem 6: A conducting sphere of radius (R = 0.2 m) carries a charge (\(\displaystyle Q = 2 \times 10^{-6} \ \text{C} \)). Estimate the electric field just outside the surface of the sphere.
Solution: The electric field (E) just outside a uniformly charged conducting sphere is given by:
\(\displaystyle E = \frac{Q}{4 \pi \epsilon_0 R^2} \)
Substituting the values:
\(\displaystyle E = \frac{2 \times 10^{-6}}{4 \pi \times 8.85 \times 10^{-12} \times (0.2)^2} \)
\(\displaystyle E = \frac{2 \times 10^{-6}}{8.85 \times 10^{-12} \times 0.04} \)
\(\displaystyle E \approx 1.80 \times 10^{5} \ \text{N/C} \)
FAQs
What is Gauss’s Law?
Gauss’s Law states that the total electric flux through a closed surface is equal to the charge enclosed by the surface divided by the permittivity of the medium. It provides a relationship between the electric field and the distribution of electric charge.
How can Gauss’s Law be applied to calculate the electric field of a point charge?
For a point charge, Gauss’s Law can be applied by considering a spherical surface centered on the charge. The symmetry of the problem allows us to determine that the electric field is radial and uniform on the surface, simplifying the calculation of the field.
What is the significance of symmetry in applying Gauss’s Law?
Symmetry is crucial in applying Gauss’s Law effectively. Problems with spherical, cylindrical, or planar symmetry allow for simpler calculations because the electric field is uniform over the chosen Gaussian surface, making it easier to compute the flux.
How does Gauss’s Law explain the behavior of conductors in electrostatic equilibrium?
Gauss’s Law explains that the electric field inside a conductor in electrostatic equilibrium is zero. Any excess charge resides on the surface of the conductor, creating a field outside but none inside. This is because the charges distribute themselves to cancel the internal field.
What is a Gaussian surface and how is it chosen?
A Gaussian surface is an imaginary closed surface used in applying Gauss’s Law. It is chosen based on the symmetry of the problem to simplify calculations. Common shapes include spheres, cylinders, and planes that match the symmetry of the charge distribution.
What is a corollary of the Gauss Theorem?
A corollary of the Gauss Theorem is that the net electric flux through any closed surface surrounding a charge distribution is independent of the shape or size of the surface. It only depends on the total charge enclosed within the surface.
How does Gauss’s Law apply to an infinite plane of charge?
For an infinite plane of charge, Gauss’s Law is applied using a cylindrical Gaussian surface perpendicular to the plane. Due to symmetry, the electric field is uniform and perpendicular to the plane, allowing the flux to be easily calculated and showing that the field is constant and independent of distance from the plane.