The story of gravitational potential begins with the ancient Greeks. They were the first to start thinking deeply about the forces that govern the movement of objects. Aristotle, for example, believed that objects fell towards the Earth due to their nature. Fast forward to the Middle Ages and the Renaissance, scholars across the world, including Indian astronomer Brahmagupta, began to describe gravity as an attractive force. This period also saw the development of the theory of impetus, which was an early step towards understanding momentum and energy.
The real game-changer came during the Scientific Revolution with Sir Isaac Newton. He formulated the Universal Law of Gravitation, which described the force of gravity between two masses. Newton’s law was revolutionary because it was universal; it applied to the apple falling from the tree and the planets orbiting the Sun.
The concept of gravitational potential itself was introduced later. It was first noted by Daniel Bernoulli in the 18th century, who observed that in fluid motion, forces could be derived from the differentiation of a scalar function. This idea was then applied to gravitational fields by great mathematicians like Euler, Lagrange, Laplace, and Legendre.
Newton’s ideas set the stage for over two centuries of physics, but they were eventually superseded by Albert Einstein’s theory of relativity in the early 20th century. However, the concept of gravitational potential remains a fundamental part of classical mechanics, especially when dealing with forces and energy in a gravitational field.
Potential at a Point
The potential at a point in a field is the work done in bringing a unit mass from infinity to that point, without any acceleration. Imagine you’re at a water park, and you have a ball that you want to take to the top of a water slide. The effort you put into carrying the ball up against gravity is similar to the work done in moving a mass in a gravitational field.
The source field is like the layout of the water park. It’s the environment that creates the conditions for potential. In physics, this could be a gravitational field around a planet or an electric field around a charged object.
When you move the ball from point A (the bottom of the slide) to point B (the top), you’re working against the gravitational pull. Similarly, moving a test mass (m) from point A to B in a source field (\(\displaystyle \vec{X} \)) involves work, but without changing the ball’s speed (kinetic energy).
The potential difference between points A and B, denoted as (\(\displaystyle V_B – V_A \)), is the work done per unit mass to move from A to B:
\(\displaystyle V_B – V_A = \frac{W_{A \to B}}{m} \)
Unlike the height of the water slide, the potential at a point isn’t absolute. We can’t measure it directly. We measure the difference in potential, like measuring the height difference between two points on the slide. We choose a reference point where we assume the potential is zero, like considering the ground level as zero height. In physics, we often take this reference point at infinity, where the influence of the source field is negligible.
If we take point A at infinity, where (VA = 0 ), then the potential at point B becomes:
\(\displaystyle V_B = \frac{W_{\infty \to B}}{m} \)
This equation tells us how much work is needed to bring a unit mass from far away (infinity) to point B in the source field. Think of the potential at point B as the “height” of the water slide. It represents how much work you need to do to bring the ball to that point. Just as it takes more effort to carry the ball higher, it takes more work to move a mass against a stronger gravitational or electric field.
What is Gravitational Potential
Gravitational Potential (V) at a point is the amount of work done per unit mass to bring a small test mass from infinity to that point. It’s measured in Joules per kilogram (J/kg). Imagine you’re on a mountain with a ball in your hand. If you let go of the ball, it will fall to the ground. Now, before you release it, the ball has the potential to do something—in this case, fall. This is similar to gravitational potential, which is essentially the potential energy per unit mass at a point in a gravitational field due to its position.
A gravitational field is like an invisible force field around a massive object, like Earth, that pulls other objects towards its center. The further you are from the object, the weaker the pull. Now, potential energy is the stored energy of position possessed by an object. In the case of the ball, the higher up the mountain you are, the more potential energy it has.
Gravitational potential at a point in the field is defined as the work done (energy transferred) in bringing a unit mass from infinity to that point, without any acceleration. It’s like how much effort you would need to bring the ball from space (infinity) to the mountaintop without speeding it up or slowing it down.
The formula for gravitational potential (V) at a distance (r) from a mass (M) is:
\(\displaystyle V = -\frac{GM}{r} \)
where (G) is the gravitational constant, and (r) is the distance from the center of the mass to the point in question. Notice the negative sign in the formula. It indicates that the gravitational potential is always negative, which means you need to do work to bring a mass from infinity to a point in the gravitational field, against the pull of gravity.
We say “per unit mass” because gravitational potential is independent of the mass of the object being moved. Whether it’s a tennis ball or a boulder, the gravitational potential at a particular point on the mountain is the same. Gravitational potential is a measure of the potential energy that a unit mass would have at a point in a gravitational field. It’s a way of quantifying the “potential” for work to be done by gravity on an object at a specific location.
Gravitational Potential due to a Point Mass
Gravitational potential due to a point mass is a way to quantify the “energy currency” a unit mass has in a gravitational field created by the point mass. It’s a fundamental concept that helps us understand how objects will move in space due to gravity’s influence. Imagine you’re in space, far away from any planets or stars. You have a single-point mass, like a small moon. This point mass creates a gravitational field around it, pulling things towards itself.
Gravitational potential at a point in this field is a measure of the potential energy that a unit mass would have due to its position relative to the point mass. It’s like having a certain amount of “energy currency” based on where you are in space. To understand the gravitational potential, think about the work you’d need to do to bring a unit mass (say, 1 kg) from a place very far away (infinity) to a specific point near the point mass. This work is done against the gravitational pull of the point mass.
The formula for calculating the gravitational potential (V) due to a point mass (M) at a distance (r) is:
\(\displaystyle V = -\frac{GM}{r} \)
where (G) is the gravitational constant. The negative sign indicates that you’re moving against the gravitational pull, which is an attractive force. As you get closer to the point mass, you’re going into a deeper “gravitational well,” and the potential becomes more negative.
This potential doesn’t depend on the mass of the object you’re moving. Whether it’s a feather or a lead ball, the gravitational potential at that point in space is the same. Think of gravitational potential as the depth of a well. The point mass is at the bottom, and the further you are from the bottom, the less “deep” you are in the well. Bringing a unit mass closer to the point mass is like lowering it deeper into the well.
Deriving Gravitational Potential due to a Point Mass
Gravitational potential at a point is the work done per unit mass to bring an object from infinity to that point in a gravitational field. It’s like the energy “credit” you get for moving closer to a massive object in space. Consider a point mass (M) in space. We want to find out the gravitational potential at a distance (r) from this mass.
To calculate the potential, we need to find the work done in bringing a unit mass from infinity to a distance (r) from the point mass. Since gravitational force is conservative, the work done is independent of the path taken. The gravitational force (F) exerted by the point mass (M) on a unit mass at a distance (r) is given by Newton’s law of gravitation:
\(\displaystyle F = \frac{GM}{r^2} \)
The work (dW) done in moving the unit mass an infinitesimal distance (dr) towards the point mass is:
\(\displaystyle dW = F \cdot dr = \frac{GM}{r^2} \cdot dr \)
To find the total work done in bringing the unit mass from infinity to a distance (r), we integrate (dW) from (r) to infinity:
\(\displaystyle W = \int_{\infty}^{r} \frac{GM}{r^2} \cdot dr \)
Performing the integration, we get:
\(\displaystyle W = -GM \left[ \frac{1}{r} \right]_{\infty}^{r} \)
\(\displaystyle W = -GM \left( \frac{1}{r} – \frac{1}{\infty} \right) \)
Since (\(\displaystyle \frac{1}{\infty} \)) is zero, we simplify to:
\(\displaystyle W = -\frac{GM}{r} \)
The gravitational potential (V) is the work done per unit mass, so we have:
\(\displaystyle V = \frac{W}{m} \)
But since we’ve considered a unit mass, (m = 1), the expression for gravitational potential (V) due to a point mass (M) at a distance (r) is:
\(\displaystyle V = -\frac{GM}{r} \)
The negative sign indicates that the gravitational potential is always negative, reflecting the fact that work must be done against the gravitational pull to bring the mass from infinity to the point. The derived expression (\(\displaystyle V = -\frac{GM}{r} \)) tells us the gravitational potential due to a point mass at a certain distance. It’s a crucial concept in understanding the gravitational interactions between objects in space.
Relation between Gravitational Potential and Gravitational Field
First, let’s talk about the gravitational field. Imagine you’re near a planet, and you throw a ball straight up. The ball will slow down, stop, and then fall back down. The planet’s gravitational field is what pulls the ball back. It’s a vector field that describes the gravitational force felt by a small test mass at various points in space.
Now, gravitational potential is a bit different. It’s not about force but about potential energy per unit mass. If you lift the ball higher, you’re increasing its gravitational potential because it has more “potential” to do work if it falls.
The relationship between gravitational potential (V) and the gravitational field (\(\displaystyle \vec{E} \)) is quite elegant. The gravitational field is the gradient of the gravitational potential. In simpler terms, if you look at how the gravitational potential changes from one point to another, you’re looking at the gravitational field.
Mathematically, the gravitational field ( \(\displaystyle\vec{E} \)) at a point is the negative gradient (rate of change) of the gravitational potential (V) at that point:
\(\displaystyle \vec{E} = -\nabla V \)
This equation tells us that the gravitational field points in the direction where the gravitational potential decreases the fastest. Think of a hill with contour lines on a map. Each line represents a constant potential. The gravitational field is like the slope of a hill. The steeper the slope, the stronger the gravitational field. And just like water flows down the steepest path, a mass moves in the direction of the strongest gravitational pull.
This relationship is crucial because it allows us to calculate the force on an object just by knowing the potential at different points. For example, if we know the gravitational potential around Earth, we can predict the path of a satellite or the trajectory of a comet. The gravitational potential gives us a “landscape” of potential energy values, while the gravitational field tells us how objects will move within that landscape.
Gravitational potential (V) at a distance (r) from a mass (M) is given by:
\(\displaystyle V = -\frac{GM}{r} \)
The gravitational field (\(\displaystyle \vec{E} \)) is defined as the force per unit mass at a point in space due to a mass (M). It can be calculated by the formula:
\(\displaystyle \vec{E} = -\frac{GM}{r^2} \hat{r} \)
To find the relationship between (V) and (\(\displaystyle \vec{E} \)), we take the gradient of (V). The gradient of a scalar field gives us a vector field that points in the direction of the greatest rate of increase of the scalar field.
The gradient in spherical coordinates for a radially symmetric field like gravity is:
\(\displaystyle \nabla V = \frac{dV}{dr} \hat{r} \)
Differentiating (V) with respect to (r), we get:
\(\displaystyle \frac{dV}{dr} = \frac{d}{dr} \left( -\frac{GM}{r} \right) = \frac{GM}{r^2} \)
Since the gravitational field is the negative gradient of the potential, we apply a negative sign to the derivative we just found:
\(\displaystyle \vec{E} = -\nabla V = -\frac{dV}{dr} \hat{r} = -\frac{GM}{r^2} \hat{r} \)
This gives us the final expression that relates gravitational potential and gravitational field:
\(\displaystyle \vec{E} = -\nabla V \)
This derivation shows that the gravitational field at any point is simply the negative gradient of the gravitational potential at that point. It’s a beautiful and simple relationship that tells us how the potential energy landscape translates into forces that act on masses.
How does gravitational potential relate to escape velocity?
The escape velocity is directly related to the gravitational potential energy. An object must have enough kinetic energy to counteract its gravitational potential energy to escape the gravitational field. Gravitational potential and escape velocity are closely related to the concept of energy conservation in gravitational fields.
Gravitational potential energy (U) at a distance (r) from a mass (M) is given by:
\(\displaystyle U = -\frac{GMm}{r} \)
where (G) is the gravitational constant, (M) is the mass of the body creating the gravitational field, (m) is the mass of the object, and (r) is the distance from the center of (M) to the object.
Escape velocity is the minimum velocity an object must have to overcome the gravitational pull of a celestial body and escape into space without further propulsion. It’s like hitting the perfect speed on a swing that allows you to fly off into the sky instead of coming back down.
To derive the escape velocity, we use the principle of conservation of energy. The total mechanical energy (kinetic plus potential) of an object must be zero to escape the gravitational influence of a celestial body:
\(\displaystyle \frac{1}{2}mv_{escape}^2 – \frac{GMm}{r} = 0 \)
Solving for (\(\displaystyle v_{escape} \)), we get:
\(\displaystyle \frac{1}{2}mv_{escape}^2 = \frac{GMm}{r} \)
\(\displaystyle v_{escape}^2 = \frac{2GM}{r} \)
\(\displaystyle v_{escape} = \sqrt{\frac{2GM}{r}} \)
This derivation shows that the escape velocity depends on the gravitational potential at the point of escape. The deeper the gravitational potential well (the larger the (M) and the smaller the (r), the higher the escape velocity needed. This is why rockets need so much speed (and fuel) to leave Earth—they need to reach escape velocity to break free from Earth’s gravitational potential.
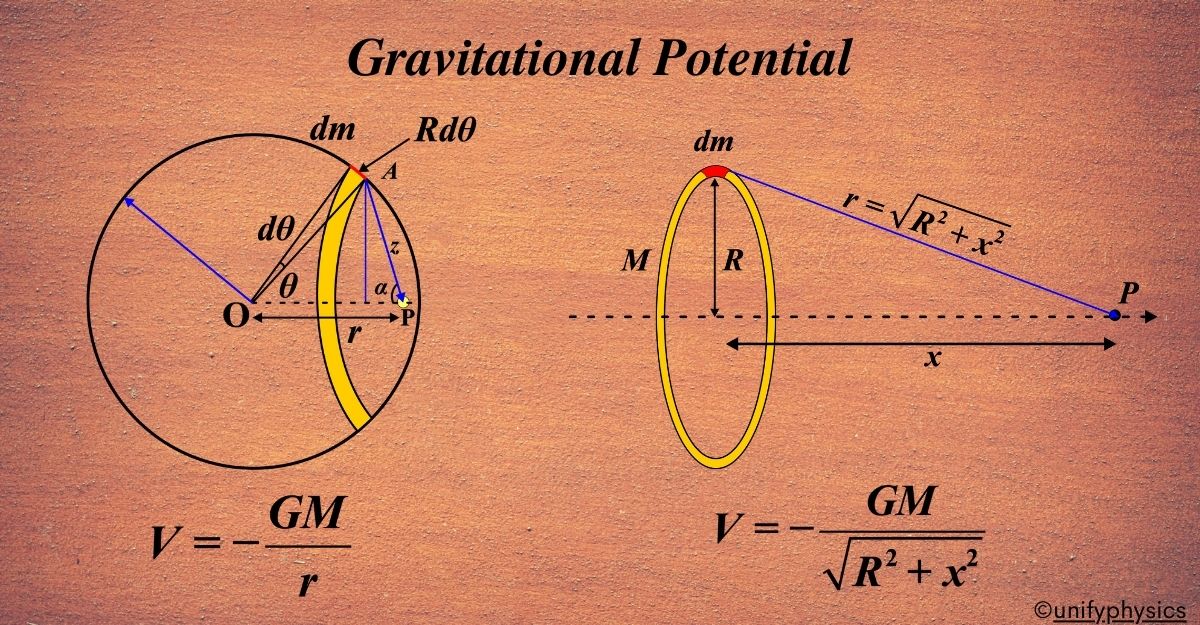
Gravitational Potential due to Uniform Ring on its Axial Point
The gravitational potential due to a uniform ring on its axial point is a way to understand the “energy landscape” created by the ring’s mass. It tells us how much work is needed to move a unit mass to a point along the axis from very far away. Imagine a ring, like a hula hoop, suspended in space. This ring has mass and creates a gravitational field around it. Now, think of an axis that goes through the center of the ring and is perpendicular to its plane. We’re interested in discovering the gravitational potential at various points along this axis.
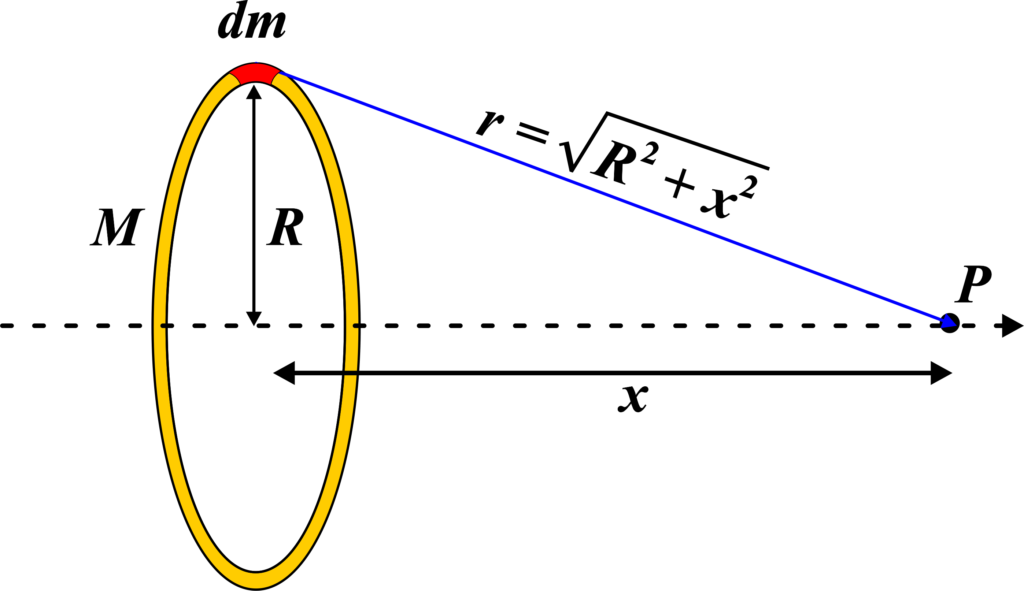
Gravitational potential at a point is the work done in bringing a unit mass from infinity to that point without any acceleration. For our ring, we want to know this potential along the axis we just imagined. To calculate the gravitational potential at a point on the axis, we consider each small part of the ring as a point mass. Each part contributes to the total potential at the point we’re considering.
The gravitational potential (V) at a point on the axis of a uniform ring of mass (M) and radius (R) at a distance (x) from the center of the ring is given by the formula:
\(\displaystyle V = -\frac{GM}{\sqrt{x^2 + R^2}} \)
Think of the gravitational potential as a measure of how much “effort” it would take to bring a small object from far away to that point. The farther you are from the ring, the less effort it takes, which means the potential is less negative. The potential is negative because gravity is an attractive force, and work must be done against it to bring the unit mass from infinity to the point in question.
We want to find the gravitational potential at a point (P) located on the axis of the ring, a distance (x) from the center of the ring. The gravitational potential at a point is the work done to bring a unit mass from infinity to that point. For a ring, we need to consider the contribution of each infinitesimal mass element (dM) of the ring to the potential at point (P).
The potential (dV) due to an infinitesimal mass element (dM) at point (P) is given by:
\(\displaystyle dV = -\frac{GdM}{r} \)
where (r) is the distance from the element to point (P), and (G) is the gravitational constant.
The distance (r) can be found using the Pythagorean theorem, where (\(\displaystyle r = \sqrt{x^2 + R^2} \)), since (x) and (R) are perpendicular to each other.
To find the total potential (V) at point (P), we integrate (dV) over the entire ring:
\(\displaystyle V = \int dV = -\int \frac{GdM}{\sqrt{x^2 + R^2}} \)
Since ( \(\displaystyle\sqrt{x^2 + R^2} \)) is constant for all elements of the ring and (G) is a constant, we can take them outside the integral:
\(\displaystyle V = -\frac{G}{\sqrt{x^2 + R^2}} \int dM \)
The integral (\(\displaystyle \int dM \)) is simply the total mass of the ring, (M). Putting it all together, we get the expression for the gravitational potential (V) at point (P) on the axis of the ring:
\(\displaystyle V = -\frac{GM}{\sqrt{x^2 + R^2}} \)
The negative sign indicates that the gravitational potential is always negative, reflecting the fact that work must be done against the gravitational pull to bring the mass from infinity to the point.
The derived expression (\(\displaystyle V = -\frac{GM}{\sqrt{x^2 + R^2}} \)) tells us the gravitational potential due to a uniform ring at a point on its axis. Now the gravitational field along the axis of the ring can be written as,
Imagine a uniform ring of mass (M) and radius (R). We want to find the gravitational field at a point (P) located on the axis of the ring, a distance (x) from the center of the ring. The gravitational field at a point is the gravitational force experienced by a unit mass at that point. For our ring, we need to consider the contribution of each infinitesimal mass element (dM) of the ring to the field at point (P).
The field (\(\displaystyle d\vec{E}\)) due to an infinitesimal mass element (dM) at point (P) is given by:
\(\displaystyle d\vec{E} = \frac{GdM}{r^2} \hat{r} \)
where \(\displaystyle\hat{r} \) is the unit vector from (dM) to (P).
The distance (r) can be found using the Pythagorean theorem, where (\(\displaystyle r = \sqrt{x^2 + R^2} \)), since (x) and (R) are perpendicular to each other.
The elemental field (\(\displaystyle d\vec{E} \)) has two components: one along the axis of the ring and one perpendicular to it. By symmetry, the perpendicular components cancel out, and only the axial component contributes to the net field.
The axial component of (\(\displaystyle d\vec{E} \)) is:
\(\displaystyle dE_{axial} = \frac{GdM}{r^2} \cos{\theta} \)
where (\(\displaystyle \cos{\theta} = \frac{x}{r} \)). To find the total field (E) at point (P), we integrate (\(\displaystyle dE_{axial} \)) over the entire ring:
\(\displaystyle E = \int dE_{axial} = \int \frac{GdM}{(\sqrt{x^2 + R^2})^2} \cdot \frac{x}{\sqrt{x^2 + R^2}} \)
Since (x) and (R) are constants for all elements of the ring, we can simplify the integral:
\(\displaystyle E = \frac{Gx}{(\sqrt{x^2 + R^2})^3} \int dM \)
The integral ( \(\displaystyle\int dM \)) is simply the total mass of the ring, (M). Putting it all together, we get the expression for the gravitational field (E) at point (P) on the axis of the ring:
\(\displaystyle E = \frac{GMx}{(\sqrt{x^2 + R^2})^3} \)
The gravitational field (E) is directed towards the center of the ring, indicating that the gravitational force at point ( P ) would pull a mass towards the ring’s center. The derived expression (\(\displaystyle E = \frac{GMx}{(\sqrt{x^2 + R^2})^3} \)) tells us the magnitude of the gravitational field due to a uniform ring at a point on its axis.
Gravitational Potential due to Uniform Thin Spherical Shell
Consider an elemental ring on the spherical shell with a mass (dm) and an angular thickness (\(\displaystyle d\theta \)). The radius of this ring is (\(\displaystyle R\sin\theta \)), where (R) is the radius of the spherical shell and (\(\displaystyle \theta \)) is the angle from the axis passing through the center.
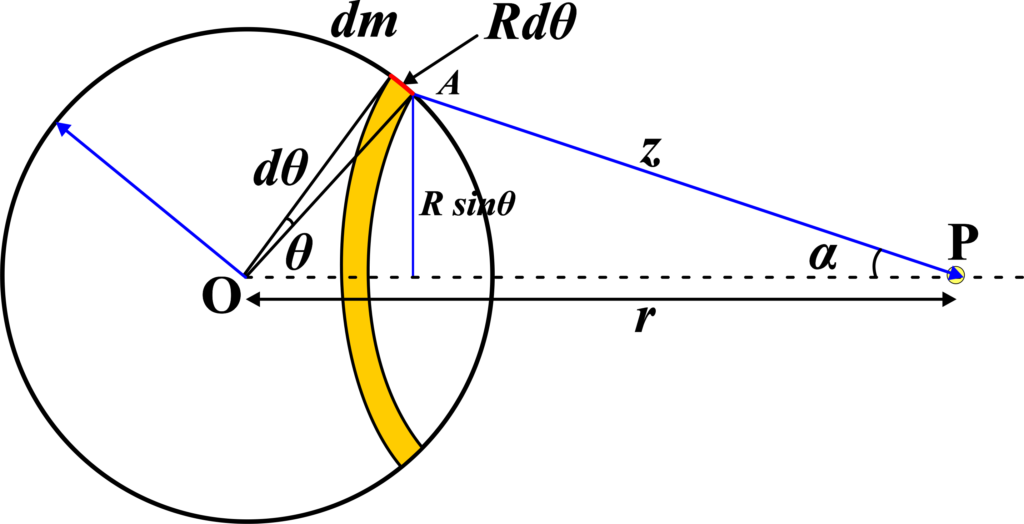
The surface area of the elemental ring is (\(\displaystyle dA = 2\pi R\sin\theta R d\theta \)). The surface mass density (\(\displaystyle \sigma \)) of the shell is (\(\displaystyle \frac{M}{4\pi R^2}\)), where (M) is the total mass of the shell. Therefore, the mass of the elemental ring is:
\(\displaystyle dm = \sigma dA = \frac{M}{4\pi R^2} \cdot 2\pi R\sin\theta R d\theta \) ……….(1)
Simplifying, we get:
\(\displaystyle dm = \frac{M}{2} \sin\theta d\theta \) …………..(2)
In the triangle formed by the center of the shell, the point (P), and a point on the ring, we apply the cosine law:
\(\displaystyle R^2 + r^2 – z^2 = 2Rr\cos\theta \)
Differentiating with respect to (z), we obtain:
\(\displaystyle -2z dz = 2Rr (-\sin\theta d\theta) \)
This gives us:
\(\displaystyle \sin\theta d\theta = \frac{z}{Rr} dz \) ………….(3)
Using the expression for (dm) from eq. (2) and the result from eq. (3), we have:
\(\displaystyle dm = \frac{M}{2} \frac{z}{Rr} dz \) ………….(4)
The gravitational potential contribution (dV) from the elemental mass (dm) at point (P) is:
\(\displaystyle dV = -\frac{Gdm}{z} \)
Substituting (dm) from eq. (4), we get:
\(\displaystyle dV = -\frac{GM}{2} \frac{z}{Rr} \frac{dz}{z} \)
Simplifying, we have:
\(\displaystyle dV = -\frac{GM}{2Rr} dz \)
Therefore the potential at point P due to the spherical shell is,
\(\displaystyle V=\int{{dV}}=-\int{{\frac{{GM}}{{2Rr}}}}dz\) ……….(5)
(i) Case 1: If the point (P) is outside the shell (r > R)
The potential is the same as if the entire mass (M) were concentrated at the center. If the point P is present outside the shell while integrating the equation (5), then limits for z will be (r-R) at point 1 and (r+R) at point 2. Then from equation (5),
\(\displaystyle V=-\int\limits_{{r-R}}^{{r+R}}{{\frac{{GM}}{{2Rr}}}}dz\)
\(\displaystyle V=-\frac{{GM}}{{2Rr}}Z_{{r-R}}^{{r+R}}\)
\(\displaystyle V=-\frac{{GM}}{r}\)
This is derived from the fact that for gravitational effects, the mass of a spherical shell can be considered to be concentrated at its center when calculating the potential at points outside the shell.
(ii) Case 2: If the point (P) is inside the shell (r < R)
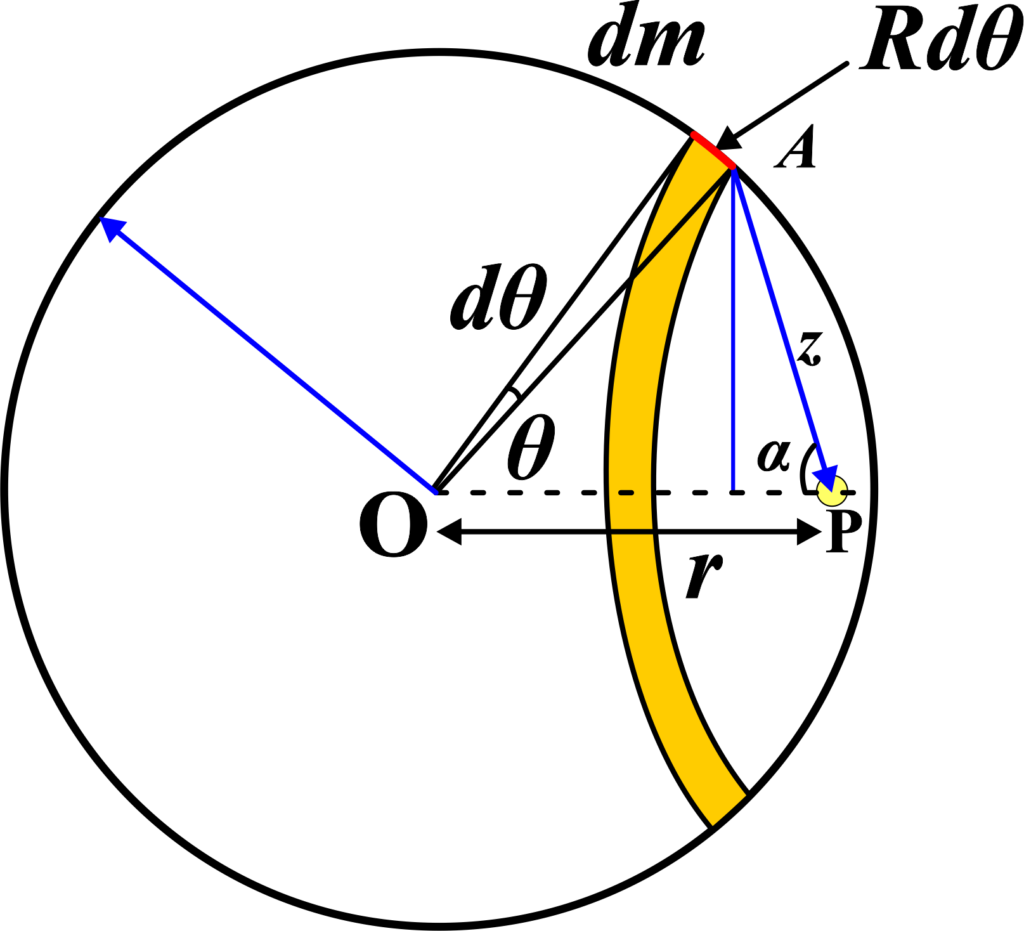
The potential is constant and equal to the value on the surface. If the point P is present inside the shell then while integrating equation (5), the limits for z will be (R-r) at point 1 and (R+r) at point 2. Then from again equation (5),
\(\displaystyle V=-\int\limits_{{R-r}}^{{R+r}}{{\frac{{GM}}{{2Rr}}}}dz\)
\(\displaystyle V=-\frac{{GM}}{{2Rr}}Z_{{R-r}}^{{R+r}}\)
\(\displaystyle V=-\frac{{GM}}{R}\)
This is because, according to the shell theorem, there is no net gravitational force experienced by a particle inside a uniform spherical shell, and thus the potential remains the same as on the surface.
Gravitational Potential Due to Uniform Solid Sphere
A uniform solid sphere can be considered a composition of an infinite number of uniform spherical shells. Consider a uniform solid sphere of mass M and radius R and let the sphere be made up of many shells, each of mass dm. Then the total mass of the solid sphere will be written as, \(\displaystyle M=\sum{{dm}}\)

The gravitational potential becomes
\(\displaystyle dV=-\frac{{Gdm}}{r}\)
Let a point P on the line passing through the center of the solid sphere at which we have to find the gravitational potential.
Case 1: Point (P) Outside the Sphere (r > R)
To derive the expression for the gravitational potential due to a uniform solid sphere for a point outside the sphere (r > R), where (R) is the radius of the sphere, we’ll use the concept of superposition of gravitational potential from different mass elements of the sphere.
Imagine a solid sphere with radius (R) and total mass (M). The sphere’s mass is uniformly distributed throughout its volume.
The gravitational potential (dV) at a point (P) due to a small mass element (dm) inside the sphere is given by:
\(\displaystyle dV = -\frac{Gdm}{r’} \)
(r’) is the distance from the mass element to point (P). The total gravitational potential (V) at point (P) is the sum (integral) of the potentials due to all such mass elements (dm) within the sphere.
According to the shell theorem, the gravitational potential outside a uniform sphere is the same as if all its mass were concentrated at its center. Therefore, the potential at point (P) is the same as if the entire mass (M) of the sphere were located at a point at its center.
The gravitational potential (V) at point (P) outside the sphere is given by the formula for the potential due to a point mass:
\(\displaystyle V = -\frac{GM}{r} \)
where (r) is the distance from the center of the sphere to point (P).
The negative sign indicates that the potential is negative, which is characteristic of attractive forces like gravity. The potential decreases with increasing distance from the sphere, which aligns with the inverse-square law of gravitation.
For a point (P) outside a uniform solid sphere (r > R), the gravitational potential is given by (\(\displaystyle V = -\frac{GM}{r} \)). This formula is derived based on the assumption that the mass of the sphere acts as if it were concentrated at its center.
Case 2: Point (P) Inside the Sphere (r < R)
For a point inside the sphere, we need to consider the mass of the sphere that lies within a radius (r) from the center. We can think of the sphere as being composed of many thin shells, each contributing to the potential at point (P).
The density (ρ) of the sphere is constant and given by:
\(\displaystyle \rho = \frac{M}{\frac{4}{3}\pi R^3} \)
Consider an elemental shell at a distance (r’) from the center with a thickness (dr’). The mass (dm) of this shell is:
\(\displaystyle dm = 4\pi r’^2 \rho dr’ \)
The gravitational potential (dV) at point (P) due to this elemental shell is:
\(\displaystyle dV = -\frac{Gdm}{r’} \)
To find the total gravitational potential (V) at point (P), we integrate (dV) from (0) to (r):
\(\displaystyle V = \int_{0}^{r} -\frac{G \cdot 4\pi r’^2 \rho dr’}{r’} \)
Simplifying, we get:
\(\displaystyle V = -\frac{G \cdot 4\pi \rho}{r} \int_{0}^{r} r’^2 dr’ \)
Performing the integration, we have:
\(\displaystyle V = -\frac{G \cdot 4\pi \rho}{r} \left[ \frac{r’^3}{3} \right]_{0}^{r} \)
\(\displaystyle V = -\frac{G \cdot 4\pi \rho}{r} \cdot \frac{r^3}{3} \)
Substituting the value of (ρ), we get:
\(\displaystyle V = -\frac{GM}{2R^3}(3R^2 – r^2) \)
So, the gravitational potential (V) at a point (P) inside a uniform solid sphere is given by:
\(\displaystyle V = -\frac{GM}{2R^3}(3R^2 – r^2) \)
This expression shows that the potential inside the sphere increases quadratically with the distance from the center, which is a result of the increasing mass affecting point (P) as we move outwards from the center.
Gravitational Potential due to Uniform Circular Disc at a Point on its Axis
To derive the expression for the gravitational potential due to a uniform circular disc at a point on its axis, we’ll consider a disc of radius (R) and mass (M), and a point (P) located at a distance (z) from the center of the disc along its axis. We’ll break down the process into steps that are easy to understand.
First, we imagine the disc as being composed of many infinitesimally thin concentric rings. We consider an elemental ring with a small mass (dm) and radius (r), located at a distance (z) from point (P).
The mass (dm) of the elemental ring is a fraction of the total mass (M) of the disc. If (σ) is the surface mass density of the disc (\(\displaystyle\sigma = \frac{M}{\pi R^2} \)), then the mass of the elemental ring is:
\(\displaystyle dm = \sigma \cdot 2\pi r dr \)
The gravitational potential (dV) at point (P) due to the elemental ring is given by:
\(\displaystyle dV = -\frac{Gdm}{\sqrt{r^2 + z^2}} \)
To find the total gravitational potential (V) at point (P), we integrate (dV) over all the rings from (r = 0) to (r = R):
\(\displaystyle V = \int_{0}^{R} -\frac{G \cdot \sigma \cdot 2\pi r dr}{\sqrt{r^2 + z^2}} \)
Performing the integration, we substitute (σ) and simplify to get the expression for (V):
\(\displaystyle V = -2\pi G\sigma \int_{0}^{R} \frac{r dr}{\sqrt{r^2 + z^2}} \)
Let (\(\displaystyle u = r^2 + z^2 \)), then (\(\displaystyle du = 2r dr \)). The limits of integration change accordingly, and we integrate with respect to (u):
\(\displaystyle V = -\pi G\sigma \int_{z^2}^{R^2 + z^2} \frac{du}{\sqrt{u}} \)
\(\displaystyle V = -\pi G\sigma \left[ 2\sqrt{u} \right]_{z^2}^{R^2 + z^2} \)
\(\displaystyle V = -\pi G\sigma \left( 2\sqrt{R^2 + z^2} – 2|z| \right) \)
Since (z) is the distance along the axis, (|z| = z ), we can write:
\(\displaystyle V = -2\pi G\sigma \left( \sqrt{R^2 + z^2} – z \right) \)
Finally, we substitute ( \sigma) back into the equation:
\(\displaystyle V = -\frac{GM}{R^2} \left( \sqrt{R^2 + z^2} – z \right) \)
The gravitational potential (V) due to a uniform circular disc at a point on its axis is given by:
\(\displaystyle V = -\frac{GM}{R^2} \left( \sqrt{R^2 + z^2} – z \right) \)
This expression shows how the potential varies with the distance (z) from the disc along its axis. It’s important for understanding the gravitational effects of disc-shaped objects, such as galaxies or accretion discs around black holes.
If we are asked to find the potential due to an annular disc of inner radius R1 and outer radius R2, then we shall be integrating equation (\(\displaystyle dV = -\frac{Gdm}{\sqrt{r^2 + z^2}} \)), within the new limits.
To find the gravitational potential due to an annular disc with an inner radius (R1) and an outer radius (R2) at a point on its axis, we indeed need to integrate within the new limits (R1) and (R2).
\(\displaystyle V = \int_{R_{1}}^{R_{2}} -\frac{G \cdot \sigma \cdot 2\pi r dr}{\sqrt{r^2 + z^2}} \)
(σ) is the surface mass density of the disc,
(r) is the radial distance from the center of the disc to the elemental ring of mass,
(z) is the distance from the point on the axis to the plane of the disc.
The surface mass density (σ) can be expressed as the total mass (M) of the annular disc divided by its area ( \(\displaystyle\pi (R_2^2 – R_1^2) \)):
\(\displaystyle \sigma = \frac{M}{\pi (R_2^2 – R_1^2)} \)
Substituting (σ) into the integral, we get:
\(\displaystyle V = -\int_{R_{1}}^{R_{2}} \frac{G \cdot \frac{M}{\pi(R_2^2 – R_1^2)} \cdot 2\pi r dr}{\sqrt{r^2 + z^2}} \)
Simplifying, we get:
\(\displaystyle V = -\frac{2GM}{R_2^2 – R_1^2} \int_{R_{1}}^{R_{2}} \frac{r dr}{\sqrt{r^2 + z^2}} \)
To solve the integral, we can use a substitution. Let:
\(\displaystyle u = r^2 + z^2 \)
Then: \(\displaystyle du = 2r dr \). The limits of integration in terms of (u) will be from (\(\displaystyle R_1^2 + z^2 \)) to (\(\displaystyle R_2^2 + z^2 \)).
The integral in terms of (u) is:
\(\displaystyle V = -\frac{GM}{R_2^2 – R_1^2} \int_{R_1^2 + z^2}^{R_2^2 + z^2} \frac{du}{2\sqrt{u}} \)
Simplifying, we have:
\(\displaystyle V = -\frac{GM}{R_2^2 – R_1^2} \left[ \sqrt{u} \right]_{R_1^2 + z^2}^{R_2^2 + z^2} \)
Evaluating the integral, we get:
\(\displaystyle V = -\frac{GM}{R_2^2 – R_1^2} \left( \sqrt{R_2^2 + z^2} – \sqrt{R_1^2 + z^2} \right) \)
This is the expression for the gravitational potential due to an annular disc with inner radius (R1) and outer radius (R2) at a point on its axis a distance (z) away from the center of the disc. The negative sign indicates that the potential is negative, which is characteristic of attractive forces like gravity. The potential decreases with increasing distance from the disc, which aligns with the inverse-square law of gravitation.
Gravitational potential is a fundamental concept in the study of gravity, offering a unique perspective on how mass influences the space around it. In physics, gravitational potential is a scalar field that represents the amount of gravitational potential energy per unit mass at a specific point in space. The gravitational potential at a point in space is a measure of the work that gravity would do in bringing a mass from an infinite distance to that point, per unit mass. As one moves closer to a massive object, the gravitational potential increases, signifying a higher potential energy for an object placed in that field.
Also Read: Gravity
Solved Examples
Problem 1: Calculate the gravitational potential at a distance of (10m) from a point mass of (5 kg).
Solution: The gravitational potential (V) at a distance (r) from a point mass (M) is given by:
\(\displaystyle V = -G \frac{M}{r}\)
Given: \(\displaystyle G = 6.674 \times 10^{-11} \, \text{N m}^2 \text{kg}^{-2} \));
M = 5 kg; r = 10 m
Calculate (V):
\(\displaystyle V = -6.674 \times 10^{-11} \frac{5}{10} \)
\(\displaystyle V = -6.674 \times 10^{-11} \times 0.5 \)
\(\displaystyle V = -3.337 \times 10^{-11} \, \text{J/kg} \)
Therefore, the gravitational potential at a distance of (10 m) from a (5 kg) mass is (\(\displaystyle -3.337 \times 10^{-11} \, \text{J/kg} \)).
Problem 2: Given the gravitational potential (\(\displaystyle V = -\frac{GM}{r} \)), find the gravitational field (E) at a distance (r) from a mass (M).
Solution: The gravitational field (E) is the negative gradient of the gravitational potential (V):
\(\displaystyle E = -\frac{dV}{dr} \)
Given: \(\displaystyle V = -\frac{GM}{r} \);
Calculate ( \(\displaystyle\frac{dV}{dr}\)):
\(\displaystyle \frac{dV}{dr} = \frac{GM}{r^2} \)
Therefore, the gravitational field (E) is:
\(\displaystyle E = -\frac{GM}{r^2} \)
This matches the known formula for the gravitational field due to a point mass, confirming the relationship between gravitational potential and gravitational field.
Problem 3: Calculate the gravitational potential at a point (P) on the axis of a uniform ring of mass (M = 2kg) and radius (R = 1 m), where the distance from the center of the ring to point (P) is ( x = 1 m).
Solution: The gravitational potential (V) at a point on the axis of a uniform ring is given by:
\(\displaystyle V = -G \frac{M}{\sqrt{R^2 + x^2}} \)
Given: \(\displaystyle G = 6.674 \times 10^{-11} \, \text{N m}^2 \text{kg}^{-2} \);
M = 2 kg; R = 1 m; x = 1 m
Calculate (V):
\(\displaystyle V = -6.674 \times 10^{-11} \frac{2}{\sqrt{1^2 + 1^2}} \)
\(\displaystyle V = -6.674 \times 10^{-11} \frac{2}{\sqrt{2}} \)
\(\displaystyle V = -6.674 \times 10^{-11} \frac{2}{1.414} \)
\(\displaystyle V = -6.674 \times 10^{-11} \times 1.414 \)
\(\displaystyle V \approx -9.43 \times 10^{-11} \, \text{J/kg} \)
Therefore, the gravitational potential at the point (P) is approximately (\(\displaystyle -9.43 \times 10^{-11} \, \text{J/kg} \)).
Problem 4: Calculate the gravitational potential at a point inside and at a point outside a uniform thin spherical shell of mass (4 kg) and radius ( 3 m).
Solution: Outside the Shell: The potential at a point outside the shell (distance (r > R) is:
\(\displaystyle V_{\text{outside}} = -G \frac{M}{r} \)
Given: \(\displaystyle G = 6.674 \times 10^{-11} \, \text{N m}^2 \text{kg}^{-2} \);
M = 4 kg; r = 5 m
Calculate (\(\displaystyle V_{\text{outside}} \)):
\(\displaystyle V_{\text{outside}} = -6.674 \times 10^{-11} \frac{4}{5} \)
\(\displaystyle V_{\text{outside}} = -6.674 \times 10^{-11} \times 0.8 \)
\(\displaystyle V_{\text{outside}} = -5.3392 \times 10^{-11} \, \text{J/kg} \)
Inside the Shell: The potential at any point inside the shell (distance (r < R) is the same as on the surface:
\(\displaystyle V_{\text{inside}} = -G \frac{M}{R} \)
Given: R = 3 m; Calculate (\(\displaystyle V_{\text{inside}} \)):
\(\displaystyle V_{\text{inside}} = -6.674 \times 10^{-11} \frac{4}{3} \)
\(\displaystyle V_{\text{inside}} = -6.674 \times 10^{-11} \times 1.333 \)
\(\displaystyle V_{\text{inside}} = -8.9 \times 10^{-11} \, \text{J/kg} \)
Therefore, the gravitational potential at a point outside the shell is (\(\displaystyle -5.3392 \times 10^{-11} \, \text{J/kg} \)) and inside the shell is (\(\displaystyle -8.9 \times 10^{-11} \, \text{J/kg} \)).
Problem 5:Calculate the gravitational potential at the surface of a uniform solid sphere of mass ( 6 kg) and radius (2 m).
Solution: The gravitational potential at the surface of a solid sphere is given by:
\(\displaystyle V = -\frac{3}{2} G \frac{M}{R} \)
Given: \(\displaystyle G = 6.674 \times 10^{-11} \, \text{N m}^2 \text{kg}^{-2} \);
M = 6 kg; R = 2 m
Calculate (V):
\(\displaystyle V = -\frac{3}{2} \times 6.674 \times 10^{-11} \frac{6}{2} \)
\(\displaystyle V = -\frac{3}{2} \times 6.674 \times 10^{-11} \times 3 \)
\(\displaystyle V = -3 \times 6.674 \times 10^{-11} \)
\(\displaystyle V = -20.022 \times 10^{-11} \, \text{J/kg} \)
Therefore, the gravitational potential at the surface of the solid sphere is (\(\displaystyle -20.022 \times 10^{-11} \, \text{J/kg} \)).
Problem 6: Calculate the gravitational potential at a point (P) on the axis of a uniform circular disc of mass (M = 3 kg) and radius (R = 2 m), where the distance from the center of the disc to point (P) is (x = 2 m).
Solution: The gravitational potential (V) at a point on the axis of a uniform circular disc is given by:
\(\displaystyle V = -2 \pi G \frac{M}{\sqrt{R^2 + x^2}} \)
Given: \(\displaystyle G = 6.674 \times 10^{-11} \, \text{N m}^2 \text{kg}^{-2} \);
M = 3 kg; R = 2 m; x = 2 m
Calculate (V):
\(\displaystyle V = -2 \pi \times 6.674 \times 10^{-11} \frac{3}{\sqrt{2^2 + 2^2}} \)
\(\displaystyle V = -2 \pi\times 6.674 \times 10^{-11} \frac{3}{\sqrt{8}} \)
\(\displaystyle V = -2 \pi \times 6.674 \times 10^{-11} \frac{3}{2.828} \)
\(\displaystyle V = -2 \pi \times 6.674 \times 10^{-11} \times 1.061 \)
\(\displaystyle V \approx -4.455 \times 10^{-10} \, \text{J/kg} \)
Therefore, the gravitational potential at the point (P) is approximately (\(\displaystyle -4.455 \times 10^{-10} \, \text{J/kg} \)).
Problem 7: Calculate the gravitational potential energy of a system of three particles of masses (1 kg), (2 kg), and (3 kg) placed at the vertices of an equilateral triangle of side length (2 m).
Solution: The gravitational potential energy (U) of a system of particles is given by the sum of the potential energies between each pair of particles:
\(\displaystyle U = -G \sum_{i < j} \frac{m_i m_j}{r_{ij}} \)
Given: \(\displaystyle G = 6.674 \times 10^{-11} \, \text{N m}^2 \text{kg}^{-2} \);
Masses: (m1 = 1 kg), (m2 = 2 kg), (m3 = 3 kg); Side length of the equilateral triangle (rij = 2 m)
Calculate (U):
\(\displaystyle U = -G \left( \frac{m_1 m_2}{r_{12}} + \frac{m_2 m_3}{r_{23}} + \frac{m_3 m_1}{r_{31}} \right) \)
\(\displaystyle U = -6.674 \times 10^{-11} \left( \frac{1 \times 2}{2} + \frac{2 \times 3}{2} + \frac{3 \times 1}{2} \right) \)
\(\displaystyle U = -6.674 \times 10^{-11} \left( 1 + 3 + 1.5 \right) \)
\(\displaystyle U = -6.674 \times 10^{-11} \times 5.5 \)
\(\displaystyle U = -3.6707 \times 10^{-10} \, \text{J} \)
Therefore, the gravitational potential energy of the system is (\(\displaystyle -3.6707 \times 10^{-10} \, \text{J} \)).
Problem 8: Calculate the gravitational potential at the center of a uniform spherical shell of mass (8 kg) and radius (4 m).
Solution: The gravitational potential at the center of a spherical shell is the same as at any point on the surface of the shell:
\(\displaystyle V = -G \frac{M}{R} \)
Given: \(\displaystyle G = 6.674 \times 10^{-11} \, \text{N m}^2 \text{kg}^{-2} \); M = 8 kg; R = 4 m
Calculate (V):
\(\displaystyle V = -6.674 \times 10^{-11} \frac{8}{4} \)
\(\displaystyle V = -6.674 \times 10^{-11} \times 2 \)
\(\displaystyle V = -13.348 \times 10^{-11} \, \text{J/kg} \)
Therefore, the gravitational potential at the center of the spherical shell is (\(\displaystyle -13.348 \times 10^{-11} \, \text{J/kg} \).
FAQs
What is gravitational potential energy?
Gravitational potential energy is the energy possessed by an object due to its position in a gravitational field. It represents the work needed to move the object from a reference point, typically at infinity, to a specific point within the field.
How does gravitational potential differ from gravitational potential energy?
Gravitational potential is the gravitational potential energy per unit mass at a specific point in a gravitational field. It represents the work done per unit mass to bring a test mass from infinity to that point, whereas gravitational potential energy is the total work done on an object with mass.
What is the significance of negative values in gravitational potential?
Gravitational potential is often negative because it represents the work done against the gravitational force to bring an object from infinity (where the potential is zero) to a point within the field. A negative potential indicates that work is required to move the object to that point from infinity.
How does gravitational potential change with distance from a mass?
Gravitational potential decreases (becomes more negative) as you move closer to the mass and increases (becomes less negative) as you move away. This means the potential is stronger near the mass and weaker further away.
What is the relationship between gravitational potential and gravitational field strength?
The gravitational field strength at a point is the negative gradient of the gravitational potential at that point. In other words, the gravitational field is the rate of change of gravitational potential with respect to distance. It represents the force experienced by a unit mass at that point.
How does the concept of gravitational potential apply to multiple masses?
When dealing with multiple masses, the gravitational potential at a point is the algebraic sum of the potentials due to each mass. This principle of superposition allows us to calculate the total potential by considering the contributions from all masses in the system.
Why is understanding gravitational potential important in physics?
Understanding gravitational potential is crucial because it simplifies the analysis of gravitational interactions. It helps in calculating the work done by or against gravitational forces, understanding orbital dynamics, and solving problems related to the motion of objects in gravitational fields. It is also essential in fields like astrophysics and cosmology for understanding the behavior of celestial bodies.