Laws of Conservation of Momentum

The concept of momentum conservation has been around since the time of Galileo, but it was Isaac Newton who formalized it in his laws of motion. It’s a principle that has stood the test of time and countless experiments.

The story begins with early philosophers and scientists trying to understand motion. Aristotle had his ideas about motion, but they didn’t quite capture the full picture. It wasn’t until the Middle Ages that scholars like John Philoponus began to challenge these views, setting the stage for later developments.

Galileo Galilei made significant strides in the 17th century. He observed that objects tend to keep moving unless a force acts on them, laying the groundwork for the concept of inertia, which is closely related to momentum.

René Descartes, a contemporary of Galileo, also contributed to the understanding of momentum. He introduced the idea that the total “quantity of motion” (momentum) in the universe is conserved.

The real breakthrough came with Sir Isaac Newton. In his famous work, “Principia Mathematica,” published in 1687, Newton formulated the three laws of motion. The first law, also known as the law of inertia, implies the conservation of momentum. His third law, stating that every action has an equal and opposite reaction, provides the foundation for the conservation of momentum during interactions between bodies.

Newton’s laws made it clear that in the absence of external forces, the total momentum of a system remains constant. This principle was revolutionary and has been confirmed by countless experiments over the centuries.

Today, the conservation of momentum is a cornerstone of physics. It’s used in everything from predicting the outcomes of particle collisions in accelerators to understanding the dynamics of galaxies in the universe.

What is Momentum

Momentum is a fundamental concept in physics that helps us describe and understand the motion of objects. It plays a crucial role in many areas of physics, from mechanics to collisions and even quantum mechanics. Momentum is a measure of how hard it is to stop a moving object. In simple terms, momentum can be thought of as the “push” or “drive” that an object has when it’s in motion.

Momentum is defined as the product of an object’s mass and its velocity. Mathematically, it can be expressed as:

\(\displaystyle \text{Momentum} = \text{Mass} \times \text{Velocity} \)

The unit of momentum is kilogram-meter per second (kg m/s), where kilogram (kg) represents the mass of the object and meter per second (m/s) represents its velocity.

Mass: Mass refers to the amount of matter in an object. It’s a measure of how much “stuff” is packed into an object. The more massive an object is, the more momentum it has.

Velocity: Velocity describes the speed of an object in a particular direction. It’s a measure of how fast and in which direction an object is moving. Objects moving faster or with higher velocities have more momentum.

One important aspect of momentum is that it’s a vector quantity, meaning it has both magnitude and direction. The direction of an object’s momentum is the same as the direction of its velocity. For example, if an object is moving to the right, its momentum is also pointing to the right.

Momentum is a fundamental concept in physics because it helps us understand and predict how objects will move and interact. Whether it’s cars crashing, rockets launching, or just you throwing a ball, momentum is at play.

Momentum Conservation Principle

The principle of momentum conservation states that if no external forces act on a group of objects, their total momentum stays the same. This means that the momentum before any event, like a collision, is equal to the momentum after the event.

The Momentum Conservation Principle is like a cosmic rule that says, “What you have, you keep.” In physics terms, it means that within a closed system, the total amount of momentum is always the same—it doesn’t change unless something from outside the system messes with it.

First, remember that momentum is a combination of how much stuff an object has (mass) and how fast it’s going (velocity). It’s a vector, which means it has both size and direction.

Imagine you’re playing air hockey. When the two pucks collide, they push against each other and bounce off. Before they hit, they had some momentum, and after they bounced away, they still had momentum. The cool part? If you add up all the momentum before and after, it’s the same.

This principle only works perfectly when there are no external forces. That means no friction, no air resistance, nothing that’s not part of the system. In real life, we usually have some forces acting, but in many situations, they’re small enough that we can still use the principle to make accurate predictions.

It all comes down to Newton’s Third Law of Motion: for every action, there’s an equal and opposite reaction. When two objects interact, like in a collision, they push against each other equally and oppositely, so the total momentum stays constant.

\(\displaystyle\begin{equation}\label{eqn:1}\boxed{\boldsymbol{ m_{1} \times v_{1} + m_{2} \times v_{2} = m_{1} \times v’_{1} + m_{2} \times v’_{2}}} \end{equation}\)

This equation says that the total momentum before the collision \(\displaystyle (m_{1} \times v_{1} + m_{2} \times v_{2} \)) is the same as the total momentum after the collision \(\displaystyle( m_{1} \times v’_{1} + m_{2} \times v’_{2} \)),
where (m) is mass, (v) is velocity, and the primes (‘) indicate the velocities after the collision.

Think about a game of pool again. When the cue ball hits another ball, they exchange momentum. The total momentum of the balls before the hit is the same as the total momentum after, even though the individual momenta of the balls have changed.

Conservation of Linear Momentum

Linear momentum is momentum in a straight line. The conservation of linear momentum says that in a closed system (where no external forces interfere), the total linear momentum doesn’t change. This is true for all interactions, not just collisions.

Linear momentum, often simply called momentum, is a measure of an object’s motion. It is calculated by multiplying the object’s mass (how much matter it contains) by its velocity (the speed and direction it’s moving). The formula looks like this:

\(\displaystyle p = m \times v \)

Here, (p) represents momentum, (m) is the mass, and (v) is the velocity. The SI unit for momentum is kilogram meters per second (kg·m/s).

Now, the Conservation of Linear Momentum states that within an isolated system (a group of interacting objects not affected by external forces), the total momentum remains constant over time. This means that the total amount of momentum before any event, like a collision, is equal to the total amount of momentum after the event. Mathematically, the conservation of linear momentum can be expressed as follows:

If the initial momentum of the system is (p_i) and the final momentum is (p_f), then:

\(\displaystyle p_{i} = p_{f} \)

This equation tells us that the momentum of the system before an event (like a collision) is equal to the momentum of the system after the event, provided no external forces act on it.

A practical example of this principle is a game of pool. When the cue ball strikes another ball, the total momentum of both balls before the collision is the same as the total momentum after the collision. The cue ball may slow down, but the ball it hits will move away with the momentum the cue ball transferred to it.

Derivation of Conservation of Momentum

We begin with Newton’s Third Law of Motion, which tells us that for every action, there’s an equal and opposite reaction. This means that if two objects collide, the force one object exerts on the other is equal in magnitude and opposite in direction to the force exerted back.

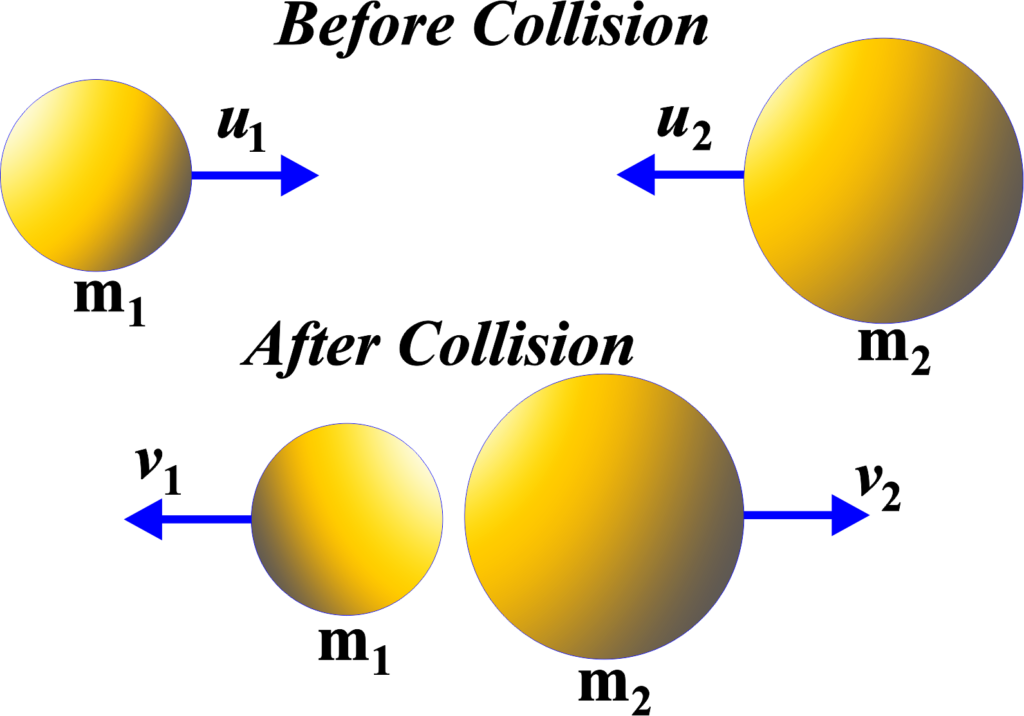
Imagine two objects, A and B, with masses (m₁) and (m₂), moving towards each other with velocities (u₁) and (u₂). They collide, and after the collision, their velocities change to (v₁) and (v₂).

During the collision, object A exerts a force on object B for a certain amount of time, resulting in a change in momentum for object B. Similarly, object B exerts an equal and opposite force on object A, causing a change in momentum for object A.

Let’s denote the force that A exerts on B as (F_AB) and the force that B exerts on A as (F_BA). According to Newton’s Third Law, (F_AB = -F_BA).

The change in momentum for object A is given by:

\(\displaystyle \Delta p_{A} = m_{1} (v_{1} – u_{1}) \)

And for object B:

\(\displaystyle \Delta p_{B} = m_{2} (v_{2} – u_{2}) \)

Since the forces are equal and opposite, and they act for the same amount of time, the changes in momentum are also equal and opposite:

\(\displaystyle m_{1} (v_{1} – u_{1}) = -m_{2} (v_{2} – u_{2}) \)

If we rearrange the equation, we get:

\(\displaystyle\begin{equation}\label{eqn:2}\boxed{\boldsymbol{m_{1} u_{1} + m_{2} u_{2} = m_{1} v_{1} + m_{2} v_{2} }} \end{equation}\)

This equation tells us that the total momentum before the collision \(\displaystyle( m_{1} u_{1} + m_{2} u_{2} \)) is equal to the total momentum after the collision \(\displaystyle( m_{1} v_{1} + m_{2} v_{2} \)), proving that momentum is conserved.

The derivation shows that in the absence of external forces, the total momentum of a system remains constant, no matter what happens inside the system.

Why is Momentum Conserved?

The conservation of momentum is deeply rooted in Newton’s Third Law of Motion. This law states that for every action, there’s an equal and opposite reaction¹. When two objects interact, like during a collision, they exert forces on each other that are equal in magnitude but opposite in direction.

Let’s say you have two ice skaters pushing off from each other. Skater A exerts a force on Skater B, and Skater B exerts an equal and opposite force on Skater A. These forces are applied for the same amount of time, so the changes in their momenta are equal and opposite.

If we use (F) to represent force and (∆v) to represent the change in velocity, then the change in momentum (∆p) for each skater can be described as:

\(\displaystyle \Delta p = F \times \Delta t \)

where (∆t) is the time during which the force is applied. Since the forces are equal and opposite, the changes in momentum cancel each other out, keeping the total momentum the same.

In a closed system, where no external forces are acting, the total momentum before any event is equal to the total momentum after the event. This is because the internal forces within the system (like the forces the skaters exert on each other) don’t change the total momentum—they just redistribute it among the objects in the system.

During collisions, whether they’re elastic (bouncy) or inelastic (sticky), the total momentum of the colliding bodies remains constant. This is because the forces involved are internal to the system of those bodies.

For momentum to be conserved, the system must be isolated, meaning no external forces (like friction or air resistance) are acting on it. In real-life situations, these forces can affect momentum, but in many physics problems, we assume they’re negligible to simplify the calculations.

Example of Conservation of Momentum

Imagine a balloon filled with air. Inside the balloon, countless tiny gas particles are moving rapidly in all directions. These particles collide with each other and with the walls of the balloon. During these collisions, particles exchange momentum: some speed up, some slow down, but the total momentum of all the particles inside the balloon remains constant.

This happens because no external forces are acting on the system of gas particles inside the balloon. The balloon’s elastic surface provides an internal boundary, so the momentum is transferred back and forth between particles but not lost or gained overall.

Let’s break it down further:

• Before Collision: Particle A is moving to the right with a certain momentum, and Particle B is moving to the left with its momentum.
• During Collision: Particle A hits Particle B. They exert equal and opposite forces on each other (thanks to Newton’s Third Law).
• After Collision: Particle A moves to the left, and Particle B moves to the right. Their speeds may change, but the total momentum of Particle A plus Particle B remains the same as it was before the collision.

If we were to put numbers to it, we could say Particle A has a mass of (m_A) and a velocity of (v_A), and Particle B has a mass of (m_B) and a velocity of (v_B). The total momentum before the collision (p_{total, before}) is:

\(\displaystyle p_{total, before} = m_{A} \times v_{A} + m_{B} \times v_{B} \)

After the collision, their velocities change to ( v’_A) and ( v’_B), but the total momentum (p _{total, after}) is still:

\(\displaystyle p_{total, after} = m_{A} \times v’_{A} + m_{B} \times v’_{B} \)

According to the principle of conservation of momentum:

\(\displaystyle p_{total, before} = p_{total, after} \)

This example shows that in a closed system, the total momentum is conserved.

Other Examples

• Air-filled Balloons: When you release the air from a balloon, the air rushes out in one direction, and the balloon moves in the opposite direction. This is due to the conservation of momentum. The momentum of the air going one way is equal to the momentum of the balloon going the other way.
• System of Gun and Bullet: When a gun is fired, the bullet moves forward, and the gun recoils backward. The forward momentum of the bullet is equal to the backward momentum of the gun, ensuring that the total momentum before and after firing is conserved.
• Motion of Rockets: Rockets move forward by expelling exhaust gases backward at high speed. The momentum of the rocket moving forward is equal to the momentum of the exhaust gases going backward, demonstrating the conservation of momentum in action.
• Newton’s Cradle: A Newton’s Cradle is a device with a series of swinging spheres. When one sphere at the end is lifted and released, it strikes the stationary spheres, and a sphere at the opposite end swings upward. The momentum is transferred through the spheres, showing the conservation of momentum.
• Collision of Two Objects: When two objects collide, such as two cars in a bumper-to-bumper accident, the total momentum of the two cars before the collision is equal to their total momentum after the collision, assuming no external forces like friction are acting on them.
• Ice Skater: An ice skater spinning with arms outstretched will spin faster when they pull their arms in. The skater’s momentum is conserved, but the distribution of mass changes, which affects the rotation speed.

Also Read: Law of Inertia

Application of the Law of Conservation of Momentum

Vehicle Collisions: In car accidents, the conservation of momentum is used to analyze the collision. By examining the momentum before and after the crash, investigators can determine the velocities of the vehicles involved and reconstruct the accident.

Rocket Propulsion: Rockets in space propel themselves by expelling gas out of their engines. The momentum of the gas going one way gives the rocket momentum in the opposite direction, allowing it to move through space.

Sports: In sports like billiards or ice hockey, players use the conservation of momentum to predict where the balls or pucks will go after they collide. This helps them make strategic plays.

Explosions: When an explosion occurs, the total momentum of all the fragments just after the explosion is equal to the momentum before the explosion, which is usually zero if the bomb is at rest. This principle helps forensic experts understand the nature of the explosion.

Particle Physics: In particle accelerators, scientists collide particles at high speeds. The conservation of momentum allows them to predict the paths of particles after the collision, which is crucial for discovering new particles and understanding fundamental forces.

Astrophysics: The momentum conservation law helps astrophysicists understand the behavior of celestial bodies. For example, when a star explodes as a supernova, the core may recoil, conserving the momentum of the ejected outer layers.

Technology Development: Engineers use momentum conservation principles to design safer vehicles, sports equipment, and even protective gear like helmets, ensuring that the forces during an impact are distributed in a way that minimizes injury.

Solved Examples

Problem 1: Two balls of masses 2 kg and 3 kg are moving towards each other with speeds of 4 m/s and 2 m/s respectively. Calculate their velocities after a head-on elastic collision.

Solution: Using the conservation of momentum and kinetic energy for an elastic collision:

Let (u₁ = 4 m/s) (velocity of 2 kg mass), (u₂ = -2 m/s) (velocity of 3 kg mass), (m₁ = 2 kg), and (m₂ = 3 kg).

The final velocities (v₁) and (v₂) are given by:

\(\displaystyle v_1 = \frac{(m_1 – m_2)u_1 + 2m_2u_2}{m_1 + m_2} \)
\(\displaystyle v_2 = \frac{(m_2 – m_1)u_2 + 2m_1u_1}{m_1 + m_2} \)

Substitute the values:

\(\displaystyle v_1 = \frac{(2 – 3) \times 4 + 2 \times 3 \times (-2)}{2 + 3} \)
\(\displaystyle v_1 = \frac{-4 – 12}{5} \)
\(\displaystyle v_1 = \frac{-16}{5} = -3.2 \, \text{m/s} \)

\(\displaystyle v_2 = \frac{(3 – 2) \times (-2) + 2 \times 2 \times 4}{2 + 3} \)
\(\displaystyle v_2 = \frac{-2 + 16}{5} \)
\(\displaystyle v_2 = \frac{14}{5} = 2.8 \, \text{m/s} \)

After the collision, the velocities of the 2 kg and 3 kg masses are -3.2 m/s and 2.8 m/s, respectively.

Problem 2: A 5 kg cart moving at 6 m/s collides with a stationary 10 kg cart. After the collision, they stick together. Find their common velocity.

Solution: Using the conservation of momentum for an inelastic collision:

Let (m₁ = 5 kg), (u₁ = 6 m/s), (m₂ = 10 kg), and (u₂ = 0 m/s).

The common velocity (v) after a collision is:

\(\displaystyle (m_1 + m_2)v = m_1u_1 + m_2u_2 \)
\(\displaystyle (5 + 10)v = 5 \times 6 + 10 \times 0 \)
15v = 30
\(\displaystyle v = \frac{30}{15} = 2 \, \text{m/s} \)

The common velocity after the collision is 2 m/s.

Problem 3: A stationary bomb of mass 10 kg explodes into two fragments of masses 4 kg and 6 kg. The 4 kg fragment moves with a velocity of 15 m/s. Find the velocity of the 6 kg fragment.

Solution: Using the conservation of momentum for an explosion:

Let (m₁ = 4 kg), (v₁ = 15 m/s), (m₂ = 6 kg), and (v₂) be the velocity of the 6 kg fragment.

Since the initial momentum is zero (the bomb was stationary):

\(\displaystyle 0 = m_1v_1 + m_2v_2 \)
\(\displaystyle 0 = 4 \times 15 + 6 \times v_2 \)
\(\displaystyle 0 = 60 + 6v_2 \)
\(\displaystyle v_2 = -\frac{60}{6} = -10 \, \text{m/s} \)

The velocity of the 6 kg fragment is -10 m/s.

Problem 4: A 2 kg ball is thrown against a wall with a velocity of 8 m/s and rebounds with a velocity of 6 m/s. Calculate the impulse exerted by the wall on the ball.

Solution: Impulse (J) is given by the change in momentum:

\(\displaystyle J = \Delta p = m(v_f – v_i) \)

Let (m = 2 kg, (v_i = 8 m/s), (v_f = -6 m/s) (rebound direction is opposite).

\(\displaystyle J = 2 \times (-6 – 8) \)
\(\displaystyle J = 2 \times (-14) \)
J = -28 Ns

The impulse exerted by the wall on the ball is -28 Ns.

Problem 5: A 3 kg ball moving at 4 m/s collides with a 5 kg ball moving at 2 m/s in the same direction. After the collision, the 3 kg ball moves at 3 m/s in the same direction. Find the velocity of the 5 kg ball after the collision.

Solution: Using the conservation of momentum:

Let (m₁ = 3 kg), (u₁ = 4 m/s), (m₂ = 5 kg), (u₂ = 2 m/s), and (v₁ = 3 m/s).

The final velocity of the 5 kg ball (v₂) is:

\(\displaystyle m_1u_1 + m_2u_2 = m_1v_1 + m_2v_2 \)
\(\displaystyle 3 \times 4 + 5 \times 2 = 3 \times 3 + 5 \times v_2 \)
\(\displaystyle 12 + 10 = 9 + 5v_2 \)
\(\displaystyle 22 = 9 + 5v_2 \)
\(\displaystyle 5v_2 = 13 \)
\(\displaystyle v_2 = \frac{13}{5} = 2.6 \, \text{m/s} \)

The velocity of the 5 kg ball after the collision is 2.6 m/s.

Problem 6: A 4 kg block moving at 5 m/s collides with a stationary 6 kg block and sticks to it. Calculate the velocity of the combined blocks after the collision.

Solution: Using the conservation of momentum for the system:

Let (m₁ = 4 kg), (u₁ = 5 m/s), (m₂ = 6 kg), and (u₂ = 0 m/s).

The velocity (v) of the combined mass after collision is:

\(\displaystyle(m_1 + m_2)v = m_1u_1 + m_2u_2 \)
\(\displaystyle (4 + 6)v = 4 \times 5 + 6 \times 0 \)
10v = 20
\(\displaystyle v = \frac{20}{10} = 2 \, \text{m/s} \)

The velocity of the combined blocks after the collision is 2 m/s.

FAQs