The journey of the Lens Maker’s Formula begins with the craft of lens making, which dates back to the 13th century. However, the scientific understanding of how lenses work evolved much later. The formula itself was not the work of a single individual but rather the culmination of efforts by many scientists and lens makers over the centuries.
The development of the Lens Maker’s Formula is closely tied to the advancement of the field of optics. In the 17th century, Sir Isaac Newton made significant contributions to the study of light and lenses, although he did not derive the formula himself. It was through collective experimentation and observations by lens makers that the relationship between the physical parameters of lenses and their optical properties was understood.
These early lens makers were skilled craftsmen who meticulously shaped glass into lenses, relying on trial and error to achieve the desired focal lengths for various applications. They observed that the curvature of the lens surfaces and the type of glass used affected how light was bent, or refracted, as it passed through the lens.
As the demand for more precise lenses grew, especially with the advent of scientific instruments like telescopes and microscopes, there was a need for a more systematic approach to lens design. This led to the derivation of the Lens Maker’s Formula, which provided a mathematical way to calculate the focal length of a lens based on its shape and the refractive index of the material from which it was made.
The formula revolutionized lens manufacturing by allowing lens makers to predict the optical behavior of a lens without the need for extensive trial and error. This was particularly important for producing corrective lenses for eyeglasses, which needed to be tailored to the specific vision needs of individuals.
What is the Thin Lens Formula?
The Thin Lens Formula is a simple yet powerful tool in optics that relates the distances of the object and the image to the focal length of a lens. It’s given by the equation:
\(\displaystyle \frac{1}{f} = \frac{1}{v} + \frac{1}{u} \)
- f is the focal length of the lens, which is the distance from the lens where parallel rays of light converge or appear to diverge from.
- v is the image distance, the distance from the lens to the image formed by the lens.
- u is the object distance, the distance from the lens to the object being viewed.
The beauty of this formula lies in its ability to predict where an image will form when light passes through a lens. It tells us that if we know two of these distances (object, image, or focal length), we can calculate the third.
For a converging lens (like a magnifying glass), parallel rays of light are brought together (converge) at the focal point. For a diverging lens (like those used in eyeglasses for nearsightedness), parallel rays of light are spread out (diverge) and seem to come from a point called the virtual focal point.
Imagine you’re holding a magnifying glass (a converging lens) and you want to focus sunlight onto a piece of paper to start a fire. You adjust the distance between the magnifying glass and the paper until you find the sharpest point of light. This point is where the image of the sun (which is very far away, so we consider it at infinity) is focused, and this distance is the focal length of your magnifying glass.
What is Lens Maker’s Formula?
The Lens Maker’s Formula is an equation used to calculate the focal length of a lens based on its refractive index (n) and the radii of curvature (R1 and R2) of its surfaces. The Lens Maker’s Formula is a crucial equation in optics that allows us to calculate the focal length of a lens. The focal length is essentially how strong the lens is in bending light. This formula is particularly special because it tells us the focal length based on the shape of the lens and the type of material the lens is made from.
\(\displaystyle \frac{1}{f} = (n – 1) \left( \frac{1}{R_1} – \frac{1}{R_2} \right) \)
- f is the focal length of the lens.
- n is the refractive index of the material of the lens.
- R₁ and R₂ are the radii of curvature of the lens’s two surfaces.
- The refractive index (n) tells us how much the material of the lens can bend light. For example, glass has a different refractive index than plastic.
- The radii of curvature (R₁ and R₂) describe the shape of the lens surfaces. If you think of each surface as part of a sphere, the radius of that sphere is what we’re talking about here.
Imagine you’re designing a pair of glasses. You need to know how strong the lenses should be to correct someone’s vision. By using the Lens Maker’s Formula, you can figure out exactly how to shape the lens and what material to use so that it has the right focal length to help that person see clearly.
Derivation of Lens Maker’s Formula
The derivation of the Lens Maker’s Formula involves considering a thin lens with two refracting surfaces. By applying the laws of refraction at each surface and assuming the lens is thin, we arrive at the formula mentioned above. The detailed steps involve using the refraction formula for spherical surfaces and combining them to eliminate the intermediate variables.
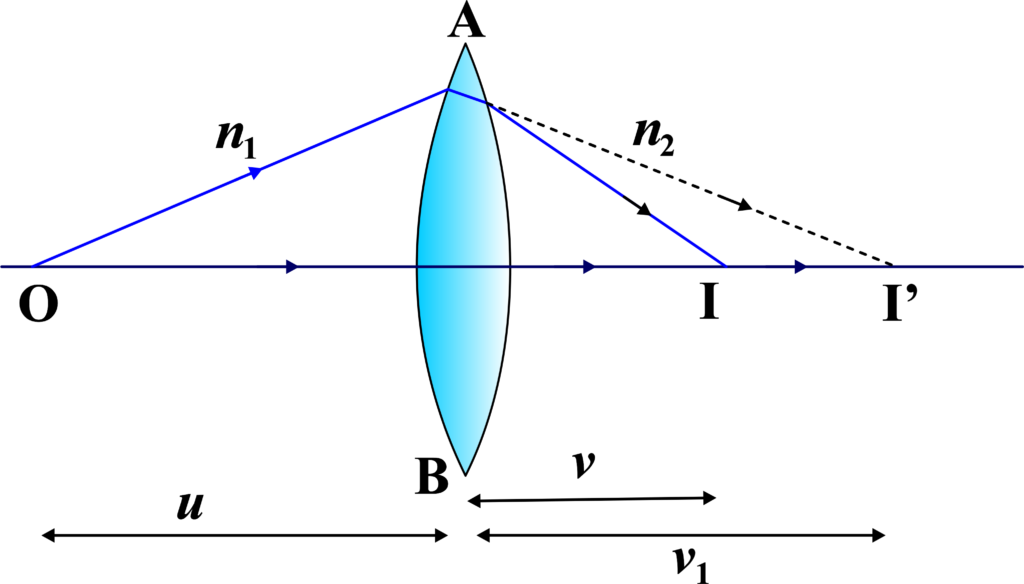
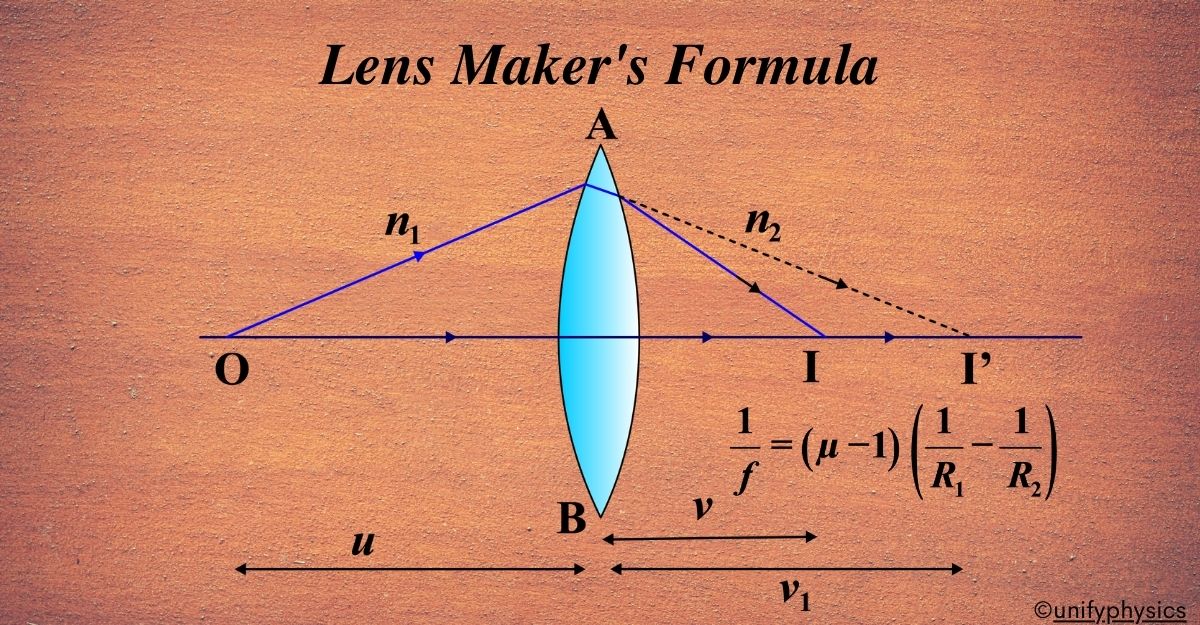
Consider a thin lens with two refracting surfaces. Let the refractive indices of the surrounding medium and the lens material be n₁ and n₂, respectively. The radii of curvature of the two surfaces are R₁ and R₂.
Apply the formula for refraction at a single spherical surface to the first surface:
\(\displaystyle \frac{n₂}{v₁} – \frac{n₁}{u} = \frac{n₂ – n₁}{R₁} \quad \text{(1)} \)
Here, u is the object distance, and v₁ is the image distance formed by the first surface.
Now consider the second surface. The image formed by the first surface acts as the object for the second surface. Apply the same formula for refraction to the second surface:
\(\displaystyle \frac{n₁}{v} – \frac{n₂}{v₁} = \frac{n₁ – n₂}{R₂} \quad \text{(2)} \)
Here, v is the image distance formed by the entire lens. Add equations (1) and (2):
\(\displaystyle \frac{1}{v} – \frac{1}{u} = \left(\frac{n₂}{n₁} – 1\right) \left(\frac{1}{R₁} – \frac{1}{R₂}\right) \)
When u = ∞ (object at infinity) and v = f (focal length), we get:
\(\displaystyle \frac{1}{f} = \left(\frac{n₂}{n₁} – 1\right) \left(\frac{1}{R₁} – \frac{1}{R₂}\right) \)
Let μ represent the refractive index of the material (i.e., μ = n₂/n₁). The Lens Maker’s Formula is:
\(\displaystyle \frac{1}{f} = (\mu – 1) \left(\frac{1}{R₁} – \frac{1}{R₂}\right) \)
This formula allows lens manufacturers to design lenses with specific focal lengths for various applications. It’s a powerful tool in optics, helping us create lenses for cameras, telescopes, eyeglasses, and more. Remember, the lens should be thin, and the medium on both sides of the lens should be the same for this formula to hold.
Lens Maker’s Formula for (Convex Lens)
The Lens Maker’s Formula for a convex lens helps us determine the focal length of the lens based on its physical properties. A convex lens is thicker in the middle and thinner at the edges, causing light rays to converge.
\(\displaystyle \frac{1}{f} = (n – 1) \left( \frac{1}{R_1} – \frac{1}{R_2} \right) \)
The refractive index (n) indicates how much the lens material can bend light. A higher refractive index means the material can bend light more. The radii of curvature (R₁ and R₂) describe the curvature of the lens surfaces. For a convex lens, R₁ is positive, indicating the center of curvature is on the opposite side of the incoming light, and R₂ is negative, indicating the center of curvature is on the same side as the incoming light.
Imagine a beam of light hitting a convex lens. The lens’s shape and material will bend the light rays so that they meet at a point known as the focal point. The distance from the center of the lens to this focal point is the focal length (f), which we can calculate using the Lens Maker’s Formula.
Lens Maker’s Formula for a Concave Lens
A concave lens is designed to diverge light rays, and it’s thinner in the middle than at the edges. The Lens Maker’s Formula for a concave lens allows us to calculate its focal length based on the shape of the lens and the material it’s made from.
\(\displaystyle \frac{1}{f} = (n – 1) \left( \frac{1}{-R_1} + \frac{1}{R_2} \right) \)
The refractive index (n) tells us how much the lens material bends light. For example, glass has a different refractive index than plastic. The radii of curvature (R₁ and R₂) describe the curvature of the lens surfaces. For a concave lens, R₁ is negative because the center of curvature is on the same side as the incoming light, and R₂ is positive because the center of curvature is on the opposite side.
When light hits a concave lens, the shape and material of the lens cause the light rays to spread out. This divergence means that the light rays appear to come from a point known as the focal point, which is located on the same side of the lens as the incoming light. The distance from the lens to this focal point is the negative focal length (f), which we can find using the Lens Maker’s Formula.
Lens Maker’s Formula for a Thick Lens
When dealing with a thick lens, the Lens Maker’s Formula is modified to account for the lens’s thickness. The formula for a thick lens takes into consideration the distance between the two lens surfaces, which is known as the lens thickness (d). The Lens Maker’s Formula for a thin lens is:
\(\displaystyle \frac{1}{f} = (n – 1) \left( \frac{1}{R_1} – \frac{1}{R_2} \right) \)
Where f is the focal length, n is the refractive index, and R₁ and R₂ are the radii of curvature of the lens surfaces.
For a thick lens, we need to consider the lens’s thickness (d) in addition to the radii of curvature and refractive index. The presence of thickness means that light rays travel an additional optical path within the lens material. This additional path affects the lens’s ability to converge or diverge light, altering the focal length. The modified Lens Maker’s Formula for a thick lens includes an extra term to account for the lens thickness:
\(\displaystyle \frac{1}{f} = (n – 1) \left( \frac{1}{R_1} – \frac{1}{R_2} + \frac{(n – 1)d}{nR_1R_2} \right) \)
The term \(\displaystyle \frac{(n – 1)d}{nR_1R_2} \) represents the correction due to the lens’s thickness. This term becomes significant when the lens thickness is not negligible compared to the size of the radii of curvature. It’s derived from considering the actual path light takes through the lens material, which is longer for a thick lens than for a thin lens. When using this formula, you’ll calculate a different focal length for a thick lens compared to a thin lens, even if all other factors (like the refractive index and radii of curvature) are the same.
Also Read: Combination of Thin Lenses in Contact
Sign Conventions for Lens Maker’s Formula
When using the Lens Maker’s Formula, we follow a set of rules known as sign conventions to determine the signs (+ or -) for the values we plug into the formula. These conventions are based on the Cartesian coordinate system and are consistent with the conventions used in ray optics. Here are the key sign conventions:
Focal Length (f):
- For a convex lens, the focal length is positive because it converges light to a real focus.
- For a concave lens, the focal length is negative because it diverges light, and the focus is virtual.
Radii of Curvature (R₁ and R₂):
- The radius of curvature is positive if the center of curvature is on the same side as the light is coming from (after refraction).
- It is negative if the center of curvature is on the opposite side.
Refractive Index (n):
- The refractive index is always positive since it’s a ratio of the speed of light in a vacuum to that in the medium and is always greater than one.
By following these conventions, students can accurately calculate the focal length of lenses using the Lens Maker’s Formula. It’s important to remember these rules while solving problems in optics to avoid errors in the sign, which can lead to incorrect results. So, when you’re working with the Lens Maker’s Formula:
\(\displaystyle \frac{1}{f} = (n – 1) \left( \frac{1}{R_1} – \frac{1}{R_2} \right) \)
Make sure to apply the correct signs to the radii of curvature based on where the centers of curvature lie in relation to the lens, and remember that the focal length’s sign will tell you whether the lens is converging or diverging.
Applications of Lens Maker’s Formula
The Lens Maker’s Formula has numerous applications in optics. It is used by engineers and scientists to design and manufacture lenses with specific focal lengths for various applications such as cameras, telescopes, microscopes, and eyeglasses. It also plays a critical role in the production of corrective lenses for eyeglasses and the design of camera lenses for sharp and clear images.
- Designing Corrective Eyeglasses: Optometrists use the Lens Maker’s Formula to determine the correct curvature needed for eyeglass lenses to correct vision problems like myopia or hyperopia. By knowing a patient’s vision prescription, which includes the focal length, they can design lenses that will help focus light correctly onto the retina.
- Camera Lenses: Camera manufacturers rely on this formula to design lenses that produce sharp and clear images. The formula helps in calculating the precise curvature needed for lenses to focus light onto the camera sensor or film.
- Telescopes and Microscopes: The Lens Maker’s Formula is essential in designing the lenses for telescopes and microscopes, allowing astronomers and scientists to view distant stars or tiny cells in detail. The focal length determined by the formula is critical for magnifying distant or small objects.
- Manufacturing Lenses with Specific Properties: Lens makers use this formula to create lenses with desired focal lengths for various applications, from scientific instruments to everyday gadgets. Knowing the material’s refractive index and the required focal length, they can shape the lens accordingly.
Solved Examples
Example 1: An object is placed 30 cm from a convex lens of focal length 20 cm. Determine the position and nature of the image formed.
Solution: We use the thin lens formula:
\(\displaystyle\frac{1}{f} = \frac{1}{v} – \frac{1}{u}\)
Substitute the values:
\(\displaystyle\frac{1}{20} = \frac{1}{v} – \frac{1}{-30}\)
\(\displaystyle\frac{1}{20} = \frac{1}{v} + \frac{1}{30}\)
\(\displaystyle\frac{1}{v} = \frac{1}{20} – \frac{1}{30}\)
\(\displaystyle\frac{1}{v} = \frac{3 – 2}{60}\)
\(\displaystyle\frac{1}{v} = \frac{1}{60}\)
\(\displaystyle v = 60 \text{ cm}\)
The image is formed 60 cm on the opposite side of the lens, indicating a real, inverted, and magnified image.
Example 2: An object is placed 25 cm from a concave lens of focal length -15 cm. Determine the position and nature of the image formed.
Solution: We use the thin lens formula:
\(\displaystyle\frac{1}{f} = \frac{1}{v} – \frac{1}{u}\)
Substitute the values:
\(\displaystyle\frac{1}{-15} = \frac{1}{v} – \frac{1}{-25}\)
\(\displaystyle\frac{1}{-15} = \frac{1}{v} + \frac{1}{25}\)
\(\displaystyle\frac{1}{v} = \frac{1}{-15} – \frac{1}{25}\)
\(\displaystyle\frac{1}{v} = \frac{-5 – 3}{75}\)
\(\displaystyle\frac{1}{v} = \frac{-8}{75}\)
\(\displaystyle v = -\frac{75}{8} \approx -9.375 \text{ cm}\)
The image is formed approximately 9.375 cm on the same side of the lens as the object, indicating a virtual, upright, and reduced image.
Example 3: Calculate the focal length of a convex lens made of glass (n = 1.5) with radii of curvature (R1 = 20 cm) and (R2 = -30 cm).
Solution: We use the lens maker’s formula:
\(\displaystyle\frac{1}{f} = (n – 1) \left( \frac{1}{R_1} – \frac{1}{R_2} \right)\)
Substitute the values:
\(\displaystyle\frac{1}{f} = (1.5 – 1) \left( \frac{1}{20} – \frac{1}{-30} \right)\)
\(\displaystyle\frac{1}{f} = 0.5 \left( \frac{1}{20} + \frac{1}{30} \right)\)
\(\displaystyle\frac{1}{f} = 0.5 \left( \frac{3 + 2}{60} \right)\)
\(\displaystyle\frac{1}{f} = 0.5 \left( \frac{5}{60} \right)\)
\(\displaystyle\frac{1}{f} = 0.5 \left( \frac{1}{12} \right)\)
\(\displaystyle\frac{1}{f} = \frac{1}{24}\)
\(\displaystyle f = 24 \text{ cm}\)
The focal length of the convex lens is 24 cm.
Example 4: A convex lens has radii of curvature (R1 = 15 cm) and (R2 = -20 m) and a focal length of 10 cm. Calculate the refractive index of the lens material.
Solution: We use the lens maker’s formula and solve for (n):
\(\displaystyle\frac{1}{f} = (n – 1) \left( \frac{1}{R_1} – \frac{1}{R_2} \right)\)
Substitute the values:
\(\displaystyle\frac{1}{10} = (n – 1) \left( \frac{1}{15} – \frac{1}{-20} \right)\)
\(\displaystyle\frac{1}{10} = (n – 1) \left( \frac{1}{15} + \frac{1}{20} \right)\)
\(\displaystyle\frac{1}{10} = (n – 1) \left( \frac{4 + 3}{60} \right)\)
\(\displaystyle\frac{1}{10} = (n – 1) \left( \frac{7}{60} \right)\)
\(\displaystyle\frac{1}{10} = (n – 1) \left( \frac{7}{60} \right)\)
\(\displaystyle\frac{1}{10} = \frac{7(n – 1)}{60}\)
\(\displaystyle\frac{60}{10} = 7(n – 1)\)
\(\displaystyle 6 = 7(n – 1)\)
\(\displaystyle 6 = 7n – 7\)
\(\displaystyle 7n = 13\)
\(\displaystyle n = \frac{13}{7} \approx 1.86\)
The refractive index of the lens material is approximately 1.86.
Example 5: A lens is made by combining a convex lens of focal length 12 cm and a concave lens of focal length 18 cm in contact. Using the lens maker’s formula, determine the effective focal length of the combination if both lenses are made of the same material with (n = 1.5) and have the same radii of curvature (R1 =10 cm) and (R2 = -10 cm).
Solution: First, use the lens maker’s formula to calculate the focal lengths individually.
For the convex lens:
\(\displaystyle\frac{1}{f_1} = (n – 1) \left( \frac{1}{R_1} – \frac{1}{R_2} \right)\)
\(\displaystyle\frac{1}{12} = (1.5 – 1) \left( \frac{1}{10} – \frac{1}{-10} \right)\)
\(\displaystyle\frac{1}{12} = 0.5 \left( \frac{1}{10} + \frac{1}{10} \right)\)
\(\displaystyle\frac{1}{12} = 0.5 \left( \frac{2}{10} \right)\)
\(\displaystyle\frac{1}{12} = 0.5 \left( \frac{1}{5} \right)\)
\(\displaystyle\frac{1}{12} = \frac{0.5}{5} = \frac{1}{10}\)
This confirms the given focal length of 12 cm.
For the concave lens:
\(\displaystyle\frac{1}{f_2} = (n – 1) \left( \frac{1}{R_1} – \frac{1}{R_2} \right)\)
\(\displaystyle\frac{1}{18} = (1.5 – 1) \left( \frac{1}{10} – \frac{1}{-10} \right)\)
\(\displaystyle\frac{1}{18} = 0.5 \left( \frac{1}{10} + \frac{1}{10} \right)\)
\(\displaystyle\frac{1}{18} = 0.5 \left( \frac{2}{10} \right)\)
\(\displaystyle\frac{1}{18} = 0.5 \left( \frac{1}{5} \right)\)
\(\displaystyle\frac{1}{18} = \frac{0.5}{5} = \frac{1}{10}\)
This confirms the given focal length of 18 cm.
Now, calculate the combined focal length (F) using:
\(\displaystyle\frac{1}{F} = \frac{1}{f_1} + \frac{1}{f_2}\)
Substitute the values:
\(\displaystyle\frac{1}{F} = \frac{1}{12} + \frac{1}{-18}\)
\(\displaystyle\frac{1}{F} = \frac{3 – 2}{36}\)
\(\displaystyle\frac{1}{F} = \frac{1}{36}\)
\(\displaystyle F = 36 \text{ cm}\)
The effective focal length of the combination is 36 cm.
FAQs
What is the thin lens formula and what is its significance in optics?
The thin lens formula relates the object distance, image distance, and focal length of a lens. It is significant because it allows us to determine the position and nature of the image formed by a thin lens, whether it is real or virtual, magnified or diminished, and inverted or upright. This formula is fundamental in the design and analysis of optical systems.
What is the lens maker’s formula and why is it used?
The lens maker’s formula is used to calculate the focal length of a lens based on its radius of curvature and the refractive index of the lens material. It is crucial for lens manufacturing, as it helps lens makers design lenses with specific optical properties required for various applications, such as eyeglasses, cameras, and microscopes.
How is the lens maker’s formula applied to a convex lens?
For a convex lens, the lens maker’s formula considers the curvature of both the lens surfaces and the material’s refractive index. Since convex lenses are thicker at the center, they converge light rays to a focal point. The formula helps design convex lenses with the desired focal length to achieve specific magnification and focusing properties.
How is the lens maker’s formula applied to a concave lens?
For a concave lens, the lens maker’s formula also considers the curvature of both surfaces and the refractive index. Concave lenses are thinner at the center and diverge light rays, making them appear to come from a focal point on the same side as the light source. The formula helps in designing concave lenses with the appropriate focal length for applications such as correcting myopia (nearsightedness).
What are the sign conventions used in the lens maker’s formula and why are they important?
The sign conventions in the lens maker’s formula are essential for consistent and accurate calculations. Typically, distances measured in the direction of the incoming light are positive, while those measured in the opposite direction are negative. For convex lenses, the focal length is positive, and for concave lenses, it is negative. Properly applying these conventions ensures correct determination of lens properties and behavior.
Why is understanding the lens maker’s formula crucial for lens design and manufacturing?
Understanding the lens maker’s formula is crucial for lens design and manufacturing because it allows precise control over the focal length and optical properties of the lens. This knowledge enables manufacturers to produce lenses that meet specific requirements for various optical devices, ensuring functionality and performance in applications such as vision correction, imaging, and scientific instruments.
How do the curvature and refractive index of a lens material influence its focal length according to the lens maker’s formula?
The curvature and refractive index of a lens material significantly influence its focal length. A lens with greater curvature (more pronounced bending of its surfaces) and a higher refractive index (ability to bend light) will have a shorter focal length, meaning it can converge or diverge light more strongly. Conversely, a lens with less curvature or a lower refractive index will have a longer focal length, providing a weaker converging or diverging effect. This relationship helps in designing lenses with specific focusing capabilities.