Lenz’s Law is named after the German physicist Heinrich Friedrich Emil Lenz, who formulated it in 1834. Lenz was not the first to notice the phenomenon of electromagnetic induction, but he was the first to provide a clear and concise rule for determining the direction of induced currents in conductors.
The early 19th century was a time of great discovery in the field of electromagnetism. In 1831, Michael Faraday discovered that a changing magnetic field could induce an electric current in a loop of wire—a phenomenon we now call Faraday’s Law of Induction. However, it was Lenz who, just a few years later, explained the direction of this induced current.
Lenz’s Law is fundamental to the operation of many modern technologies, such as electric generators, transformers, and induction motors. It’s a testament to the enduring power of scientific discovery that a principle formulated nearly two centuries ago continues to be applied in cutting-edge technologies today.
What is Lenz’s Law?
Lenz’s Law states that the direction of the induced current in a conductor will always be such that it opposes the change producing it.
In simpler terms, it implies that the induced current will create a magnetic field that opposes the change in the original magnetic field.
Lenz’s law is a principle that describes the direction of the induced current in a conductor by a changing magnetic field. It states that the induced current produces a magnetic field that opposes the change in magnetic flux that caused it. Lenz’s law is based on the conservation of energy and Newton’s third law.
Imagine you have a magic ring that doesn’t like change—whenever you try to bring a magnet close to it, the ring creates its magic to push the magnet away. This is similar to what happens in Lenz’s Law.
In physics terms, Lenz’s Law is all about how a conductor (like a coil of wire) reacts to changes in magnetic flux. When the magnetic environment around the conductor changes, it doesn’t just accept it; it fights back by creating its own current. This current is not random; it’s specifically in a direction that opposes the change that’s happening.
For example, if you move a magnet towards a coil, the coil will produce a current that creates a magnetic field to push the magnet away. If you pull the magnet away, the coil will generate a current that creates a magnetic field to pull the magnet back. It’s like the coil is saying, “Nope, I don’t want things to change!”
Lenz’s Law helps us understand how electric generators work, how to design safe circuits, and even how some of our everyday devices, like metal detectors, operate. When you think of Lenz’s Law, remember the magic ring that doesn’t like change. In simpler terms, if you try to change the magnetic environment of a coil or loop of wire, the coil will “fight back” by creating its own magnetic field that opposes your change.
Lenz’s Law Formula
When we talk about Lenz’s Law, we’re discussing the behavior of induced currents. The formula for Lenz’s Law is derived from Faraday’s Law of Electromagnetic Induction, which tells us how much voltage (or electromotive force) is induced in a loop when the magnetic flux through the loop changes.
The formula looks like this:
\(\displaystyle \text{Emf} = -N \left( \frac{\Delta \Phi}{\Delta t} \right) \)
- Emf stands for electromotive force.
- N is the number of turns or loops of wire you have. More loops mean more voltage!
- (∆Φ) represents the change in magnetic flux.
- (∆t) is the change in time.
Now, the most important part of this formula is the negative sign in front of it. This is where Lenz’s Law comes into play. The negative sign tells us that the induced voltage creates a current whose magnetic field opposes the change in flux. It’s nature’s way of saying, “I don’t like change, so I’m going to do something to resist it!”
Imagine you’re pushing a magnet toward a coil of wire. According to Lenz’s Law, the coil will generate a voltage that creates a current. This current then produces its own magnetic field that pushes back against the magnet you’re trying to move closer to. It’s like a cosmic tug-of-war!
The formula helps us predict not just the presence of this induced voltage but also its direction. It’s a beautiful example of how nature tends to resist changes and maintain balance.
Lenz’s Law Experiment
First experiment
Imagine you’re a scientist in the early 19th century, and you’re curious about this newfangled thing called electricity. You’ve heard about Faraday’s recent discovery that a changing magnetic field can induce an electric current, and you want to explore this further.
You have a coil of wire connected to a device that can detect current, called a galvanometer. You also have a bar magnet, which is going to be the source of your changing magnetic field. You decide to do something simple: move the magnet towards the coil and see what happens.
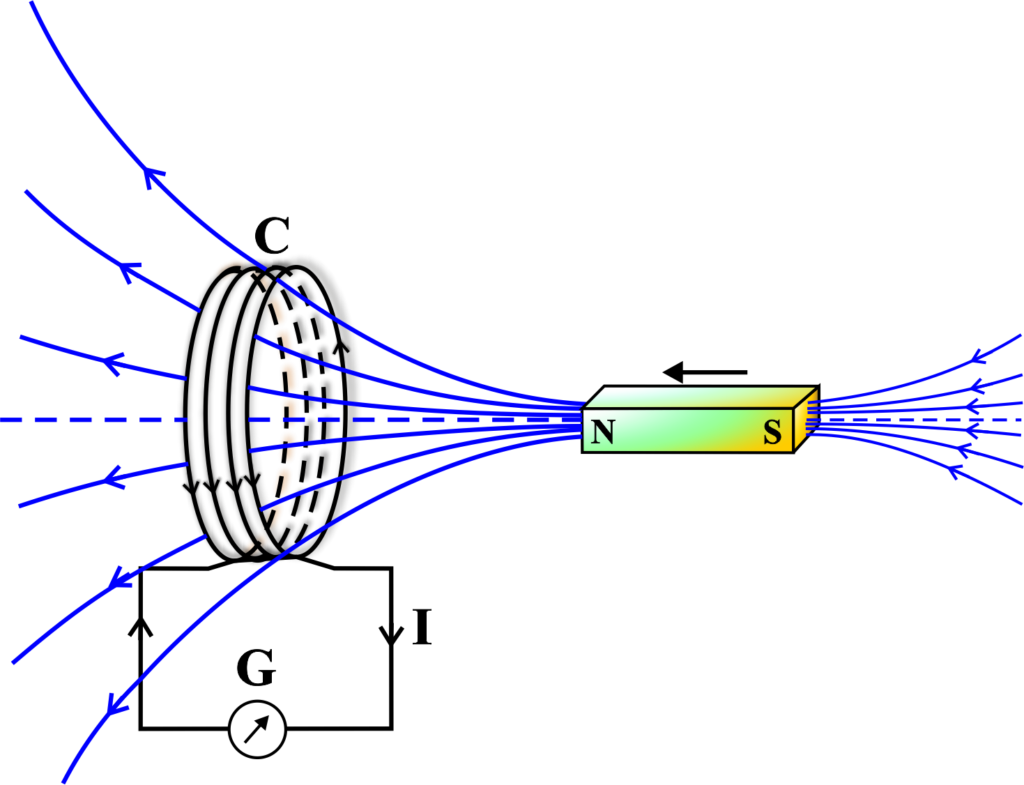
As the magnet gets closer, the magnetic field through the coil gets stronger. According to Faraday, this should induce a current in the coil.
As you move the magnet closer, the galvanometer needle swings! It indicates that a current is flowing through the coil. But which way is it flowing?
You remember that currents create magnetic fields, so this induced current must be creating its own magnetic field around the coil. The direction of the current is such that it creates a magnetic field that opposes the motion of the magnet.
Explanation:
Lenz said that the direction of the induced current would be such that it opposes the change in magnetic flux. In other words, the coil doesn’t like the magnet coming closer, so it creates a current that generates a magnetic field to push the magnet away. You try moving the magnet away from the coil, and the galvanometer needle swings the other way. This means the current is now flowing in the opposite direction, creating a magnetic field that tries to pull the magnet back.
According to Lenz’s Law, the induced current in the coil creates a magnetic field that opposes the motion of the approaching magnet. Thus, the north pole of the induced magnetic field will repel the north pole of the approaching magnet, causing the galvanometer to deflect in a certain direction.
Lenz’s first experiment showed that the induced current in a circuit will always flow in a direction that opposes the change in magnetic flux. This is a direct consequence of the conservation of energy. The coil is trying to keep the magnetic environment stable by “fighting” against the change.
So, in summary, Lenz’s first experiment is a perfect demonstration of his law in action, showing us that nature has a built-in preference for maintaining the status quo, at least when it comes to magnetic fields and electric currents.
Second experiment
Imagine you’re in a lab with two coils: Coil A and Coil B. Coil A is connected to a galvanometer, which is like a detective that can spot when an electric current is sneaking by. Coil B is connected to a battery, which gives it the power to create its own magnetic field.
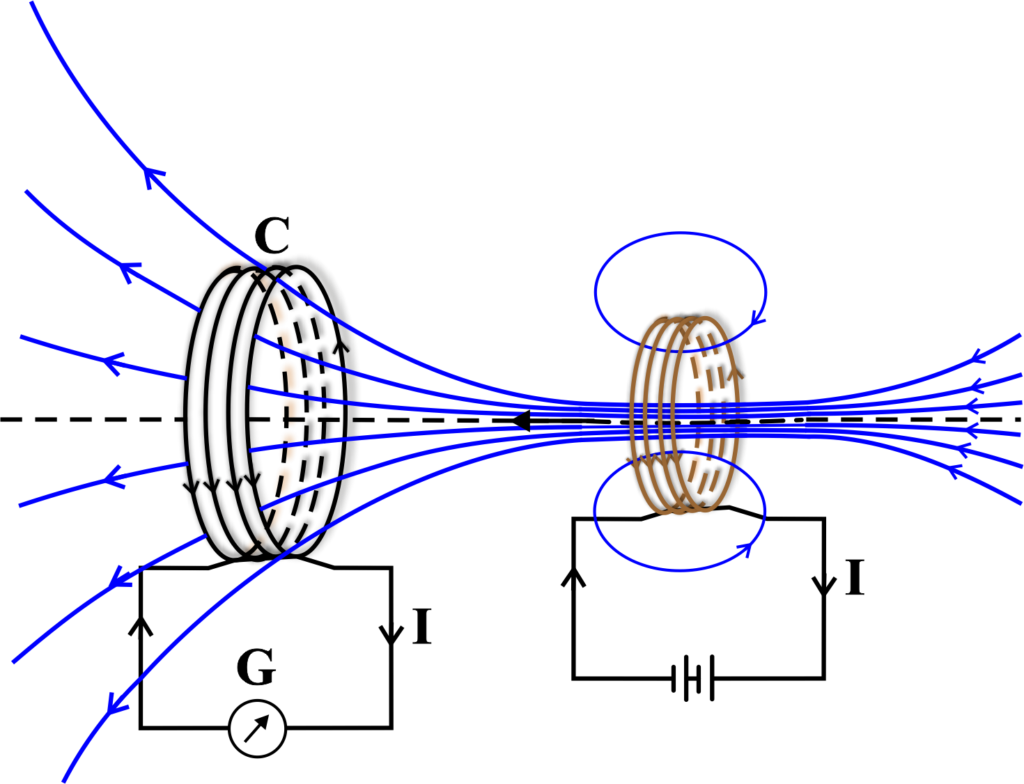
Coil B is moved towards Coil A, and then away from it. As it moves, it’s like Coil B is waving a magnet around Coil A, which changes the magnetic field that Coil A experiences.
When Coil B moves closer to Coil A, the galvanometer’s pointer swings one way. This tells us that a current has been induced in Coil A. But it’s not just any current; it’s a special one that follows Lenz’s Law.
The direction of this induced current in Coil A is such that it creates its own magnetic field. This new field is a superhero—it opposes the motion of Coil B. When Coil B moves towards Coil A, the induced field in Coil A acts like a repelling force, trying to push Coil B away.
Explanation: Now, when Coil B has moved away, the magnetic party it was throwing for Coil A starts to wind down—the magnetic flux through Coil A decreases. Lenz’s Law tells us that Coil A doesn’t like this; it wants the magnetic flux to stay the same. So, Coil A induces a current that creates a magnetic field to attract Coil B back, causing the galvanometer to swing the other way.
This experiment shows that Lenz’s Law is like nature’s way of saying, “I liked things the way they were!” It ensures that whenever there’s a change in the magnetic environment, the induced current will always act to keep things stable, opposing the change.
Third experiment
Picture yourself as an apprentice to a wizard who’s showing you how to control magical forces. In this case, the wizard is Lenz, and he’s demonstrating how a coil can resist changes in its magical realm, which is the magnetic field around it.
Lenz took a coil and moved it in and out of a magnetic field. This movement changed the amount of magnetic field—or ‘magical flux’—linking with the coil. When Lenz pulled the coil away from the magnetic field, the linked magnetic flux decreased. This is because the area of the coil inside the magnetic field got smaller. Lenz observed that as the coil was pulled out, an induced current was generated. But this wasn’t just any current; it was a current that opposed the motion of the coil being pulled out.
Explanation: According to Lenz’s Law, the induced current’s magnetic field opposed the decrease in magnetic flux. So, when the coil was pulled out, the induced current tried to create a magnetic field that would keep the coil inside the magnetic field.
This experiment shows that the coil, much like a stubborn character in a story, doesn’t want its ‘magical flux’ to change. When the coil is pulled out, it ‘fights back’ by inducing a current that tries to pull it back in. Lenz’s third experiment is a great example of how nature resists changes. It’s like a dance between the coil and the magnetic field, where the coil always moves to keep the magnetic field around it as stable as possible.
So, in summary, Lenz’s third experiment demonstrates that the induced current in a coil will always work to oppose the change in magnetic flux, whether that change is an increase or a decrease.
Lenz’s Law and Law of Conservation of Energy
Lenz’s Law is consistent with the Law of Conservation of Energy, which states that energy cannot be created or destroyed. The law ensures that the induced current does work to oppose the change in magnetic flux, maintaining energy balance.
Imagine you’re at a playground on a seesaw. You’re trying to balance it perfectly, but every time someone jumps on the other end, it tips. You have to push back to keep it level. This is similar to how Lenz’s Law works with the Law of Conservation of Energy.
Lenz’s Law tells us that when a change in magnetic flux induces a current, the direction of the induced current will be such that it opposes the change that caused it. The current is saying, “I don’t want things to change, so I’ll create a force to resist it!”
The Law of Conservation of Energy states that energy cannot be created or destroyed, only transformed from one form to another. When you move a magnet towards a coil, you’re using mechanical energy. According to Lenz’s Law, the coil resists this change by inducing a current that creates a magnetic field opposing the magnet’s motion.
Here’s where the two laws connect: The energy you use to move the magnet is transformed into electrical energy in the form of the induced current. The opposing magnetic field created by this current means you have to use more energy to keep moving the magnet. This extra effort ensures that the total energy (mechanical plus electrical) remains constant. The induced current does work against your push, which is consistent with the conservation of energy principle.
In essence, Lenz’s Law is nature’s way of enforcing the Law of Conservation of Energy in electromagnetic systems. It ensures that any energy put into changing the magnetic flux is balanced by the energy taken out in electrical resistance. So, just like you on the seesaw, Lenz’s Law keeps the universe’s energy balanced, making sure that everything adds up perfectly and nothing gets lost in the process.
Lenz’s Law Applications
Think of Lenz’s Law as a superhero power that can be used in many different gadgets and machines to make our lives easier. Here are some cool applications:
- Eddy Current Brakes: Imagine you’re on a roller coaster. To slow you down safely, the ride uses Lenz’s Law. When the coaster moves through a magnetic field, it induces currents in the metal of the coaster car. These currents create magnetic fields that oppose the motion, slowing the car down without any friction.
- Metal Detectors: These are like treasure hunters. They use Lenz’s Law to find hidden metal objects. When the detector’s magnetic field passes over a metal object, it changes the magnetic field in the coil of the detector. This change is detected and tells you there’s something buried there.
- Induction Cooktops: These cooktops use Lenz’s Law to heat up pots and pans without flames. They create a rapidly changing magnetic field that induces currents in the metal pot, which heats up due to the resistance of the metal.
- AC Generators: These are the powerhouses that keep our lights on. They convert mechanical energy into electrical energy using Lenz’s Law. As the generator spins, it changes the magnetic flux through the coils, inducing a current that we use as electricity.
- Card Readers: When you swipe your card at the store, Lenz’s Law is at work. The magnetic strip on your card changes the magnetic field in the reader, inducing a current that sends your card’s information to the computer.
- Microphones: Your voice can be turned into an electric signal thanks to Lenz’s Law. When you speak, the sound waves hit a diaphragm inside the microphone, moving it in a magnetic field and inducing a current that matches your voice.
These are just a few examples of how Lenz’s Law is used in technology. It’s amazing how a principle discovered in the 19th century is still so important in our modern world.
Lenz’s Law Limitations
Think of Lenz’s Law as a rule in a game that tells you how to react when something changes, but it doesn’t tell you everything about the game. Here are some limitations:
- Doesn’t Predict Magnitude: Lenz’s Law tells us the direction of the induced current, but it doesn’t say anything about how strong that current will be. It’s like knowing the direction to a friend’s house but not knowing how far away it is.
- Ideal Conditions Assumed: The law assumes ideal conditions without energy losses. In the real world, things like resistance and friction mean that the induced current can be less than what we might expect.
- Static Fields Only: Lenz’s Law applies to static magnetic fields. When dealing with changing magnetic fields, especially at high frequencies, things get more complicated, and additional factors come into play.
- Non-Conservative Forces: Lenz’s Law doesn’t take into account non-conservative forces like friction or air resistance, which can affect the motion of charged particles and the actual current produced.
- Quantitative Analysis: While Lenz’s Law is great for qualitative predictions about the direction of the current, it doesn’t provide a quantitative analysis. For that, you’d need to combine it with other laws and principles of electromagnetism.
Also Read: Faraday’s Laws of Electromagnetic Induction
Solved Examples
Problem 1: A rectangular loop of wire with dimensions (\(\displaystyle 0.5 \, \text{m} \times 0.3 \, \text{m} \)) is moved with a speed of (2 m/s) perpendicular to a uniform magnetic field of (0.2 T). Calculate the induced EMF and determine the direction of the induced current if the loop is part of a closed circuit.
Solution: Using the formula for induced EMF in a moving conductor:
\(\displaystyle \mathcal{E} = B \cdot l \cdot v \)
Given:
- Length (l = 0.5 m)
- Velocity (v = 2 m/s)
- Magnetic field (B = 0.2 T)
Calculate the induced EMF:
\(\displaystyle \mathcal{E} = 0.2 \cdot 0.5 \cdot 2 \)
\(\displaystyle \mathcal{E} = 0.2 \, \text{V} \)
The direction of the induced current can be determined using Lenz’s Law. The induced current will generate a magnetic field that opposes the motion of the loop. If the loop is moving to the right, the induced current will flow in such a way that it creates a magnetic field opposing the initial magnetic field, resulting in a counterclockwise current.
The induced EMF is (0.2 V), and the induced current flows counterclockwise.
Problem 2: A circular coil with 100 turns and a radius of (0.1 m) is placed in a magnetic field that increases uniformly from (0.5 T) to (1.5 T) in (0.2 s). Calculate the induced EMF in the coil.
Solution: Using Faraday’s Law:
\(\displaystyle \mathcal{E} = -N \frac{d\Phi}{dt} \)
Given:
- Number of turns (N = 100)
- Radius (r = 0.1 m)
- Initial magnetic field (Bi = 0.5 T)
- Final magnetic field (Bf = 1.5 T)
- Time interval (∆ t = 0.2 s)
Area of the coil:
\(\displaystyle A = \pi r^2 \)
\(\displaystyle A = \pi (0.1)^2 \)
\(\displaystyle A = 0.01\pi \, \text{m}^2 \)
Change in magnetic flux:
\(\displaystyle \Delta \Phi = A (B_f – B_i) \)
\(\displaystyle \Delta \Phi = 0.01\pi (1.5 – 0.5) \)
\(\displaystyle \Delta \Phi = 0.01\pi \cdot 1 \)
\(\displaystyle \Delta \Phi = 0.01\pi \, \text{Wb} \)
Average induced EMF:
\(\displaystyle \mathcal{E} = -N \frac{\Delta \Phi}{\Delta t} \)
\(\displaystyle \mathcal{E} = -100 \frac{0.01\pi}{0.2} \)
\(\displaystyle \mathcal{E} = -5\pi \)
\(\displaystyle \mathcal{E} \approx -15.7 \, \text{V} \)
The induced EMF in the coil is (-15.7 V).
Problem 3: A square loop of side (0.2 m) is rotating in a uniform magnetic field of (0.3 T). The plane of the loop is perpendicular to the magnetic field at (t = 0) and rotates with an angular velocity of (100rad/s). Determine the maximum induced EMF in the loop.
Solution: Using Faraday’s Law for a rotating loop:
\(\displaystyle \mathcal{E} = -N \cdot A \cdot B \cdot \omega \cdot \sin(\omega t) \)
Given:
- Side of the square loop (l = 0.2 m)
- Magnetic field (B = 0.3 T)
- Angular velocity (ω = 100 rad/s)
Area of the loop:
\(\displaystyle A = l^2 \)
\(\displaystyle A = (0.2)^2 \)
\(\displaystyle A = 0.04 \, \text{m}^2 \)
Maximum induced EMF occurs when (\(\displaystyle \sin(\omega t) = 1 \)):
\(\displaystyle \mathcal{E}{\text{max}} = A \cdot B \cdot \omega\)
\(\displaystyle \mathcal{E}{\text{max}} = 0.04 \cdot 0.3 \cdot 100 \)
\(\displaystyle \mathcal{E}_{\text{max}} = 1.2 \, \text{V} \)
The maximum induced EMF in the loop is (1.2 V).
Problem 4: A solenoid with 500 turns and a length of (0.5 m) has a cross-sectional area of (\(\displaystyle 0.02 \, \text{m}^2 \)). If the current through the solenoid changes uniformly from (2 A) to (5 A) in (0.1 s), calculate the induced EMF in the solenoid.
Solution: Using Faraday’s Law:
\(\displaystyle \mathcal{E} = -N \frac{d\Phi}{dt} \)
Magnetic flux in a solenoid:
\(\displaystyle \Phi = B \cdot A \)
\(\displaystyle B = \mu_0 \frac{N}{l} I \)
Given:
- Number of turns (N = 500)
- Length (l = 0.5 m)
- Cross-sectional area (A = 0.02 m2)
- Initial current (Ii = 2 A)
- Final current (If = 5 A)
- Time interval (∆ t = 0.1 s)
Change in magnetic flux:
\(\displaystyle \Delta \Phi = A \mu_0 \frac{N}{l} (I_f – I_i) \)
\(\displaystyle \Delta \Phi = 0.02 \cdot 4\pi \times 10^{-7} \cdot \frac{500}{0.5} (5 – 2) \)
\(\displaystyle \Delta \Phi = 0.02 \cdot 4\pi \times 10^{-7} \cdot 1000 \cdot 3 \)
\(\displaystyle \Delta \Phi = 0.02 \cdot 12\pi \times 10^{-4} \)
\(\displaystyle \Delta \Phi = 0.24\pi \times 10^{-4} \, \text{Wb} \)
Average induced EMF:
\(\displaystyle\mathcal{E} = -N \frac{\Delta \Phi}{\Delta t} \)
\(\displaystyle \mathcal{E} = -500 \frac{0.24\pi \times 10^{-4}}{0.1}\)
\(\displaystyle \mathcal{E} = -500 \cdot 2.4\pi \times 10^{-3} \)
\(\displaystyle\mathcal{E} = -1.2\pi \)
\(\displaystyle \mathcal{E} \approx -3.77 \, \text{V} \)
The induced EMF in the solenoid is (-3.77 V).
Problem 5: A rectangular coil with dimensions (\(\displaystyle 0.4 \, \text{m} \times 0.3 \, \text{m} \)) and 200 turns are placed in a magnetic field that changes from (0.3 T) to (1.2 T) in (0.3 s). Calculate the induced EMF in the coil.
Solution: Using Faraday’s Law:
\(\displaystyle \mathcal{E} = -N \frac{d\Phi}{dt} \)
Given:
- Number of turns (N = 200)
- Dimensions of the coil (l = 0.4 m) and (w = 0.3 m)
- Initial magnetic field (Bi = 0.3 T)
- Final magnetic field (Bf = 1.2 T)
- Time interval (∆ t = 0.3 s)
Area of the coil:
\(\displaystyle A = l \cdot w \)
\(\displaystyle A = 0.4 \cdot 0.3 \)
\(\displaystyle A = 0.12 \, \text{m}^2 \)
Change in magnetic flux:
\(\displaystyle \Delta \Phi = A (B_f – B_i) \)
\(\displaystyle \Delta \Phi = 0.12 (1.2 – 0.3) \)
\(\displaystyle \Delta \Phi = 0.12 \cdot 0.9 \)
\(\displaystyle \Delta \Phi = 0.108 \, \text{Wb} \)
Average induced EMF:
\(\displaystyle\mathcal{E} = -N \frac{\Delta \Phi}{\Delta t} \)
\(\displaystyle\mathcal{E} = -200 \frac{0.108}{0.3} \)
\(\displaystyle\mathcal{E} = -200 \cdot 0.36 \)
\(\displaystyle\mathcal{E} = -72 \, \text{V} \)
The induced EMF in the coil is (-72 V).
FAQs
What is Lenz’s Law in electromagnetism?
Lenz’s Law states that the direction of the induced electromotive force (emf) and the resulting current in a conductor will be such that it opposes the change in magnetic flux that caused the induction. This principle ensures that the induced current creates a magnetic field that opposes the original change in flux.
How does Lenz’s Law relate to the principle of conservation of energy?
Lenz’s Law is a manifestation of the conservation of energy. It ensures that the energy induced in the form of emf and current does not create energy from nothing but rather opposes the change in the magnetic field, thereby conserving energy within the system.
Can you provide a practical example illustrating Lenz’s Law?
A practical example of Lenz’s Law is the braking system in electric trains. When the brakes are applied, the change in magnetic flux induces currents that create an opposing magnetic field, generating a force that slows down the train.
What happens when a magnet is dropped through a copper tube, according to Lenz’s Law?
When a magnet is dropped through a copper tube, Lenz’s Law predicts that the falling magnet will induce currents in the copper tube. These currents will generate magnetic fields that oppose the motion of the magnet, causing it to fall more slowly than it would due to gravity alone.
How does Lenz’s Law explain the operation of induction cooktops?
In induction cooktops, alternating current flows through a coil beneath the cooking surface, creating a changing magnetic field. According to Lenz’s Law, this changing field induces currents in the metal cookware placed above the coil, which generates heat due to resistance, allowing cooking to occur.
What role does Lenz’s Law play in electric generators?
In electric generators, as the rotor turns and changes the magnetic flux through the coils, Lenz’s Law ensures that the induced currents create magnetic fields that oppose the motion of the rotor. This opposition requires mechanical work to maintain motion, effectively converting mechanical energy into electrical energy.
How is Lenz’s Law applied in electromagnetic damping?
Electromagnetic damping uses Lenz’s Law to slow down moving objects without physical contact. For instance, in certain measuring instruments, a conductive plate moving through a magnetic field experiences induced currents that generate opposing forces, reducing the motion smoothly and quickly.

well explained…!