The story of magnetism began over 2,500 years ago with the discovery of lodestones. These are naturally occurring magnets, found in the Magnesia region, hence the name ‘magnet’. Ancient Greeks, including the philosopher Thales of Miletus, observed that these stones could attract iron pieces.
During the Middle Ages, people began to understand more about magnetism. They discovered that a lodestone could magnetize a piece of iron, turning it into a magnet. This was the early foundation for the compass, which has been an essential tool for navigation.
In the 1600s, William Gilbert, an English physician, studied magnetism systematically and proposed that the Earth itself is a giant magnet. This was a revolutionary idea that changed the way people understood the world.
With the advent of the Industrial Revolution, there was a surge in the study of magnetic materials due to their practical applications. In the 19th century, scientists like Michael Faraday and James Clerk Maxwell laid the groundwork for our modern understanding of electromagnetism.
The 20th century saw significant advancements in the study of magnetic materials. In 1885, Carl W. von Siemens enhanced the magnetic properties of materials by heating them and then cooling them in a magnetic field. This led to the development of various types of magnetic materials, including soft and hard magnetic materials, which are crucial in modern technology for energy conversion in motors and generators.
Today, we continue to discover and innovate with magnetic materials. We’ve developed materials like ferrites and rare earth magnets, which have a wide range of applications from electronics to industrial machinery.
What is a Magnet?
A magnet is an object that produces a magnetic field, which is invisible but responsible for the most notable property of a magnet: a force that pulls on other ferromagnetic materials and attracts or repels other magnets.
Imagine you have a special stone that can pull towards certain metals like iron, nickel, or cobalt. This stone is not just any stone, but a magnet. Now, what makes this stone so special? It’s all about the invisible force field it creates around itself, known as the magnetic field. A magnet is an object that can exert a noticeable force on certain materials, even from a distance. This force can either attract or repel other magnets and can attract ferromagnetic materials like iron.
The magnetic field is the area around a magnet where magnetic forces can be felt. It’s invisible to the eye, but its effects are very real. If you’ve ever played with magnets, you’ve felt this force when you try to push two magnets together and they repel, or when they snap together because they attract.
Some magnets, like the ones on your fridge, are called permanent magnets. These are always magnetic and create their persistent magnetic field. Then there are temporary magnets. These are materials that act like magnets when they are within a magnetic field but lose their magnetism when the field is removed. An example would be an iron nail that becomes magnetic when near a strong magnet but loses its magnetism when taken away.
Lastly, we have electromagnets. These are made by coiling wire around an iron core and running an electric current through the wire. The electric current creates a magnetic field, which can be turned on and off with the current. This is how we can create large, powerful magnets that can be controlled.
The strength of a magnet is measured by its magnetization, which is the local strength of magnetism in a material. It’s like how much “magnetic power” the material has at any point. Every magnet has two ends, called poles. One is the North Pole, and the other is the South Pole. Opposite poles attract each other, while the same poles repel each other. This is why if you try to push the north poles of two magnets together, they will push away from each other.
If you break a magnet in half, you don’t get a north pole in one piece and a south pole in the other? Instead, you get two smaller magnets, each with its own north and south pole. So, a magnet is not just a stone or a piece of metal; it’s a fascinating object that interacts with the world in unique ways through its magnetic field. It’s like having a superpower to pull and push things without touching them!
What is a Magnetic Field?
A magnetic field is a vector field that describes the magnetic influence on moving electric charges, electric currents, and magnetic materials. A compass needle placed in a magnetic field will align itself along the field lines, showing the field’s direction.
Imagine you’re playing with two bar magnets. When you bring the ends close, you feel a force without any physical contact. This invisible force is due to the magnetic field.
A magnetic field is like a special effect area around magnets where they can exert their power. It’s not something you can see or touch, but you can see its effects. It’s what makes magnets stick to your fridge or causes compass needles to point north.
If you sprinkle iron filings around a magnet, they line up in a pattern. These patterns are called field lines and they show the direction of the magnetic field. They come out from the north pole of the magnet, curve around, and go into the south pole.
A magnetic field doesn’t just sit there; it does things. It can pull on some metals and push away others. If you put a compass in a magnetic field, the needle aligns with the field lines because the Earth itself is a giant magnet.
It’s not just magnets that create magnetic fields. When electricity flows through a wire, it creates a magnetic field around it. This is how electromagnets work. You can’t see the field, but you can see what it does, like picking up cars in a junkyard with a giant electromagnet.
The symbol for a magnetic field is usually a B or sometimes an H. Magnetic fields are super useful. They’re in electric motors, where they make things spin, and in generators, where they help produce electricity. They’re even in your phone and computer, helping to store data.
What is Magnetic Field Intensity?
Think of a group of fans cheering at a football game. The louder they cheer, the more intense the atmosphere. Now, imagine magnetic field intensity as the “loudness” of the magnetic field.
Magnetic field intensity, often symbolized as (H), is a measure of the strength of a magnetic field at a particular point. It’s like the volume knob on your music player; it controls how strong the magnetic field is. Magnetic field intensity is measured in units called amperes per meter (A/m). It’s a way of quantifying how much magnetic “oomph” there is in a given length of space.
Magnetic field intensity is important because it helps us understand how strong a magnet will be in different materials. Some materials need a higher “volume” of magnetism to show magnetic properties, while others need less.
In practical terms, engineers use magnetic field intensity to design and build things like MRI machines, which use strong magnetic fields to look inside your body, or electric motors, which use magnetic fields to turn electricity into motion.
Magnetic Properties of Materials
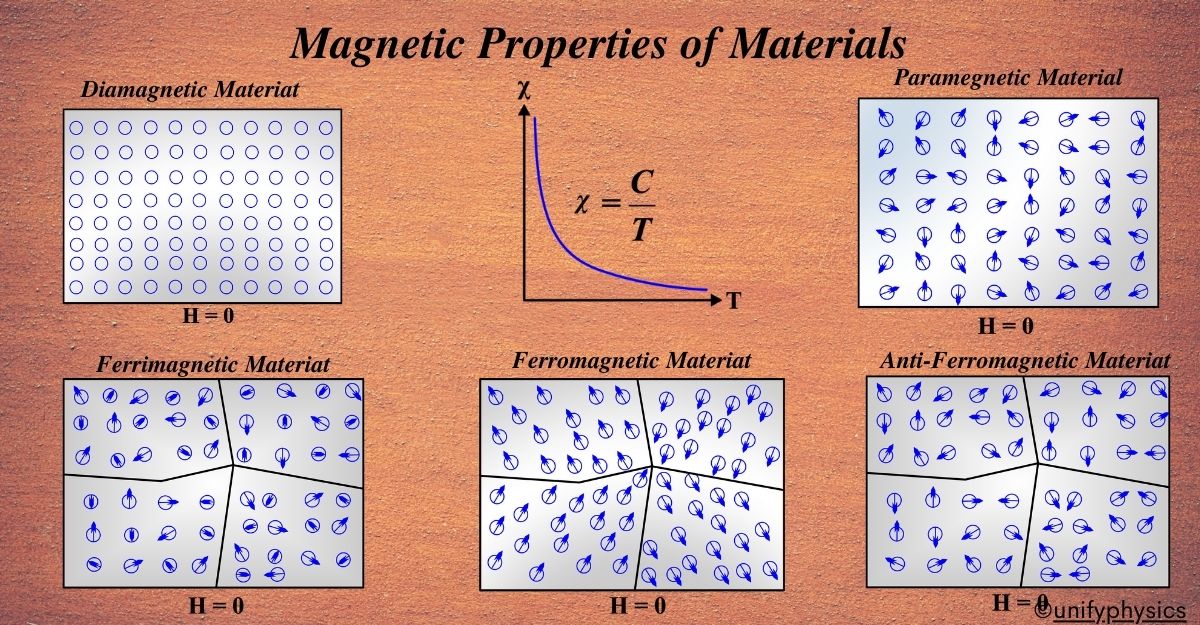
The study of magnetic properties encompasses various phenomena, including ferromagnetism, paramagnetism, diamagnetism, and antiferromagnetism, each characterized by distinct behaviors in the presence of an external magnetic field.
Diamagnetic Materials
Diamagnetic materials are those that produce a negative magnetization when placed in an external magnetic field. This means magnets repel them. This happens because the electrons in the atoms of these materials have paired spins, which cancel out each other’s magnetic moments.
In diamagnetic materials, the magnetic moments of individual atoms or molecules are randomly oriented, resulting in weak repulsion when exposed to an external magnetic field.

When an external magnetic field is applied, the electrons slightly change their orbits to oppose the field, creating a small induced magnetic moment in the opposite direction. This reduces the net magnetic field inside the material and causes a repulsive force.
The graph typically shows a weak negative susceptibility, indicating a slight decrease in magnetization with increasing magnetic field strength. At low fields, the magnetization may approach zero, but it doesn’t stay constant and may show a slight deviation from linearity as the field strength increases. Examples of diamagnetic materials are copper, silver, and water.
Paramagnetic Materials
Paramagnetic materials are those that acquire a small net magnetic moment in the direction of the applied field. This means the magnetic field slightly attracts them. This happens because the electrons in the atoms of these materials have some unpaired spins, which have non-zero magnetic moments.

When an external magnetic field is applied, these magnetic moments tend to align with the field, creating a small induced magnetic moment in the same direction. This increases the net magnetic field inside the material and causes an attractive force.
However, the alignment of the magnetic moments is not complete and is easily disturbed by thermal agitation. Therefore, the paramagnetism is weak and disappears when the external field is removed.

The graph shows a positive susceptibility, indicating an increase in magnetization with increasing magnetic field strength. However, the magnetization remains relatively weak compared to ferromagnetic materials. Examples of paramagnetic materials are aluminum, magnesium, and oxygen.
Curie’s law:
Curie’s law states that the magnetization of a paramagnetic material is directly proportional to the applied magnetic field and inversely proportional to the absolute temperature of the material.
This means that the magnetization increases with the magnetic field, but decreases with the temperature. The law can be expressed by the following formula:
\(\displaystyle M = C \frac{B}{T}\)
- M is the magnetization of the material, measured in ampere per meter (A/m) or emu/cm-3.
- C is the Curie constant, which depends on the material and its structure. It is measured in A m2/K or emu K/g.
- B is the magnetic field, measured in tesla (T) or gauss (G).
- T is the absolute temperature, measured in kelvin (K).
Curie’s law is valid for high temperatures and weak magnetic fields, where the thermal energy dominates over the magnetic interactions. At lower temperatures or higher magnetic fields, the law may not hold, and other effects such as saturation, hysteresis, or ferromagnetism may occur.
Curie’s law is useful for understanding the magnetic properties of paramagnetic materials, such as aluminum, magnesium, oxygen, and some transition metal compounds. It can also be used to measure the magnetic susceptibility, which is the ratio of the magnetization to the magnetic field, of these materials. The magnetic susceptibility is given by:
\(\displaystyle\chi = \frac{M}{B} = C \frac{1}{T}\)
The magnetic susceptibility is a dimensionless quantity that indicates how easily a material can be magnetized by an external field. It can be positive, negative, or zero depending on the type of material. For paramagnetic materials, the magnetic susceptibility is positive and small (about 10-3).
Ferromagnetic Materials
Ferromagnetic materials are those that are strongly attracted by the magnetic field. These materials retain the magnetism even when the magnetic field is removed.

This happens because the electrons in the atoms of these materials have many unpaired spins, which have large magnetic moments. These magnetic moments interact with each other and form small regions called domains, where all the magnetic moments are aligned in the same direction.
In the absence of an external magnetic field, the domains are randomly oriented, and the net magnetization of the material is zero.
When an external magnetic field is applied, the domains tend to align with the field, creating a large induced magnetic moment in the same direction. This greatly increases the net magnetic field inside the material and causes a strong attractive force.
The alignment of the domains is not easily disturbed by thermal agitation and persists even when the external field is removed. This is called the permanent magnetism or remanent magnetism of the material.
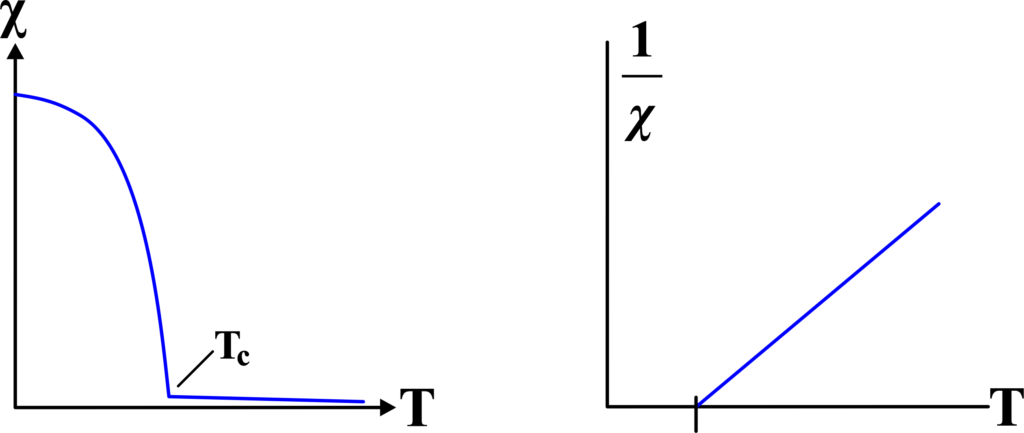
The graph shows a steep increase in magnetization with increasing magnetic field strength, often exhibiting hysteresis loops. At saturation, all domains are aligned, resulting in maximum magnetization. Examples of ferromagnetic materials are iron, nickel, and cobalt.
Curie Temperature:
The Curie temperature, named after the French physicist Pierre Curie, is a critical point for magnetic materials, especially ferromagnetic ones. Imagine a superhero who has the power of magnetism. They can attract metal objects and even fly by repelling the Earth’s magnetic field. But, when they get too hot, they lose their powers. The Curie temperature is like the temperature limit for ferromagnetic materials.
At the Curie temperature, ferromagnetic materials undergo a significant change. Below this temperature, they are strongly magnetic because their atomic magnetic moments are aligned. But once they reach the Curie temperature, they lose this alignment and their magnetic properties, becoming only weakly magnetic or paramagnetic.
The alignment of magnetic moments in ferromagnetic materials is disrupted by thermal energy. As the temperature rises, the atoms vibrate more vigorously, making it harder for the magnetic moments to stay aligned. At the Curie temperature, the thermal agitation is strong enough to overcome the magnetic forces keeping the moments in order.
The Curie temperature (Tc) is closely related to the Curie-Weiss Law, which describes the magnetic susceptibility (χ) of a material near the Curie temperature. The Curie-Weiss Law is given by the formula:
\(\displaystyle\chi = \frac{C}{T – T_c}\)
- (χ) is the magnetic susceptibility,
- (C) is the Curie constant,
- (T) is the absolute temperature,
- (Tc) is the Curie temperature.
This law helps predict the temperature at which a ferromagnetic material transitions to a paramagnetic state. It’s important to note that the Curie constant and the Curie temperature will vary depending on the material in question. The Curie temperature is a critical value specific to each ferromagnetic material and must be determined experimentally or from empirical data.
Ferromagnetic to Paramagnetic:
Imagine a superhero team where each member has a special magnetic power. When they work together, their powers combine to create a strong force. This is like the atoms in a ferromagnetic material, where the magnetic moments of the atoms are aligned, making the material act like a strong magnet.
In ferromagnetic materials, like iron, cobalt, and nickel, the magnetic moments of the atoms are all lined up in the same direction. This alignment happens within regions called domains. When these domains are aligned, the material is magnetized and exhibits strong magnetic properties.
As we learned earlier every ferromagnetic material has a special temperature known as the Curie temperature. At this temperature, something incredible happens: the superhero team starts to lose their unity. The thermal energy from the heat shakes things up, causing the atoms to move more and their magnetic moments to become disorganized.
As the temperature rises to the Curie point, the magnetic moments can no longer maintain their orderly arrangement. They start to point in random directions, and the material’s overall magnetism weakens significantly. This is the transition to the paramagnetic state, where the material only exhibits weak magnetism in the presence of an external magnetic field.
In the paramagnetic state, the material is like a disbanded superhero team. The members (atoms) are still there, but they’re not working together anymore. They only show a hint of their powers (magnetism) when a strong leader (external magnetic field) comes along to guide them.
Understanding this transition is important for many applications. For example, it helps in designing electrical components like transformers and hard drives, which need to maintain their magnetic properties under various temperature conditions.
So, the transition from ferromagnetic to paramagnetic states is like a team of superheroes losing their coordination as things heat up. It’s a fascinating phenomenon that shows how even the strongest magnetic materials can change under the right conditions!
Ferrimagnetic materials
Ferrimagnetic materials are those that have two sublattices of magnetic moments that are aligned in opposite directions but with unequal magnitudes. This results in a net magnetization that is nonzero, but weaker than that of ferromagnetic materials.
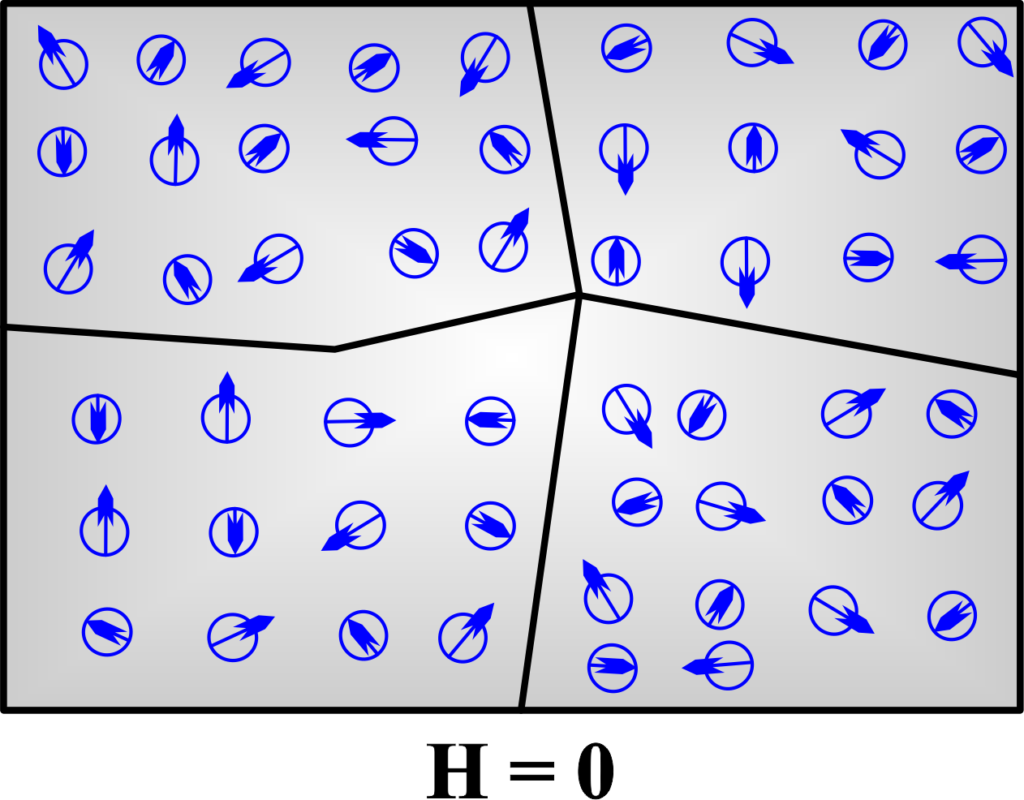
Ferrimagnetic materials are usually ceramic oxides that contain transition metal ions with different valences, such as Fe2+ and Fe3+.
The most common example of a ferrimagnetic material is magnetite (Fe3O4), which has one Fe2+ ion and two Fe3+ ions per unit cell.
The Fe2+ ion has a larger magnetic moment than the Fe3+ ions, and they are arranged in such a way that the two Fe3+ ions cancel each other out, while the Fe2+ ion contributes to the net magnetization.
Ferrimagnetic materials have high resistivity and anisotropic properties, meaning that their physical properties depend on the direction of the applied magnetic field. Ferrimagnetic materials have a Curie temperature above which they become paramagnetic and a compensation temperature below which they become antiferromagnetic.
The graph shows a positive susceptibility, but the magnetization may not reach saturation due to the presence of antiparallel magnetic sublattices. The hysteresis loop may exhibit a smaller area compared to ferromagnetic materials. Ferrimagnetic materials are used in various applications, such as data storage, sensors, and microwave devices.
Antiferromagnetic materials
Antiferromagnetic materials are those that have two sublattices of magnetic moments that are aligned in opposite directions, and with equal magnitudes. This results in a net magnetization that is zero, meaning that they do not produce any magnetic field of their own.
Antiferromagnetic materials are usually metals or alloys that contain atoms or ions with unpaired electrons, such as Mn, Cr, and FeO. The magnetic moments of these atoms or ions are influenced by the exchange interactions, which tend to align them in opposite directions to minimize the energy.
Antiferromagnetic materials have a Néel temperature above which they become paramagnetic and a critical field above which they become ferromagnetic.
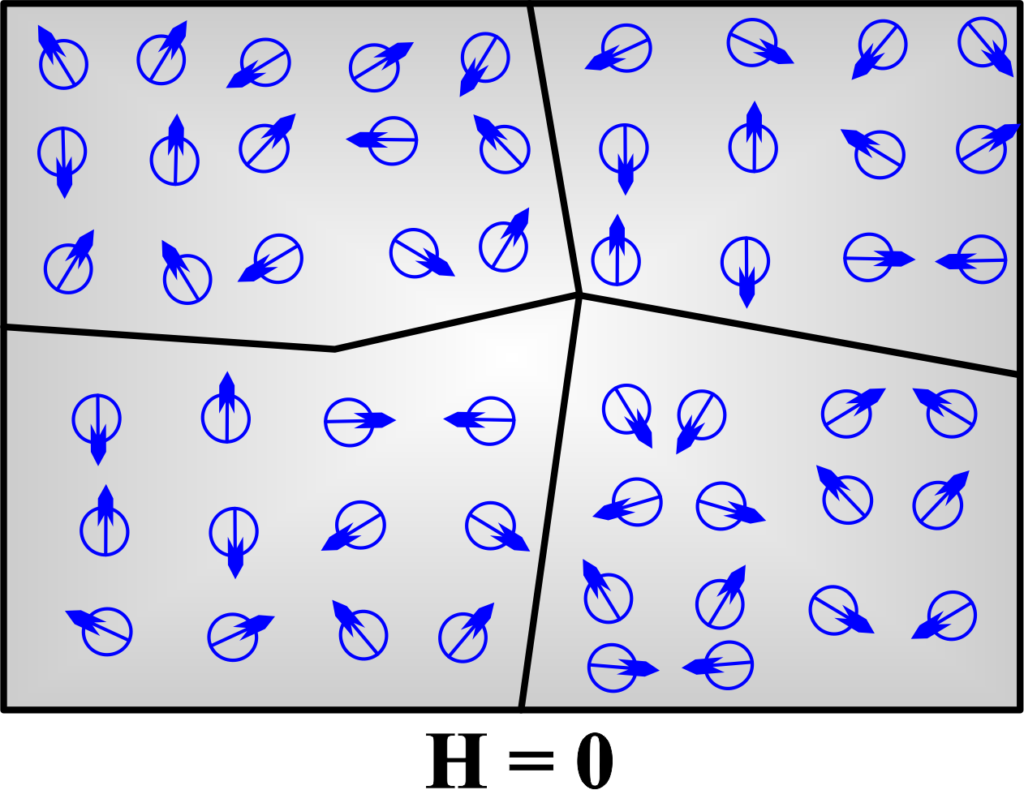
The graph typically shows a very small or negligible susceptibility, indicating minimal magnetization even in the presence of a strong magnetic field. The hysteresis loop may be absent or extremely small due to the cancellation of magnetic moments.
Antiferromagnetic materials are not affected by magnets, but they can exhibit some magnetic phenomena, such as spin canting, spin glass, and spin flop. Antiferromagnetic materials are used in various fields, such as spintronics, quantum computing, and magnetic resonance imaging.

Magnetic Properties of Matter
Magnetic field intensity (H)
Definition: Magnetic Field Intensity (H) is the measure of the magnetizing force exerted by an external source, such as a current-carrying wire or a magnet, in a region of space. It represents the strength of the magnetic field that induces magnetization in a material.
The relationship between Magnetic Field Intensity (H) and Magnetic Flux Density (B) is given by the equation:
\(\displaystyle B = \mu H\)
- (B) is the Magnetic Flux Density measured in teslas (T),
- (µ) is the permeability of the material (measured in henries per meter, H/m),
- (H) is the Magnetic Field Intensity.
The SI unit of Magnetic Field Intensity is amperes per meter (A/m). It can also be expressed in oersteds (Oe), but A/m is the standard unit used in the International System of Units (SI).
Intensity of magnetization (I)
The intensity of Magnetization, often denoted as I is a key concept in the study of magnetism, particularly in understanding how materials respond to magnetic fields.
The intensity of Magnetization (I) is defined as the magnetic moment per unit volume of a magnetized material. It represents the strength of magnetization within the material and indicates how much the material has been magnetized by an external magnetic field.
The formula for calculating the Intensity of Magnetization is:
\(\displaystyle I = \frac{M}{V} \)
- (I) is the Intensity of Magnetization,
- (M) is the total magnetic moment,
- (V) is the volume of the material.
The unit of Intensity of Magnetization is Ampere per meter (A/m), which shows the amount of magnetic moment in a given volume of material.
Magnetic susceptibility (χ)
Magnetic susceptibility (\chi_m$) is the ratio of the intensity of magnetization to the magnetic field intensity. It is a dimensionless quantity that indicates how easily a material can be magnetized. It can be positive, negative, or zero depending on the type of material. For diamagnetic materials, \(\displaystyle\chi_m\) is negative and very small (about 10-5). For paramagnetic materials, \(\displaystyle\chi_m\) is positive and small (about 10-3). For ferromagnetic materials, \(\displaystyle\chi_m\) is positive and large (about 103 to 106).
The intensity of magnetization (I) and magnetic susceptibility (χ) are closely related concepts in the study of magnetism.
Intensity of Magnetization is the measure of the magnetic moment per unit volume within a material. It indicates how much the material has been magnetized by an external magnetic field.
Magnetic Susceptibility is a dimensionless proportionality constant that indicates how easily a material can be magnetized within an external magnetic field. It’s a measure of the degree to which a material will become magnetized in response to an applied magnetic field.
The relationship between the intensity of magnetization (I) and magnetic susceptibility (χ) is given by the formula:
\(\displaystyle I = \chi H\)
- (I) is the intensity of magnetization,
- (χ) is the magnetic susceptibility,
- (H) is the magnetic field intensity.
This equation tells us that the intensity of magnetization in a material is directly proportional to the magnetic susceptibility and the magnetic field intensity. The higher the susceptibility, the more a material will become magnetized in the presence of a magnetic field.
So, magnetic susceptibility (χ) quantifies how responsive a material is to becoming magnetized, while the intensity of magnetization (I) is the result of that responsiveness when an external magnetic field (H) is applied. It’s a direct relationship where the susceptibility defines the level of magnetization that will occur for a given magnetic field intensity.
How does temperature affect magnetic susceptibility?
Temperature has a significant impact on the magnetic susceptibility of materials, and this effect varies depending on the type of material:
Paramagnetic Materials: For paramagnetic materials, magnetic susceptibility (χ) is inversely proportional to the absolute temperature (T). This relationship is described by Curie’s Law, which can be expressed as:
\(\displaystyle\chi = \frac{C}{T}\)
where (C) is the Curie constant, a characteristic property of the material. As the temperature increases, the thermal energy disrupts the alignment of atomic or molecular magnets within the material, leading to a decrease in magnetic susceptibility.
Diamagnetic Materials: Diamagnetic materials, on the other hand, have a negative magnetic susceptibility, and they are weakly repelled by an external magnetic field. Their magnetic susceptibility does not depend strongly on temperature and remains relatively constant across a range of temperatures.
Ferromagnetic Materials: For ferromagnetic materials, the relationship between magnetic susceptibility and temperature is more complex. At low temperatures, these materials exhibit spontaneous magnetization. However, as the temperature increases towards the Curie temperature, the thermal agitation becomes strong enough to disrupt the alignment of magnetic domains, causing a decrease in magnetic susceptibility. Above the Curie temperature, ferromagnetic materials transition to a paramagnetic state and follow Curie’s Law.
In simple terms, temperature can either weaken or maintain the magnetic susceptibility of materials, depending on their magnetic properties and the temperature range in question. This is a crucial factor to consider in applications where materials are exposed to varying thermal conditions.
Permeability (µ)
Permeability (\(\displaystyle\mu\)) is the measure of the resistance of a material against the formation of a magnetic field. It is expressed in units of Henry per meter (H/m) or gauss/oersted (G/Oe).
Permeability, denoted by the Greek letter µ, is a fundamental property in the field of electromagnetism that describes how a material responds to an applied magnetic field.
Permeability (µ) is the measure of the ability of a material to support the formation of a magnetic field within itself. In other words, it indicates how easily a magnetic field can penetrate and establish itself in a material.
The permeability of a material is related to the magnetic flux density (B) and the magnetic field intensity (H) through the formula:
\(\displaystyle\mu = \frac{B}{H}\)
- (µ) is the permeability,
- (B) is the magnetic flux density, measured in teslas (T),
- (H) is the magnetic field intensity, measured in amperes per meter (A/m).
The permeability of free space (µ0) is a constant value of \(\displaystyle 4\pi \times 10^{-7}\) H/m. The permeability of a material (µm) is related to the permeability of free space and the magnetic susceptibility by the equation
\(\displaystyle\mu_m = \mu_0 (1 + \chi_m)\).
The SI unit of permeability is henries per meter (H/m) or newtons per ampere squared (N/A²). This unit reflects how much inductance is produced per unit length of the material when a magnetic field is applied.
Retentivity
Think of retentivity as the ability of a material to remember its magnetic experiences. It’s like when you learn something new and remember it even after the class is over.
Retentivity, also known as residual magnetism, is the measure of how much magnetization remains in a material after an external magnetic field is removed. It’s a key property of ferromagnetic materials that determines their ability to serve as permanent magnets.
The retentivity of a material is often represented by the symbol (Br) and is part of the hysteresis loop of a magnetic material. While there isn’t a simple formula for retentivity, it is related to the coercive force (Hc) and the material’s permeability.
The retentivity can be visualized on a graph where the magnetic field strength (H) is plotted against the magnetic flux density (B). The point on the graph where (H = 0) and ( B ) is not zero represents the retentivity. The unit of retentivity is the same as magnetic flux density, which is Tesla (T) in the International System of Units (SI). It tells us the level of residual magnetism in a material.
Key Points:
- Retentivity is the ability of a material to retain or resist magnetization after the removal of the external magnetic field.
- It depends on the hysteresis curve of the material, which is a plot of the magnetic flux density (B) versus the magnetic field intensity (H) for a complete cycle of magnetization and demagnetization.
- The retentivity is the value of the magnetic flux density when the magnetic field intensity is zero after the material has been magnetized to saturation. It is also called the residual magnetism or the remanence.
- The retentivity is high for ferromagnetic materials, meaning they can retain a large amount of magnetization even without an external field.
- For diamagnetic and paramagnetic materials, the retentivity is zero, meaning they lose all their magnetization when the external field is removed.
So, retentivity is like the magnetic version of memory. It’s what makes some materials great for making permanent magnets, like the ones you stick on your fridge, because they can “remember” the magnetization long after the magnetizing force is gone!
Coercivity
Coercivity is the intensity of the external magnetic field that must be applied to a magnetized material to reduce its magnetization to zero. In other words, it’s the force required to overcome the material’s own magnetism. It is also called the coercive force or the coercive field.
The coercivity is high for ferromagnetic materials, meaning they require a large amount of external field to be demagnetized. For diamagnetic and paramagnetic materials, the coercivity is zero, meaning they can be easily demagnetized by a small external field.
Imagine a strong person who can resist being pushed around. Coercivity is like that person’s strength but for magnets. It’s the measure of a ferromagnetic material’s resistance to becoming demagnetized.
The unit of coercivity is oersted (Oe) in the centimeter-gram-second (CGS) system or ampere per meter (A/m) in the International System of Units (SI). It’s a measure of the magnetic field strength needed to demagnetize the material.
Coercivity tells us how “tough” a magnetic material is. High coercivity means the material can stay magnetized even in the presence of other magnetic fields, which is great for making permanent magnets. It’s an important property for designing magnetic storage media, electric motors, and any technology that relies on stable magnetic fields.
Other Properties
Properties of Magnetic Field Lines
Magnetic field lines are a visual tool we use to represent the invisible magnetic field around magnets.
- Directional Flow: The direction of the magnetic field is tangent to the field line at any point. This means if you place a compass in the field, it will align with the field lines, showing the direction of the magnetic field.
- Field Strength: The closeness or density of the field lines indicates the strength of the magnetic field. Where the lines are closer together, the field is stronger; where they’re spread out, it’s weaker.
- Never Cross: Magnetic field lines never intersect. If they did, it would mean there are two directions of the magnetic field at one point, which is impossible.
- Closed Loops: They form continuous, closed loops from the north pole to the south pole of a magnet. Inside the magnet, they continue from the south pole back to the north pole.
- Polar Concentration: The magnetic field is strongest at the poles of a magnet, where the field lines are most concentrated.
- Vector Nature: Magnetic field lines have both direction and magnitude, making them vector fields. This means they not only show the direction of the magnetic field but also its relative strength.
Remember, these lines are a conceptual tool to help us understand and visualize magnetic fields; they don’t exist but are incredibly useful for explaining and predicting magnetic behavior.
Magnetic Moments
Magnetic moments are a fundamental concept in physics that describe the strength and direction of a magnet’s influence. Imagine a tiny compass needle inside every atom. This needle is the atom’s magnetic moment, and it determines how the atom will behave in a magnetic field.
The magnetic moment is a vector quantity that represents the magnetic strength and orientation of a magnet or any object that produces a magnetic field. It’s the property that dictates how a magnet will interact with external magnetic fields.
For a simple bar magnet or a loop of wire carrying a current, the magnetic moment (m) can be calculated using the formula:
\(\displaystyle m = NIA\)
For a magnet, the magnetic moment is related to the torque (τ) it experiences in a magnetic field (B) by the formula:
\(\displaystyle\tau = m \times B\)
The unit of the magnetic moment is Ampere-square meters (Am²), which shows the product of the current and the area for a current-carrying loop. It can also be expressed in terms of torque and magnetic field strength, resulting in the unit Joules per Tesla (J/T).
Understanding magnetic moments is crucial for explaining why magnets behave the way they do, from sticking to your fridge to powering electric motors. It’s the magnetic “personality” of an object that defines its interaction with the magnetic world around it!
Magnetic Flux Density
Magnetic Flux Density, often denoted as B, is a key concept in electromagnetism that describes how strong a magnetic field is in a given area.
Magnetic Flux Density (B) is the amount of magnetic flux through a unit area taken perpendicular to the direction of the magnetic field. It tells us how concentrated the magnetic field is in a specific region.
The magnetic flux density is calculated using the formula:
\(\displaystyle B = \frac{\Phi}{A}\)
The unit of Magnetic Flux Density is the Tesla (T). One Tesla is equivalent to one Weber per square meter, where a Weber is the unit of magnetic flux.
In simpler terms, if you imagine the magnetic field as a crowd of people walking through a door, the magnetic flux density would tell you how many people are passing through the door per second. A higher number means a stronger magnetic field in that area.
Effect of Temperature on Magnetization
Temperature can significantly affect a material’s magnetization. As temperature increases, thermal energy can cause the aligned magnetic moments to become disordered, decreasing the material’s overall magnetization.
Imagine a group of dancers who are perfectly synchronized. This is similar to the magnetic domains in a magnet, which are aligned to create a strong magnetic field. Now, what happens when the temperature changes?
- Heating Up: As the temperature increases, the atoms in the magnet start moving more vigorously. This is like the dancers starting to move faster and faster, making it harder for them to stay in sync. The increased thermal energy can cause the magnetic moments of the atoms to become disoriented, leading to a decrease in the magnet’s overall strength.
- The Curie Point: There’s a specific temperature for each ferromagnetic material called the Curie Temperature. At this point, the thermal agitation is so intense that it completely disrupts the alignment of the magnetic domains. The material loses its ferromagnetic properties and becomes paramagnetic, which means it only magnetizes weakly in the presence of an external magnetic field.
The Curie-Weiss Law provides a formula that relates the magnetic susceptibility of a material to its temperature in relation to the Curie point. The law is given by:
\(\displaystyle\chi = \frac{C}{T – T_c}\)
This formula applies to paramagnetic materials above their Curie temperature. It shows that the magnetic susceptibility decreases as the temperature increases beyond the Curie point. The Curie-Weiss Law is a modification of Curie’s Law, which states that the magnetic susceptibility of a paramagnetic material is inversely proportional to its temperature and is given by:
\(\displaystyle \chi = \frac{C}{T}\)
However, the Curie-Weiss Law accounts for the presence of the Curie temperature and provides a more accurate description near the Curie point. It’s important to note that these laws are applicable in the paramagnetic phase, above the Curie temperature, where the material no longer exhibits ferromagnetism.
- Cooling Down: Lower temperatures generally enhance a magnet’s performance. Just like dancers might perform better in cooler conditions, the magnetic moments in a material can align more easily when the thermal energy is lower.
- Extreme Cold: At very low temperatures, some materials can become superconductors and exhibit perfect diamagnetism, repelling magnetic fields entirely.
So, temperature can either weaken or strengthen the magnetization of materials, depending on whether it’s increased or decreased.
Also Read: Hysteresis
Solved Examples
Problem 1: A long cylindrical rod of ferromagnetic material has a magnetization (M = 800A/m). If the relative permeability of the material is (µr = 1000), calculate the magnetic field (B) inside the rod.
Solution: The magnetic field (B) inside a material is given by:
\(\displaystyle B = \mu_0 \mu_r H \)
The relationship between (H) and (M) is given by:
\(\displaystyle H = \frac{M}{\mu_r – 1} \)
Given: M = 800 A/m; µr = 1000
Calculate (H):
\(\displaystyle H = \frac{800}{1000 – 1} \)
\(\displaystyle H \approx \frac{800}{999} \)
\(\displaystyle H \approx 0.8008 \, \text{A/m} \)
Now calculate (B):
\(\displaystyle B = \mu_0 \mu_r H \)
\(\displaystyle B = (4\pi \times 10^{-7}) \times 1000 \times 0.8008 \)
\(\displaystyle B \approx 4\pi \times 10^{-4} \times 0.8008 \)
\(\displaystyle B \approx 1.005 \times 10^{-3} \, \text{T} \)
The magnetic field (B) inside the rod is approximately (\(\displaystyle 1.005 \times 10^{-3} \, \text{T} \)).
Problem 2: The magnetization (M) of a paramagnetic material is (150 A/m) when subjected to a magnetic field (H = 1000 A/m). Calculate the magnetic susceptibility (χm) of the material.
Solution: Magnetic susceptibility (χm) is given by:
\(\displaystyle \chi_m = \frac{M}{H} \)
Given: M = 150 A/m; H = 1000 A/m.
Calculate (χm):
\(\displaystyle \chi_m = \frac{150}{1000} \)
\(\displaystyle \chi_m = 0.15 \)
The magnetic susceptibility (χm) of the material is ( 0.15 ).
Problem 3: A solenoid of length (0.5 m) and (1000) turns carries a current of (2 A). The solenoid has a ferromagnetic core with a relative permeability (µr = 500). Calculate the magnetic field (B) inside the solenoid.
Solution: The magnetic field (B) inside a solenoid with a core is given by:
\(\displaystyle B = \mu_0 \mu_r n I \)
Given: Length of the solenoid ( l = 0.5 m); Total number of turns (N = 1000); Current (I = 2 A)
Number of turns per unit length (n):
\(\displaystyle n = \frac{N}{l} = \frac{1000}{0.5} = 2000 \, \text{turns/m} \)
Calculate (B):
\(\displaystyle B = (4\pi \times 10^{-7}) \times 500 \times 2000 \times 2 \)
\(\displaystyle B = 4\pi \times 10^{-7} \times 1000 \times 4000 \)
\(\displaystyle B = 4\pi \times 10^{-3} \times 4 \)
\(\displaystyle B \approx 0.016 \pi \, \text{T} \)
\(\displaystyle B \approx 0.05024 \, \text{T} \)
The magnetic field (B) inside the solenoid is approximately (0.05024 T).
Problem 4: A ferromagnetic material has a magnetic field (B = 0.02 T) and a magnetic intensity (H = 100 A/m). Calculate the magnetization (M) of the material.
Solution: The magnetic field (B) is related to the magnetization (M) and magnetic intensity (H) by:
\(\displaystyle B = \mu_0 (H + M) \)
Given: B = 0.02 T; H = 100 A/m
Rearrange to solve for (M):
\(\displaystyle 0.02 = 4\pi \times 10^{-7} (100 + M) \)
\(\displaystyle 0.02 = 4\pi \times 10^{-5} (100 + M) \)
\(\displaystyle 0.02 = 1.25664 \times 10^{-4} (100 + M) \)
\(\displaystyle 0.02 / 1.25664 \times 10^{-4} = 100 + M \)
\(\displaystyle 159.15 \approx 100 + M \)
\(\displaystyle M \approx 59.15 \, \text{A/m} \)
The magnetization (M) of the material is approximately (59.15 A/m).
Problem 5: Calculate the energy density (u) of the magnetic field in a region where the magnetic field (B = 0.1 T).
Solution: The energy density (u) of a magnetic field is given by:
\(\displaystyle u = \frac{B^2}{2\mu_0} \)
Given: B = 0.1 T.
Calculate (u):
\(\displaystyle u = \frac{(0.1)^2}{2 \times 4\pi \times 10^{-7}} \)
\(\displaystyle u = \frac{0.01}{8\pi \times 10^{-7}} \)
\(\displaystyle u = \frac{0.01}{2.51327 \times 10^{-6}} \)
\(\displaystyle u \approx 3978.87 \, \text{J/m}^3 \)
The energy density (u) of the magnetic field is approximately (\(\displaystyle 3978.87 \, \text{J/m}^3\) ).
FAQs
What are the main types of magnetic materials?
The main types of magnetic materials are ferromagnetic, paramagnetic, diamagnetic, and antiferromagnetic. Each type exhibits different magnetic behaviors in the presence of an external magnetic field.
What is ferromagnetism and which materials exhibit this property?
Ferromagnetism is the phenomenon where certain materials, such as iron, cobalt, and nickel, exhibit strong, permanent magnetism. These materials have magnetic domains that align in the presence of an external magnetic field, and they retain their magnetization even after the external field is removed.
How do paramagnetic materials respond to an external magnetic field?
Paramagnetic materials, like aluminum and platinum, have a weak and temporary positive response to an external magnetic field. Their magnetic moments align with the field, but the alignment is weak and disappears once the field is removed.
What characterizes diamagnetic materials?
Diamagnetic materials, such as copper and bismuth, create an induced magnetic field in a direction opposite to an externally applied magnetic field, causing a weak repulsion. This effect is present in all materials but is often masked by stronger magnetic properties in other types of materials.
What is antiferromagnetism?
Antiferromagnetism is a type of magnetic ordering where adjacent ions or atoms have magnetic moments that are aligned in opposite directions, canceling each other out. This results in no net macroscopic magnetization. Examples include manganese oxide (MnO) and iron oxide (FeO).
How does temperature influence the magnetic properties of materials?
Temperature significantly affects magnetic properties. For ferromagnetic materials, increasing temperature can reduce their magnetization. At a critical temperature called the Curie temperature, they lose their ferromagnetic properties and become paramagnetic. For antiferromagnetic materials, a similar transition occurs at the Néel temperature.
What are soft and hard magnetic materials?
Soft magnetic materials, like iron and silicon steel, are easily magnetized and demagnetized. They have low coercivity and are used in applications like transformers and inductors. Hard magnetic materials, such as neodymium magnets and samarium-cobalt magnets, retain their magnetization and have high coercivity. They are used in permanent magnets and magnetic storage devices.