The earliest known magnets were naturally occurring minerals called lodestones, which are pieces of the mineral magnetite that have been magnetized. These were discovered by ancient civilizations such as the Greeks, who named them after the region of Magnesia where they were found.
The first major application of magnetism was the magnetic compass, which the Chinese invented during the Han dynasty (around 206 BCE to 220 CE). This device was crucial for navigation at sea and significantly contributed to the Age of Exploration.
During the Middle Ages, European scholars began to study magnetism systematically. One of the most notable figures was Petrus Peregrinus, who wrote the letter “Epistola de magnete” in 1269, which discussed the properties of magnets and the Earth’s magnetism.
The Renaissance period saw further developments, with scientists like William Gilbert, who published “De Magnete” in 1600. Gilbert proposed that the Earth itself was a giant magnet and introduced the term “magnetic pole.”
The 19th century was a pivotal time for magnetism. Hans Christian Ørsted discovered that electric currents create magnetic fields, which led to the development of electromagnetism by André-Marie Ampère and Michael Faraday.
James Clerk Maxwell unified electricity and magnetism into a single theory with his famous Maxwell’s Equations, which were published between 1861 and 1862. These equations describe how electric and magnetic fields are generated and altered by each other and by charges and currents.
In the 20th century, scientists like Pierre Curie studied the magnetic properties of materials at the atomic level, leading to quantum mechanical explanations of magnetism. Today, magnetism is a cornerstone of modern technology, finding applications in everything from electric motors to data storage.
What is Magnetism?
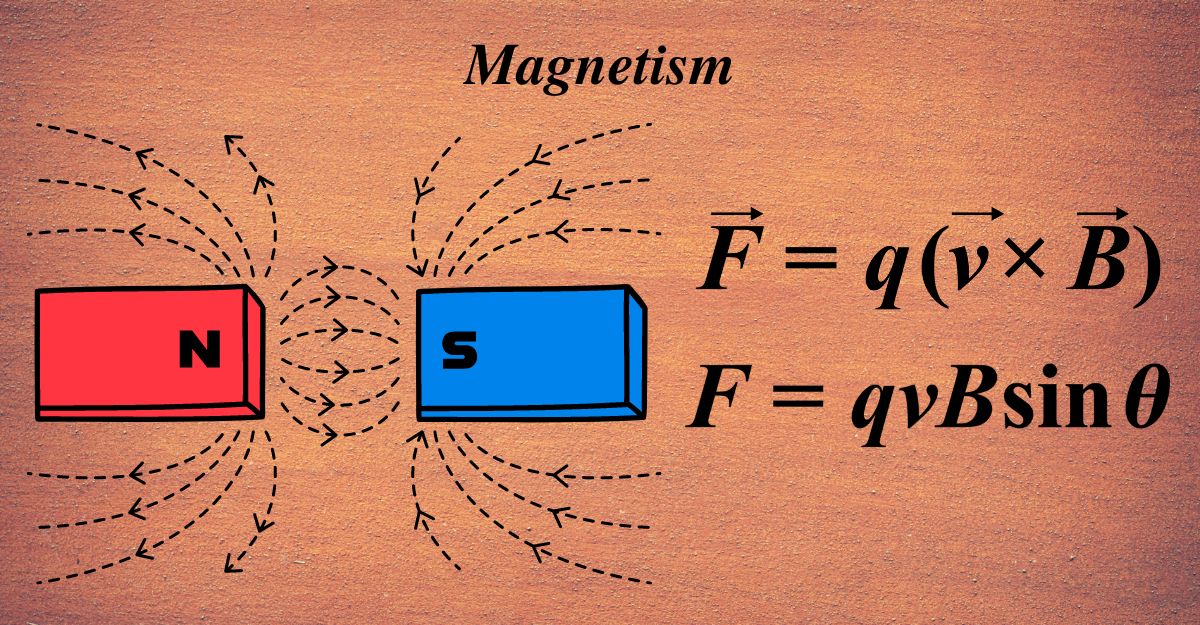
Magnetism is a force that can attract or repel certain materials, such as iron, nickel, and cobalt. The motion of electric charges causes it. Imagine you have two bar magnets. Each one has a north pole and a south pole. If you try to bring the same poles together, they repel each other, but opposite poles attract. This invisible force of attraction or repulsion is what we call magnetism.
At its core, magnetism is caused by electric charges in motion. In most materials, electrons spin in random directions, and their magnetic effects cancel each other out. However, in magnetic materials, these spins tend to align in the same direction, which creates a net magnetic field.
This magnetic field is what exerts the magnetic force on other materials and is responsible for the interaction between magnets. The field is strongest at the poles of the magnet and can be visualized using magnetic field lines, which emanate from the north pole and curve around to enter the south pole.
The Earth itself acts like a giant magnet with a magnetic field extending far into space, which is why compasses always point north. This geomagnetic field is also what shields us from harmful solar radiation.
In the modern world, magnetism is not just about magnets attracting iron. It’s a critical component of many technologies. For instance, when electric current flows through a wire, it creates a magnetic field around it. This principle is used in everything from electric motors to MRI machines in hospitals.
The Magnetism of Earth
Earth itself is a giant magnet with a magnetic field extending into space. This field protects us from solar winds and is responsible for phenomena like the auroras. Imagine the Earth as a giant magnet. This isn’t just a metaphor; it’s quite literal. The Earth generates a vast magnetic field, which we call the geomagnetic field.
Deep within the Earth’s core, there’s a churning sea of molten iron and nickel. These metals are not only magnetic but also in constant motion due to the Earth’s rotation and convection currents. This movement of liquid metal generates electric currents, which in turn create the Earth’s magnetic field.
The Earth’s magnetic field has a North Pole and a South Pole, much like the bar magnets you’re familiar with. However, these aren’t aligned perfectly with the geographic poles. In fact, the magnetic poles wander and can even flip over geological timescales.
This geomagnetic field extends far into space and acts like a shield, protecting us from solar winds and cosmic radiation. Without it, life on Earth would be exposed to much more ionizing radiation, which could have severe consequences for living organisms.
For centuries, navigators have used compasses to find their way. A compass works because its magnetic needle is influenced by the Earth’s magnetic field, always pointing towards the magnetic North Pole.
It’s interesting to note that a compass doesn’t point to the true North (geographic North) but to the magnetic North. The angle between the direction a compass needle points and true North is known as magnetic declination.
Over the Earth’s history, the direction of the magnetic field has flipped many times. Although we don’t fully understand why or how quickly these reversals happen, we know they’re a normal part of the Earth’s magnetic behavior.
Magnetism Properties
Magnets have two poles, north and south, where the magnetic force is strongest. Opposite poles attract, while like poles repel each other. We see this in detail in the following section,
- Poles: Every magnet has two poles: a North Pole and a South Pole. These are the points where the magnet’s force is strongest. When suspended freely, magnets will align themselves with the Earth’s magnetic field, which is why a compass needle points North.
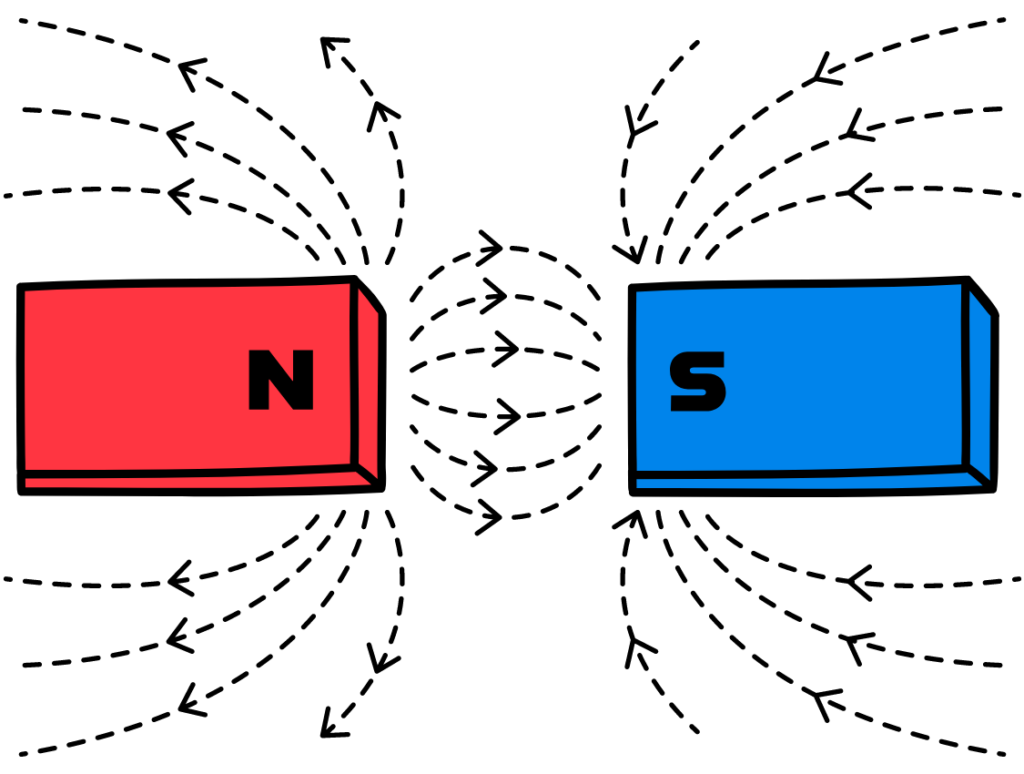
- Attraction and Repulsion: Magnets exhibit a force that can either attract or repel other magnets. Like poles repel each other (North repels North, South repels South), while opposite poles attract (North attracts South, and vice versa).
- Inseparable Poles: If you cut a magnet in half, you don’t get a single North or South pole; each piece will still have both a North and a South Pole. This is different from electric charges, where you can have a positive or negative charge in isolation.
- Magnetic Field: This is the area around a magnet where its magnetic force is effective. It’s invisible to the eye but can be represented visually with the help of iron filings or a magnetic field viewer.
- Magnetic Dipole: A magnet can be thought of as having a magnetic dipole, with a North and South Pole creating a magnetic loop. The strength of this dipole is called the magnetic dipole moment, and it’s a vector quantity pointing from the South to the North Pole.
- Magnetic Field Lines: These are imaginary lines used to represent the magnetic field. They emerge from the North Pole and enter the South Pole. The density of these lines indicates the strength of the magnetic field: closer lines mean a stronger field.
Magnetism Types
Diamagnetism
Diamagnetism is a type of magnetism that is present in all materials but is usually overshadowed by stronger forms of magnetism in certain materials. Diamagnetism is a fundamental property of all matter, although it’s very weak in comparison to other types of magnetism. It arises from the response of electron orbits to an external magnetic field. In diamagnetic materials, all the electrons are paired, and their spins cancel out, leading to no net magnetic moment in the absence of an external field.
When a diamagnetic material is placed in a magnetic field, it creates an induced magnetic field in the opposite direction. This is because the electrons adjust their orbits slightly to oppose the applied field. As a result of this induced field, diamagnetic materials are repelled by a magnetic field. The effect is weak and can only be observed with strong magnets or very sensitive instruments.
Unlike other types of magnetism, diamagnetism is not affected by changes in temperature. The diamagnetic response remains constant regardless of how hot or cold the material gets. Common examples of diamagnetic materials include water, wood, gold, copper, and bismuth. These materials do not retain magnetization when the external field is removed.
While not often used for their magnetic properties due to the weak effect, diamagnetism has interesting applications in areas like magnetic levitation, where objects can be made to float stably above a strong magnetic field. In essence, diamagnetism is a subtle but universal form of magnetism that results from the intrinsic properties of electrons in atoms.
Paramagnetism
Paramagnetism is a form of magnetism where certain materials are weakly attracted by an externally applied magnetic field. Unlike ferromagnetic materials, which are strongly attracted, or diamagnetic materials, which are repelled, paramagnetic materials have a much weaker attraction to magnetic fields.
The key feature of paramagnetic materials is that they have atoms with unpaired electrons. These unpaired electrons give the material a small net magnetic moment, which is aligned with the external magnetic field.
When a paramagnetic material is placed in a magnetic field, the unpaired electrons’ magnetic moments tend to align with the field, causing a weak attraction. This alignment is temporary and disappears when the external field is removed.
Paramagnetism is influenced by temperature. According to Curie’s Law, the magnetization of a paramagnetic material is inversely proportional to its temperature. As the temperature increases, the thermal energy causes the magnetic moments to become disoriented, decreasing the material’s magnetization.
Paramagnetic materials have a positive magnetic susceptibility, which means they are weakly attracted to magnetic fields. However, this susceptibility is small compared to ferromagnetic materials.
Examples of paramagnetic materials include aluminum, platinum, and some transition metal complexes. These materials do not retain magnetization in the absence of a magnetic field. Paramagnetic materials are used in various applications, such as in magnetic resonance imaging (MRI) as contrast agents to enhance the quality of the image.
Paramagnetism is a type of magnetism characterized by a weak attraction to magnetic fields, primarily due to the presence of unpaired electrons in the material’s atoms. It’s a subtle but important property that has practical applications in technology and medicine.
Curie’s Law: Curie’s Law was formulated by the French physicist Pierre Curie. The law states that the magnetization (M) of a paramagnetic material is directly proportional to the applied magnetic field (B). However, this magnetization is inversely proportional to the temperature (T) of the material.
Mathematically, Curie’s Law can be expressed as:
\(\displaystyle M = \frac{C \times B}{T} \)
- (M) is the magnetization of the material,
- (B) is the applied magnetic field (measured in Tesla),
- (T) is the absolute temperature (measured in Kelvins),
- (C) is the Curie constant, which is specific to the material.
This relationship implies that as the temperature of a paramagnetic material increases, its ability to become magnetized decreases. Conversely, if the temperature remains constant, an increase in the magnetic field will increase the material’s magnetization.
There’s also a related concept known as the Curie temperature, which is the temperature at which a ferromagnetic material becomes paramagnetic. This transition is significant in various applications, including data storage technologies.
Ferromagnetism
Ferromagnetism is the phenomenon where certain materials, like iron, cobalt, nickel, and gadolinium, can be strongly magnetized. This is the type of magnetism you see in everyday magnets stuck on a fridge door.
In ferromagnetic materials, there are regions called magnetic domains. Each domain is like a tiny magnet with its own north and south poles. In an unmagnetized state, these domains are randomly oriented, but they can align in the presence of a magnetic field, causing the material to become magnetized.
What’s special about ferromagnetic materials is that they can retain their magnetization even after the external magnetic field is removed. This is how permanent magnets are created.
Ferromagnetic materials have a specific temperature, known as the Curie temperature, above which they lose their ferromagnetic properties and become paramagnetic. This is because the thermal energy at higher temperatures disrupts the alignment of the magnetic domains.
Ferromagnetism isn’t just a cool science fact; it’s incredibly useful. These materials are used in transformers, electromagnets, and magnetic storage media, like hard drives.
Curie Temperature:
The Curie Temperature, named after the French physicist Pierre Curie, is the temperature at which a ferromagnetic material loses its permanent magnetic properties and becomes paramagnetic. The Curie Temperature is a key concept in the study of magnetism, particularly for materials known as ferromagnets, which include common metals like iron, nickel, and cobalt.
Ferromagnetism to Paramagnetism: At temperatures below the Curie Temperature, ferromagnetic materials have domains where the magnetic moments of atoms are aligned, giving the material a strong, permanent magnetism. When heated to the Curie Temperature, these materials undergo a phase transition, and the thermal energy causes the magnetic moments to become disordered. As a result, the material’s overall magnetism disappears, and it behaves like a paramagnet, only magnetizing in the presence of an external magnetic field and not retaining magnetism afterward.
This law describes the magnetic susceptibility of paramagnetic materials above the Curie Temperature. It shows that the susceptibility is inversely proportional to the difference between the absolute temperature and the Curie Temperature.
The Curie-Weiss Law can be mathematically expressed as:
\(\displaystyle \chi = \frac{C}{T – T_C} \)
- (χ) is the magnetic susceptibility,
- (C) is the Curie constant (specific to the material),
- (T) is the absolute temperature,
- (TC) is the Curie Temperature.
The Curie Temperature marks the point at which a material’s intrinsic magnetic order is disrupted by thermal energy, leading to a change in its magnetic properties.
Anti-Ferromagnetism
Anti-ferromagnetism is a type of magnetism where the magnetic moments within a material spontaneously align in opposite directions, resulting in no net magnetization. This alignment is temperature-dependent and changes when the material is heated beyond the Neel temperature.
In anti-ferromagnetic materials, the atoms or ions have a permanent magnetic moment, usually due to unpaired electron spins, similar to what you find in ferromagnetic and paramagnetic materials.
What’s unique about anti-ferromagnetic materials is the way these magnetic moments are arranged. Instead of all lining up in the same direction, they align in alternating opposite directions within a domain. This means that for every north magnetic pole, there’s a south magnetic pole next to it, and vice versa.
Because the magnetic moments are aligned in opposite directions, they cancel each other out. This results in the material having no net magnetization or susceptibility under normal conditions.
Anti-ferromagnetic materials have a critical temperature known as the Neel temperature, named after Louis Neel who discovered this phenomenon. Below this temperature, the anti-parallel alignment of magnetic moments is stable. Above the Neel temperature, the material transitions to a paramagnetic state, where the magnetic moments are no longer aligned in any particular order.
As the temperature increases, the domain structure that supports anti-ferromagnetism breaks down, and the material becomes paramagnetic. However, unlike ferromagnetic materials, which experience a dramatic decrease in susceptibility with rising temperature, anti-ferromagnetic materials start with zero susceptibility and show an increase in susceptibility as they transition to the paramagnetic state.
Ferrimagnetism
Ferrimagnetism is a type of permanent magnetism where the magnetic moments within a material are aligned in both parallel and antiparallel directions, resulting in net magnetization. Ferrimagnetic materials have atoms with magnetic moments, similar to ferromagnetic materials. However, in ferrimagnetism, these moments are not all aligned in the same direction.
In ferrimagnetic materials, the magnetic moments of atoms or ions spontaneously align in a pattern that is both parallel and antiparallel. This means some moments point in one direction and others in the opposite, but unlike antiferromagnetism, these moments are not equal in magnitude.
Because the magnetic moments are unequal, they don’t cancel each other out completely. This results in a net magnetization for the material, which is why ferrimagnetic materials can be considered magnets.
These materials are typically found in magnetic oxides known as ferrites. A common example is magnetite, a natural magnet that has been known since ancient times. Like other magnetic materials, ferrimagnetism is temperature-dependent. There is a specific temperature, known as the Curie temperature, below which the material exhibits ferrimagnetism. Above this temperature, the material becomes paramagnetic.
Ferrimagnetic materials are used in various applications, including transformers, inductors, and magnetic recording media, due to their favorable magnetic properties.
Magnetic Materials
(i) Diamagnetic Materials:
Diamagnetic materials are substances that are repelled by both poles of a magnet. Unlike ferromagnetic materials, which are strongly attracted to magnets, diamagnetic materials exhibit a very weak form of magnetism.
In diamagnetic materials, all the electrons are paired, and each pair of electrons has opposite spins. This means that the magnetic fields of the electrons cancel each other out, resulting in no net magnetic moment within the atom.
When an external magnetic field is applied to a diamagnetic material, it induces a very weak magnetic field in the opposite direction. This is due to Lenz’s Law, which states that the direction of the induced current (and thus the induced magnetic field) will be such that it opposes the change in the magnetic field that produced it.
Properties of Diamagnetic Materials:
- Repulsion: They are weakly repelled by a magnetic field.
- Magnetic Susceptibility: They have a negative magnetic susceptibility, meaning they are repelled by magnetic fields.
- Temperature Independent: Their diamagnetic properties do not change with temperature.
- Permeability: The relative permeability of diamagnetic materials is slightly less than one.
If you place a diamagnetic material in a non-uniform magnetic field, it will move from the stronger part to the weaker part of the field. This is because the induced magnetization is in the opposite direction to the applied field, causing a repulsive force. Common examples include materials like water, wood, gold, copper, and bismuth.
While the diamagnetic effect is weak, it’s still important in applications like magnetic levitation, where diamagnetic materials can be levitated in a strong magnetic field due to their repulsion from the field.
So, diamagnetic materials are those that exhibit a weak, negative response to a magnetic field due to their unique electron configuration. This property makes them stand out from other magnetic materials and has interesting applications in the field of physics and engineering.
(ii) Paramagnetic Material:
Paramagnetic materials are weakly attracted to magnets due to their unpaired electrons. Their magnetism is temporary and influenced by temperature.
Paramagnetic materials are those that are weakly attracted to a magnetic field. Unlike diamagnetic materials, which are repelled, or ferromagnetic materials, which are strongly attracted, paramagnetic materials fall somewhere in between.
The key to paramagnetism lies in the electrons. Paramagnetic materials have atoms with at least one unpaired electron. Since electrons are tiny magnets themselves, these unpaired electrons give the material a magnetic moment.
When you place a paramagnetic material in a magnetic field, the unpaired electrons’ magnetic moments will align with the field, causing a weak attraction. This alignment is temporary; remove the field, and the material stops being magnetic.
Paramagnetism is temperature-dependent. According to Curie’s Law, the magnetization of a paramagnetic material is inversely proportional to its temperature. As the temperature increases, the thermal energy causes the magnetic moments to become disoriented, decreasing the material’s magnetization.
This is a measure of how much a material will become magnetized in an applied magnetic field. For paramagnetic materials, this value is small and positive, indicating weak attraction.
Some examples of paramagnetic materials include aluminum, calcium, and certain transition metal complexes. These materials do not retain magnetization in the absence of a magnetic field.
(iii) Ferromagnetic Materials:
Ferromagnetic materials are substances that can be strongly magnetized and are typically what we think of as “magnets”. They can retain their magnetic properties even after the external magnetic field is removed.
These materials are strongly attracted to magnets and can become permanent magnets themselves. Inside ferromagnetic materials, there are regions called magnetic domains. Each domain is like a tiny magnet with a North and South Pole. In an unmagnetized state, these domains are randomly oriented. However, when exposed to a magnetic field, they can align in the same direction, causing the material to become magnetized.
There’s a specific temperature for each ferromagnetic material, known as the Curie temperature, above which it loses its ferromagnetic properties. This is because the thermal energy at higher temperatures disrupts the alignment of the magnetic domains. Common examples of ferromagnetic materials include iron, cobalt, nickel, and some of their alloys. Gadolinium and certain rare earth materials also exhibit ferromagnetism.
Due to their strong magnetic properties, ferromagnetic materials are used in various applications such as in the cores of transformers, in the manufacturing of various types of magnets, and data storage devices like hard drives.
Some ferromagnetic materials can become permanent magnets. This happens when their domains remain aligned even after the external magnetic field is removed. The process of making a permanent magnet involves placing the material in a strong magnetic field and then heating it to a certain temperature (below its Curie temperature) before cooling it down.
So, ferromagnetic materials are those that not only respond strongly to magnetic fields but can also retain their magnetism, making them essential in both everyday applications and advanced technologies.
Magnetic Force
Magnetic force is the force exerted by a magnetic field on a moving charge, a current-carrying wire, or another magnet. It’s one of the primary forces that we encounter in electromagnetism.
If you place a magnet near a magnetic material or another magnet, you’ll notice that they either attract or repel each other. This is due to the magnetic force. The same force is at play when an electric current flows through a wire and experiences a force in a magnetic field.
The direction of the magnetic force on a moving charge is always perpendicular to both the velocity of the charge and the magnetic field. This is famously described by the right-hand rule: if you point your thumb in the direction of the charge’s velocity and your index finger in the direction of the magnetic field, your middle finger will point in the direction of the force.
The magnitude of the magnetic force (F) on a moving charge (q) with velocity (v) in a magnetic field (B) is given by the equation:
\(\displaystyle F = qvB \sin(\theta) \)
where (θ) is the angle between the velocity and the magnetic field vectors. The magnetic force on a moving charge in a magnetic field is given by the Lorentz force law. The force is perpendicular to both the velocity of the charge and the magnetic field.
Consider a charged particle with charge (q) moving with a velocity (\(\displaystyle \vec{v} \)) in a magnetic field represented by ( \(\displaystyle\vec{B} \)).
The magnetic part of the Lorentz force law states that the magnetic force (\(\displaystyle\vec{F}\)) on a moving charge is proportional to the charge (q), the velocity (\(\displaystyle\vec{v}\)), and the magnetic field (\(\displaystyle\vec{B}\)), and it depends on the sine of the angle (θ) between the velocity and the magnetic field vectors.
The force is given by the cross-product of the velocity and the magnetic field:
\(\displaystyle \vec{F} = q(\vec{v} \times \vec{B}) \)
The magnitude of this force can be calculated using the formula for the cross-product:
\(\displaystyle F = qvB\sin(\theta) \)
- (F) is the magnitude of the force,
- (q) is the charge of the particle,
- (v) is the magnitude of the velocity,
- (B) is the magnitude of the magnetic field,
- (θ) is the angle between the velocity and the magnetic field.
The direction of the force is perpendicular to both (\(\displaystyle \vec{v}\)) and (\(\displaystyle \vec{B}\)), and it follows the right-hand rule. If you point your thumb in the direction of (\(\displaystyle\vec{v}\)) and your index finger in the direction of (\(\displaystyle\vec{B}\)), your middle finger will point in the direction of (\(\displaystyle\vec{F}\)).
When a current-carrying wire is placed in a magnetic field, each moving charge within the wire experiences a magnetic force.A wire carrying a current (I), the force on a small segment of the wire (\(\displaystyle d\vec{l} \)) in a magnetic field is given by:
\(\displaystyle d\vec{F} = I(d\vec{l} \times \vec{B}) \)
For the entire wire, we integrate along its length to find the total force:
\(\displaystyle \vec{F} = I \int (d\vec{l} \times \vec{B}) \)
This derivation shows how the magnetic force depends on the charge, its velocity, and the magnetic field. It’s a fundamental concept that explains how charges interact with magnetic fields and forms the basis for understanding how electric motors, generators, and many other devices work. Remember, the actual force experienced by a charge also depends on the electric field present, but for this derivation, we’re focusing solely on the magnetic component of the Lorentz force.
Uses of Magnets
Magnets are not just objects sticking to your refrigerator door; they are at the heart of many devices and technologies that shape our modern world.
- Electronics: Magnets are integral to the functioning of hard drives, where they store data. Speakers and microphones also rely on magnets to convert electrical energy into sound and vice versa.
- Electric Motors and Generators: In these devices, magnets are essential for converting electrical energy into mechanical energy (motors) or mechanical energy into electrical energy (generators).
- Medical Technology: Magnets play a crucial role in MRI machines, which use strong magnetic fields to create detailed images of the body’s interior. They are also explored for their potential in cancer treatment.
- Industrial Machinery: Magnets are used in heavy lifting equipment, such as cranes, to move large metal objects. They also help in separating metallic ores from rocks during mining operations.
- Daily Life: At home, magnets are used in various ways, from fridge magnets to hold notes to magnetic bottle openers. Even the simple compass relies on Earth’s magnetic field to point north.
- Transportation: Some trains, known as maglev trains, use magnets to levitate above the tracks, reducing friction and allowing for higher speeds.
- Payment Cards: The strips on the back of credit and debit cards are magnetic, storing your account information just like a computer’s hard drive.
Understanding these applications helps students appreciate the practical importance of magnets and encourages them to think innovatively about how magnetism can be harnessed in future technologies. Magnets are a clear example of how a simple physical phenomenon can have wide-ranging and profound applications.
Also Read: Biot-Savart Law
Solved Examples
Problem 1: A material exhibits diamagnetic behavior and has a magnetic susceptibility (χm) of (\(\displaystyle -4.5 \times 10^{-6}\)). If the material is placed in a magnetic field of 0.5 T, calculate the magnetization (M) of the material.
Solution: For diamagnetic materials, the magnetization (M) is given by:
\(\displaystyle M = \chi_m \cdot H \)
First, we need to convert the magnetic field (B) into the magnetic field intensity (H) using the relation:
\(\displaystyle B = \mu_0 H \)
where (\(\displaystyle\mu_0 = 4\pi \times 10^{-7} \, \text{T}\cdot\text{m}/\text{A}\)) (permeability of free space).
\(\displaystyle H = \frac{B}{\mu_0} = \frac{0.5 \, \text{T}}{4\pi \times 10^{-7} \, \text{T}\cdot\text{m}/\text{A}} \)
\(\displaystyle H = \frac{0.5}{4\pi \times 10^{-7}} \)
\(\displaystyle H \approx 3.98 \times 10^5 \, \text{A/m} \)
Now, calculate the magnetization (M):
\(\displaystyle M = \chi_m \cdot H \)
\(\displaystyle M = -4.5 \times 10^{-6} \times 3.98 \times 10^5 \)
\(\displaystyle M \approx -1.79 \, \text{A/m} \)
The magnetization of the diamagnetic material is (-1.79 A/m).
Problem 2: A paramagnetic material has a Curie constant (C) of (\(\displaystyle 1.2 \times 10^{-2} \, \text{K}\cdot\text{m}/\text{A}\)). At a temperature of 300 K and in a magnetic field of 0.2 T, find the magnetic susceptibility (χm) of the material.
Solution: According to Curie’s law, the magnetic susceptibility (χm) is given by:
\(\displaystyle \chi_m = \frac{C}{T} \)
where (T) is the temperature in Kelvin.
\(\displaystyle \chi_m = \frac{1.2 \times 10^{-2}}{300} \)
\(\displaystyle \chi_m = 4 \times 10^{-5} \)
The magnetic susceptibility of the paramagnetic material is (4 × 10-5).
Problem 3: A ferromagnetic material has a hysteresis loop with an area of (50 J/m3). If this material is subjected to an alternating magnetic field with a frequency of 60 Hz, calculate the power loss due to hysteresis.
Solution: The power loss due to hysteresis (P) in a ferromagnetic material is given by:
\(\displaystyle P = \text{area of hysteresis loop} \times \text{frequency} \)
\(\displaystyle P = 50 \, \text{J/m}^3 \times 60 \, \text{Hz} \)
\(\displaystyle P = 3000 \, \text{W/m}^3 \)
The power loss due to hysteresis is (3000 W/m3).
Problem 4: An antiferromagnetic material has a Neel temperature (TN) of 250 K. If the temperature of the material is increased to 300 K, describe the behavior of its magnetic susceptibility.
Solution: For antiferromagnetic materials, the magnetic susceptibility (χm) decreases as the temperature is raised above the Neel temperature (TN). Below (TN), the susceptibility increases with temperature. However, above (TN), the material behaves more like a paramagnetic material, and (χm) follows Curie’s law.
Since the temperature 300 K is above the Neel temperature of 250 K, the material’s magnetic susceptibility will decrease compared to its value at (TN) and will follow a paramagnetic behavior.
Above the Neel temperature, the magnetic susceptibility of the antiferromagnetic material will decrease and behave like a paramagnetic material.
Problem 5: A ferrimagnetic material has two sublattices with magnetizations (M1) and (M2) where (\(\displaystyle M_1 = 2 \times 10^6 \, \text{A/m}\)) and (\(\displaystyle M_2 = 1 \times 10^6 \, \text{A/m}\)) respectively, and they are aligned oppositely. Calculate the net magnetization of the material.
Solution: The net magnetization (Mnet) in a ferrimagnetic material is the vector sum of the magnetizations of the two sublattices. Since they are aligned oppositely, we subtract one from the other:
\(\displaystyle M_{\text{net}} = M_1 – M_2 \)
\(\displaystyle M_{\text{net}} = 2 \times 10^6 \, \text{A/m} – 1 \times 10^6 \, \text{A/m} \)
\(\displaystyle M_{\text{net}} = 1 \times 10^6 \, \text{A/m} \)
The net magnetization of the ferrimagnetic material is (1 × 106 A/m).
Problem 6: A proton is moving with a velocity of (3 × 105 m/s) perpendicular to a magnetic field of strength 0.8 T. Calculate the magnetic force acting on the proton.
Solution: The magnetic force (F) on a moving charge is given by:
\(\displaystyle F = q v B \sin \theta \)
where (q) is the charge of the proton (\(\displaystyle 1.6 \times 10^{-19} \, \text{C}\)), (v) is the velocity, (B) is the magnetic field strength, and (θ) is the angle between the velocity and the magnetic field (which is 90 degrees or (\(\displaystyle\pi/2\)) radians in this case).
\(\displaystyle F = (1.6 \times 10^{-19} \, \text{C}) \times (3 \times 10^5 \, \text{m/s}) \times (0.8 \, \text{T}) \times \sin(90^\circ) \)
\(\displaystyle F = (1.6 \times 10^{-19}) \times (3 \times 10^5) \times 0.8 \)
\(\displaystyle F = 3.84 \times 10^{-14} \, \text{N} \)
The magnetic force acting on the proton is (3.84 × 10-14 N).
FAQs
What is the origin of magnetism in materials?
Magnetism in materials originates from the motion of electrons. Specifically, it is due to the electrons’ spin and their orbital motion around the nucleus. In certain materials, these magnetic moments align in a specific way, creating a net magnetic field.
How do magnetic domains contribute to the overall magnetism of a material?
Magnetic domains are small regions within a material where the magnetic moments of atoms are aligned in the same direction. When these domains are aligned uniformly, the material exhibits strong magnetism. However, in an unmagnetized material, the domains are oriented randomly, canceling each other out and resulting in no net magnetic field.
What is the difference between a permanent magnet and an electromagnet?
A permanent magnet maintains its magnetic properties without an external power source, due to the alignment of its magnetic domains. An electromagnet, on the other hand, is made of a coil of wire that becomes magnetic only when an electric current flows through it. The magnetism of an electromagnet can be controlled by switching the current on or off.
How does Earth’s magnetic field protect us from solar radiation?
Earth’s magnetic field acts as a shield against harmful solar radiation. It deflects charged particles from the sun, such as protons and electrons, preventing them from reaching the Earth’s surface. This protective effect helps to maintain the atmosphere and makes life possible on Earth.
What is the significance of the magnetic hysteresis loop in materials?
The magnetic hysteresis loop represents the relationship between the magnetizing force and the resulting magnetization of a material. It provides important information about the material’s magnetic properties, such as coercivity, retentivity, and energy loss. This is crucial in determining the suitability of a material for various applications, like in transformers and magnetic storage devices.
Can all materials be magnetized? Why or why not?
Not all materials can be magnetized. Only certain materials, known as ferromagnetic materials (like iron, cobalt, and nickel), can be strongly magnetized. This is because their atomic structure allows for the alignment of magnetic moments in the same direction. Other materials, like paramagnetic and diamagnetic materials, exhibit much weaker magnetic properties and cannot be magnetized to the same extent.
How does temperature affect the magnetism of a material?
Temperature has a significant impact on the magnetism of a material. As temperature increases, the thermal energy causes the magnetic moments of atoms to become more disordered, reducing the material’s magnetism. At a certain temperature, known as the Curie temperature, a ferromagnetic material loses its magnetic properties entirely and becomes paramagnetic.