The story of magnetism begins with an ancient and naturally occurring mineral called lodestone. This special rock had the mysterious ability to attract pieces of iron, and it was this property that first introduced humans to the concept of magnetism. The name ‘magnet’ itself comes from the Greek word “magnētis lithos,” which means “Magnesian stone” or “lodestone”.
During the Middle Ages, people began to use the directional property of lodestones to navigate the seas. This led to the creation of the first simple compasses, which were crucial for maritime exploration. In the Renaissance, a significant leap in understanding came with William Gilbert’s work. In 1600, he published “De Magnete,” where he proposed that Earth itself is a giant magnet. This was a revolutionary idea that changed the way people understood the world.
The 19th century was a golden era for magnetism, where scientists like Hans Christian Ørsted, André-Marie Ampère, and Michael Faraday made groundbreaking discoveries. Ørsted discovered that electric currents create magnetic fields, Ampère developed the mathematical description of magnetic forces, and Faraday discovered electromagnetic induction.
It wasn’t until the 20th century that scientists fully understood the quantum mechanical origins of magnetism. They discovered that magnetism is due to the motion of electrons, and it’s a fundamental aspect of electromagnetism. This understanding has led to the development of various technologies we rely on today, from electric motors to MRI machines.
What is Magnetization?
Magnetization refers to the degree to which a material can be magnetized. It’s a measure of the density of aligned magnetic dipole moments in a magnetic material. When a material is placed in a magnetic field, its atomic dipoles align themselves with the field, causing the material to become magnetized.
Imagine you have a bunch of tiny compasses, each with a north and south pole. If you place these compasses in a random arrangement, they point in all different directions. This is similar to how the atoms in a non-magnetized material behave; their magnetic moments (which are like tiny compass needles) are all over the place.
Now, what happens when you bring a strong magnet close to these tiny compasses? They all start to align in the direction of the magnetic field created by the strong magnet. This alignment of the magnetic moments is what we call Magnetization.
In more technical terms, Magnetization (M) is a vector quantity that represents the density of permanent or induced magnetic dipole moments in a magnetic material. It’s the measure of the magnetic response of a material to an external magnetic field.
Magnetization occurs because of the behavior of electrons in atoms. Electrons have a property called ‘spin’, and when they move or spin, they create a tiny magnetic field. In most materials, these mini-magnetic fields cancel each other out because the electrons are paired up and spin in opposite directions. However, in magnetic materials, some of these electrons are unpaired, and their spins can align with an external magnetic field, causing the material to become magnetized.
Magnetization (M) is defined as the net magnetic moment per unit volume of a material. In mathematical terms, this is expressed as:
\(\displaystyle M = \frac{m_{\text{net}}}{V} \)
where (mnet) is the net magnetic moment and (V) is the volume of the material.
A solenoid is a coil of wire that generates a magnetic field when an electric current passes through it. If a solenoid has (n) turns per unit length and a current (I) flowing through it, the magnetic field inside the solenoid, (B0), is given by:
\(\displaystyle B_0 = \mu_0 n I \)
where (µ0) is the permeability of free space.
When we fill the solenoid with a material that can be magnetized, the total magnetic field inside the solenoid, (B), is the sum of the field due to the solenoid, (B0), and the field due to the material, (Bm):
\(\displaystyle B = B_0 + B_m \)
The field provided by the core material, (Bm), is proportional to the material’s magnetization:
\(\displaystyle B_m = \mu_0 M \)
Magnetic intensity, (H), is a measure of the magnetic field due to external factors, such as the current in the solenoid, and is defined as:
\(\displaystyle H = \frac{B}{\mu_0} – M \)
Using the definition of (H), we can express the total magnetic field (B) as:
\(\displaystyle B = \mu_0 (H + M) \)
Magnetic susceptibility, (χ), is a measure of how much a material will become magnetized in an applied magnetic field. For the material inside the solenoid, magnetization (M) is given by:
\(\displaystyle M = \chi H \)
By substituting the value of (M) into the equation for (B), we get:
\(\displaystyle B = \mu_0 (H + \chi H) = \mu_0 (1 + \chi) H = \mu_0 \mu_r H = \mu H \)
Here, (µr) is the relative magnetic permeability of the material, and ( \mu ) is the magnetic permeability, defined as:
\(\displaystyle \mu = \mu_0 \mu_r = \mu_0 (1 + \chi) \)
Through this derivation, we can see how the concepts of magnetization, magnetic field, and magnetic intensity are interconnected.
So, in essence, Magnetization is all about alignment and the collective behavior of atomic magnetic moments in response to an external magnetic field. It’s like a team of rowers in a boat; when everyone rows in the same direction, the boat moves swiftly and smoothly, just as material becomes strongly magnetized when all its atomic ‘rowers’ are aligned.
Magnetic Intensity or Intensity of Magnetic Field
Magnetic Intensity, also known as the Intensity of Magnetic Field or Magnetic Field Strength (H), is a measure of the strength of a magnetic field at a point. It is determined by the force that the field would exert on a moving charge or on a magnetic pole at that point.
Magnetic Intensity (H) is a measure of the strength of a magnetic field applied to a material. It’s like the push that a magnetic field gives to align the magnetic moments within a material. Think of it as the effort you need to apply to push a shopping cart; the harder you push, the faster the cart moves. Similarly, the greater the magnetic intensity, the stronger the magnetic field.
Magnetic Intensity is measured in Amperes per meter (A/m). It’s a vector quantity, which means it has both magnitude and direction.
Factors Affecting Magnetic Intensity: The intensity of the magnetic field depends on factors like:
- The current flows through a wire.
- The number of turns in a coil if we’re talking about a solenoid.
- The distance from the source of the magnetic field.
Imagine you have a coil of wire, known as a solenoid. When an electric current flows through this coil, it creates a magnetic field inside and around the coil. The strength of this field inside the solenoid can be described by its magnetic intensity.
Magnetic Intensity is crucial when we talk about magnetizing a material. When you place a material inside a solenoid, the magnetic intensity of the solenoid’s field will start aligning the magnetic moments of the material, leading to its magnetization.
Mathematically, the magnetic intensity H can be related to the total magnetic field B and the magnetization M of a material through the equation:
\(\displaystyle B = \mu_0 (H + M) \)
where (µ0) is the permeability of free space. This equation shows how the external magnetic field (H) and the material’s response to it (M) combine to produce the total magnetic field (B).
The intensity of the magnetic field at point P due to a single pole:
The intensity of the magnetic field at a point due to a single pole is like the strength of the magnetic force you would feel if you were standing at that point with a tiny compass. It tells us how strong the magnetic ‘push’ is at that specific location.
Consider a magnetic pole with a pole strength of (m). This pole creates a magnetic field around it. Now, let’s say we want to find the magnetic field intensity at a point ‘P’ that is a distance (r) away from our magnetic pole.
The formula to calculate the intensity of the magnetic field at point P is given by:
\(\displaystyle B = \frac{\mu_0 \cdot m}{4\pi \cdot r^2}\)
- (B) is the magnetic field intensity,
- (µ0) is the permeability of free space,
- (m) is the pole strength of the magnet,
- (r) is the distance from the pole to point P.
The equation tells us that the magnetic field intensity is directly proportional to the pole strength and inversely proportional to the square of the distance from the pole. This is similar to how the brightness of light decreases as you move away from the source.
Intensity of Magnetic Field Due to a Magnet at Different Points
The intensity of the magnetic field due to a magnet varies depending on the position relative to the magnet:
(i) In Longitudinal Position: The field lines are parallel to the axis of the magnet, and the intensity is stronger at the poles.
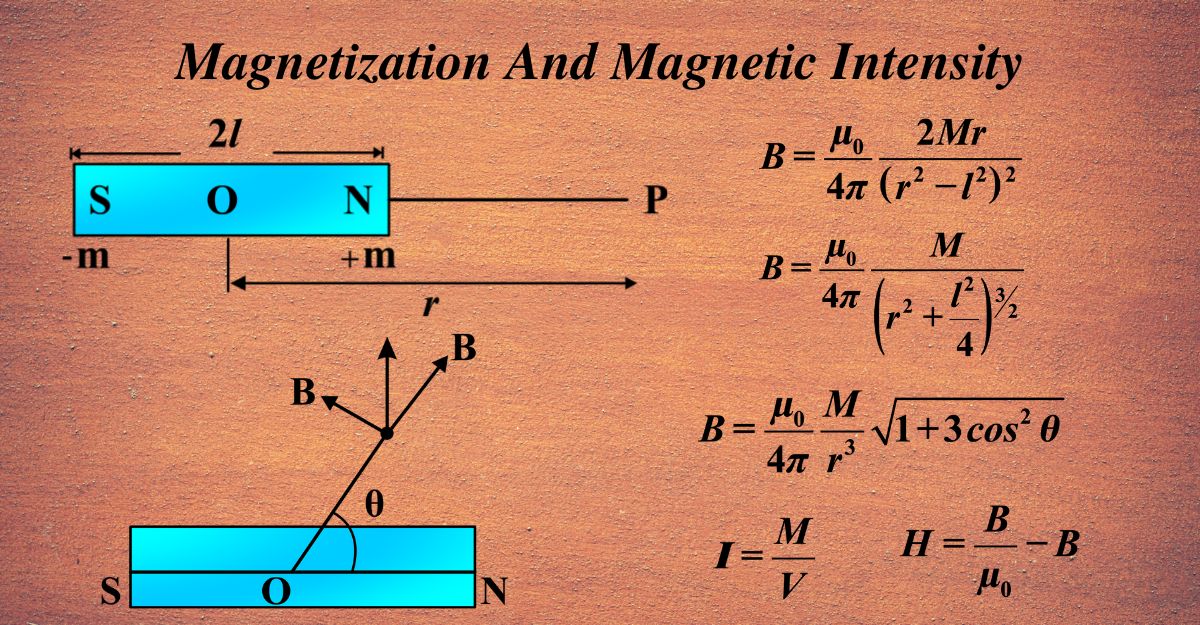
Consider a bar magnet with its north pole labeled as ‘+m’ and south pole as ‘-m’. The magnet is placed along the x-axis of a coordinate system with the origin ‘O’ at its center. We want to find the intensity of the magnetic field at a point ‘P’ located at a distance ‘r’ from the center of the magnet on this axis.
The intensity of the magnetic field at point P in the longitudinal position is given by:
\(\displaystyle B = \frac{\mu_0}{4\pi} \times \frac{2Mr}{(r^2 – l^2)^2} \)
- (µ0) is the permeability of free space,
- (M) is the magnetic moment of the magnet, which equals (\(\displaystyle 2 \times m \times l \)),
- (m) represents the magnitude of the magnetic poles,
- (l) is half the length of the bar magnet,
- (r) is the distance from the center of the magnet to point P.
For cases where (r) is much greater than (l), meaning point P is far from the magnet compared to its size, we can simplify the formula:
\(\displaystyle B = \frac{\mu_0}{4\pi} \times \frac{2Mr}{r^3} = \frac{\mu_0}{4\pi} \times \frac{2M}{r^3} \)
This derivation helps us understand how the intensity of the magnetic field varies with distance from a magnet when measured along its length. It’s a key concept in magnetism and is particularly useful when studying the effects of magnetic fields at points far from the physical size of the magnet. Remember, the intensity decreases with the cube of the distance in the longitudinal position.
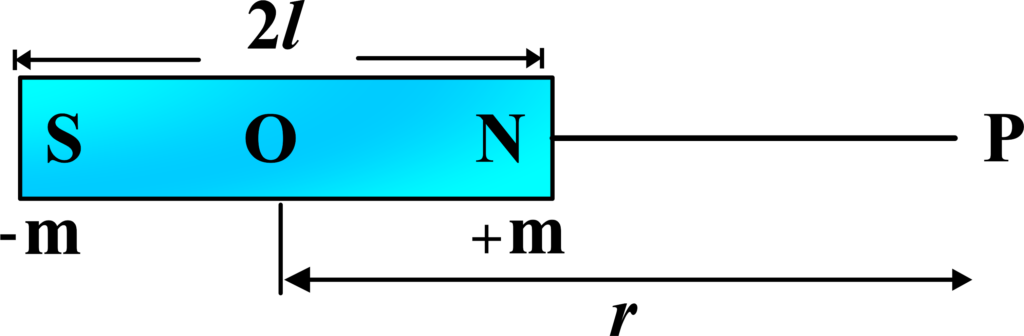
(ii) In Transverse Position: The field lines are perpendicular to the axis of the magnet, and the intensity is weaker compared to the longitudinal position.
Imagine a bar magnet lying horizontally and we want to find the magnetic field intensity at a point ‘P’ that is above the center of the magnet, at a perpendicular distance ‘r’. The intensity of the magnetic field at point P in the transverse position is given by:
\(\displaystyle B = \frac{\mu_0}{4\pi} \cdot \frac{M}{(r^2 + \frac{l^2}{4})^{3/2}} \)
If the magnet is short, meaning (l) is much smaller than (r), the formula simplifies to:
\(\displaystyle B = \frac{\mu_0}{4\pi} \cdot \frac{2M}{r^3} \)
In the transverse position, the magnetic field intensity decreases with the cube of the distance from the magnet, just like in the longitudinal position. However, the field strength is generally weaker in the transverse position compared to the longitudinal position for the same distance ‘r’.
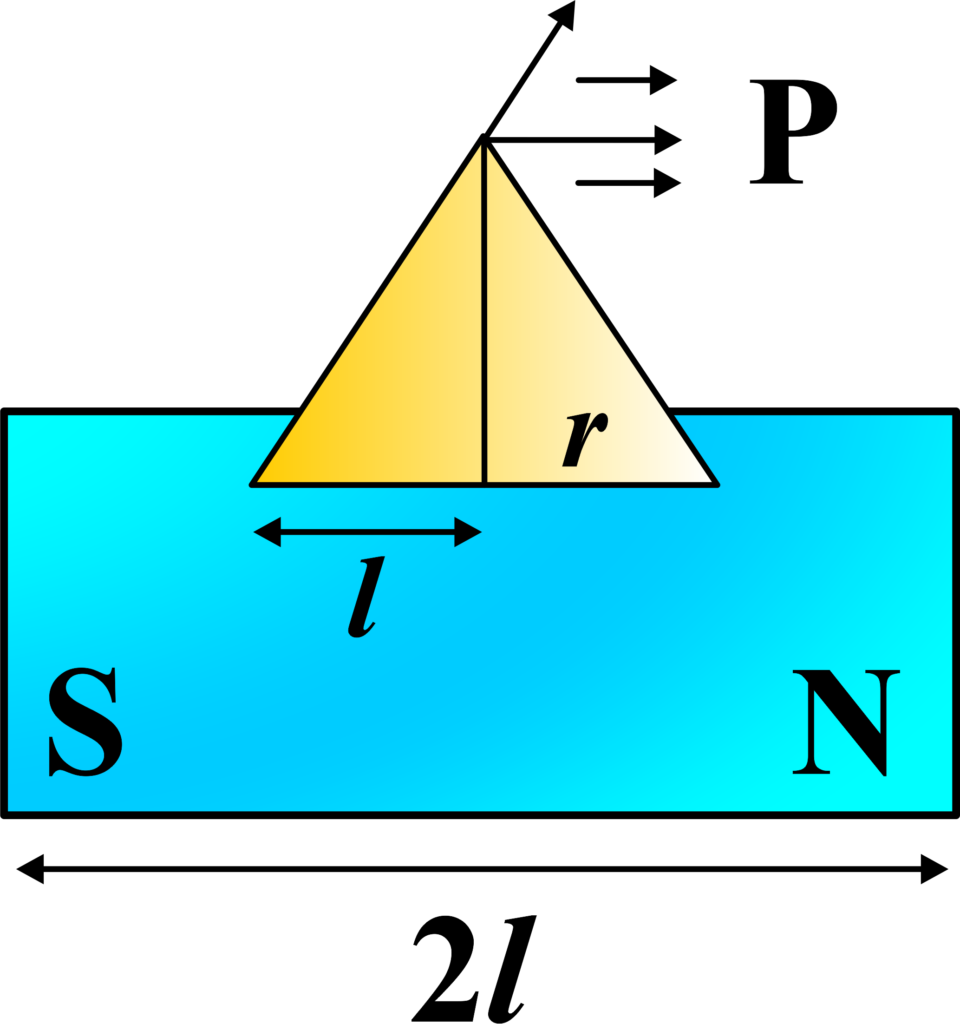
(iii) In Any General Position: The intensity can be calculated using the law of cosines, considering the angle between the position vector and the axis of the magnet.
Imagine a bar magnet with its north and south poles. We want to find the magnetic field intensity at an arbitrary point ‘P’ that is at a distance ‘r’ from the center of the magnet and at an angle ‘θ’ with the axis of the magnet.
The magnetic field has two components:
- (Br): The component parallel to the axis of the magnet.
- (Bg): The component perpendicular to the axis of the magnet.
The intensity of the magnetic field components at point P is given by:
For (Br):
\(\displaystyle B_r = \frac{\mu_0}{4\pi} \cdot \frac{2M \cos \theta}{r^3} \)
For (Bg):
\(\displaystyle B_g = \frac{\mu_0}{4\pi} \cdot \frac{M \sin \theta}{r^3} \)
To find the total magnetic field intensity (B) at point P, we combine the two components:
\(\displaystyle B = \sqrt{B_r^2 + B_g^2} \)
Substituting the expressions for (Br) and (Bg), we get:
\(\displaystyle B = \sqrt{\left(\frac{\mu_0}{4\pi} \cdot \frac{2M \cos \theta}{r^3}\right)^2 + \left(\frac{\mu_0}{4\pi} \cdot \frac{M \sin \theta}{r^3}\right)^2} \)
After simplifying the above expression, we arrive at the formula for the total magnetic field intensity at point P in any general position:
\(\displaystyle B = \frac{\mu_0}{4\pi} \cdot \frac{M}{r^3} \cdot \sqrt{1 + 3\cos^2 \theta} \)
The total magnetic field intensity at any general position around a magnet depends on the distance from the magnet and the angle with respect to the magnet’s axis. This formula helps students understand how magnetic fields behave in space around a magnet, which is crucial for many applications in physics and engineering. Remember, the direction of (Br) is always parallel to the axis from the north to the south pole of the magnet.
What is the Intensity of Magnetisation
Definition: Intensity of Magnetisation (I) is a measure of how much a material is magnetized. It’s defined as the magnetic moment per unit volume of the material¹. In simpler terms, it tells us how strong the magnetic ‘personality’ of a material is.
The formula for the Intensity of Magnetisation is:
\(\displaystyle I = \frac{M}{V} \)
- (I) is the Intensity of Magnetisation,
- (M) is the total magnetic moment,
- (V) is the volume of the material.
Unit: The SI unit of Intensity of Magnetisation is Ampere per meter (A/m).
Think of the Intensity of Magnetisation like the density of a crowd at a concert. Just as crowd density tells us how many people are packed into a certain area, Intensity of Magnetisation tells us how much magnetic moment is packed into a material’s volume.
Difference between Magnetic Intensity and Intensity of Magnetisation
Magnetic Intensity (H):
Definition: Magnetic Intensity, also known as Magnetic Field Strength (H), is a measure of the strength of a magnetic field at a point. It’s like the ‘push’ or ‘pull’ you feel when you bring a magnet close to metal objects.
The formula for Magnetic Intensity is:
\(\displaystyle H = \frac{B}{\mu_0} – M \)
where (B) is the magnetic flux density, (µ0) is the permeability of free space, and (M) is the magnetization. The unit of Magnetic Intensity is Ampere per meter (A/m). Magnetic intensity represents the external magnetic field applied to a material, without considering the material’s response.
Intensity of Magnetisation (I):
Definition: Intensity of Magnetisation (I) is a measure of the degree to which a material is magnetized. It’s like the ‘magnetism’ that a material gains in response to an applied magnetic field.
The formula for the Intensity of Magnetisation is:
\(\displaystyle I = \frac{M}{V} \)
where (M) is the magnetic moment and (V) is the volume of the material. The unit of Intensity of Magnetisation is also Ampere per meter (A/m). It represents the material’s internal magnetization, which is its response to the applied magnetic field.
Key Differences:
- Origin: Magnetic Intensity is an external factor determined by the applied magnetic field, while Intensity of Magnetisation is an internal property showing how the material itself has been magnetized.
- Dependence: Magnetic Intensity depends on the source of the magnetic field (like a current-carrying wire or a magnet), whereas the Intensity of Magnetisation depends on the material’s properties and how it reacts to the external magnetic field.
- Relation: The intensity of Magnetisation can be influenced by Magnetic Intensity, but not vice versa. When you increase the Magnetic Intensity, the Intensity of Magnetisation can increase if the material is capable of being magnetized.
In simple terms, Magnetic Intensity is about the external ‘effort’ applied to create a magnetic field, and the Intensity of Magnetisation is about the material’s internal ‘response’ to that effort. Understanding this distinction is crucial when studying how different materials behave in magnetic fields and has practical applications in designing electrical devices and understanding magnetic materials.
Also Read: Magnetic Field of Earth
Solved Examples
Problem 1: A bar magnet of length (10 cm) and magnetic moment (2 A∙m2) is placed with its axis along the x-axis. Calculate the magnetic field at a point (20 cm) away from the center of the magnet on its axial line.
Solution: The magnetic field (B) in the longitudinal position is given by:
\(\displaystyle B = \frac{\mu_0}{4\pi} \cdot \frac{2Mr}{(r^2 – l^2)^2} \)
Given: Length of the magnet (\(\displaystyle 2l = 10 \, \text{cm} = 0.10 \, \text{m} ), hence ( l = 0.05 \, \text{m} \)); Magnetic moment (\(\displaystyle M = 2 \, \text{A} \cdot \text{m}^2 \)); Distance (\(\displaystyle r = 20 \, \text{cm} = 0.20 \, \text{m} \))
\(\displaystyle B = \frac{4\pi \times 10^{-7}}{4\pi} \cdot \frac{2 \times 2 \times 0.20}{(0.20^2 – 0.05^2)^2} \)
\(\displaystyle B = 10^{-7} \cdot \frac{0.80}{(0.04 – 0.0025)^2} \)
\(\displaystyle B = 10^{-7} \cdot \frac{0.80}{0.0375^2} \)
\(\displaystyle B = 10^{-7} \cdot \frac{0.80}{0.00140625} \)
\(\displaystyle B = 10^{-7} \cdot 568.18 \)
\(\displaystyle B \approx 5.68 \times 10^{-5} \, \text{T} \)
The magnetic field at a point (20 cm) away from the center of the magnet on its axial line is approximately (\(\displaystyle 5.68 \times 10^{-5} \, \text{T} \)).
Problem 2: A bar magnet of length (8 cm) and magnetic moment (\(\displaystyle 1.5 \, \text{A} \cdot \text{m}^2 \)) is placed with its axis perpendicular to the line joining the center of the magnet to the observation point. Calculate the magnetic field at a point (12 cm) away from the center of the magnet on this transverse line.
Solution: The magnetic field (B) in the transverse position is given by:
\(\displaystyle B = \frac{\mu_0}{4\pi} \cdot \frac{M}{(r^2 + \frac{l^2}{4})^{3/2}} \)
Given: Length of the magnet (\(\displaystyle 2l = 8 \, \text{cm} = 0.08 \, \text{m} \)), hence (l = 0.04 m); Magnetic moment (\(\displaystyle M = 1.5 \, \text{A} \cdot \text{m}^2 \)); Distance ( r = 12 cm = 0.12 m).
\(\displaystyle B = \frac{4\pi \times 10^{-7}}{4\pi} \cdot \frac{1.5}{(0.12^2 + \frac{0.04^2}{4})^{3/2}} \)
\(\displaystyle B = 10^{-7} \cdot \frac{1.5}{(0.0144 + 0.0004)^{3/2}} \)
\(\displaystyle B = 10^{-7} \cdot \frac{1.5}{0.0148^{3/2}} \)
\(\displaystyle B = 10^{-7} \cdot \frac{1.5}{0.001804} \)
\(\displaystyle B \approx 10^{-7} \cdot 831.16 \)
\(\displaystyle B \approx 8.31 \times 10^{-5} \, \text{T} \)
The magnetic field at a point (12 cm) away from the center of the magnet on its transverse line is approximately (\(\displaystyle 8.31 \times 10^{-5} \, \text{T} \)).
Problem 3: A bar magnet with a magnetic moment of (\(\displaystyle 2 \, \text{A} \cdot \text{m}^2 \)) is placed such that the angle between its axis and the line joining the center of the magnet to the observation point is (45∘). Calculate the magnetic field at a point (10cm) away from the center of the magnet.
Solution: The magnetic field (B) in any general position is given by:
\(\displaystyle B = \frac{\mu_0}{4\pi} \cdot \frac{M}{r^3} \cdot \sqrt{1 + 3\cos^2 \theta} \)
Given: Magnetic moment (\(\displaystyle M = 2 \, \text{A} \cdot \text{m}^2 \)); Distance ( r = 10 cm = 0.10 m); Angle (θ= 45∘)
\(\displaystyle B = \frac{4\pi \times 10^{-7}}{4\pi} \cdot \frac{2}{(0.10)^3} \cdot \sqrt{1 + 3\cos^2 45^\circ} \)
\(\displaystyle B = 10^{-7} \cdot \frac{2}{0.001} \cdot \sqrt{1 + 3 \times \frac{1}{2}} \)
\(\displaystyle B = 10^{-7} \cdot 2000 \cdot \sqrt{1 + 1.5} \)
\(\displaystyle B = 10^{-7} \cdot 2000 \cdot \sqrt{2.5} \)
\(\displaystyle B = 10^{-7} \cdot 2000 \cdot 1.581 \)
\(\displaystyle B \approx 3.162 \times 10^{-4} \, \text{T} \)
The magnetic field at a point (10 cm) away from the center of the magnet at an angle of (45∘) is approximately (\(\displaystyle 3.162 \times 10^{-4} \, \text{T} \)).
Problem 4: A cylindrical rod of magnetic material has a magnetization (M = 2000 A/m). If the length of the rod is (0.5 m) and the area of the cross-section is (1 cm2), calculate the magnetic moment of the rod.
Solution: Magnetization (M) is related to the magnetic moment (m) by:
\(\displaystyle M = \frac{m}{V} \)
Given: Magnetization (M = 2000 A/m); Length (l = 0.5 m); Area of cross-section (\(\displaystyle A = 1 \, \text{cm}^2 = 1 \times 10^{-4} \, \text{m}^2 \))
Volume (V) is:
\(\displaystyle V = A \times l = 1 \times 10^{-4} \, \text{m}^2 \times 0.5 \, \text{m} \)
\(\displaystyle V = 0.5 \times 10^{-4}\, \text{m}^3 \)
Magnetic moment (m) is:
\(\displaystyle m = M \times V = 2000 \, \text{A/m} \times 0.5 \times 10^{-4} \, \text{m}^3 \)
\(\displaystyle m = 1000 \times 10^{-4} \, \text{A} \cdot \text{m}^2 \)
\(\displaystyle m = 0.1 \, \text{A} \cdot \text{m}^2 \)
The magnetic moment of the rod is (\(\displaystyle 0.1 \, \text{A} \cdot \text{m}^2 \)).
Problem 5: A solenoid of length (0.5 m) and (1000) turns carries a current of (2 A). Calculate the intensity of the magnetic field inside the solenoid.
Solution: The intensity of the magnetic field (H) inside a solenoid is given by:
H = nI
Given: Length of the solenoid (l = 0.5 m); Total number of turns (N = 1000); Current (I = 2 A).
The number of turns per unit length (n) is:
\(\displaystyle n = \frac{N}{l} = \frac{1000}{0.5} = 2000 \, \text{turns/m} \)
The intensity of the magnetic field (H) is:
\(\displaystyle H = 2000 \, \text{turns/m} \times 2 \, \text{A} \)
H = 4000 A/m
The intensity of the magnetic field inside the solenoid is (4000 A/m).
Problem 6: A bar magnet of length (12 cm) and magnetic moment (\(\displaystyle 3 \, \text{A} \cdot \text{m}^2 \)) is placed with its axis along the y-axis. Calculate the magnetic field at a point (15 cm) away from the center of the magnet on its axial line.
Solution: The magnetic field (B) in the longitudinal position is given by:
\(\displaystyle B = \frac{\mu_0}{4\pi} \cdot \frac{2Mr}{(r^2 – l^2)^2} \)
Given: Length of the magnet (\(\displaystyle 2l = 12 \, \text{cm} = 0.12 \, \text{m} \)), hence (l = 0.06m); Magnetic moment (\(\displaystyle M = 3 \, \text{A} \cdot \text{m}^2 \)); Distance (r = 15 cm = 0.15 m).
\(\displaystyle B = \frac{4\pi \times 10^{-7}}{4\pi} \cdot \frac{2 \times 3 \times 0.15}{(0.15^2 – 0.06^2)^2} \)
\(\displaystyle B = 10^{-7} \cdot \frac{0.90}{(0.0225 – 0.0036)^2} \)
\(\displaystyle B = 10^{-7} \cdot \frac{0.90}{0.0189^2} \)
\(\displaystyle B = 10^{-7} \cdot \frac{0.90}{0.00035721} \)
\(\displaystyle B = 10^{-7} \cdot 2519.2 ]\)
\(\displaystyle B \approx 2.52 \times 10^{-4} \, \text{T} \)
The magnetic field at a point (15 cm) away from the center of the magnet on its axial line is approximately (\(\displaystyle 2.52 \times 10^{-4} \, \text{T}\) ).
Problem 7: A material has a magnetic field (B = 0.005 T) and a magnetization (M = 500 A/m). Calculate the magnetic intensity (H) in the material.
Solution: The magnetic intensity (H) is given by the formula:
\(\displaystyle H = \frac{B}{\mu_0} – M \)
Given: Magnetic field (B = 0.005 T); Magnetization (M = 500 A/m);
First, we calculate (\(\displaystyle\frac{B}{\mu_0}\)):
\(\displaystyle \frac{B}{\mu_0} = \frac{0.005 \, \text{T}}{4\pi \times 10^{-7} \, \text{T} \cdot \text{m/A}} \)
\(\displaystyle \frac{B}{\mu_0} = \frac{0.005}{4\pi \times 10^{-7}} \)
\(\displaystyle \frac{B}{\mu_0} = \frac{0.005}{1.25664 \times 10^{-6}} \)
\(\displaystyle\frac{B}{\mu_0} = 3978.87 \, \text{A/m} \)
Next, we substitute this value and (M) into the formula for (H):
\(\displaystyle H = 3978.87 \, \text{A/m} – 500 \, \text{A/m} \)
\(\displaystyle H = 3478.87 \, \text{A/m} \)
The magnetic intensity (H) in the material is (3478.87 A/m).
FAQs
What is magnetization?
Magnetization is a measure of the magnetic moment per unit volume of a material. It indicates how much a material is magnetized when exposed to an external magnetic field and is often represented by the symbol (M).
How is magnetic intensity different from magnetization?
Magnetic intensity, also known as magnetic field strength, is the measure of the strength of a magnetic field applied to a material. It is represented by the symbol (H) and describes the ability of the external field to magnetize a material. Unlike magnetization, it does not depend on the properties of the material itself.
What factors affect the magnetization of a material?
The magnetization of a material is influenced by several factors, including the strength of the external magnetic field, the temperature of the material, and the material’s intrinsic properties, such as its magnetic susceptibility and type (ferromagnetic, paramagnetic, or diamagnetic).
What is the relationship between magnetization and magnetic intensity?
The relationship between magnetization (M) and magnetic intensity (H) is given by the material’s magnetic susceptibility (Χ). The magnetization is proportional to the magnetic intensity, with the proportionality constant being the magnetic susceptibility: (\(\displaystyle M = \chi H \)).
How do ferromagnetic, paramagnetic, and diamagnetic materials differ in terms of magnetization?
- Ferromagnetic materials have a strong positive magnetization even in the absence of an external magnetic field. They can retain their magnetization, making them suitable for permanent magnets.
- Paramagnetic materials have a weak positive magnetization that is directly proportional to the external magnetic field and disappears when the field is removed.
- Diamagnetic materials exhibit a weak negative magnetization in the presence of an external magnetic field, causing them to be repelled by the field.
What is the significance of the magnetic hysteresis loop?
The magnetic hysteresis loop represents the relationship between the magnetization of a material and the external magnetic field intensity. It shows how the material’s magnetization changes as the external field is cycled. The loop’s shape provides information about the material’s coercivity, retentivity, and energy loss during the magnetization process.
How does temperature affect magnetization?
Temperature has a significant impact on magnetization. For ferromagnetic materials, increasing temperature can reduce magnetization. At a certain temperature called the Curie temperature, ferromagnetic materials lose their magnetization and become paramagnetic. Paramagnetic and diamagnetic materials are less affected by temperature changes, but their magnetic susceptibility can still vary with temperature.