Mirror Equation

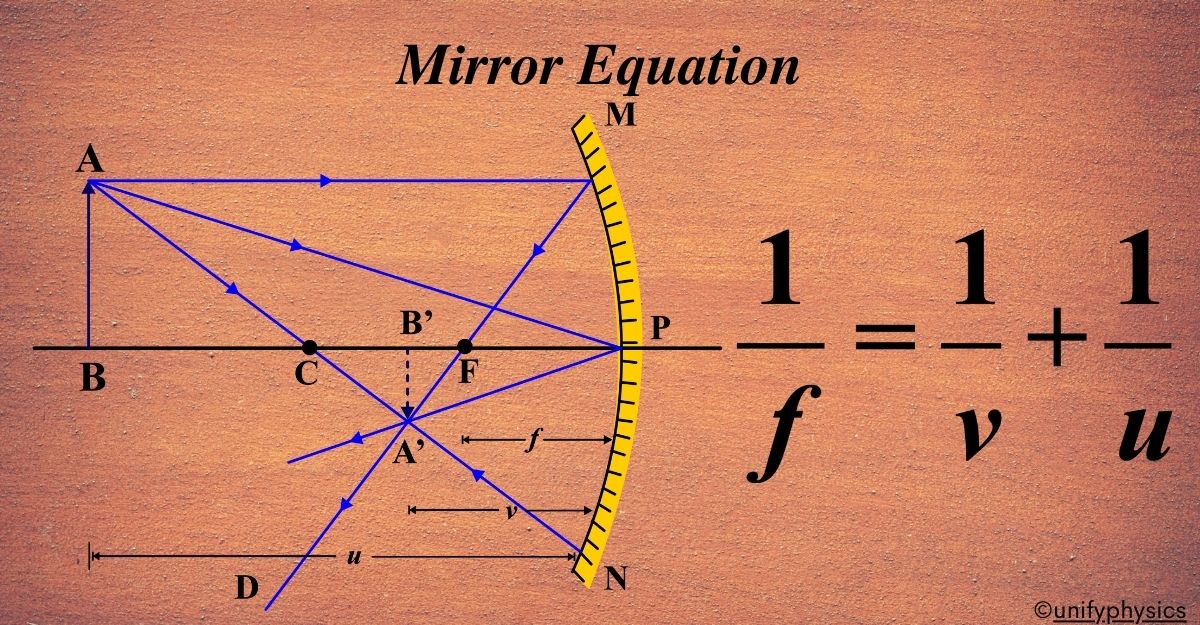
The mirror equation is a fundamental concept in the field of optics, which is the branch of physics that deals with the behavior and properties of light. The origins of the mirror equation can be traced back to the works of ancient scholars who were fascinated by the properties of light and reflection.

The earliest mirrors were simply polished surfaces, like still water or shiny metals, which people used to see their reflections. These weren’t used for scientific purposes but laid the groundwork for understanding reflective surfaces.

In classical antiquity, Greek and Roman scholars began to study the properties of light and reflection more systematically. However, the mathematical relationships governing reflection were not yet formulated.

A significant leap in the study of optics came during the Islamic Golden Age. Scholars like Ibn al-Haytham, also known as Alhazen, made groundbreaking contributions. In his seminal work, “Book of Optics” (Kitab al-Manazir), he discussed various optical phenomena and laid the foundation for the scientific method.

During the Renaissance, the study of optics flourished again. Scientists like Johannes Kepler and others began to describe the laws of reflection and refraction more precisely, although the mirror equation as we know it today had not yet been formulated.

It was during the Scientific Revolution that the mirror equation began to take shape. Isaac Newton and other scientists of the era made extensive studies of light and mirrors, leading to a more comprehensive understanding of optics.

The modern mirror equation, which relates the object distance (u), the image distance (v), and the focal length (f) of a spherical mirror, was eventually derived from these early studies. It is a quantitative tool that allows us to predict the behavior of light when it reflects off mirrors, especially spherical ones.

What is a Mirror?

A mirror is a surface, typically of glass with a reflective coating, that reflects light in such a way that it preserves much of the original image’s characteristics. The most common mirror is the plane mirror, which forms images that are virtual, upright, and the same size as the object.

A mirror is much more than just a tool for checking your appearance. In physics, a mirror is defined as a surface that reflects light to form images of objects placed in front of it. This reflection happens in a very specific and predictable way, which is why mirrors are such an important topic in optics, the study of light.

When light rays hit a mirror, they bounce off its surface. This process is known as reflection. The laws of reflection govern how these light rays behave. According to these laws:

• The incident ray (the incoming light ray) and the reflected ray (the light ray that bounces off) make the same angle with a line called the normal. The normal is an imaginary line perpendicular to the surface at the point where the light ray hits.
• The incident ray, the reflected ray, and the normal all lie in the same plane.

For a good quality mirror, the surface must be very smooth. If the surface is rough, the light scatters in many directions, and you don’t get a clear reflection. The smoothness of the mirror’s surface is crucial because it ensures that the reflection of light is specular. This means that the light rays reflect in a single, predictable direction, as opposed to diffuse reflection, where light scatters randomly.

Mirrors can be made from a variety of materials, but most commonly, they are made of glass with a reflective coating on one side. This coating is often made of metals like silver or aluminum, which are chosen for their high reflectivity. In essence, a mirror is a unique surface that follows the laws of reflection to create an image that the observer can see.

Types of Mirrors

There are mainly two types of mirrors:

Plane Mirrors

Flat mirrors that reflect images with the same size and orientation as the original object. Plane mirrors are the simplest type of mirror and are fundamental in the study of optics. A plane mirror is essentially a flat mirror that reflects light in a consistent manner, adhering to the laws of reflection.

When light rays strike a plane mirror, the angle at which they hit the mirror (the angle of incidence) is equal to the angle at which they reflect off the mirror (the angle of reflection). This occurs because plane mirrors have a smooth surface that causes specular reflection, where the light rays reflect in a single, predictable direction.

Characteristics of Images Formed by Plane Mirrors:

• The images formed by plane mirrors are always virtual; that is, they cannot be projected onto a screen because the light rays do not converge.
• These images are upright and maintain the same orientation as the object being reflected.
• The size of the image is the same as the size of the object.
• Interestingly, plane mirrors create a lateral inversion of the image. This means that the object’s left side appears on the image’s right side, and vice versa.

Understanding Reflection in Plane Mirrors: Reflection in plane mirrors is governed by two types:

• Specular/Regular Reflection: This occurs when light rays reflect off a smooth surface, like a plane mirror, and remain uniformly distributed.
• Diffused/Irregular Reflection: This happens when light reflects off a rough surface, causing the light rays to scatter in many directions.

Spherical Mirrors

Spherical mirrors: Curved mirrors that are part of a sphere. These can be further divided into:

Concave mirrors:

Curved inward, can form real or virtual images depending on the object’s position. Concave mirrors, also known as converging mirrors, are a type of spherical mirror with a reflective surface that curves inward, like the inside of a sphere.

Understanding Concave Mirrors:

• Shape: The reflective surface of a concave mirror is a part of the interior of a sphere. This means that if you continued the curve of the mirror all the way around, it would form a complete sphere.
• Focal Point: One of the key characteristics of concave mirrors is their ability to converge light rays. When parallel light rays (like those coming from a distant object) hit a concave mirror, they reflect and meet at a single point called the focal point.
• Image Formation: The images formed by concave mirrors can be real or virtual, depending on the position of the object relative to the focal point and the mirror. Real images are formed when light rays converge, while virtual images appear to come from a point behind the mirror.

Concave mirrors are fascinating because they can produce such a wide range of image types. They are a great example of how the principles of geometry and optics come together to create complex and useful phenomena.

Convex mirrors:

Curved outward, always form virtual, diminished images.

• Curvature: Unlike concave mirrors that curve inward, convex mirrors have a reflective surface that bulges outward. Imagine the outside of a shiny, round ball; that’s similar to the surface of a convex mirror.
• Diverging Light Rays: When parallel light rays hit a convex mirror, they reflect and spread out (diverge). This is why they’re called diverging mirrors.
• Focal Point: Even though the light rays diverge, they seem to come from a common point behind the mirror, known as the focal point. However, this point is virtual because the light rays don’t come together at this point.

Image Formation by Convex Mirrors:

• Virtual Images: Convex mirrors always form virtual images, which means the images can’t be projected onto a screen because they don’t exist at the point where they appear to be.
• Upright and Diminished: The images formed are upright (erect) and smaller (diminished) compared to the actual object, no matter how far or close the object is to the mirror.
• Field of View: One of the key characteristics of convex mirrors is their wide field of view. They allow you to see more of the area behind you than plane or concave mirrors would.

Mirror Equation

The mirror equation is a powerful tool in optics that relates three important quantities: the object distance (u), the image distance (v), and the focal length (f) of a spherical mirror. It’s a formula that helps us understand where an image will form when light reflects off a mirror and how the image’s characteristics are related to the object and the mirror itself.

The mirror equation is elegantly simple:

\(\displaystyle\begin{equation}\label{eqn:1}\boxed{\boldsymbol{ \frac{1}{f} = \frac{1}{v} + \frac{1}{u}}} \end{equation}\)

• Object Distance (u): This is the distance from the object to the mirror.
• Image Distance (v): This is the distance from the image to the mirror.
• Focal Length (f): This is the distance from the focal point to the mirror. The focal point is where light rays that come in parallel to the principal axis converge (or appear to diverge from, in the case of a convex mirror).

When you place an object in front of a mirror, light rays reflect off the mirror and form an image. The position of this image and its characteristics (like size and orientation) depend on the object’s distance from the mirror and the mirror’s curvature, which is related to the focal length.

For Concave Mirrors:

• If the object is beyond the focal point, the image is real and inverted.
• If the object is at the focal point, the image forms at infinity.
• If the object is between the focal point and the mirror, the image is virtual, upright, and enlarged.

For Convex Mirrors:

• The image is always virtual, upright, and smaller than the object, no matter where the object is placed.

The mirror equation applies to both concave and convex mirrors and is a fundamental concept for understanding how mirrors affect light to create images.

Mirror Equation Derivation

The derivation of the mirror equation involves using the principles of geometry and optics, particularly the law of reflection. The given diagram shows the image (A’B’) of an object (AB) formed by a concave mirror. The image is real and inverted, and the rays reflect according to the laws of reflection. We’ll use the given information and the principles of similar triangles to derive the mirror equation, which relates the object distance (u), the image distance (v), and the focal length (f).

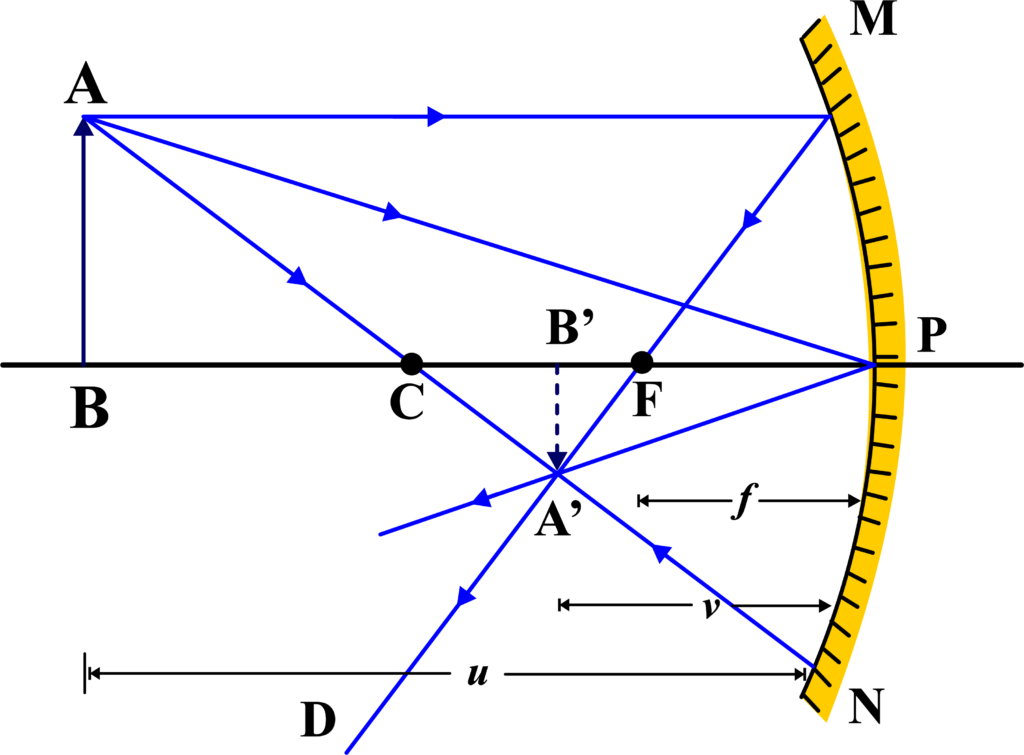
In the diagram, consider two pairs of similar triangles:

• ( \(\displaystyle\triangle A’B’F \)) and (\(\displaystyle \triangle MPF\) )
• (\(\displaystyle \triangle A’B’P\) ) and ( \(\displaystyle\triangle ABP\) )

Using Similar Triangles ( \(\displaystyle\triangle A’B’F\) ) and ( \(\displaystyle\triangle MPF\) ):

Since these triangles are similar:

\(\displaystyle\frac{B’A’}{PM} = \frac{B’F}{FP}\)

Given that ( PM = AB ):

\(\displaystyle\frac{B’A’}{AB} = \frac{B’F}{FP} \quad \text{(Equation 1)}\)

Using Similar Triangles (\(\displaystyle \triangle A’B’P\) ) and ( \(\displaystyle\triangle ABP\) ):

Since these triangles are similar:

\(\displaystyle\frac{B’A’}{BA} = \frac{B’P}{BP}\)

Given that ( BA = AB ):

\(\displaystyle\frac{B’A’}{AB} = \frac{B’P}{BP} \quad \text{(Equation 2)}\)

Comparing Equation (1) and Equation (2):

By comparing the two equations:

\(\displaystyle\frac{B’F}{FP}= \frac{B’P-FP}{FP}= \frac{B’P}{BP}\)

• ( B’P = -v ) (since the image is formed on the opposite side of the object)
• ( FP = –f ) (since the focal point is on the same side as the object for a concave mirror)
• ( BP = -u ) (the object distance) Substituting these into the equations, we get:

\(\displaystyle\frac{-v+f}{-f} = \frac{-v}{-u}\)

Simplifying, we obtain:

\(\displaystyle\frac{v-f}{f} = \frac{v}{u}\)

\(\displaystyle\frac{v}{f} = 1+ \frac{v}{u}\)

Dividing both sides by ( v ) we get:

\(\displaystyle\begin{equation}\label{eqn:2}\boxed{\boldsymbol{\frac{1}{v} + \frac{1}{u} = \frac{1}{f} }} \end{equation}\)

This relation is known as the mirror equation. The mirror equation ( \(\displaystyle\frac{1}{v} + \frac{1}{u} = \frac{1}{f} \)) is derived using the properties of similar triangles and the geometric relationships in the ray diagram. This equation is fundamental in understanding the behavior of light in concave mirrors, allowing us to determine the position of the image formed for any given object distance.

Sign Conventions for Mirror Equation

Sign conventions help us determine the nature and position of the image formed by mirrors.

Object Distance (u):

• The distance from the object to the mirror is called the object distance.
• It is considered negative if the object is placed in front of the mirror, which is the usual case.

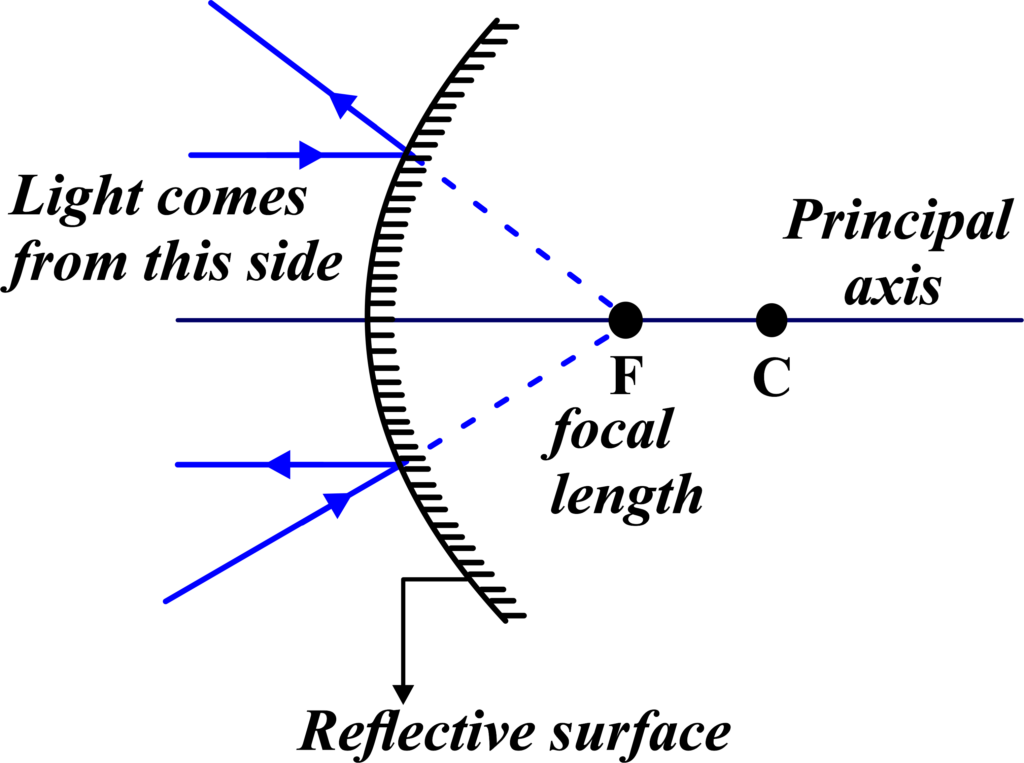
Image Distance (v):

• The distance from the image to the mirror is called the image distance.
• It is positive if the image is formed in front of the mirror (real image) and negative if formed behind the mirror (virtual image).

Focal Length (f):

• The distance from the principal focus to the mirror is called the focal length.
• For concave mirrors, it is positive because the focal point is in front of the mirror.
• For convex mirrors, it is negative because the focal point is behind the mirror.

Heights:

• Heights measured above the principal axis are positive.
• Heights measured below the principal axis are negative.

These sign conventions are part of the New Cartesian Sign Convention, which is universally accepted to avoid confusion in ray optics.

Also Read: Reflection of Light by Spherical Mirrors

Mirror Equation Applications

The mirror equation is not just a theoretical concept; it has practical applications that are quite significant in various fields.

Predicting Image Distance: If you know the distance between an object and a mirror, as well as the mirror’s focal length, you can use the mirror equation to calculate where the image will form.

Determining Object Distance: Conversely, if you know where the image is formed and the focal length of the mirror, the mirror equation can help you find out how far the actual object is from the mirror³.

Designing Optical Devices: The mirror equation is crucial in designing optical instruments like telescopes, microscopes, and cameras, where precise image formation is essential.

Enhancing Visibility in Vehicles: In vehicles, especially cars, the mirror equation is used to design rearview and side-view mirrors that provide drivers with a clear and accurate view of the traffic behind them.

Architectural and Interior Design: Architects and interior designers use the mirror equation to strategically place mirrors to achieve desired visual effects, such as making spaces appear larger or reflecting light to brighten a room.

Safety and Surveillance: Convex mirrors are often used for surveillance in stores and on roads to provide a wide field of view. The mirror equation helps in determining the placement and curvature of these mirrors for optimal visibility.

Medical Instruments: Some medical instruments, like endoscopes, use mirrors to allow doctors to see inside a patient’s body. The mirror equation helps in designing these instruments to provide clear images of internal organs.

Solved Examples

Example 1: An object is placed 25 cm in front of a concave mirror with a focal length of 10 cm. Determine the position and nature of the image formed.

Solution: We use the mirror equation:

\(\displaystyle\frac{1}{f} = \frac{1}{d_o} + \frac{1}{d_i}\)

Given: Focal length (f) = -10 cm (negative for concave mirrors); Object distance (d_o) = 25 cm

Substitute the values:

\(\displaystyle\frac{1}{-10} = \frac{1}{25} + \frac{1}{d_i}\)

Rearrange to solve for (d_i):

\(\displaystyle\frac{1}{d_i} = \frac{1}{-10} – \frac{1}{25}\)
\(\displaystyle\frac{1}{d_i} = -\frac{5}{50} – \frac{2}{50}\)
\(\displaystyle\frac{1}{d_i} = -\frac{7}{50}\)
\(\displaystyle d_i = -\frac{50}{7} \approx -7.14 \text{ cm}\)

The image is formed approximately 7.14 cm in front of the mirror, indicating that the image is real and inverted.

Example 2: An object is placed 20 cm in front of a convex mirror with a focal length of 15 cm. Determine the position and nature of the image formed.

Solution: We use the mirror equation:

\(\displaystyle\frac{1}{f} = \frac{1}{d_o} + \frac{1}{d_i}\)

Given: Focal length (f) = 15 cm (positive for convex mirrors); Object distance (d_o) = -20 cm (negative for convex mirrors)

Substitute the values:

\(\displaystyle\frac{1}{15} = \frac{1}{-20} + \frac{1}{d_i}\)

Rearrange to solve for (d_i):

\(\displaystyle\frac{1}{d_i} = \frac{1}{15} – \frac{1}{-20}\)

\(\displaystyle\frac{1}{d_i} = \frac{4}{60} + \frac{3}{60}\)

\(\displaystyle\frac{1}{d_i} = \frac{7}{60}\)

\(\displaystyle d_i = \frac{60}{7} \approx 8.57 \text{ cm}\)

The image is formed approximately 8.57 cm behind the mirror, indicating that the image is virtual, erect, and diminished.

Example 3: An object is placed 10 cm in front of a concave mirror and forms a real image 20 cm from the mirror. Determine the radius of curvature of the mirror.

Solution: We use the mirror equation:

\(\displaystyle\frac{1}{f} = \frac{1}{d_o} + \frac{1}{d_i}\)

Given: Object distance (d_o) = 10 cm; Image distance (d_i) = -20 cm (negative for real images)

Substitute the values:

\(\displaystyle\frac{1}{f} = \frac{1}{10} + \frac{1}{-20}

\)latex \displaystyle\frac{1}{f} = \frac{2}{20} – \frac{1}{20}

\(\displaystyle\frac{1}{f} = \frac{1}{20}

\)latex \displaystyle f = 20 \text{ cm}$

The radius of curvature (R) is given by:

\(\displaystyle R = 2f = 2 \times 20 = 40 \text{ cm}\)

The radius of curvature of the mirror is 40 cm.

FAQs