The concept of moment of inertia was first introduced by Leonhard Euler in 1765. It emerged from the study of rotational motion and the understanding of how mass contributes to resistance against changes in rotational speed.
The story of the moment of inertia begins with the renowned Swiss mathematician and physicist Leonhard Euler. In 1765, Euler introduced the term “momentum inertiae” in Latin, which translates to “moment of inertia” in his groundbreaking work “Theoria motus corporum solidorum seu rigidorum”¹. This was a significant advancement in the field of rotational dynamics.
Euler’s introduction of the moment of inertia was part of his development of what we now call Euler’s Laws of Motion for rigid bodies. These laws extended Sir Isaac Newton’s laws of motion, which were initially formulated for point masses, to rigid bodies—objects that do not deform under normal conditions.
The concept of moment of inertia was revolutionary because it provided a quantitative measure of the rotational inertia of a body—essentially, how much resistance a body offers to having its speed of rotation changed. Just as mass is a measure of an object’s resistance to changes in linear motion, the moment of inertia is a measure of an object’s resistance to changes in rotational motion.
Euler realized that just as force is needed to change an object’s linear velocity, torque is required to change an object’s angular velocity. The moment of inertia plays a crucial role in this relationship, as it determines the amount of torque needed for a desired angular acceleration around a rotational axis.
The moment of inertia is not just a single number; it depends on the body’s mass distribution and the axis chosen. For example, the same object can have different moments of inertia when rotating about different axes.
Euler’s work laid the foundation for modern engineering and physics, where the moment of inertia is essential for designing mechanical systems, understanding the motion of celestial bodies, and even in sports equipment to enhance performance.
What is Inertia?
“Inertia is the property of a body that resists any change to its state of rest or uniform motion.“
In simple terms, an object tends to “keep doing what it’s doing” – whether that’s staying still or moving at a constant velocity. Imagine you’re sitting in a car at a stoplight. When the light turns green, the car suddenly accelerates. You feel pushed back into your seat. That’s inertia in action. Inertia is the natural tendency of an object to resist changes in its state of motion or rest.
To put it simply, if something is at rest, like a book on a table, it wants to stay at rest. If you’ve ever tried to push a heavy piece of furniture, you know it takes a bit of effort to get it moving. That’s because the furniture has inertia—it doesn’t want to move from its state of rest.
Now, think about a ball rolling down a hill. Once it starts rolling, it wants to keep rolling unless something stops it, like friction or hitting a wall. That’s inertia too. The ball, once in motion, wants to stay in motion.
In physics terms, inertia is directly related to mass. The more mass an object has, the more inertia it has, and the harder it is to change its motion. That’s why a bowling ball is harder to push than a soccer ball.
So, when we talk about inertia in a physics class, we’re talking about this fundamental property of matter that resists changes in motion. It’s a concept that helps us understand why objects behave the way they do when forces are applied to them.
Inertia is a key part of Newton’s first law of motion, often called the law of inertia. It states that an object will stay at rest or move at a constant velocity unless acted upon by an external force. This law lays the foundation for classical mechanics and helps us predict the motion of objects in our everyday world.
What is a Moment of Inertia?
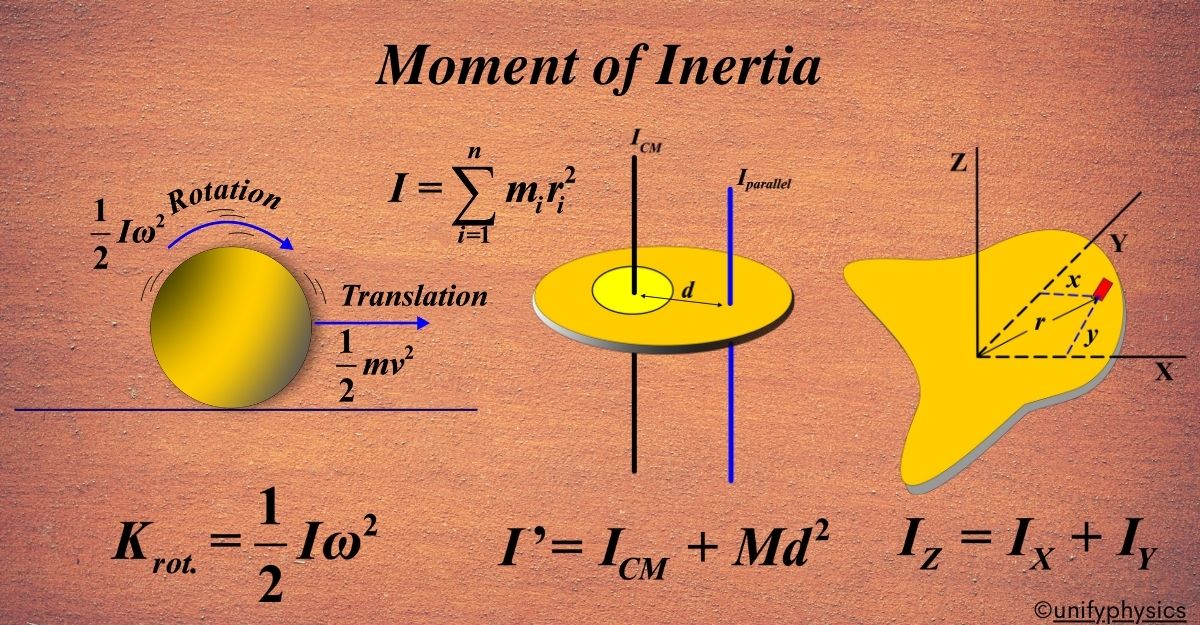
The Moment of Inertia (I) is a measure of an object’s resistance to changes in its rotational motion. It’s the rotational equivalent of mass in linear motion.
Think of the moment of inertia as a measure of an object’s ‘laziness’ when it comes to spinning around. Just like inertia is the resistance to change in motion, the moment of inertia is the resistance to change in rotation.
Here’s a simple way to picture it: Imagine you and a friend are on a playground merry-go-round. If you’re both sitting close to the center, it’s pretty easy to spin the merry-go-round. But if your friend moves to the edge, suddenly it’s a lot harder to make it spin. That’s because the moment of inertia has increased. The moment of inertia tells us how hard it is to start or stop an object spinning.
In physics terms, the moment of inertia depends on two things:
- The mass of the object: More mass means more ‘laziness’ or resistance to spinning.
- The distribution of that mass relative to the axis of rotation: The moment of inertia also depends on the axis around which the object is spinning. Mass further away from the axis increases the moment of inertia.
The formula for the moment of inertia is a bit like the recipe for this ‘laziness’. It’s usually written as:
\(\displaystyle I = \sum m_i r_i^2 \)
where (I) is the moment of inertia, (mi) is the mass of a small piece of the object, and (ri) is the distance from that piece to the axis of rotation. The sum is over all such pieces of the object. The unit of moment of inertia is kilogram square meter (kg·m²).
So, the further away the mass is from the center, the larger the value of (ri), and the larger the moment of inertia. That’s why your friend moving to the edge of the merry-go-round makes such a difference.
Moment of Inertia of a System of Particles
For a system of particles, the moment of inertia is the sum of the products of the mass of each particle and the square of its distance from the axis of rotation
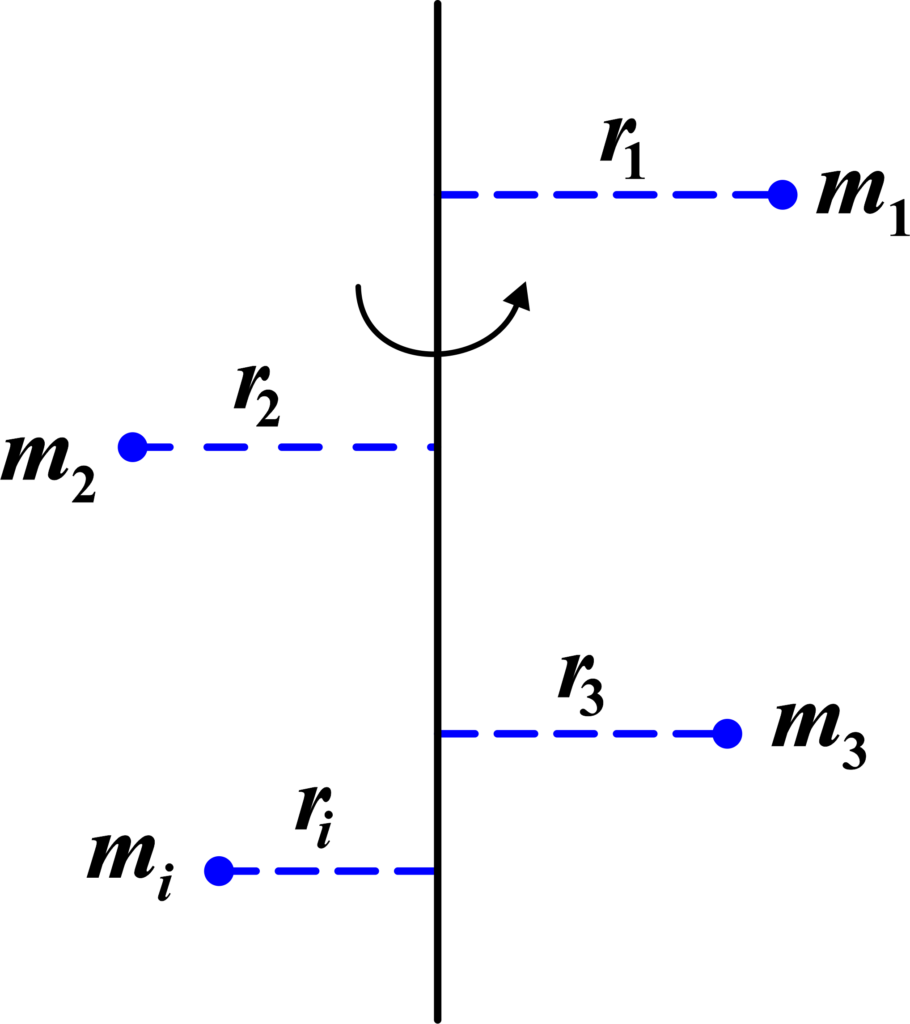
To start, let’s consider a system made up of particles. Each particle has a mass (mi) and is located at a distance (ri) from a fixed axis of rotation. The moment of inertia is a measure of how difficult it is to change the rotational motion of this system.
We look at each particle in the system individually. Let’s say we have (n) particles. Or each particle, we calculate its contribution to the moment of inertia.
This is done by multiplying the mass of the particle (mi) by the square of its distance from the axis (ri2).
Since the moment of inertia is a collective property, we add up the contributions from all the particles in the system. Putting it all together, the expression for the moment of inertia (I) of the system is the sum of all individual moments:
\(\displaystyle I = \sum_{i=1}^{n} m_i r_i^2 \)
This equation tells us that the moment of inertia is the sum of the products of the mass and the square of the distance from the axis for each particle in the system.
Example: Imagine you have a system with three particles;
- Particle 1 has a mass of (m1) and is (r1) meters from the axis.
- Particle 2 has a mass of (m2) and is (r2) meters from the axis.
- Particle 3 has a mass of (m3) and is (r3) meters from the axis.
The moment of inertia for this system would be:
\(\displaystyle I = m_1 r_1^2 + m_2 r_2^2 + m_3 r_3^2 \)
This formula can be used for any number of particles, and it shows how each particle’s position and mass affect the system’s overall resistance to rotational acceleration.
Moments of Inertia for Different Objects (Part- I)
Here are the expressions for the moment of inertia for some symmetric objects along with their rotation axis:
| Object | Axis | Expression of the Moment of Inertia |
|---|---|---|
| Hollow Cylinder (Thin-walled) | Central | \(\displaystyle I = m r^2 \) |
| Thin Ring | Diameter | \(\displaystyle I = \frac{1}{2} m r^2 \) |
| Annular Ring or Hollow Cylinder | Central | \(\displaystyle I = \frac{1}{2} m (r_{\text{outer}}^2 + r_{\text{inner}}^2) \) |
| Solid Cylinder | Central | \(\displaystyle I = \frac{1}{2} m r^2 \) |
| Uniform Disc | Diameter | \(\displaystyle I = \frac{1}{4} m r^2 \)$ |
| Hollow Sphere | Central | \(\displaystyle I = \frac{2}{3} m r^2 \) |
| Solid Sphere | Central | \(\displaystyle I = \frac{2}{5} m r^2 \) |
| Uniform Symmetric Spherical Shell | Central | \(\displaystyle I = \frac{2}{3} m r^2 \) |
| Uniform Plate or Rectangular Parallelepiped | Central | \(\displaystyle I = \frac{1}{12} m (l^2 + w^2) \) |
| Thin Rod | Central | \(\displaystyle I = \frac{1}{12} m l^2 \) |
| Thin Rod | At the End of Rod | \(\displaystyle I = \frac{1}{3} m l^2 \) |
In this table:
- (m) represents the mass of the object.
- (r) represents the radius, and it can be the inner, outer, or average radius depending on the object.
- (l) and (w) represent the length and width of the plate or parallelepiped, respectively.
Moment of Inertia Theorems
(i) Parallel Axis Theorem:
The parallel axis theorem states that the moment of inertia of a body about any axis is equal to the moment of inertia of the body about a parallel axis through its center of mass plus the product of the body’s mass and the square of the distance between the axes.
Imagine you have a spinning top. When it spins around its center, it has a certain resistance to change in its spinning speed.
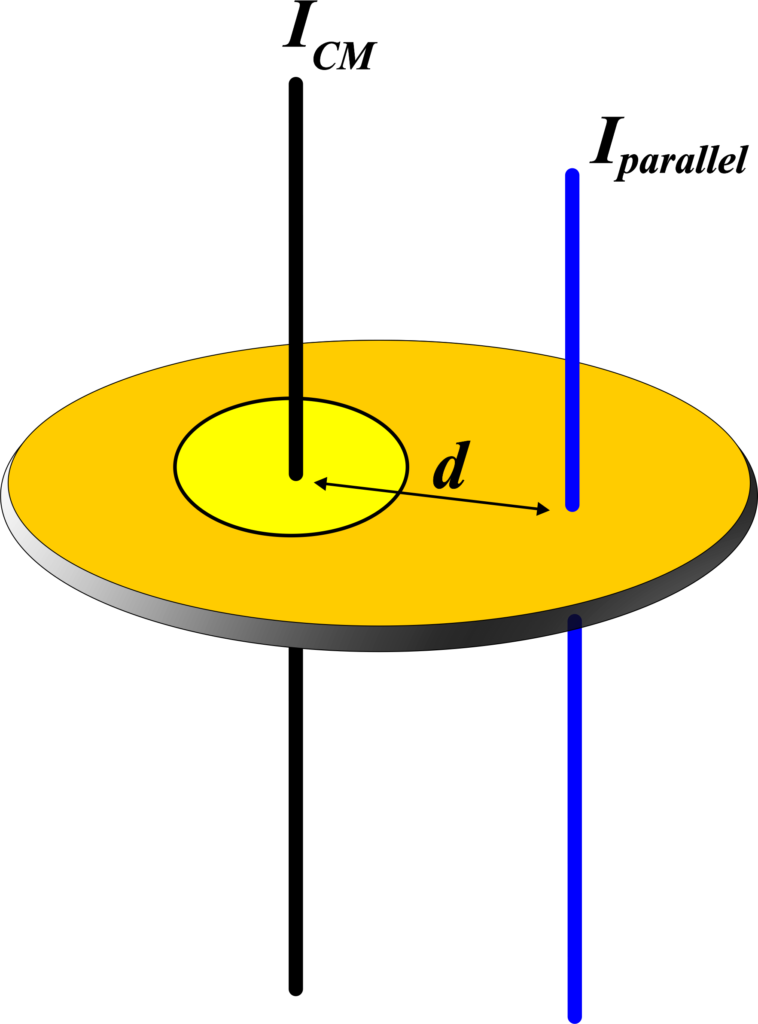
This resistance is due to its moment of inertia. Now, what if you could make the top spin around a point that’s not its center? The Parallel Axis Theorem helps us figure out the new moment of inertia in such cases.
The Parallel Axis Theorem allows us to find the moment of inertia of a body about any axis, given we know the moment of inertia about a parallel axis that passes through the center of mass and the distance between the two axes.
The moment of inertia (I) about an axis is the sum of the products of the mass of each particle (mi) and the square of its distance (ri) from the axis:
\(\displaystyle I = \sum m_i r_i^2 \)
Now, let’s consider a new axis that is parallel to the axis through the center of mass but at a distance (d) away from it.
For each particle, the distance from the new axis is ( ri‘ = ri + d). We square this to get:
\(\displaystyle r_i’^2 = (r_i + d)^2 = r_i^2 + 2r_id + d^2 \)
Now, we substitute (ri‘2) into the moment of inertia formula for the new axis (I’):
\(\displaystyle I’ = \sum m_i r_i’^2 = \sum m_i (r_i^2 + 2r_id + d^2) \)
When we expand this, we get three sums:
\(\displaystyle I’ = \sum m_i r_i^2 + \sum 2m_i r_i d + \sum m_i d^2 \)
The first sum, \(\displaystyle \sum m_i r_i^2 \), is just the moment of inertia about the center of mass (ICM). The middle term, \(\displaystyle \sum 2m_i r_i d \), becomes zero because, for any system of particles, the sum of the distances from the center of mass is zero by definition of the center of mass. The last term, \(\displaystyle\sum m_i d^2 \), can be factored out because (d) is constant for all particles:
\(\displaystyle \sum m_i d^2 = d^2 \sum m_i \)
The sum of the masses \(\displaystyle\sum m_i \) is just the total mass of the body (M). Putting it all together, we get:
\(\displaystyle I’ = I_{CM} + Md^2 \)
The moment of inertia about the new axis (I’) is equal to the moment of inertia about the center of mass (ICM) plus the product of the total mass (M) and the square of the distance (d2) between the two axes.
This theorem is very useful because it saves us from having to integrate to find the moment of inertia for every new axis we choose. Instead, we can use this shortcut as long as we know the moment of inertia about the center of mass and the distance to the new axis.
(ii) Perpendicular Axis Theorem:
The perpendicular axis theorem applies to planar objects only. It states that the moment of inertia about an axis perpendicular to the object’s plane is equal to the sum of the moments of inertia about two perpendicular axes that lie in the plane and intersect at a point where the perpendicular axis passes.
The perpendicular axis theorem applies to flat, two-dimensional objects.
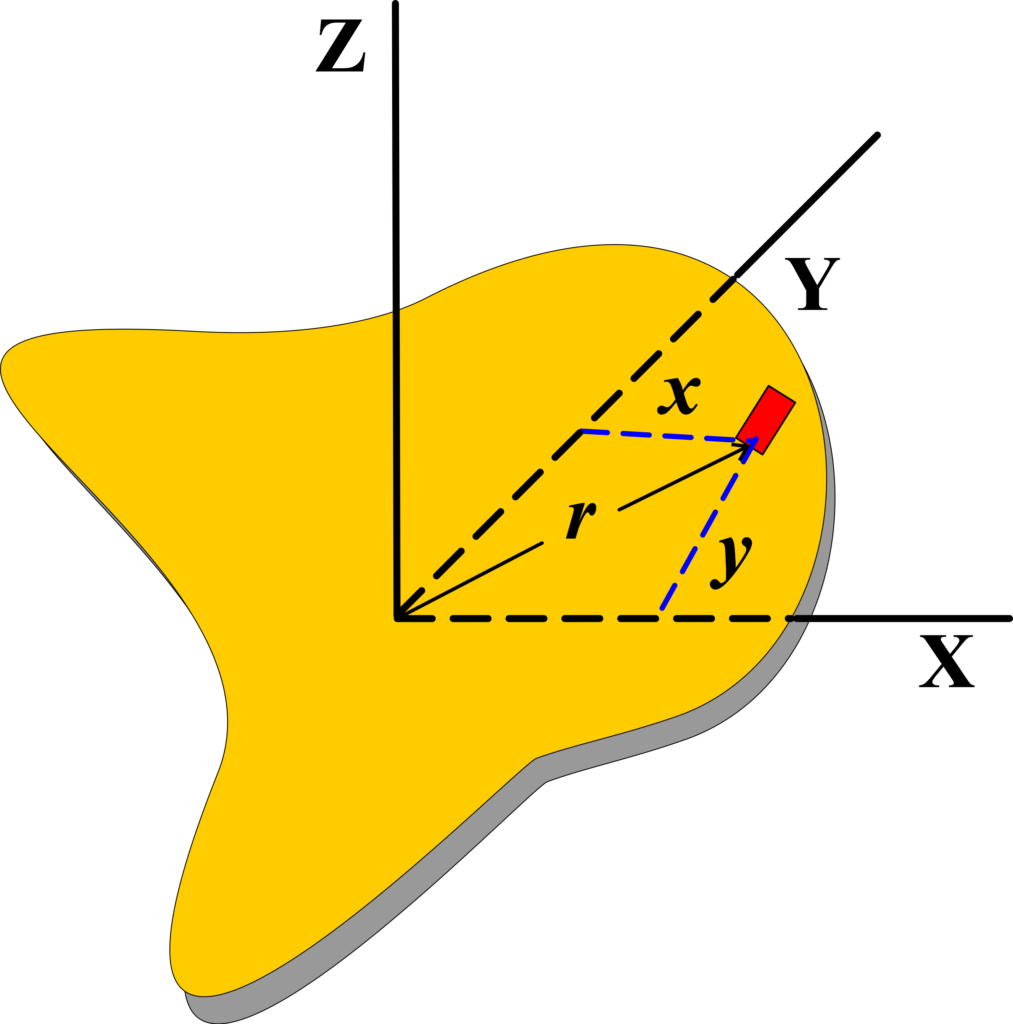
It states that the moment of inertia about an axis perpendicular to the plane of the object (Z-axis) is equal to the sum of the moments of inertia about two mutually perpendicular axes (X and Y axes) that lie in the plane of the object.
Take a flat, two-dimensional object that lies in the XY plane. Choose three mutually perpendicular axes: the X-axis, the Y-axis, and the Z-axis, where the Z-axis is perpendicular to the plane of the object.
Consider a small element of area (dA) on the object. Let the distances from this element to the X-axis and Y-axis be (y) and (x), respectively.
The moment of inertia of this small element about the Z-axis is given by \(\displaystyle dI_Z = r^2 dA \), where (r) is the distance from the element to the Z-axis. Since the object lies in the XY plane, (r2 = x2 + y2).
To find the total moment of inertia about the Z-axis, we integrate over the entire object:
\(\displaystyle I_Z = \int r^2 dA = \int (x^2 + y^2) dA \)
This integral can be separated into two parts, one for each axis in the plane:
\(\displaystyle I_Z = \int x^2 dA + \int y^2 dA \)
The integrals \(\displaystyle\int x^2 dA \) and \(\displaystyle\int y^2 dA \) represent the moments of inertia about the X-axis (IX) and Y-axis (IY), respectively.
By combining the moments of inertia about the X and Y axes, we get the moment of inertia about the Z-axis:
\(\displaystyle I_Z = I_X + I_Y \)
The moment of inertia about the Z-axis (perpendicular to the plane) is the sum of the moments of inertia about the X-axis and Y-axis (both in the plane). This theorem is particularly useful because it simplifies the moment of inertia calculation for complex shapes by breaking them down into simpler components.
Kinetic Energy in Rotational Motion
When we think of kinetic energy, we usually think of the energy an object has because it’s moving in a straight line. This is called translational kinetic energy. But objects can also have kinetic energy because they’re spinning or rotating, and this is what we call rotational kinetic energy.
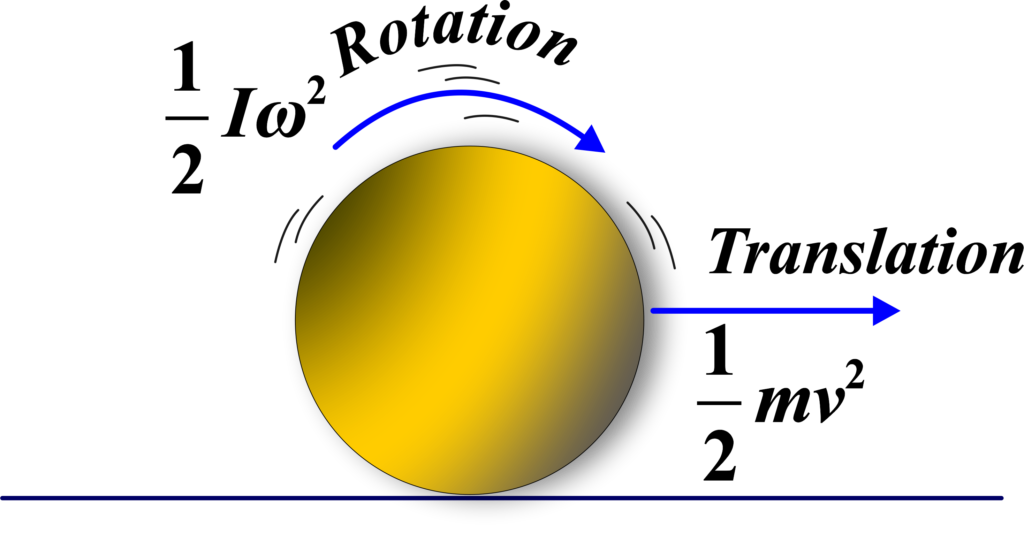
When an object rotates, each particle in the object has kinetic energy due to its motion. The total kinetic energy of the rotating object is the sum of the kinetic energies of all its particles. Imagine an object rotating about an axis. Each particle in the object moves in a circle with a certain speed that depends on its distance from the axis of rotation.
The kinetic energy (KE) of a single particle with mass (m) moving at velocity (v) is given by:
\(\displaystyle KE = \frac{1}{2}mv^2 \)
For rotational motion, the linear velocity (v) of a particle at a distance (r) from the axis of rotation is related to the angular velocity (ω) by:
\(\displaystyle v = \omega r \)
Replace the linear velocity with the expression involving angular velocity:
\(\displaystyle KE = \frac{1}{2}m(\omega r)^2 \)
When you expand the expression, you get:
\(\displaystyle KE = \frac{1}{2}m\omega^2r^2 \)
The term (mr2) is the moment of inertia (I) of the particle about the axis of rotation. So for one particle, the kinetic energy becomes:
\(\displaystyle KE = \frac{1}{2}I\omega^2 \)
For the entire object, the total kinetic energy is the sum of the kinetic energies of all particles. If the object is rigid and all particles rotate with the same angular velocity, we can sum up their moments of inertia:
\(\displaystyle K_{\text{total}} = \frac{1}{2}(I_1 + I_2 + \ldots + I_n)\omega^2 \)
The sum of all individual moments of inertia \(\displaystyle ( I_1 + I_2 + \ldots + I_n \)) is the total moment of inertia (I) of the object. The final expression for the kinetic energy of a rotating object is:
\(\displaystyle K_{\text{rot}} = \frac{1}{2}I\omega^2 \)
This equation tells us that the rotational kinetic energy depends on the moment of inertia and the square of the angular velocity. It’s similar to the expression for translational kinetic energy but involves rotational quantities instead.
Example: A spinning top or a wheel rolling down the street. While it’s spinning or rolling, it has energy due to its rotation. This energy is what we call rotational kinetic energy. If you have a wheel spinning faster (higher (ω), or if the mass of the wheel is further from the center (higher (I), the wheel will have more rotational kinetic energy.
Rotational kinetic energy is part of an object’s total kinetic energy. For example, a rolling ball has both translational kinetic energy (because it’s moving forward) and rotational kinetic energy (because it’s spinning).
Also Read: Rigid Body
Radius of Gyration
The radius of gyration (k) is the distance from the axis of rotation at which the entire mass of the body could be concentrated without changing its moment of inertia.
The radius of gyration (k) is a measure that gives us an equivalent distance at which the entire mass of an object can be assumed to be concentrated, such that the moment of inertia remains the same as if the mass were spread out.
The moment of inertia (I) for a system of particles is given by the sum of the products of the mass of each particle (mi) and the square of its distance (ri) from the axis of rotation:
\(\displaystyle I = \sum m_i r_i^2 \)
Let the total mass of the system be (M), which is the sum of the masses of all the particles:
\(\displaystyle M = \sum m_i \)
We define the radius of gyration (k) such that the moment of inertia can also be expressed as:
\(\displaystyle I = Mk^2 \)
Now, we set the two expressions for the moment of inertia equal to each other:
\(\displaystyle \sum m_i r_i^2 = Mk^2 \)
To find the radius of gyration, we solve for (k):
\(\displaystyle k^2 = \frac{\sum m_i r_i^2}{M} \)
Taking the square root of both sides, we get:
\(\displaystyle k = \sqrt{\frac{\sum m_i r_i^2}{M}} \)
And there we have it! The radius of gyration (k) is the square root of the sum of the products of the mass of each particle and the square of its distance from the axis of rotation, all divided by the total mass of the system.
This derived expression tells us that the radius of gyration is essentially the root-mean-square distance of the system’s mass distribution from the axis of rotation.
If you know the moment of inertia and the mass of an object, you can calculate this special distance, the radius of gyration. It’s a useful way to simplify problems in rotational dynamics because it allows us to treat complex objects as if all their mass were located at a single point.
For example, if you’re designing a flywheel or a roller coaster loop, knowing the radius of gyration helps you predict how these objects will behave when they spin or rotate.
Moments of Inertia for Different Objects (Part- II)
| Object | Axis | Expression of the Moment of Inertia |
|---|---|---|
| Rectangular Plate | Through the center and perpendicular to the plane | $$ I = \frac{1}{12} m (l^2 + w^2) $$ |
| Disc | About the disc’s geometric axis | $$ I = \frac{1}{2} m r^2 $$ |
| Rod | Axis perpendicular to the length of the rod and passing through its center of gravity | $$ I = \frac{1}{12} m l^2 $$ |
| Circle | Axis passing through perpendicularly to the center of the ring | $$ I = m r^2 $$ |
| Sphere | About its diameter | $$ I = \frac{2}{5} m r^2 $$ |
| Solid Cylinder | About the central axis | $$ I = \frac{1}{2} m r^2 $$ |
| Hollow Cylinder | About the central axis | $$ I = m r^2 $$ |
In these formulas:
- (m) represents the mass of the object.
- (r) represents the object’s radius (for the disc, circle, sphere, and cylinders).
- (l) and (w) represents the length and width of the rectangular plate, respectively.
Factors Affecting Moment of Inertia
The moment of inertia is a property of a body that measures its resistance to changes in rotational motion. It’s like how mass measures resistance to changes in linear motion. But instead of just depending on mass, the moment of inertia depends on a few more factors:
- Mass of the Body: The greater the mass, the greater the moment of inertia. It’s like trying to push a heavy door versus a light one; the heavier door (with more mass) is harder to start or stop spinning.
- Shape and Size of the Body: The shape and size determine how the mass is distributed relative to the axis of rotation. For example, a long, thin rod has a different moment of inertia when spun around its end compared to when spun around its center.
- Distribution of Mass Relative to the Axis: This is where the radius comes into play. Mass that’s further from the axis increases the moment of inertia because it has a larger ‘lever arm’ to resist rotational changes. It’s like holding a hammer by the end of the handle versus near the head when you want to swing it.
- Density of the Material: Denser materials pack more mass into the same volume, which can affect the moment of inertia. A solid steel cylinder will have a different moment of inertia than a hollow aluminum one, even if they’re the same size.
- Axis of Rotation: The position and orientation of the axis of rotation also affect the moment of inertia. An object can have multiple moments of inertia depending on the axis about which it’s rotating.
Moments of Inertia for Different Objects (Part- III)
| Object | Axis | Expression of the Moment of Inertia |
|---|---|---|
| Solid Sphere | About its diameter | $$ I = \frac{2}{5} m r^2 $$ |
| Hollow Sphere | About any diameter | $$ I = \frac{2}{3} m r^2 $$ |
| Ring (center) | About the axis through the center, perpendicular to the plane | $$ I = m r^2 $$ |
| Ring (diameter) | About the axis through the diameter | $$ I = \frac{1}{2} m r^2 $$ |
| Square | About an axis through the center, perpendicular to the plane | $$ I = \frac{1}{6} m a^2 $$ |
| Square Plate | About an axis through the center, perpendicular to the plane | $$ I = \frac{1}{6} M l^2 $$ |
| Triangle (centroid) | About an axis through the centroid, perpendicular to the plane | $$ I = \frac{1}{18} m h^2 $$ |
| Triangle (base) | About an axis through the base, parallel to the base | $$ I = \frac{1}{36} m h^2 $$ |
| Triangle (perpendicular to base) | About an axis perpendicular to the base, passing through the base | $$ I = \frac{1}{12} m h^2 $$ |
| Solid Box | About an axis through the center, perpendicular to one face | $$ I = \frac{1}{12} m (h^2 + w^2) $$ |
In these formulas:
- (r) represents the radius (for the sphere, hollow sphere, and rings).
- (a) represents the side length of the square.
- (l) represents the side length of the square plate.
- (h) represents the height of the triangle.
- (w) represents the width of the solid box.
Application of Moment of Inertia
The Moment of Inertia is a fundamental concept in physics that has a wide range of applications, especially in anything that involves rotation.
- Engineering and Machinery: In mechanical engineering, the moment of inertia is crucial for designing gears, engines, and machinery parts that rotate. It helps engineers ensure that these components can rotate smoothly and handle the stresses of motion.
- Sports Equipment: The design of sports equipment like discuses, javelins, ice skates, and even golf clubs takes into account the moment of inertia to optimize performance. For example, a bat with a lower moment of inertia is easier to swing, which can help a batter hit a ball further.
- Vehicle Dynamics: The moment of inertia affects how vehicles handle turns and how stable they are at different speeds. Car wheels, for instance, are designed with a specific moment of inertia to provide a balance between acceleration and traction.
- Astronomy: In astronomy, the moment of inertia of celestial bodies like planets and stars can give us insights into their internal structure and how they will evolve over time. It also plays a role in the dynamics of orbiting systems.
- Construction: When constructing buildings and bridges, the moment of inertia is important for understanding how these structures will respond to forces like wind and earthquakes. It helps in designing them to be both stable and flexible.
- Consumer Electronics: In devices like computer hard drives and CD players, the moment of inertia of the spinning disks is optimized for quick and accurate reading and writing of data.
- Robotics: Robots often have moving parts that rotate. The moment of inertia is used to control these movements precisely, which is essential for robots that perform delicate tasks or need to move efficiently.
- Energy Storage: Flywheels are devices that store energy as rotational motion. Their moment of inertia is key to how much energy they can store and how quickly they can release it.
In all these applications, the moment of inertia helps us predict and control rotational motion, making it an indispensable tool in both theoretical physics and practical engineering.
FAQs
What is the moment of inertia in physics, and how is it different from mass?
The moment of inertia is a measure of an object’s resistance to changes in its rotational motion. It is analogous to mass in linear motion, as it quantifies how much mass is distributed around an axis of rotation. However, while mass measures an object’s resistance to linear acceleration, moment of inertia measures its resistance to rotational acceleration.
How is the moment of inertia of a system of particles calculated?
The moment of inertia of a system of particles is calculated by summing the products of the mass of each particle and the square of its distance from the axis of rotation. Mathematically, it is expressed as ( I = ∑ mi ri2 ).
What is the Parallel Axis Theorem, and how is it used to calculate the moment of inertia?
The Parallel Axis Theorem states that the moment of inertia of an object about an axis parallel to its center of mass axis is equal to the sum of its moment of inertia about the center of mass axis and the product of its total mass and the square of the distance between the two axes. Mathematically, it is expressed as ( I = Icm+ md2).
How does the Perpendicular Axis Theorem relate to moment of inertia calculations?
The Perpendicular Axis Theorem states that the moment of inertia of a planar lamina about an axis perpendicular to its plane is equal to the sum of its moments of inertia about two perpendicular axes lying in the plane of the lamina and intersecting at the point where the perpendicular axis passes through. Mathematically, it is expressed as ( Iz = Ix + Iy ).
How is kinetic energy related to rotational motion, and how is it calculated?
The kinetic energy in rotational motion is the energy associated with the rotational motion of an object. It depends on both the moment of inertia of the object and its angular velocity. Mathematically, the kinetic energy ( K ) in rotational motion is calculated as \(\displaystyle K = \frac{1}{2} I \omega^2 \).
What is the radius of gyration, and how is it related to moment of inertia?
The radius of gyration is a measure of how far the mass of an object is distributed from its axis of rotation. It is the distance from the axis of rotation at which the entire mass of the object could be concentrated to give the same moment of inertia as the actual distribution of mass. Mathematically, it is expressed as \(\displaystyle k = \sqrt{\frac{I}{m}} \).
Can you provide examples illustrating the concepts of moment of inertia and kinetic energy in rotational motion?
Examples include a rotating bicycle wheel and a spinning figure skater. In both cases, the distribution of mass and the speed of rotation affect both the moment of inertia and the kinetic energy of the system. The moment of inertia determines how easily the object can be accelerated or decelerated, while the kinetic energy reflects the amount of energy associated with its rotational motion.