The concept of motion in a plane, or two-dimensional motion, has been a subject of fascination and study for centuries. It encompasses the movement of objects in a plane, considering both the x-axis and y-axis, unlike one-dimensional motion which only considers a single line of action.
In ancient times, Aristotle’s view dominated, suggesting that objects in the heavens moved in perfect circles and that earthly objects sought their natural place, moving straight up or down. The real breakthrough came during the Renaissance when Galileo Galilei conducted experiments and concluded that projectiles move in a curved path, which we now know as a parabola. He separated the motion into two components: horizontal motion, which was uniform, and vertical motion, which was uniformly accelerated due to gravity.
Later, Sir Isaac Newton’s laws of motion and universal gravitation provided a comprehensive framework for understanding motion in a plane. Newton’s laws described how forces affect motion, leading to the development of classical mechanics. In the 18th century, mathematicians like Euler and Lagrange developed analytical mechanics, which used calculus to further refine the understanding of motion. The introduction of vector analysis in the 19th century by Josiah Willard Gibbs and Oliver Heaviside simplified the representation and analysis of motion in a plane.
The 20th century brought about quantum mechanics and Einstein’s theory of relativity, which, while primarily concerned with motion at very small scales and high speeds, respectively, also contributed to the overall understanding of motion.
Position Vector and Displacement
Position Vector: When we talk about motion in a plane, we’re referring to movement that occurs in two dimensions. This is the kind of motion that happens on a flat surface, like a piece of paper, where you can move up, down, left, or right. To describe this motion, we use something called a position vector.
What is a Position Vector?
- A position vector is a mathematical tool that we use to specify the exact location of a point in a plane.
- Think of it as an arrow that starts from a fixed point, usually called the origin, and points directly to the object’s location.
- It’s like using a map where you draw a line from a landmark to your current spot to show where you are.
How Do We Represent It?: In two dimensions, we represent the position vector as \(\displaystyle\vec{r} = x\hat{i} + y\hat{j}\).
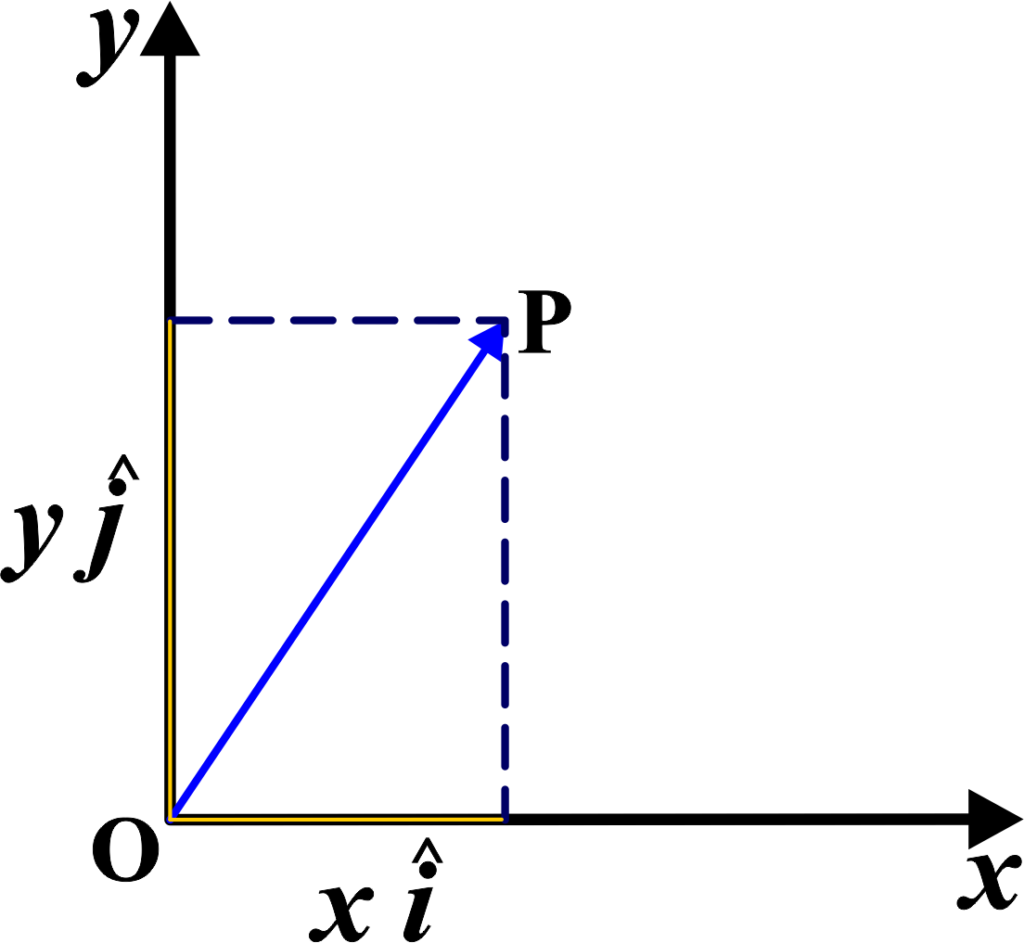
- Here, (x) and (y) are the coordinates on the plane, telling us how far along the x-axis and y-axis the object is.
- The symbols \(\displaystyle\hat{i}\) and \(\displaystyle\hat{j}\) are unit vectors. They’re like signposts that tell us the direction along the x-axis and y-axis, respectively.
The position vector is crucial because it gives us a complete description of where an object is at any given moment. It’s not enough to say something is 5 meters away; we need to know in which direction. The position vector solves this by including both the distance and the direction.
As an object moves, its position vector changes, which tells us it’s moving. By looking at how the position vector changes over time, we can understand the object’s motion, like how fast it’s going and where it’s heading.
Example
- Imagine you’re flying a drone in a park. The position vector tells you exactly where the drone is relative to your starting point.
- If the drone moves, the position vector updates, giving you a new location. This helps you track the drone’s path as it flies around.
Displacement: When we talk about motion in a plane, we’re referring to movement across a two-dimensional space, like a chessboard or a football field. To describe this movement, we use something called a displacement vector.
What is a Displacement Vector?
- A displacement vector represents the change in position of an object.
- It’s a straight line drawn from the starting point to the final point of an object’s journey.
- Unlike the position vector, which tells us where an object is, the displacement vector shows us how far and in which direction the object has moved.
How Do We Represent It?: Mathematically, if an object moves from point P with position vector \(\displaystyle\vec{r}\) to point P’ with position vector \(\displaystyle\overrightarrow{r}’\), the displacement vector \(\displaystyle \Delta \overrightarrow{r}\) is given by \(\displaystyle \Delta \overrightarrow{r}=\overrightarrow{r}’-\overrightarrow{r}\)
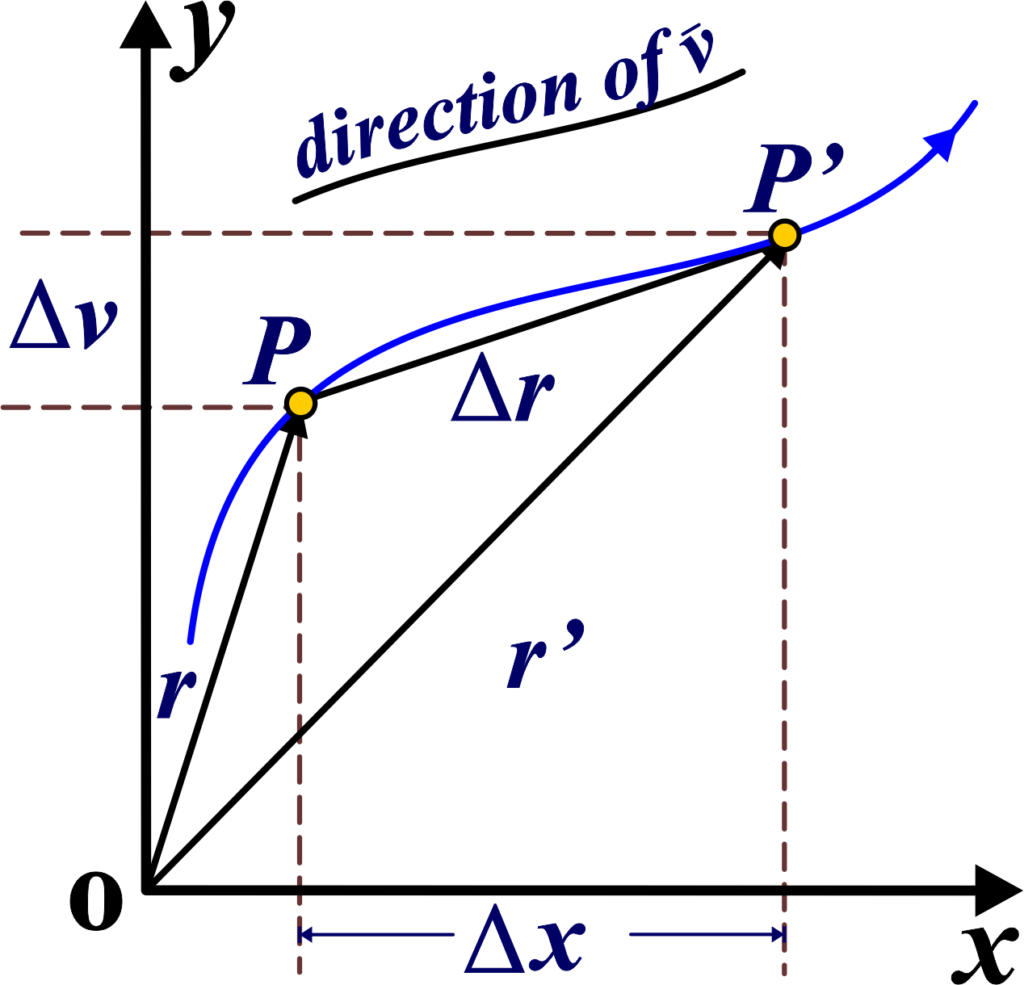
In two dimensions, if point P has coordinates (x, y) and point P’ has coordinates (x’, y’), the displacement vector \(\displaystyle\vec{r}\) can be represented as
\(\displaystyle \begin{array}{l}\Delta \overrightarrow{r}=\left( {x’\widehat{i}+y’\widehat{j}} \right)-\left( {x\widehat{i}+y\widehat{j}} \right)\end{array}\)
\(\displaystyle \Delta \overrightarrow{r}=\widehat{i}\Delta x+\widehat{j}\Delta y\)
The displacement vector is essential because it tells us the shortest path between two points. It’s not just about how much ground an object has covered; it’s about the object’s overall change in position.
Example:
- Imagine you’re at home and you walk to a friend’s house, then to the store, and finally back home. Your walking path might look like a big loop.
- The displacement vector, however, would be zero because you ended up where you started. It doesn’t matter how far you walk; what matters is your change in position.
The displacement vector is all about where you started, where you ended up, and the straight line between these two points!
Also Read: Relative Velocity
Velocity
Velocity is the rate of change of the position vector with respect to time. It is a vector quantity, meaning it has both magnitude and direction. When we talk about motion in a plane, we mean movement in a two-dimensional space, like a bird flying in the sky or a car moving through city streets. To describe this motion, we use the concept of velocity.
What is Velocity?
- Velocity is a vector quantity that tells us how fast an object is moving and in which direction.
- It’s like speed with a purpose; not only do we care about how fast something is going, but also where it’s headed.
Mathematically, velocity is represented as
\(\displaystyle\vec{v} = \frac{d\vec{r}}{dt}\),
where \(\displaystyle\vec{v}\) is the velocity vector, and \(\displaystyle\vec{r}\) is the position vector. The average velocity \(\displaystyle \overline{v}\) of an object is the ratio of the displacement and the corresponding time interval is,
\(\displaystyle \overline{v}=\frac{{\Delta r}}{{\Delta t}}=\frac{{\Delta x\widehat{i}+\Delta y\widehat{j}}}{{\Delta t}}=\widehat{i}\frac{{\Delta x}}{{\Delta t}}+\widehat{j}\frac{{\Delta y}}{{\Delta t}}\)
OR,
\(\displaystyle\overline{v}={{\overline{v}}_{x}}\widehat{i}+{{\overline{v}}_{y}}\widehat{j}\)
Velocity is crucial because it helps us predict where an object will be in the future based on its current speed and direction. It’s not just about getting from point P to point P’; it’s about knowing the path you’ll take to get there.
The velocity (instantaneous velocity) is given by the limiting value of the average velocity as the time interval approaches zero, and then
\(\displaystyle \overrightarrow{v}=\underset{{\Delta t\to 0}}{\mathop{{\lim }}}\,\frac{{\Delta r}}{{\Delta t}}=\frac{{d\overrightarrow{r}}}{{dt}}\)
So, at any spot along the path of an object, the direction it’s moving in is the same as the direction of its velocity. This direction is like a tangent to the path at that point.
\(\displaystyle v={{v}{x}}\widehat{i}+{{v}{y}}\widehat{j}\)
Where, \(\displaystyle {{v}_{x}}=\frac{{dx}}{{dt}},{{v}_{y}}=\frac{{dy}}{{dt}}\)
If we have equations that tell us how the x and y coordinates change over time, we can use these equations to figure out how fast the object is moving in the x (horizontal) and y (vertical) directions, which we call (vx) and (vy) respectively. Then, to find how fast the object is moving overall, we calculate the magnitude of the velocity vector.
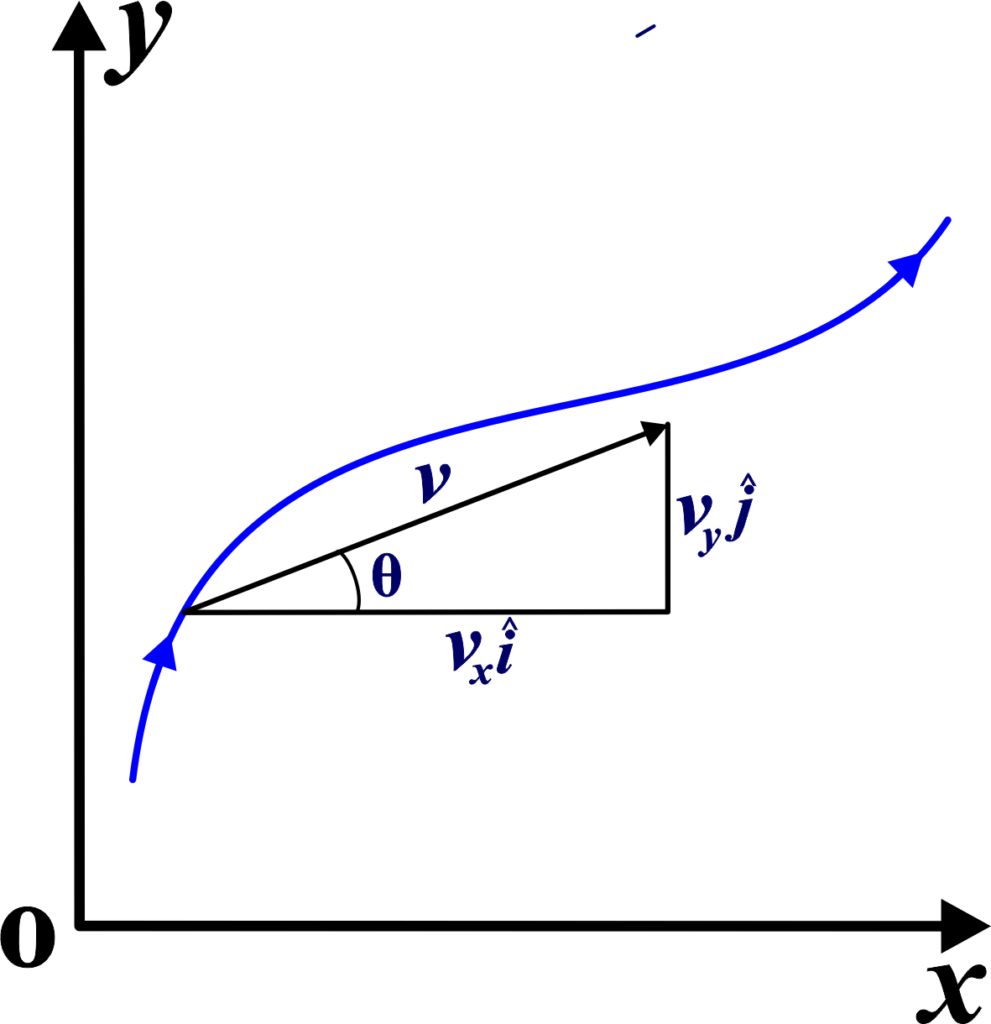
Then, to find how fast the object is moving overall, we calculate the magnitude of the velocity vector.
\(\displaystyle v=\sqrt{{v_{x}^{2}+v_{y}^{2}}}\)
and the direction of v is given by the angle θ
\(\displaystyle \tan \theta =\frac{{{{v}_{y}}}}{{{{v}_{x}}}},\theta ={{\tan }^{{-1}}}\left( {\frac{{{{v}_{y}}}}{{{{v}_{x}}}}} \right)\)
Therefore, the direction of velocity at any point on the path of an object is tangential to the path at that point and is in the direction of motion.
Acceleration
Acceleration is the rate of change of velocity with respect to time. It is also a vector quantity and is given by
\(\displaystyle\vec{a} = \frac{d\vec{v}}{dt}\).
where \(\displaystyle\vec{a}\) is the acceleration vector, \(\displaystyle\vec{v}\) is the velocity vector, and (dt) represents a small interval of time. This means acceleration can occur due to a change in the magnitude of velocity (speeding up or slowing down) a change in its direction, or both.
The average acceleration a of an object for a time interval Δt moving in x-y plane is the change in velocity divided by the time interval be,
\(\displaystyle \overline{a}=\frac{{\Delta v}}{{\Delta t}}=\frac{{\Delta \left( {v\widehat{i}+v\widehat{j}} \right)}}{{\Delta t}}=\frac{{\Delta {{v}_{x}}}}{{\Delta t}}\widehat{i}+\frac{{\Delta {{v}_{y}}}}{{\Delta t}}\widehat{j}\)
Or,
\(\displaystyle \overline{a}={{a}{x}}\widehat{i}+{{a}{y}}\widehat{j}\)
Where, \(\displaystyle {{a}_{x}}=\frac{{d{{v}_{x}}}}{{dt}},{{a}_{y}}=\frac{{d{{v}_{y}}}}{{dt}}\)
The acceleration (instantaneous acceleration) is the limiting value of the average acceleration as the time interval approaches zero,
\(\displaystyle a=\underset{{\Delta t\to 0}}{\mathop{{\lim }}}\,\frac{{\Delta v}}{{\Delta t}}\)
When an object moves in a straight line, its speed and how fast it’s speeding up or slowing down are always in the same direction or exactly opposite directions. But if it’s moving in two or three directions, its speed and how fast it’s speeding up or slowing down can be at any angle between 0 and 180 degrees apart.
Example: Imagine you’re on a merry-go-round. As it starts spinning, you feel a push—that’s acceleration. Even if the merry-go-round spins at a constant speed, if you move towards or away from the center, you’ll feel acceleration because your direction is changing.
Solved Examples
Problem 1: A particle moves from point (A) with coordinates ((2, 3)) to point (B) with coordinates ((5, 7)). Calculate the displacement vector.
Solution: Displacement vector (\(\displaystyle\mathbf{r}\)) is given by:
\(\displaystyle \mathbf{r} = \mathbf{r}_B – \mathbf{r}_A \)
Given: \(\displaystyle \mathbf{r}_A = (2, 3) ; \)latex \displaystyle \mathbf{r}_B = (5, 7) $
\(\displaystyle \mathbf{r} = (5 – 2, 7 – 3) \)
\(\displaystyle \mathbf{r} = (3, 4) \)
The displacement vector is ((3, 4)).
Problem 2: A particle’s position vector is given by (\(\displaystyle\mathbf{r}(t) = (3t^2, 2t + 1) \)). Find its velocity vector at (t = 2) seconds.
Solution: Velocity vector (\(\displaystyle\mathbf{v}(t)\)) is given by the derivative of the position vector with respect to time:
\(\displaystyle \mathbf{v}(t) = \frac{d\mathbf{r}(t)}{dt} \)
Given:\(\displaystyle \mathbf{r}(t) = (3t^2, 2t + 1) \)
\(\displaystyle \mathbf{v}(t) = \left( \frac{d}{dt} (3t^2), \frac{d}{dt} (2t + 1) \right) \)
\(\displaystyle \mathbf{v}(t) = (6t, 2) \)
At (t = 2):
\(\displaystyle \mathbf{v}(2) = (6 \times 2, 2) \)
\(\displaystyle \mathbf{v}(2) = (12, 2) \)
The velocity vector at (t = 2) seconds is ((12, 2)).
Problem 3: A particle’s velocity vector is given by (\(\displaystyle\mathbf{v}(t) = (4t, 3t^2)\)). Find its acceleration vector at (t = 1) second.
Solution: Acceleration vector (\(\displaystyle\mathbf{a}(t)\)) is given by the derivative of the velocity vector with respect to time:
\(\displaystyle \mathbf{a}(t) = \frac{d\mathbf{v}(t)}{dt} \)
Given:\(\displaystyle \mathbf{v}(t) = (4t, 3t^2) \)
\(\displaystyle \mathbf{a}(t) = \left( \frac{d}{dt} (4t), \frac{d}{dt} (3t^2) \right) \)
\(\displaystyle \mathbf{a}(t) = (4, 6t) \)
At (t = 1):
\(\displaystyle \mathbf{a}(1) = (4, 6 \times 1) \)
\(\displaystyle \mathbf{a}(1) = (4, 6) \)
The acceleration vector at ( t = 1 ) second is ( (4, 6) ).
Problem 4: A particle is moving in a circle of radius (5 m) with a constant speed of (10 m/s). Calculate the magnitude of its acceleration.
Solution: For uniform circular motion, the acceleration is centripetal and is given by:
\(\displaystyle a = \frac{v^2}{r} \)
Given: v = 10 m/s; r = 5 m.
\(\displaystyle a = \frac{10^2}{5} \)
\(\displaystyle a = \frac{100}{5} \)
\(\displaystyle a = 20 \, \text{m/s}^2 \)
The magnitude of the acceleration is (20 m/s2).
Problem 5: A projectile is launched with an initial velocity of (50 m/s) at an angle of (45∘) to the horizontal. Calculate the time of flight and range of the projectile.
Solution: Time of flight:
\(\displaystyle T = \frac{2u \sin \theta}{g} \)
Range:\(\displaystyle R = \frac{u^2 \sin 2\theta}{g} \)
Given: u = 50 m/s; θ = 45∘; g = 9.8 m/s2
Time of flight:
\(\displaystyle T = \frac{2 \times 50 \times \sin 45^\circ}{9.8} \)
\(\displaystyle \sin 45^\circ = \frac{\sqrt{2}}{2} \)
\(\displaystyle T = \frac{2 \times 50 \times \frac{\sqrt{2}}{2}}{9.8} \)
\(\displaystyle T = \frac{50 \sqrt{2}}{9.8} \)
\(\displaystyle T \approx 7.21 \, \text{s} \)
Range:
\(\displaystyle R = \frac{50^2 \sin 90^\circ}{9.8} \)
\(\displaystyle \sin 90^\circ = 1 \)
\(\displaystyle R = \frac{2500}{9.8} \)
\(\displaystyle R \approx 255.1 \, \text{m} \)
The time of flight is approximately (7.21) seconds and the range is approximately (255.1) meters.
Problem 6: A boat is moving with a velocity of (4 m/s) due east in a river flowing with a velocity of (3 m/s) due north. Calculate the resultant velocity of the boat relative to the ground.
Solution: The resultant velocity vector (\(\displaystyle\mathbf{v_r}\)) is given by:
\(\displaystyle \mathbf{v_r} = \mathbf{v_b} + \mathbf{v_r} \)
Given:\(\displaystyle \mathbf{v_b} = (4, 0) \, \text{m/s} \); \(\displaystyle \mathbf{v_r} = (0, 3) \, \text{m/s} \)
\(\displaystyle \mathbf{v_r} = (4, 0) + (0, 3) \)
\(\displaystyle \mathbf{v_r} = (4, 3) \)
Magnitude of the resultant velocity:
\(\displaystyle v_r = \sqrt{4^2 + 3^2} \)
\(\displaystyle v_r = \sqrt{16 + 9} \)
\(\displaystyle v_r = \sqrt{25} \)
\(\displaystyle v_r = 5 \, \text{m/s} \)
Direction (angle (θ) with the east direction):
\(\displaystyle \tan \theta = \frac{3}{4} \)
\(\displaystyle \theta = \tan^{-1} \left( \frac{3}{4} \right) \)
\(\displaystyle \theta \approx 36.87^\circ \)
The resultant velocity of the boat relative to the ground is (5 m/s) at an angle of (36.87∘) north of east.
FAQs
What is ‘Motion in a Plane’?
Motion in a plane refers to the movement of an object in two dimensions, typically described using the x and y axes. It involves analyzing the object’s position, velocity, and acceleration in a two-dimensional space.
Can an object have zero acceleration in ‘Motion in a Plane’?
Yes, an object can have zero acceleration in motion in a plane if it’s moving at a constant velocity or is at rest, meaning there’s no change in its velocity.
How do vectors play a role in describing ‘Motion in a Plane’?
Vectors are essential in describing motion in a plane as they provide both magnitude and direction for quantities like displacement, velocity, and acceleration, which are crucial for analyzing an object’s motion.
What is the difference between speed and velocity in ‘Motion in a Plane’?
Speed is a scalar quantity that refers only to how fast an object is moving, while velocity is a vector quantity that describes both the speed and direction of the object’s motion.
How do we calculate the resultant velocity of an object in ‘Motion in a Plane’?
The resultant velocity can be calculated using vector addition, where the individual velocity components along the x and y axes are combined to give the overall velocity vector.
What is relative motion in the context of ‘Motion in a Plane’?
Relative motion refers to the perception of motion of one object from the viewpoint of another. It’s the motion of an object as observed from a particular frame of reference, which may also be in motion.
How does motion in a plane relate to real-world applications like sports or engineering?
Motion in a plane is crucial in various real-world applications, including sports like basketball, soccer, and golf, where players need to anticipate and calculate the trajectories of moving objects. In engineering, understanding motion in a plane is essential for designing structures, vehicles, and machinery that move in two dimensions, such as airplanes, cars, and robots.
