Newton’s Law of Cooling is like a recipe for predicting how fast a hot object will cool down. It’s named after Sir Isaac Newton, who formulated this law in the 17th century.
Before Newton, people noticed that hot objects cool down, but they didn’t have a good way to describe them mathematically. They could feel the warmth of a fire die down or watch a cup of tea cool, but the ‘how fast’ and ‘why’ were still mysteries.
Newton changed that. He proposed that the rate at which an object cools down is proportional to the temperature difference between the object and its surroundings. This was a big deal because it gave people a way to predict cooling rates.
Newton published his law of cooling in 1701. However, it’s important to note that the concepts of heat and temperature weren’t fully understood back then. Newton talked about the “degrees of heat” rather than temperature as we know it today.
Today, we interpret Newton’s Law of Cooling with a better understanding of thermodynamics. We use it to model the cooling of objects and even apply it in fields like forensic science to estimate the time of death.
What Is Newton’s Law of Cooling?
Picture a cup of steaming hot tea left to cool on a table or a warm baked pie cooling on a kitchen counter. These everyday scenes exemplify the essence of Newton’s Law of Cooling, a principle that governs how the temperature of an object changes when it is in contact with a surrounding medium at a different temperature.
Newton’s Law of Cooling provides valuable insights into the dynamics of heat transfer and temperature change, offering a fundamental understanding of how objects cool down or warm up when exposed to different environmental conditions.
Newton’s Law of Cooling describes how the temperature of an object changes over time as it loses or gains heat through radiation. It’s based on the observation that the rate at which an object cools down (or warms up) is proportional to the difference in temperature between the object and its surroundings.
Definition
Newton’s Law of Cooling states that the rate at which an object cools down is proportional to the difference in temperature between the object and its surroundings, as long as this temperature difference is not too large.
In simpler terms, if you have a hot cup of tea in a room, the tea will cool down quickly at first because it’s much hotter than the room. But as the tea gets closer to room temperature, it cools down more slowly. This happens because the bigger the difference in temperature between the tea and the room, the faster the heat will flow from the tea to the room. Once the temperatures are close, the flow of heat slows down.
Newton’s Law of Cooling Formula
The formula for Newton’s Law of Cooling helps us calculate how quickly an object will cool down to the temperature of its surroundings. It’s based on the idea that the rate of temperature change of an object is proportional to the difference in temperature between the object and its environment. The formula is expressed as:
\(\displaystyle\begin{equation}\label{eqn:1}\boxed{\boldsymbol{\frac{dT}{dt} = -k (T – T_s) }} \end{equation}\)
- \(\displaystyle\frac{dT}{dt} \) is the rate of change in temperature,
- (T) is the temperature of the object,
- (Ts) is the surrounding temperature,
- (k) is a constant that depends on the characteristics of the object.
The negative sign indicates that the temperature of the object decreases over time if it’s hotter than its surroundings. To put it simply, if you have a hot up of coffee in a room, the coffee will cool down faster when it’s much hotter than the room. As it gets closer to room temperature, it cools more slowly. The constant (k) tells us how fast this cooling happens, and it’s different for every object.
Derivation of Newton’s Law of Cooling
The law can be derived from the principle that the heat loss rate is proportional to the temperature difference. Integrating this rate over time gives us the formula mentioned above.
We have the equation \(\displaystyle\frac{dT}{dt} = -k (T – T_s) \), which tells us that the rate of change of temperature \(\displaystyle\frac{dT}{dt}\) is proportional to the difference between the object’s temperature (T) and the surrounding temperature (Ts), with (k) being the proportionality constant.
To solve this differential equation, we need to separate the variables (T) and (t). We can do this by dividing both sides by (T – Ts) and multiplying by (dt):
\(\displaystyle \frac{1}{T – T_s} dT = -k dt \)
Now we integrate both sides of the equation. The left side with respect to (T) and the right side with respect to (t):
\(\displaystyle \int \frac{1}{T – T_s} dT = \int -k dt \)
The integral of \(\displaystyle\frac{1}{T – T_s} \) with respect to (T) is the natural logarithm:
\(\displaystyle \ln |T – T_s| = -kt + C \)
Here, (C) is the constant of integration. Since temperature differences can be positive or negative, we remove the absolute value by introducing another constant (C’), which will absorb the sign:
\(\displaystyle \ln (T – T_s) = -kt + C’ \)
To get rid of the natural logarithm, we exponentiate both sides of the equation:
\(\displaystyle e^{\ln (T – T_s)} = e^{-kt + C’} \)
The exponential and the logarithm on the left side cancel each other out, and we use the property of exponents on the right side:
\(\displaystyle T – T_s = e^{C’} e^{-kt} \)
We introduce a new constant \(\displaystyle (C = e^{C’} )\), which is just the exponential of the integration constant:
\(\displaystyle T – T_s = Ce^{-kt} \)
Finally, we add (Ts) to both sides to solve for (T):
\(\displaystyle\begin{equation}\label{eqn:2}\boxed{\boldsymbol{ T = T_s + Ce^{-kt}}} \end{equation}\)
If we consider (T1) as the initial temperature at (t = 0) and (T2) as the temperature at some time ( t ), then ( C ) is (T1 – Ts), and we get:
\(\displaystyle\begin{equation}\label{eqn:3}\boxed{\boldsymbol{T_2 = T_s + (T_1 – T_s)e^{-kt}}} \end{equation}\)
This is the derived equation, which shows how the temperature (T2) at the time (t) relates to the initial temperature (T1), the surrounding temperature (Ts), and the cooling constant (k). It’s a fundamental result in thermodynamics that describes the cooling process according to Newton’s Law of Cooling.
Methods to Apply Newton’s Law of Cooling
When applying Newton’s Law of Cooling, we’re looking at how to use the formula to predict the temperature of an object over time as it cools down to the temperature of its surroundings. Here are some methods to do this:
- The formula \(\displaystyle\frac{dT}{dt} = -k (T – T_s) \) is a differential equation that can be solved to find the temperature (T) at any time (t).
- You’ll need to know the initial temperature of the object (T0), the surrounding temperature (Ts), and the cooling constant (k) which depends on the object’s properties.
- Sometimes, for simplicity, you can assume that the rate of cooling is constant, equal to the rate when the object’s temperature is at the average value during the cooling period.
- This method is an approximation and is useful when precise values are not required.
- You can plot the temperature of the object against time on a graph to visually analyze the cooling process.
- The slope of the line at any point gives the rate of cooling at that temperature.
- By measuring the temperature of an object over time as it cools, you can use the data to calculate the cooling constant (k) and verify Newton’s Law.
Verification of Newton’s Law of Cooling
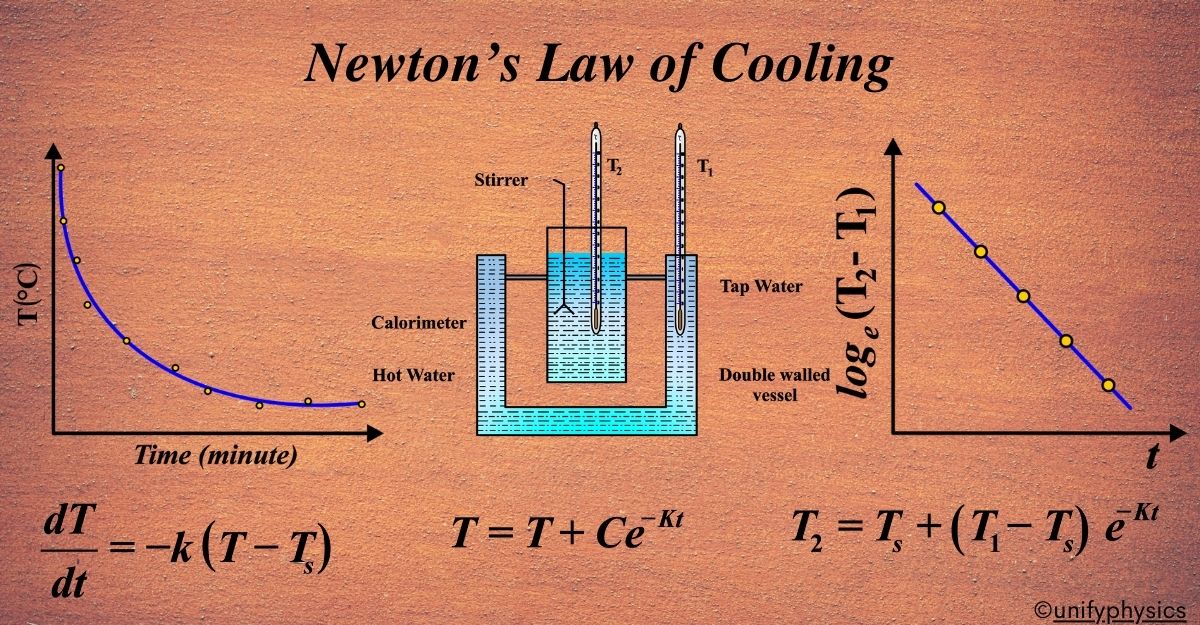
To verify Newton’s Law of Cooling, we can conduct a simple experiment: In the experiment, we used a special vessel with two walls, like a double-layered cup. Between these walls, we fill water. Inside this vessel, we place another cup made of copper, called a calorimeter, filled with hot water.
We have two thermometers. One thermometer, let’s call it T2, measures the temperature of the water inside the copper calorimeter. The other thermometer, T1, measures the temperature of the hot water between the two walls of the vessel.
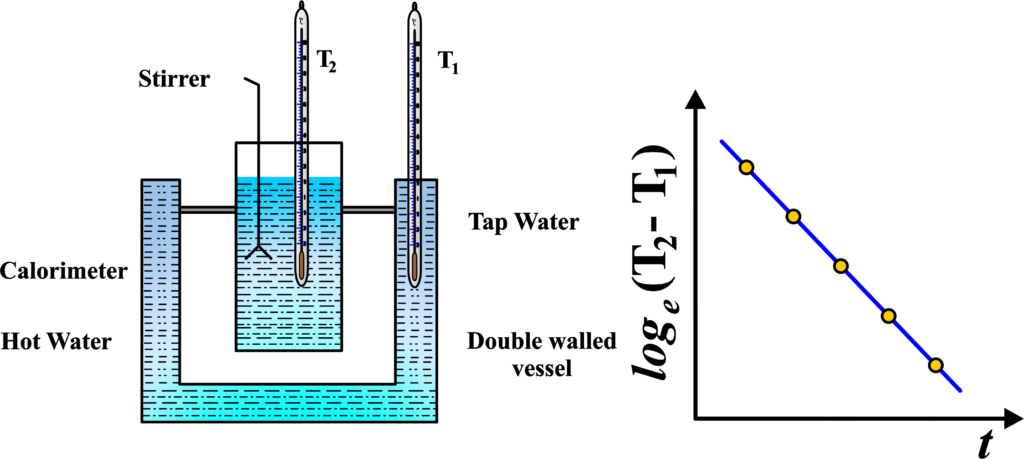
We note down the temperatures from both thermometers at regular intervals. Then, we plot a graph. On the graph, we put the difference between the temperatures from the two thermometers (T2 – T1) on the vertical axis and time (t) on the horizontal axis. When we plot this, we see a straight line with a negative slope.
This simple experiment helps us verify Newton’s Law of Cooling. It shows how the temperature of the hot water inside the vessel decreases over time, following a predictable pattern described by Newton’s Law of Cooling.
Newton’s Law of Cooling Graph
The graph for Newton’s Law of Cooling visually represents how the temperature of an object changes over time as it cools down to the temperature of its surroundings. Here’s what the graph typically looks like and what it means:
- The graph plots the temperature of the object on the y-axis against time on the x-axis.
- The shape of the curve is usually an exponential decay, meaning it starts steep and gradually flattens out as the object approaches the surrounding temperature.
- At the beginning, when the temperature difference between the object and the surroundings is greatest, the curve is steepest. This indicates rapid cooling.
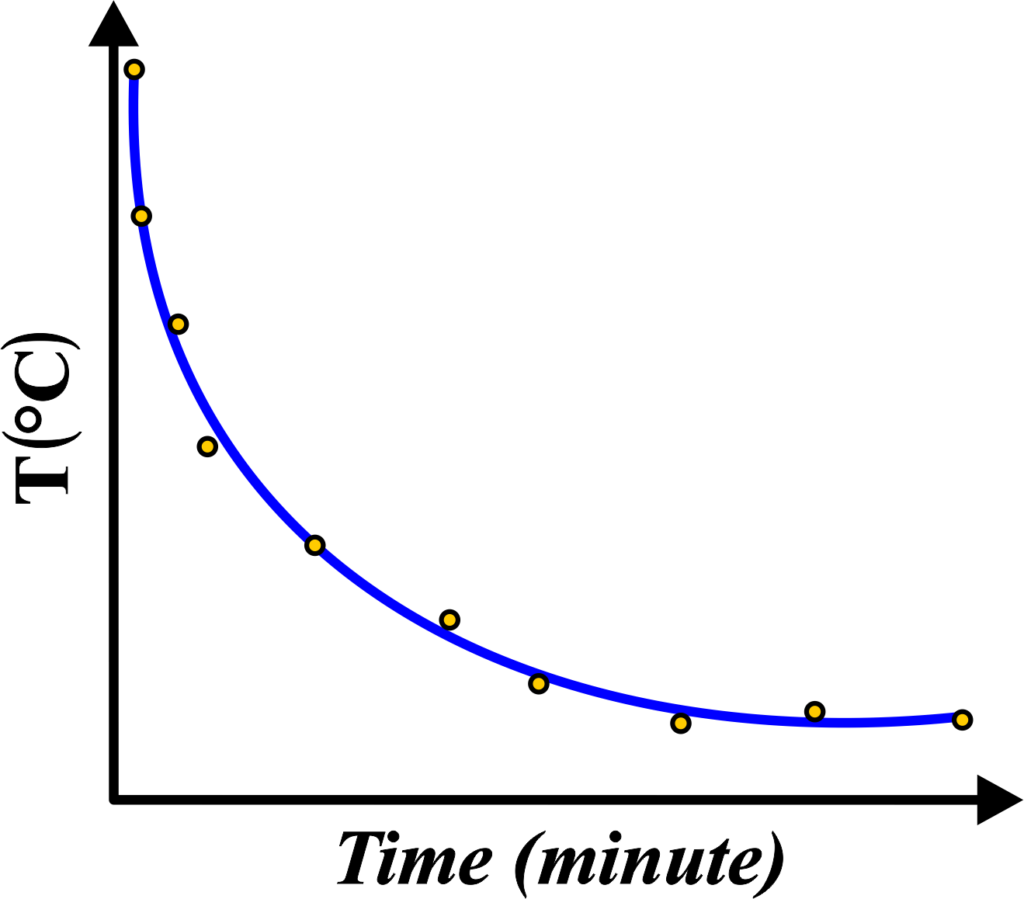
- As the object’s temperature gets closer to the surrounding temperature, the curve becomes less steep, showing that the rate of cooling is slowing down.
- Eventually, the curve levels off when the object’s temperature equals the surrounding temperature, indicating that thermal equilibrium has been reached.
- The slope at any point on the curve represents the rate of cooling at that moment. A steeper slope means a faster rate of cooling.
- If the graph is plotted on a semi-logarithmic scale, the slope of the straight line that the curve approximates can be used to determine the cooling constant (k).
This graph is a powerful tool for understanding how temperatures change over time according to Newton’s Law of Cooling. It helps students visualize the cooling process and the factors that affect it, such as the initial temperature difference and the properties of the object being cooled.
Limitations of Newton’s Law of Cooling
This law is limited to situations where the temperature difference is small and does not account for all forms of heat transfer, such as conduction and convection.
- The law assumes that the temperature difference between the object and its surroundings is small. If the difference is too large, the law does not accurately describe the cooling process.
- It presumes that the heat loss from the object is solely due to radiation. In reality, heat can also be lost through conduction and convection, which the law does not account for.
- The surrounding temperature is assumed to be constant. If the surrounding temperature changes, the law’s predictions may not be accurate.
- The law implies a linear relationship between the rate of cooling and the temperature difference. However, in many real-world situations, this relationship can be more complex.
- Newton’s Law of Cooling does not consider internal heat sources within the object, which could affect the cooling rate.
- While the law is primarily applicable to situations where radiation is the main form of heat transfer, it is less applicable to processes dominated by conduction and convection.
Applications of Newton’s Law of Cooling
The law is used in various applications, including forensic science to estimate the time of death, environmental science to model cooling rates of land and water, and engineering to design cooling systems.
- The law can be used to predict how long it will take for an object, like a cup of tea or a baked pie, to cool down to room temperature.
- Forensic investigations, help estimate the time of death by comparing the current body temperature with what it likely was at the time of death.
- It’s used to calculate how long it will take for food or drinks to reach a certain temperature when placed in a refrigerator.
- Engineers use this law to design cooling systems for electronic devices and machinery to ensure they operate safely within their temperature limits.
- It helps in studying the cooling rates of land and water bodies, which is important for understanding local climates and weather patterns.
- The law aids in designing medical treatments that involve heating or cooling parts of the body, ensuring patient safety and treatment efficacy.
- In industries, it’s applied to control the temperature of processes such as chemical reactions, which must be kept within specific temperature ranges for safety and quality.
Also Read: Calorimetry
Solved Examples
Problem 1: A cup of coffee at 90°C is left in a room with a constant temperature of 20°C. If the cooling constant is (\(\displaystyle k = 0.1 \, \text{min}^{-1} \)), find the temperature of the coffee after 10 minutes.
Solution: Using Newton’s Law of Cooling:
\(\displaystyle T(t) = T_{\text{room}} + (T_{\text{initial}} – T_{\text{room}}) e^{-kt} \)
Where:
- (\(\displaystyle T_{\text{room}} = 20^\circ\text{C} \))
- (\(\displaystyle T_{\text{initial}} = 90^\circ\text{C} \))
- (\(\displaystyle k = 0.1 \, \text{min}^{-1} \)
- (t = 10 min)
Calculation:
\(\displaystyle T(10) = 20 + (90 – 20) e^{-0.1 \times 10} \)
\(\displaystyle T(10) = 20 + 70 e^{-1} \)
\(\displaystyle T(10) = 20 + 70 \times 0.3679 \)
\(\displaystyle T(10) = 20 + 25.753 \)
\(\displaystyle T(10) \approx 45.75^\circ\text{C} \)
The temperature of the coffee after 10 minutes is approximately (45.75∘C).
Problem 2: A hot object at 80°C cools to 60°C in 5 minutes in a room at 20°C. Assuming the cooling constant remains the same, how long will it take for the object to cool to 30°C?
Solution: Using Newton’s Law of Cooling:
\(\displaystyle T(t) = T_{\text{room}} + (T_{\text{initial}} – T_{\text{room}}) e^{-kt} \)
First, find the cooling constant (k) using the first set of temperatures:
\(\displaystyle 60 = 20 + (80 – 20) e^{-5k} \)
\(\displaystyle 60 = 20 + 60 e^{-5k} \)
\(\displaystyle 40 = 60 e^{-5k} \)
\(\displaystyle \frac{2}{3} = e^{-5k} \)
\(\displaystyle \ln\left(\frac{2}{3}\right) = -5k \)
\(\displaystyle k = -\frac{\ln\left(\frac{2}{3}\right)}{5} \)
\(\displaystyle k \approx 0.0811 \, \text{min}^{-1} \)
Now, use this (k) to find the time for cooling to 30°C:
\(\displaystyle 30 = 20 + (80 – 20) e^{-0.0811t} \)
\(\displaystyle 30 = 20 + 60 e^{-0.0811t} \)
\(\displaystyle 10 = 60 e^{-0.0811t} \)
\(\displaystyle \frac{1}{6} = e^{-0.0811t} \)
\(\displaystyle \ln\left(\frac{1}{6}\right) = -0.0811t \)
\(\displaystyle t = -\frac{\ln\left(\frac{1}{6}\right)}{0.0811} \)
\(\displaystyle t \approx 24.57 \, \text{min} \)
It will take approximately 24.57 minutes for the object to cool to 30°C.
Problem 3: An object cools from 100°C to 80°C in 4 minutes in a room at 25°C. Find the cooling constant (k).
Solution: Using Newton’s Law of Cooling:
\(\displaystyle T(t) = T_{\text{room}} + (T_{\text{initial}} – T_{\text{room}}) e^{-kt} \)
Given:
- (\(\displaystyle T_{\text{initial}} = 100^\circ\text{C} \))
- (\(\displaystyle T(t) = 80^\circ\text{C} \))
- (\(\displaystyle T_{\text{room}} = 25^\circ\text{C} \))
- (t = 4 min)
Calculation:
\(\displaystyle 80 = 25 + (100 – 25) e^{-4k} \)
\(\displaystyle 80 = 25 + 75 e^{-4k} \)
\(\displaystyle 55 = 75 e^{-4k} \)
\(\displaystyle \frac{55}{75} = e^{-4k} \)
\(\displaystyle \frac{11}{15} = e^{-4k} \)
\(\displaystyle \ln\left(\frac{11}{15}\right) = -4k \)
\(\displaystyle k = -\frac{\ln\left(\frac{11}{15}\right)}{4} \)
\(\displaystyle k \approx 0.0942 \, \text{min}^{-1} \)
The cooling constant (k) is approximately (\(\displaystyle 0.0942 \, \text{min}^{-1} \)).
Problem 4: A metal rod initially at 150°C is placed in a room at 30°C. If the temperature of the rod drops to 100°C in 8 minutes, how long will it take for the rod to reach 50°C?
Solution: First, find the cooling constant (k):
\(\displaystyle 100 = 30 + (150 – 30) e^{-8k} \)
\(\displaystyle 100 = 30 + 120 e^{-8k} \)
\(\displaystyle 70 = 120 e^{-8k} \)
\(\displaystyle \frac{7}{12} = e^{-8k} \)
\(\displaystyle \ln\left(\frac{7}{12}\right) = -8k \)
\(\displaystyle k = -\frac{\ln\left(\frac{7}{12}\right)}{8} \)
\(\displaystyle k \approx 0.0520 \, \text{min}^{-1} \)
Now, find the time to cool to 50°C:
\(\displaystyle 50 = 30 + (150 – 30) e^{-0.0520t}\)
\(\displaystyle 50 = 30 + 120 e^{-0.0520t}\)
\(\displaystyle 20 = 120 e^{-0.0520t} \)
\(\displaystyle \frac{1}{6} = e^{-0.0520t} \)
\(\displaystyle \ln\left(\frac{1}{6}\right) = -0.0520t \)
\(\displaystyle t = -\frac{\ln\left(\frac{1}{6}\right)}{0.0520} \)
\(\displaystyle t \approx 35.58 \, \text{min}\)
It will take approximately 35.58 minutes for the rod to cool to 50°C.
Problem 5: Two identical cups of tea are left to cool in different rooms. In-room A (25°C), the tea cools from 90°C to 60°C in 10 minutes. In room B (20°C), how long will it take for the tea to cool from 90°C to 60°C?
Solution: Find the cooling constant (k) in room A:
\(\displaystyle 60 = 25 + (90 – 25) e^{-10k} \)
\(\displaystyle 60 = 25 + 65 e^{-10k} \)
\(\displaystyle 35 = 65 e^{-10k} \)
\(\displaystyle \frac{7}{13} = e^{-10k} \)
\(\displaystyle \ln\left(\frac{7}{13}\right) = -10k \)
\(\displaystyle k = -\frac{\ln\left(\frac{7}{13}\right)}{10} \)
\(\displaystyle k \approx 0.0603 \, \text{min}^{-1} \)
Now, find the time in room B:
\(\displaystyle 60 = 20 + (90 – 20) e^{-0.0603t} \)
\(\displaystyle 60 = 20 + 70 e^{-0.0603t} \)
\(\displaystyle 40 = 70 e^{-0.0603t} \)
\(\displaystyle \frac{4}{7} = e^{-0.0603t} \)
\(\displaystyle \ln\left(\frac{4}{7}\right) = -0.0603t \)
\(\displaystyle t = -\frac{\ln\left(\frac{4}{7}\right)}{0.0603} \)
\(\displaystyle t \approx 15.02 \, \text{min} \)
It will take approximately 15.02 minutes for the tea to cool from 90°C to 60°C in room B.
Problem 6: Two different liquids, A and B, are left to cool in the same room (25°C). Liquid A cools from 80°C to 60°C in 5 minutes, and liquid B cools from 80°C to 60°C in 7 minutes. Compare the cooling constants of the two liquids.
Solution: Find the cooling constant (k) for liquid A:
\(\displaystyle 60 = 25 + (80 – 25) e^{-5k_A} \)
\(\displaystyle 60 = 25 + 55 e^{-5k_A} \)
\(\displaystyle 35 = 55 e^{-5k_A} \)
\(\displaystyle \frac{35}{55} = e^{-5k_A} \)
\(\displaystyle \frac{7}{11} = e^{-5k_A} \)
\(\displaystyle \ln\left(\frac{7}{11}\right) = -5k_A \)
\(\displaystyle k_A = -\frac{\ln\left(\frac{7}{11}\right)}{5} \)
\(\displaystyle k_A \approx 0.0736 \, \text{min}^{-1}\)
Find the cooling constant (k) for liquid B:
\(\displaystyle 60 = 25 + (80 – 25) e^{-7k_B} \)
\(\displaystyle 60 = 25 + 55 e^{-7k_B} \)
\(\displaystyle 35 = 55 e^{-7k_B} \)
\(\displaystyle \frac{35}{55} = e^{-7k_B} \)
\(\displaystyle \frac{7}{11} = e^{-7k_B} \)
\(\displaystyle \ln\left(\frac{7}{11}\right) = -7k_B \)
\(\displaystyle k_B = -\frac{\ln\left(\frac{7}{11}\right)}{7} \)
\(\displaystyle k_B \approx 0.0526 \, \text{min}^{-1}\)
The cooling constant (kA) for liquid A is approximately (\(\displaystyle 0.0736 \, \text{min}^{-1} \)), and the cooling constant (kB) for liquid B is approximately (\(\displaystyle 0.0526 \, \text{min}^{-1} \)). Liquid A cools faster than liquid B.
FAQs
What exactly is Newton’s Law of Cooling?
Newton’s Law of Cooling describes how the temperature of an object changes over time as it either cools down or warms up to match the temperature of its surroundings.
How does Newton’s Law of Cooling apply to everyday life?
This law can be seen in action when you let a hot cup of coffee cool to room temperature, or when you heat a cold bowl of soup until it’s warm.
Does Newton’s Law of Cooling only apply to cooling objects?
No, it applies to both cooling and warming. It’s about reaching thermal equilibrium with the environment, whether that means losing or gaining heat.
Can Newton’s Law of Cooling tell us how long it will take for something to cool?
Yes, it provides a way to estimate the time it will take for an object to cool down to a certain temperature, although it requires some additional information to make that calculation.
Is Newton’s Law of Cooling used in any professions?
It’s used in fields like forensic science to estimate the time of death, in culinary arts to ensure food safety, and in engineering to design cooling systems.
Why is it important for us to understand Newton’s Law of Cooling?
Understanding this law helps us predict and manage temperature changes in various situations, from industrial processes to everyday tasks like cooking.
Does the size of an object affect how Newton’s Law of Cooling applies to it?
Yes, the size and shape of an object can influence how quickly it cools or warms because they affect the object’s surface area and how it interacts with its environment.