Nuclear Fission

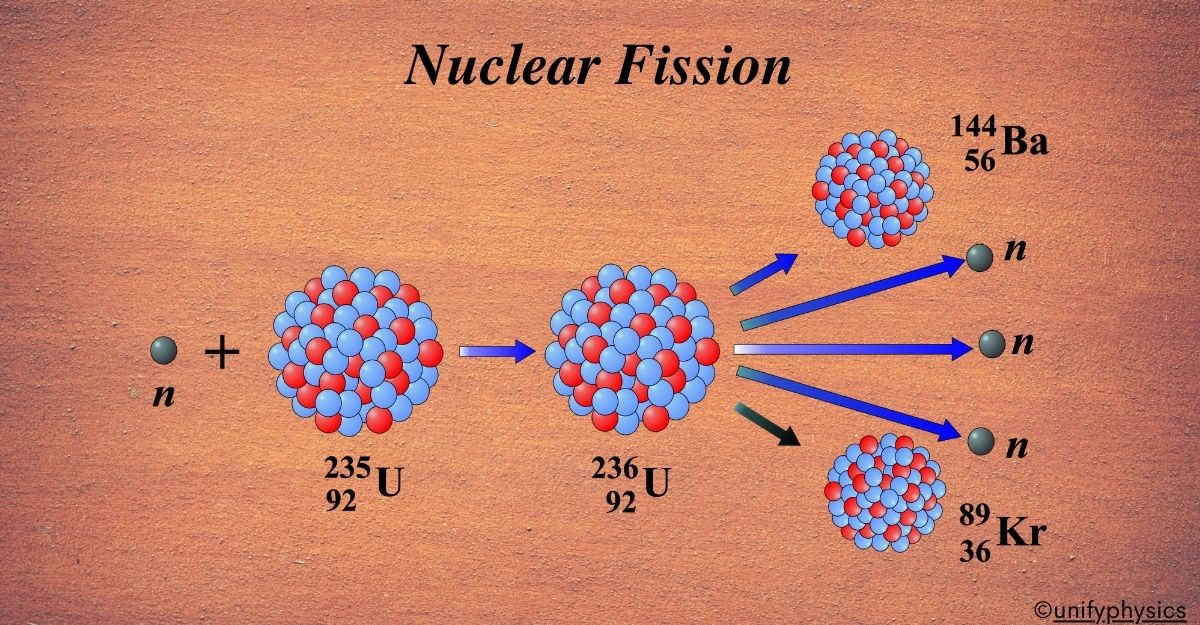
The discovery of nuclear fission marked a significant milestone in atomic physics. It all began on December 19, 1938, in Berlin, when German chemists Otto Hahn and Fritz Strassmann were conducting experiments bombarding uranium with neutrons. To their surprise, they found that instead of creating a heavier element as expected, the uranium nucleus split into smaller elements, one of which was barium.

This unexpected result puzzled the scientific community. It was Lise Meitner and her nephew Otto Robert Frisch, both physicists, who provided the theoretical explanation for this phenomenon in January 1939 while they were in Stockholm. They realized that the uranium nucleus, when absorbing a neutron, became so unstable that it split into two lighter nuclei, releasing a significant amount of energy in the process.

Frisch coined the term “fission” by analogy with the biological fission of living cells, as it resembled the process where one entity splits into two. This discovery not only advanced our understanding of atomic structure but also paved the way for the development of nuclear reactors and atomic bombs, due to the vast amounts of energy released during fission.

What Is Nuclear Fission?

It’s a process where the nucleus of an atom splits into two or more smaller nuclei, along with a few neutrons and a large amount of energy. Imagine you have a large, heavy ball, and suddenly it splits into two smaller balls. This is similar to what happens in nuclear fission, but with atomic nuclei.

Nuclear fission is a process where the nucleus of a heavy atom, like uranium or plutonium, absorbs a neutron and becomes so unstable that it cannot hold itself together. As a result, it splits into two smaller nuclei, which are called fission products. This splitting also releases additional neutrons and a tremendous amount of energy.

The energy released during fission comes from the strong nuclear force, one of the four fundamental forces in physics. This force holds the protons and neutrons together in the nucleus. When the nucleus splits, the strong nuclear force releases energy as the fission products move away from each other at high speeds.

Fission is a form of nuclear transmutation because the resulting fragments are different elements from the original atom. The two new nuclei produced are usually not identical but have comparable sizes, often with a mass ratio of about 3 to 2.

Nuclear Fusion vs. Nuclear Fission

Both nuclear fusion and fission are reactions that produce energy, but they work in opposite ways.

Nuclear Fission is like breaking a large rock into two smaller stones. It involves the splitting of a heavy, unstable nucleus (like uranium) into two lighter nuclei. This process releases energy and additional neutrons. It’s the reaction used in nuclear power plants and atomic bombs.

Nuclear Fusion, on the other hand, is like molding two small clay balls into one big ball. It occurs when two light atomic nuclei (like hydrogen isotopes) merge to form a heavier nucleus (like helium). This process releases even more energy than fission and is what powers the sun and other stars. Fusion produces less radioactive waste compared to fission and is seen as a potential source of almost limitless and cleaner energy.

Fission: Splitting of heavy nuclei into lighter nuclei.
Fusion: Combining light nuclei into a heavier nucleus.

Fusion releases more energy than fission and has a lower risk of radioactive contamination, but it’s also harder to achieve and control on Earth. Scientists are working on making fusion a practical energy source, but as of now, fission is the main nuclear reaction used for energy production.

Aspect	Nuclear Fusion	Nuclear Fission
Basic Process	Combining two light atoms to form a heavier atom.	Splitting a heavy atom into two or more lighter atoms.
Energy Released	Releases more energy compared to fission.	Releases less energy compared to fusion.
Conditions Required	Requires extremely high temperatures and pressures (like those found in stars).	Can occur at lower temperatures and pressures, making it easier to achieve on Earth.
Radioactive Waste	Produces minimal radioactive byproducts.	Generates significant amounts of radioactive waste.
Fuel Source	Uses isotopes of hydrogen, like deuterium and tritium.	Uses heavy elements like uranium or plutonium.
Safety	Inherently safer due to less radioactive waste and no risk of meltdown.	Risk of accidents and meltdowns with long-term environmental impact.
Current Usage	Still in the experimental stages; and not yet used for commercial energy production.	Widely used for commercial energy production in nuclear reactors.

This process is fundamental to how nuclear reactors work, providing the energy needed to generate electricity. It’s also the reaction that powers atomic bombs, releasing energy rapidly and explosively.

Examples of Nuclear Fission

The fission of uranium-235 and plutonium-239 are common examples used in nuclear reactors and atomic bombs.

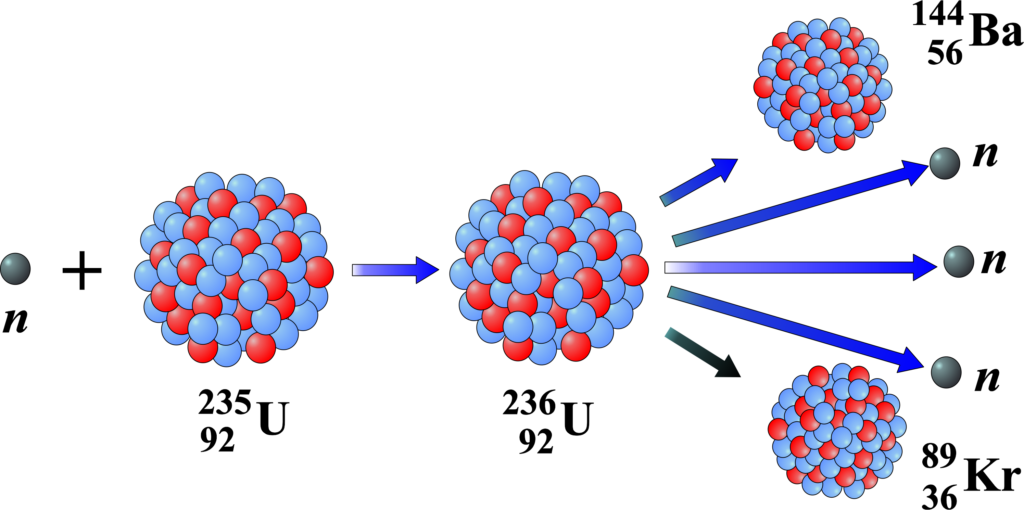
Uranium-235 Fission: This is a classic example where a uranium-235 nucleus absorbs a neutron and splits into two smaller nuclei, along with additional neutrons and energy. The equation for this reaction is:

\(\displaystyle ^{235}U + ^1n \rightarrow ^{141}Ba + ^{92}Kr + 3 ^1n\)

Here, uranium-235 (²³⁵U) is bombarded with a neutron (¹n), resulting in the formation of barium-141 (¹⁴¹Ba), krypton-92 (⁹²Kr), and three more neutrons (³1n).

Uranium-235 Fission Reaction Process The fission reaction of Uranium-235 (U-235) is a multi-step process that can be described as follows:

A U-235 nucleus captures a slow-moving (thermal) neutron, becoming an excited U-236 nucleus. The U-236 nucleus is highly unstable and quickly splits into two smaller nuclei, known as fission fragments. These fragments are usually not the same size but are comparable in mass.

Along with the fission fragments, two or three free neutrons are ejected. The exact number can vary, but on average, about 2.43 neutrons are released per fission event by thermal neutrons. If these free neutrons strike other U-235 nuclei, they can cause those nuclei to undergo fission as well, potentially leading to a chain reaction if conditions allow.

The fission fragments are typically isotopes of different elements such as krypton and barium, and they are usually radioactive. The reaction also releases gamma rays, which are a form of electromagnetic radiation.

Here’s a simplified representation of what a U-235 fission reaction might look like:

\(\displaystyle\text{U-235} + \text{n} \rightarrow \text{U-236} \rightarrow \text{Fission Fragments} + 2\text{ or }3\text{ n} + \gamma \)

This equation shows that when a uranium-235 nucleus absorbs a neutron (n), it becomes an excited uranium-236 nucleus, which then splits into fission fragments, additional neutrons, and gamma rays (γ).

Plutonium-239 vs. Uranium-235

Plutonium-239 and Uranium-235 are both used as fuel in nuclear reactors and as material in nuclear weapons due to their ability to sustain a nuclear chain reaction. However, there are some key differences:

Uranium-235 is a naturally occurring isotope found in uranium ore, albeit it’s rare, making up about 0.7% of natural uranium. Plutonium-239, on the other hand, does not occur naturally and is produced artificially in nuclear reactors from uranium-238.

Plutonium-239 is created in a reactor when uranium-238 absorbs a neutron and undergoes a series of beta decays. Uranium-235 can be separated from natural uranium by a process called enrichment. Plutonium-239 has a lower critical mass than uranium-235, which means less material is needed to sustain a chain reaction. This makes plutonium-239 more suitable for use in nuclear weapons.

Both isotopes can undergo fission when struck by a neutron, but the fission of plutonium-239 releases more neutrons on average compared to uranium-235. This property is crucial for the efficiency of nuclear reactors and the explosiveness of nuclear weapons.

Both plutonium-239 and uranium-235 are fissile materials capable of sustaining a chain reaction, they differ in their natural occurrence, production methods, critical mass requirements, and specific fission properties.

Plutonium-239 Fission:

Similar to uranium-235, plutonium-239 can also undergo fission when it captures a neutron. The fission of plutonium-239 can produce various combinations of fission products, including isotopes of xenon and strontium. Plutonium-239 (Pu-239) fission is a nuclear reaction where the nucleus of a plutonium-239 atom splits into two smaller nuclei after absorbing a neutron. Here’s how it happens:

A Pu-239 nucleus captures a neutron, which may be slow-moving (thermal) or fast. This makes the Pu-239 nucleus highly unstable. The unstable Pu-239 nucleus splits into two smaller nuclei, known as fission fragments. These fragments are typically different in size and are isotopes of other elements.

The fission process releases additional neutrons (on average about 2.89 neutrons per fission by thermal neutron). These neutrons can then initiate further fission reactions if they collide with other Pu-239 nuclei. If there is a sufficient amount of Pu-239 and the conditions are right, these neutrons can sustain a chain reaction, where each fission event causes additional fission events.

The fission fragments are usually radioactive and will eventually decay into stable isotopes over time. Gamma rays are also emitted during the fission process, which is a type of electromagnetic radiation.

Here’s a simplified representation of what a Pu-239 fission reaction might look like:

\(\displaystyle\text{Pu-239} + \text{n} \rightarrow \text{Pu-240} \rightarrow \text{Fission Fragments} + 2\text{ or }3\text{ n} + \gamma\)

This equation shows that when a plutonium-239 nucleus absorbs a neutron (n), it becomes an excited plutonium-240 nucleus, which then splits into fission fragments, additional neutrons, and gamma rays (γ). These reactions are fundamental to how nuclear power plants generate electricity. The additional neutrons released can go on to cause more fission reactions in other nuclei, creating a chain reaction that releases a significant amount of energy.

The Energy of Nuclear Fission

The energy released during fission comes from the strong nuclear forces holding the nucleus together. When split, this energy is released as kinetic energy of the fission products and as electromagnetic radiation.

In nuclear fission, a large amount of energy is released when the nucleus of an atom splits into two smaller nuclei. This energy comes from the strong nuclear forces that hold the protons and neutrons together in the nucleus. When the nucleus splits, these forces are overcome, and the energy that was holding the nucleus together is released.

• Kinetic Energy: The majority of the energy (about 85%) is released in the form of kinetic energy of the fission fragments. These fragments move away from each other at high speeds due to the repulsive forces between them.
• Neutron Energy: The neutrons that are ejected during fission carry about 6% of the total energy.
• Gamma Rays: Gamma rays, which are a form of electromagnetic radiation, carry another 6% of the total energy.
• Beta Decay: Some of the fission products are radioactive and will undergo beta decay, releasing additional gamma rays and antineutrinos.
• Antineutrinos: About 3% of the energy is carried away by antineutrinos, which are nearly massless particles that rarely interact with matter.

To give you an idea of the amount of energy involved, the fissioning of 1 gram of Uranium-235 (U-235) can yield about one megawatt-day (MWd) of heat energy. This is because each U-235 fission releases about 210 million electron volts (MeV) of energy.

The mass-energy equivalence principle, famously represented by Einstein’s equation (\(\displaystyle E = mc^2 \)), explains that a small amount of mass is converted into a large amount of energy during fission. This conversion is what makes nuclear fission a powerful source of energy.

Basics of Nuclear Fission

Nuclear fission is a process where the nucleus of an atom, typically a heavy element like uranium or plutonium, splits into two smaller nuclei. This fundamental concept is crucial in understanding how nuclear reactions occur and how they can be harnessed for energy.

Fission usually involves heavy nuclei, which are unstable due to the large number of protons and neutrons they contain. When fission occurs, the heavy nucleus splits into two smaller nuclei, which are called fission fragments. These fragments are usually not equal in size but have roughly half the protons and neutrons of the original nucleus.

Along with the fission fragments, a few free neutrons are also released. These neutrons can go on to cause more fission reactions in other nuclei, potentially leading to a chain reaction.

The splitting of the nucleus releases a significant amount of energy. This energy comes from the conversion of mass into energy, as described by Einstein’s famous equation (\(\displaystyle E = mc^2 \)).

If enough fissionable material is present and the conditions are right, a self-sustaining chain reaction can occur, where each fission event causes further fission events. The minimum amount of fissile material needed to maintain a chain reaction is called the critical mass.

In nuclear reactors, the chain reaction is controlled to produce energy steadily over time. In nuclear weapons, the reaction is uncontrolled, leading to an explosive release of energy.

Here’s a simple representation of a nuclear fission reaction:

\(\displaystyle\text{Heavy Nucleus} \rightarrow \text{Fission Fragments} + \text{Neutrons} + \text{Energy}\)

The Mechanism of Nuclear Fission Reaction

When a nucleus fissions, it splits into two smaller nuclei (fission fragments), releases two or three neutrons, and emits gamma rays. The released neutrons can then cause more fissions. The mechanism of nuclear fission involves several steps that lead to the splitting of a heavy atomic nucleus into smaller nuclei.

The process often begins when a neutron is absorbed by a heavy nucleus, such as uranium-235 (U-235). This absorption makes the nucleus unstable. The absorption of the neutron adds energy to the nucleus, causing it to become excited and vibrate.

Due to these vibrations, the nucleus becomes deformed, elongating, and taking on an ellipsoidal shape. As the deformation increases, the nuclear forces can no longer hold the nucleus together, and it splits into two smaller nuclei, known as fission fragments.

Along with the fission fragments, additional neutrons are released. These neutrons can then be absorbed by other fissile nuclei, continuing the reaction. The mass of the fission fragments and released neutrons is less than the original mass of the heavy nucleus and absorbed neutron. This “missing” mass is converted into energy, released as kinetic energy of the fragments and as gamma radiation.

If each neutron released causes another fission event, a chain reaction can occur. This chain reaction is what powers nuclear reactors and makes nuclear bombs possible.

• Neutron absorption: (\(\displaystyle \text{U-235} + \text{n} \rightarrow \text{U-236}^* \))
• Nucleus excitation and deformation
• Nuclear splitting: (\(\displaystyle \text{U-236}^* \rightarrow \text{Fission Fragments} + 2\text{n} + \text{Energy} \))

Nuclear Fission Reactor

A controlled environment where nuclear fission reactions occur to produce heat, which is then used to generate electricity. Here’s a detailed explanation of each part of a nuclear fission reactor and their functions:

• The Core: The heart of the reactor, the core contains the nuclear fuel (usually uranium-235 or plutonium-239) that undergoes fission. The core generates the heat required for energy production.
• Neutron Moderator: This component, often made of water or graphite, slows down the fast neutrons produced during fission. Slow neutrons are more effective in sustaining the chain reaction.
• Control Rods: Made from materials like boron or cadmium that absorb neutrons, control rods regulate the rate of the fission reaction. Inserting them into the core slows down the reaction while removing them speeds it up.
• Coolant: A fluid (which can be water, gas, or liquid metal) that flows through the core to remove the heat generated by fission. The coolant prevents the reactor from overheating.
• Heat Exchanger: This system transfers the heat from the coolant to another loop of water, which turns into steam without becoming radioactive.
• Turbine and Generator: The steam produced in the heat exchanger drives a turbine connected to a generator. As the turbine spins, it converts kinetic energy into electrical energy.
• Containment Structure: A robust and sealed structure that houses all the other components. It’s designed to contain any radiation or radioactive materials in case of an accident.

Also Read: Radioactivity

Advantages/Disadvantages of Nuclear Fission

Advantages:

• Low Emissions: Nuclear fission produces a minimal amount of greenhouse gases compared to fossil fuels, making it a cleaner energy source that helps combat climate change.
• High Energy Density: A small amount of nuclear fuel can produce a large amount of energy; for example, 1 kg of uranium can release as much energy as burning several thousand kilograms of coal.
• Reliability: Nuclear power plants can operate continuously for long periods before needing refueling, providing a stable and reliable energy source.
• Low Operational Costs: Once a nuclear power plant is built, the operational costs are relatively low compared to other forms of energy production.
• Safety Record: Despite high-profile accidents, statistically, nuclear power has caused fewer fatalities per unit of energy produced than other major forms of power generation.
• Energy Independence: Countries can reduce their dependence on imported fossil fuels by using nuclear fission to generate electricity.
• Small Land Footprint: Nuclear power plants require less land than renewable energy sources like solar or wind farms, making them suitable for areas with limited space.

These advantages show why nuclear fission is considered a significant source of energy for the future, especially when looking for ways to reduce carbon emissions and ensure energy security.

Disadvantages:

• Radioactive Waste: Nuclear fission produces radioactive waste that remains hazardous for thousands of years and requires secure, long-term storage solutions.
• High Initial Costs: Building a nuclear power plant requires a significant investment due to the complexity and safety measures needed.
• Nuclear Accidents: Although rare, accidents at nuclear power plants can have severe and long-lasting environmental and health impacts.
• Non-Renewable: The uranium or plutonium used as fuel in nuclear reactors is finite and not renewable, similar to fossil fuels.
• Thermal Pollution: The warm water discharged from nuclear power plants can affect local aquatic ecosystems.
• Security Risks: Nuclear materials can be a target for theft to create weapons, posing a security risk.
• Decommissioning Costs: After a nuclear power plant’s life ends, it must be decommissioned, which is a complex and costly process.

Solved Examples

Problem 1:Calculate the energy released in the fission of Uranium-235 when it splits into Barium-141 and Krypton-92 along with 3 neutrons. Given the atomic masses are:

• (\(\displaystyle^{235}_{92}\text{U} = 235.0439299 \, \text{u}\))
• (\(\displaystyle^{141}_{56}\text{Ba} = 140.914411 \, \text{u}\))
• (\(\displaystyle^{92}_{36}\text{Kr} = 91.926156 \, \text{u}\))
• neutron = 1.008664 u

Solution: The fission reaction can be represented as,

\(\displaystyle ^{235}_{92}\text{U} + n \rightarrow ^{141}_{56}\text{Ba} + ^{92}_{36}\text{Kr} + 3n \)

The total mass before fission:

\(\displaystyle m_{\text{before}} = 235.0439299 \, \text{u} + 1.008664 \, \text{u} = 236.0525939 \, \text{u} \)

The total mass after fission:

\(\displaystyle m_{\text{after}} = 140.914411 \, \text{u} + 91.926156 \, \text{u} + 3 \times 1.008664 \, \text{u} = 235.866559 \, \text{u} \)

The mass defect (∆m):

\(\displaystyle \Delta m = m_{\text{before}} – m_{\text{after}} = 236.0525939 \, \text{u} – 235.866559 \, \text{u} = 0.1860349 \, \text{u} \)

Convert mass defect to energy (1 u = 931.5 MeV):

\(\displaystyle E = \Delta m \times 931.5 \, \text{MeV/u} = 0.1860349 \times 931.5 \, \text{MeV} = 173.17 \, \text{MeV}\)

The energy released in the fission of one Uranium-235 nucleus is approximately 173.17 MeV.

Problem 2: Describe the mechanism of a nuclear chain reaction starting with one fission of Uranium-235 and the production of three neutrons. Assume each neutron causes one subsequent fission.

Solution:

A nuclear chain reaction occurs when the neutrons produced from a single fission event cause additional fission reactions, releasing more neutrons, and thus sustaining the reaction.

A Uranium-235 nucleus absorbs a neutron and undergoes fission. This fission event produces 2-3 neutrons, typically three. Each of these neutrons can be absorbed by other Uranium-235 nuclei, causing further fission. Each of these subsequent fission events produces more neutrons, perpetuating the chain reaction.

Mathematically:

• 1 fission event → 3 neutrons → 3 fission events.
• 3 fission events → 9 neutrons → 9 fission events. And so on.

The reaction grows exponentially, releasing a tremendous amount of energy in a very short time if uncontrolled. The mechanism of a nuclear chain reaction involves each fission event releasing neutrons that induce further fission events, leading to an exponential increase in reactions and energy release.

Problem 3: Explain why a certain minimum mass of Uranium-235, known as the critical mass, is necessary to sustain a chain reaction.

Solution:

Critical mass is the minimum amount of fissile material needed to maintain a self-sustaining nuclear chain reaction. It depends on several factors:

1. Surface Area to Volume Ratio: As the size of the fissile material increases, the volume increases faster than the surface area, reducing the probability of neutrons escaping the material without causing further fission.

2. Neutron Reflection: Surrounding the fissile material with a reflector reduces neutron loss by bouncing escaping neutrons back into the material.

3. Purity and Density: Higher purity and density of the fissile material increase the likelihood of neutrons causing further fission.

If the mass is below the critical level, neutrons escape too quickly to sustain the chain reaction.

A critical mass of Uranium-235 is necessary to ensure that enough neutrons are captured within the material to sustain a chain reaction, influenced by geometry, neutron reflection, and material purity/density.

Problem 4: Calculate the energy output per day of a nuclear reactor using 1 kg of Uranium-235, assuming 200 MeV of energy is released per fission and the reactor operates at 90% efficiency.

Solution: Calculate the number of Uranium-235 atoms in 1 kg:

\(\displaystyle \text{Number of atoms} = \frac{\text{mass}}{\text{molar mass}} \times N_A \)

\(\displaystyle = \frac{1000 \, \text{g}}{235 \, \text{g/mol}} \times 6.022 \times 10^{23} \, \text{atoms/mol} \)

\(\displaystyle = 2.56 \times 10^{24} \, \text{atoms} \)

The energy released per fission:

\(\displaystyle E_{\text{fission}} = 200 \, \text{MeV} = 200 \times 1.60218 \times 10^{-13} \, \text{J} \)

\(\displaystyle = 3.20436 \times 10^{-11} \, \text{J} \)

Total energy released by 1 kg of Uranium-235:

\(\displaystyle E_{\text{total}} = 2.56 \times 10^{24} \, \text{atoms} \times 3.20436 \times 10^{-11} \, \text{J/atom} \)

\(\displaystyle = 8.20 \times 10^{13} \, \text{J} \)

Considering the reactor efficiency:

\(\displaystyle E_{\text{output}} = E_{\text{total}} \times 0.90 \)

\(\displaystyle = 8.20 \times 10^{13} \times 0.90 \)

\(\displaystyle = 7.38 \times 10^{13} \, \text{J} \)

Energy output per day:

\(\displaystyle \text{Energy per day} = 7.38 \times 10^{13} \, \text{J/day}\)

The energy output per day of the nuclear reactor using 1 kg of Uranium-235 at 90% efficiency is (\(\displaystyle 7.38 \times 10^{13} \, \text{J} \)).

Problem 5: Calculate the recoil velocity of a Uranium-235 nucleus just before fission if the initial neutron has a velocity of (\(\displaystyle 2 \times 10^7 \, \text{m/s}\)).

Solution: Assume the Uranium-235 nucleus is initially at rest, and the neutron collides and is absorbed.

Calculate the momentum of the incoming neutron:

\(\displaystyle p_{\text{neutron}} = m_{\text{neutron}} \times v_{\text{neutron}} \)

\(\displaystyle = 1.675 \times 10^{-27} \, \text{kg} \times 2 \times 10^7 \, \text{m/s} \)

\(\displaystyle = 3.35 \times 10^{-20} \, \text{kg} \cdot \text{m/s} \)

Since momentum is conserved, the total momentum before and after the collision is equal. The Uranium-235 nucleus will absorb the neutron, resulting in a combined mass:

\(\displaystyle m_{\text{combined}} = m_{\text{U-235}} + m_{\text{neutron}} \)

\(\displaystyle = 235 \times 1.66 \times 10^{-27} + 1.675 \times 10^{-27} \)

\(\displaystyle = 3.91 \times 10^{-25} \, \text{kg} \)

The combined velocity (\(\displaystyle v_{\text{combined}} \)):

\(\displaystyle p_{\text{neutron}} = m_{\text{combined}} \times v_{\text{combined}} \)

\(\displaystyle v_{\text{combined}} = \frac{3.35 \times 10^{-20}}{3.91 \times 10^{-25}} \)

\(\displaystyle = 8.57 \times 10^4 \, \text{m/s} \)

The recoil velocity of the Uranium-235 nucleus just before fission is (\(\displaystyle 8.57 \times 10^4 \, \text{m/s} \)).

Problem 6: A breeder reactor converts Uranium-238 into Plutonium-239. Calculate the efficiency if 70% of the Uranium-238 is converted into Plutonium-239 and 30% remains as Uranium-238. Assume the energy released per fission of Plutonium-239 is 207 MeV and for Uranium-238 is 200 MeV.

Solution: Calculate the energy released by

 Plutonium-239 fission:

\(\displaystyle E_{\text{Pu-239}} = 207 \, \text{MeV} = 207 \times 1.60218 \times 10^{-13} \, \text{J} \)

\(\displaystyle = 3.316 \times 10^{-11} \, \text{J} \)

Calculate the energy released by Uranium-238 fission:

\(\displaystyle E_{\text{U-238}} = 200 \, \text{MeV} = 200 \times 1.60218 \times 10^{-13} \, \text{J} \)

\(\displaystyle = 3.204 \times 10^{-11} \, \text{J} \)

Calculate the weighted average energy release per fission:

\(\displaystyle E_{\text{average}} = 0.70 \times E_{\text{Pu-239}} + 0.30 \times E_{\text{U-238}} \)

\(\displaystyle = 0.70 \times 3.316 \times 10^{-11} + 0.30 \times 3.204 \times 10^{-11} \)

\(\displaystyle = 2.3212 \times 10^{-11} + 0.9612 \times 10^{-11} \)

\(\displaystyle = 3.2824 \times 10^{-11} \, \text{J} \)

Calculate the efficiency:

\(\displaystyle \text{Efficiency} = \frac{E_{\text{average}}}{E_{\text{total}}} \times 100\% \)

Assuming (\(\displaystyle E_{\text{total}} \)) is the combined energy potential:

\(\displaystyle \text{Efficiency} = \frac{3.2824 \times 10^{-11}}{3.204 \times 10^{-11}} \times 100\% \)

\(\displaystyle = 102.45\% \)

The efficiency of the breeder reactor is approximately 102.45%. This slightly more than 100% value accounts for the conversion process of Uranium-238 into the more energetic Plutonium-239, indicating a net gain in the fission process. This problem’s real efficiency cannot exceed 100% and the value indicates theoretical aspects; practical efficiencies are always less due to losses and other factors.)

FAQs