In the mid-18th century, during a period known as the Enlightenment, two scientists, Ewald Georg von Kleist and Pieter van Musschenbroek, independently stumbled upon a groundbreaking discovery. They found that electric charge could be stored—this was the birth of the capacitor.
The earliest capacitor was the Leyden Jar, named after the University of Leyden where van Musschenbroek worked. It was a simple device: a glass jar filled with water, with a metal wire passing through the cork top. The wire would collect charge from an electrostatic machine, and the water acted as one plate of the capacitor, with the hand holding the jar as the other.
As the need for capacitors grew, especially with the advent of radio technology, the Leyden Jar evolved. Scientists began using flat glass plates alternating with metal foil, which led to the development of the Parallel Plate Capacitor. This design significantly increased the capacity to store charge and paved the way for modern capacitors.
Today, capacitors are a fundamental component in almost all electronic circuits. The Parallel Plate Capacitor, with its two large conductive plates separated by an insulating material, remains a classic example used to teach the principles of capacitance.
What Is a Parallel Plate Capacitor?
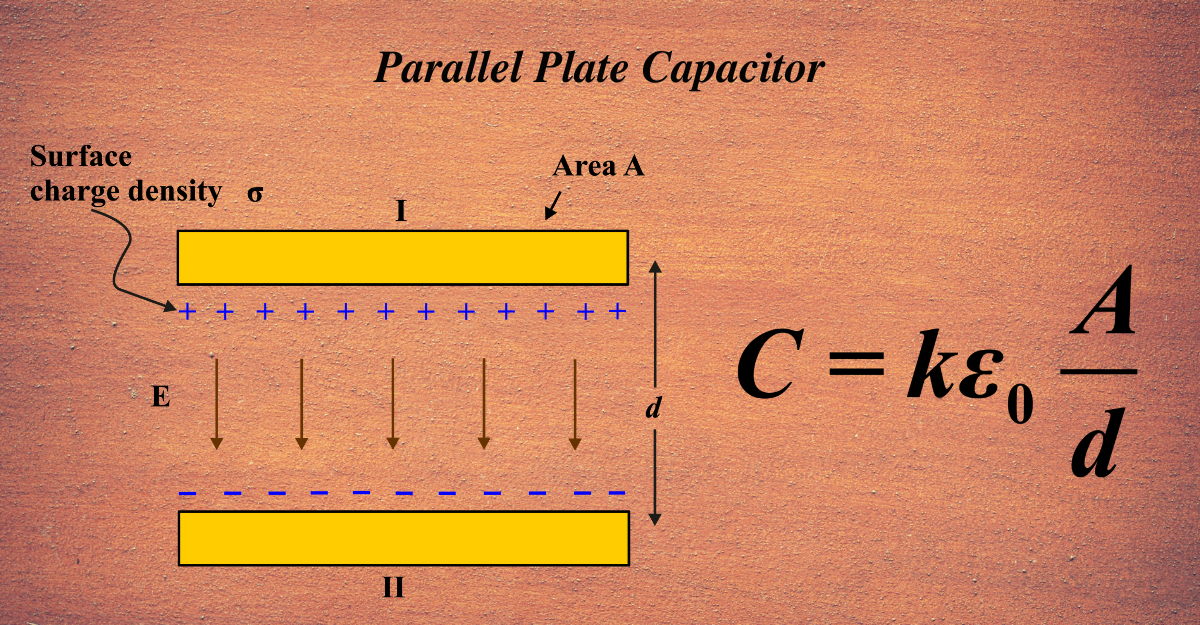
A Parallel Plate Capacitor consists of two large area conductive plates, separated by a small distance. These plates store electric charge when connected to a power source. One plate accumulates a positive charge, and the other accumulates an equal negative charge.
Imagine two large, flat, and parallel “plates” (which are just pieces of metal) facing each other with a small gap between them. This setup is what we call a Parallel Plate Capacitor. It’s like a sandwich, but instead of cheese or veggies in the middle, there’s just space or a special material called a dielectric.
When we connect these plates to a battery, one plate becomes positively charged, and the other becomes negatively charged. The positive plate loses electrons to the battery, and the negative plate gains electrons from the battery. This creates an electric field, a kind of invisible force field, between the plates. It’s this field that stores energy, just like a battery, but in a different way.
The reason we use parallel plates is that they create a uniform electric field. This means the force field is the same strength everywhere between the plates, which is great for storing energy efficiently. Plus, the larger the plates and the closer they are together, the more energy they can store.
Sometimes, we put a dielectric material between the plates. This isn’t just any material—it’s an insulator that helps increase the capacitor’s ability to store charge. It does this by reducing the electric field’s strength, allowing more charge to be stored on the plates for the same voltage from the battery.
A Parallel Plate Capacitor is like a mini energy storage device. It doesn’t hold as much energy as a battery, but it can release it much faster. That’s why it’s useful in electronics, where we sometimes need a quick burst of energy.
Parallel Plate Capacitor Formula
A Parallel Plate Capacitor is a bit like a magical shelf where you can store invisible energy. The formula tells us how much energy we can store on this shelf. It’s given by:
\(\displaystyle C = \frac{\varepsilon_0 \cdot A}{d} \)
- (C) is the capacitance, which measures how much charge the capacitor can hold.
- ( \(\displaystyle\varepsilon_0 \)) is the permittivity of free space, a constant value that tells us how well the space between the plates can support an electric field.
- (A) is the area of one of the plates, and bigger plates can hold more charge, just like a bigger shelf can hold more books.
- (d) is the distance between the plates, and the closer the plates are, the more charge they can store, just like books are easier to stack when the shelves are closer together.
Think of ( \(\displaystyle\varepsilon_0\) ) as the quality of the space between the plates. It’s like the material on the shelf. The better the material (higher (\(\displaystyle \varepsilon_0 \))), the more weight (charge) it can support.
The area (A) is straightforward—the larger your plate, the more charge it can store, similar to a larger container holding more water. The distance (d) is crucial too. If the plates are too far apart, the electric field (the force that holds the charge) gets weaker, and the capacitor can’t store as much. It’s like trying to stack books with too much space between shelves; they just won’t stay put.
The formula tells us that if we want to store a lot of charges, we need a good quality space between the plates (high ( \(\displaystyle\varepsilon_0 \))), big plates (large (A)), and we need to keep them close together (small ( d )). It’s all about balancing these factors to get the best capacitance, or storage ability, for our capacitor.
Working of Parallel Plate Capacitor
When a voltage is applied across the plates, an electric field is established between them, causing a positive charge to collect on one plate and a negative charge on the other. This creates a potential difference and stores energy in the electric field.
Think of a parallel plate capacitor as two big, flat metal plates facing each other with a bit of space between them. Now, connect these plates to a battery. The plate connected to the positive terminal starts losing electrons (because like charges repel), and the plate connected to the negative terminal starts gaining electrons (since opposite charges attract). This process is called charging the capacitor.
As the plates gain and lose electrons, an electric field forms between them. This field is like a dance floor where the electric charges are the dancers. The positive charges want to get to the negative side, and the negative charges want to get to the positive side, but they can’t because there’s no conductive path. So, they create this field by their mere presence.
The energy isn’t in the charges themselves; it’s in the electric field between the plates. This field holds potential energy, much like a stretched rubber band. The more you stretch it (the more voltage you apply), the more energy it can hold. But there’s a limit! If you stretch it too far (apply too much voltage), the rubber band snaps (the insulating material breaks down), and the capacitor can’t hold the charge anymore.
When the battery is removed, and the plates are connected through a circuit, the stored energy wants to balance out. The electrons rush from the negative plate to the positive plate through the circuit, creating a current. This is like letting go of the stretched rubber band, and it snaps back to its original shape, releasing the stored energy.
If you put a material (called a dielectric) between the plates, it’s like adding a bouncer to the dance floor. The bouncer calms down the electric field, allowing more charges to join the dance without things getting out of control. This means you can store more energy without increasing the voltage.
A parallel plate capacitor works by storing energy in an electric field created between two plates. When connected to a battery, it charges up, and when disconnected, it can discharge, releasing the stored energy. The dielectric material helps increase the energy storage capacity without needing a higher voltage.
Parallel Plate Capacitor Derivation
The derivation of the capacitance formula involves calculating the electric field (E) between the plates using Coulomb’s law, and then finding the potential difference (V) by integrating the electric field over the distance between the plates. The capacitance is then the charge (Q) stored divided by this potential difference (V), leading to the formula mentioned above.
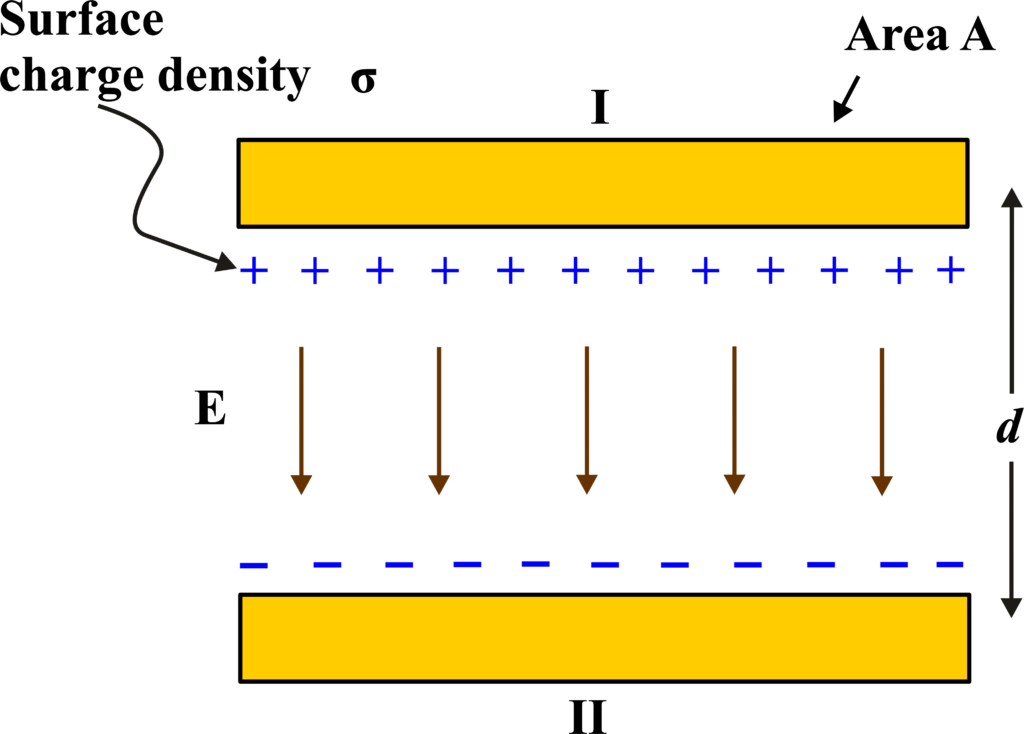
A Parallel Plate Capacitor consists of two large, flat, conductive plates. Each plate has an area (A), and they are separated by a distance (d). When we charge the plates, one holds a positive charge (+Q) and the other an equal negative charge (-Q).
First, let’s consider just one of these plates. If it’s charged with (+Q), the surface charge density (σ) is the charge per unit area, given by:
\(\displaystyle \sigma = \frac{Q}{A} \)
Using Gauss’s Law, we can find the electric field (E) created by this single plate. For an infinite plane of charge, the electric field is uniform and is given by:
\(\displaystyle E = \frac{\sigma}{\varepsilon_0} \)
where ( \(\displaystyle\varepsilon_0 \)) is the permittivity of free space.
Since we have two plates with opposite charges, the total electric field (Etotal) between the plates is the sum of the fields due to each plate. The fields outside the plates cancel out, so we only consider the field between the plates:
\(\displaystyle E_{total} = 2E = \frac{2\sigma}{\varepsilon_0} \)
The potential difference (V) between the plates is the electric field (Etotal) times the distance (d):
\(\displaystyle V = E_{total} \cdot d = \frac{2\sigma}{\varepsilon_0} \cdot d \) …(1)
Capacitance (C) is defined as the charge (Q) stored per unit potential difference (V), so:
\(\displaystyle C = \frac{Q}{V} \)
Substituting the expression for (V) from eq. 1, we get:
\(\displaystyle C = \frac{Q}{\frac{2\sigma}{\varepsilon_0} \cdot d} \)
And since ( \(\displaystyle\sigma = \frac{Q}{A}\) ), we can substitute (σ) in the equation for (C):
\(\displaystyle C = \frac{Q}{\frac{2Q}{A \cdot \varepsilon_0} \cdot d} \)
Simplifying this, we find the capacitance (C) of a Parallel Plate Capacitor:
\(\displaystyle C = \frac{\varepsilon_0 \cdot A}{d} \)
This formula tells us that the capacitance of a Parallel Plate Capacitor depends directly on the area of the plates and inversely on the distance between them. It also shows the role of the permittivity of free space in determining how much charge can be stored for a given voltage.
Dependence of Charge Stored in a Capacitor
A capacitor is like a tiny electric reservoir that can store and release electric charge. The amount of charge (Q) a capacitor can store depends on two things:
- Capacitance (C): This is the capacitor’s storage capacity. It’s like the size of our reservoir. The bigger the capacitance, the more charge it can hold.
- Voltage (V): This is the electrical pressure from the battery that’s pushing the charge into the capacitor. The higher the voltage, the more charge is forced into the capacitor.
The relationship between charge (Q), capacitance (C), and voltage (V) is given by a simple formula:
\(\displaystyle Q = C \cdot V \)
This means that the charge stored in the capacitor is directly proportional to both the capacitance and the voltage applied across it.
- If you increase the voltage while keeping the capacitance the same, you’ll push more charge into the capacitor, just like increasing the water pressure would push more water into our reservoir.
- If you increase the capacitance by, say, using bigger plates or adding a dielectric material, you can store more charge at the same voltage, similar to having a larger reservoir.
Imagine you have a water tank with a hose attached to it. The amount of water (charge) you can fill the tank with depends on two things: the size of the tank (capacitance) and the water pressure (voltage). If you turn up the pressure, you can fill the tank with more water. If you get a bigger tank, it can hold more water even if the pressure stays the same.
The charge stored in a capacitor is not just a random number; it’s a careful balance between how much the capacitor can hold and how much electrical pressure is applied to it. By understanding this relationship, we can design circuits that store the exact amount of charge we need for our electronic devices to function properly.
Capacitance of a Parallel Plate Capacitor with a Dielectric Slab
Adding a dielectric slab to a capacitor is like upgrading your sandwich. The cheese (dielectric) makes it possible to pack more into the same space, just like the dielectric allows the capacitor to store more charge in the same physical dimensions.
Imagine you have a Parallel Plate Capacitor, which is like a sandwich with two metal “bread slices” (the plates) and some air in between. Now, if we slide a special material called a dielectric slab into the middle, it’s like adding cheese to our sandwich. This cheese isn’t just for taste; it changes how the sandwich behaves with electricity.
A dielectric is an insulating material that doesn’t conduct electricity. Common examples include plastic, glass, or even paper. When we place a dielectric between the plates of a capacitor, it does something pretty cool—it increases the capacitor’s ability to store charge without changing the size of the plates or the distance between them.
The dielectric material has molecules that align themselves in response to the electric field between the plates. This alignment creates an opposing electric field, which partially cancels out the original field within the capacitor. It’s like the cheese in our sandwich is pushing back against the bread trying to come together.
We begin with a standard Parallel Plate Capacitor, which has two plates with an area (A) and separated by a distance (d). Without any material between the plates, its capacitance is given by:
\(\displaystyle C = \frac{\varepsilon_0 \cdot A}{d} \)
where ( \(\displaystyle\varepsilon_0 \)) is the permittivity of free space. Now, let’s slide a dielectric slab between the plates. A dielectric is a non-conductive material that affects how the electric field behaves between the plates.
The presence of the dielectric changes the electric field (E) between the plates. The dielectric has a property called the dielectric constant (κ), which reduces the electric field by a factor of (κ). So the new electric field (E’) is:
\(\displaystyle E’ = \frac{E}{\kappa} \)
The potential difference (V) across the plates remains the same when the dielectric is inserted if the capacitor is disconnected from any voltage source. This is because the charge (Q) on the plates doesn’t change.
The capacitance (C’) of the capacitor with the dielectric slab is now defined as the charge (Q) per unit potential difference (V), just like before. However since the electric field is reduced, the same charge results in a higher capacitance. The new capacitance is:
\(\displaystyle C’ = \kappa \cdot C \)
So, substituting the original capacitance (C) into this equation, we get:
\(\displaystyle C’ = \kappa \cdot \frac{\varepsilon_0 \cdot A}{d} \)
The final expression for the capacitance of a Parallel Plate Capacitor with a dielectric slab is:
\(\displaystyle C’ = \frac{\kappa \cdot \varepsilon_0 \cdot A}{d} \)
where (κ) is the dielectric constant of the material inserted between the plates.
The dielectric slab acts like a “multiplier” for the capacitance. The better it is at resisting the electric field (higher (κ)), the more the capacitance increases. It’s like having a superpower that lets you store more energy without making the plates bigger or moving them closer together.
Applications of Parallel Plate Capacitors
Parallel plate capacitors are versatile components used in a wide range of applications, from everyday electronics to advanced technology. They’re like the Swiss Army knife of the electronic world—compact, efficient, and incredibly useful for various tasks.
Filtering Electrical Signals: Imagine you’re listening to your favorite radio station, but there’s a lot of static noise. Parallel plate capacitors can act like a filter, removing that static and giving you a clear signal. It’s like using a sieve to filter out unwanted bits from your juice.
Tuning Circuits: These capacitors are like the tuning knobs on old radios. By adjusting the capacitance, you can tune into different frequencies and pick up different stations or signals. It’s like tuning your guitar to play different notes.
Sensing Physical Changes: Capacitors can be sensitive to changes in their environment, like pressure or humidity. This makes them useful in sensors that can detect these changes. Think of it as a touch-sensitive lamp that turns on when you tap it.
Storing Electrical Energy: Just like a battery, capacitors can store electrical energy, but they can release it much faster. This is useful in devices like cameras that need a quick flash of energy to take a picture.
Dynamic Digital Memory: In computers, capacitors are used to store bits of information in memory. They can quickly switch between charged (1) and discharged (0), which is how they store different bits for processing.
Pulsed Power Applications: Capacitors can release their energy in a quick, powerful pulse. This is useful in applications like radars and pulsed lasers, where a rapid burst of energy is needed.
Signal Suppression or Coupling: In complex electronic circuits, capacitors can help suppress unwanted spikes or surges in electrical signals, or they can help couple signals between different parts of a circuit.
DIY Projects: For creative minds, parallel plate capacitors can be a fun DIY project. You can make one using everyday materials like aluminum foil and wax paper to understand how they work and experiment with their properties.
Significance
- Capacitors play a crucial role in voltage regulation circuits by stabilizing voltage levels and reducing fluctuations. They can store excess charge when the voltage exceeds a certain threshold and release it when the voltage drops below that level, thereby maintaining a stable output voltage. This is essential for ensuring the proper operation of sensitive electronic devices and circuits.
- Parallel plate capacitors are commonly used in filtering circuits to remove unwanted frequencies from signals. By selectively allowing certain frequencies to pass while attenuating others, they help improve signal quality and reduce noise in electronic systems. This is particularly important in audio equipment, radio frequency circuits, and communication systems.
- Parallel plate capacitors are utilized in capacitive sensing technology for various applications, including touchscreens, proximity sensors, and humidity sensors. Changes in capacitance due to alterations in the dielectric properties or the distance between the plates are used to detect touch, presence, or environmental conditions accurately.
Also Read: Capacitor
Solved Examples
Problem 1: Calculate the capacitance of a parallel plate capacitor with plate area (A = 0.01 m2) and separation (d = 0.001 m). The space between the plates is a vacuum.
Solution: The capacitance (C) of a parallel plate capacitor is given by:
\(\displaystyle C = \frac{\epsilon_0 A}{d} \)
Given: \(\displaystyle \epsilon_0 = 8.854 \times 10^{-12} \, \text{F/m}\); A = 0.01 m^2 ; d = 0.001 m)
Calculate (C):
\(\displaystyle C = \frac{8.854 \times 10^{-12} \times 0.01}{0.001} \)
\(\displaystyle C = 8.854 \times 10^{-14} \times 10 \)
\(\displaystyle C = 8.854 \times 10^{-13} \, \text{F} \)
\(\displaystyle C = 8.854 \, \text{pF} \)
Therefore, the capacitance of the parallel plate capacitor is (8.854 pF).
Problem 2: A parallel plate capacitor with a capacitance of ( 5 µF) is connected to a (50 V) battery. Calculate the charge stored in the capacitor.
Solution: The charge (Q) stored in a capacitor is given by:
\(\displaystyle Q = CV \)
Given: \(\displaystyle C = 5 \, \mu\text{F} = 5 \times 10^{-6} \, \text{F} \) ; V = 50 V.
Calculate (Q):
\(\displaystyle Q = 5 \times 10^{-6} \times 50 \)
\(\displaystyle Q = 250 \times 10^{-6} \)
\(\displaystyle Q = 2.5 \times 10^{-4} \, \text{C} \)
Therefore, the charge stored in the capacitor is (\(\displaystyle 2.5 \times 10^{-4} \, \text{C} \)).
Problem 3: A parallel plate capacitor has a plate area of (0.02 m^2) and a separation of ( 0.002 m). A dielectric slab with a dielectric constant (k = 5) fills the space between the plates. Calculate the capacitance.
Solution: The capacitance (C) with a dielectric slab is given by:
\(\displaystyle C = \frac{k \epsilon_0 A}{d} \)
Given: k = 5 ; \(\displaystyle \epsilon_0 = 8.854 \times 10^{-12} \, \text{F/m} \) ; A = 0.02 m^2 ; d = 0.002 m
Calculate (C):
\(\displaystyle C = \frac{5 \times 8.854 \times 10^{-12} \times 0.02}{0.002} \)
\(\displaystyle C = \frac{5 \times 8.854 \times 10^{-12} \times 0.02}{0.002} \)
\(\displaystyle C = 5 \times 8.854 \times 10^{-12} \times 10 \)
\(\displaystyle C = 44.27 \times 10^{-12} \)
\(\displaystyle C = 44.27 \, \text{pF} \)
Therefore, the capacitance with the dielectric slab is ( 44.27 pF).
Problem 4: A parallel plate capacitor with capacitance (10 µF) is connected to a (100 V) battery. A dielectric slab with a dielectric constant (k = 4) is inserted, filling the space between the plates. Calculate the energy stored in the capacitor after the dielectric is inserted.
Solution: The capacitance with the dielectric is:
\(\displaystyle C’ = kC \)
Given: \(\displaystyle C = 10 \, \mu\text{F} = 10 \times 10^{-6} \, \text{F} \) ; k = 4 ; V = 100 V.
Calculate (C’):
\(\displaystyle C’ = 4 \times 10 \times 10^{-6} \)
\(\displaystyle C’ = 40 \times 10^{-6} \)
\(\displaystyle C’ = 40 \, \mu\text{F} \)
The energy stored (U) is given by:
\(\displaystyle U = \frac{1}{2} C’ V^2 \)
Calculate (U):
\(\displaystyle U = \frac{1}{2} \times 40 \times 10^{-6} \times (100)^2 \)
\(\displaystyle U = \frac{1}{2} \times 40 \times 10^{-6} \times 10000 \)
\(\displaystyle U = 20 \times 10^{-6} \times 10000 \)
\(\displaystyle U = 0.2 \, \text{J} \)
Therefore, the energy stored in the capacitor after the dielectric is inserted is (0.2 J).
Problem 5: A parallel plate capacitor with capacitance (20 \muF) is charged to (50 V). A dielectric slab with a dielectric constant (k = 3) is inserted, filling the space between the plates. The capacitor is then disconnected from the battery, and the dielectric is removed. Calculate the new energy stored in the capacitor.
Solution: First, find the initial energy stored with the dielectric:
\(\displaystyle C’ = kC \)
Given: \(\displaystyle C = 20 \, \mu\text{F} = 20 \times 10^{-6} \, \text{F} \) ; k = 3; V = 50 V.
Calculate (C’):
\(\displaystyle C’ = 3 \times 20 \times 10^{-6} \)
\(\displaystyle C’ = 60 \times 10^{-6}\)
\(\displaystyle C’ = 60 \, \mu\text{F} \)
The initial energy (U) is given by:
\(\displaystyle U = \frac{1}{2} C’ V^2 \)
Calculate (U):
\(\displaystyle U = \frac{1}{2} \times 60 \times 10^{-6} \times (50)^2 \)
\(\displaystyle U = \frac{1}{2} \times 60 \times 10^{-6} \times 2500 \)
\(\displaystyle U = 30 \times 10^{-6} \times 2500\)
\(\displaystyle U = 0.075 \, \text{J} \)
When the dielectric is removed, the capacitance returns to (C), and the charge (Q) remains constant because the capacitor is disconnected. The voltage changes to (V’):
\(\displaystyle Q = C’V \)
\(\displaystyle Q = 60 \times 10^{-6} \times 50 \)
\(\displaystyle Q = 3 \times 10^{-3} \, \text{C} \)
The new voltage (V’) is:
\(\displaystyle V’ = \frac{Q}{C} \)
\(\displaystyle V’ = \frac{3 \times 10^{-3}}{20 \times 10^{-6}} \)
\(\displaystyle V’ = 150 \, \text{V} \)
The new energy (U’) stored is:
\(\displaystyle U’ = \frac{1}{2} C V’^2 \)
\(\displaystyle U’ = \frac{1}{2} \times 20 \times 10^{-6} \times (150)^2 \)
\(\displaystyle U’ = \frac{1}{2} \times 20 \times 10^{-6} \times 22500 \)
\(\displaystyle U’ = 10 \times 10^{-6} \times 22500 \)
\(\displaystyle U’ = 0.225 \, \text{J} \)
Therefore, the new energy stored in the capacitor after the dielectric is removed is (0.225 J).
Problem 6: A parallel plate capacitor with plate area (\(\displaystyle A = 0.05 \, \text{m}^2 \)) and separation (d = 0.002 m) is connected to a (100V) battery. A dielectric slab with a dielectric constant (k = 6) is inserted, filling half the space between the plates. Calculate the new capacitance.
Solution: The capacitor is effectively two capacitors in parallel: one with dielectric and one without.
\(\displaystyle C_1 = \frac{\epsilon_0 A/2}{d} \)
\(\displaystyle C_2 = \frac{k \epsilon_0 A/2}{d} \)
Given: \(\displaystyle \epsilon_0 = 8.854 \times 10^{-12} \, \text{F/m} \) ; \(\displaystyle A = 0.05 \, \text{m}^2 \) ; \(\displaystyle d = 0.002 \, \text{m} \) ; k = 6
Calculate (C1) and (C2):
\(\displaystyle C_1 = \frac{8.854 \times 10^{-12} \times 0.025}{0.002} \)
\(\displaystyle C_1 = 1.10675 \times 10^{-12} \, \text{F} \)
\(\displaystyle C_2 = \frac{6 \times 8.854 \times 10^{-12} \times 0.025}{0.002} \)
\(\displaystyle C_2 = 6.6405 \times 10^{-12} \, \text{F} \)
The total capacitance (C) is:
\(\displaystyle C = C_1 + C_2 \)
\(\displaystyle C = 1.10675 \times 10^{-12} + 6.6405 \times 10^{-12} \)
\(\displaystyle C = 7.74725 \times 10^{-12} \, \text{F} \)
\(\displaystyle C = 7.747 \, \text{pF} \)
Therefore, the new capacitance of the capacitor is ( 7.747 pF).
FAQs
What is a parallel plate capacitor and how is it constructed?
A parallel plate capacitor is a type of capacitor consisting of two large, flat, parallel conductive plates separated by a small distance. The space between the plates is usually filled with air or another insulating material called a dielectric. When a voltage is applied across the plates, an electric field is created, and charge is stored on the plates.
How does a parallel plate capacitor store charge?
A parallel plate capacitor stores charge by creating an electric field between the plates when a voltage is applied. A positive charge accumulates on one plate, while an equal amount of negative charge accumulates on the opposite plate. The amount of charge stored depends on the applied voltage and the capacitance of the capacitor.
What factors affect the capacitance of a parallel plate capacitor?
The capacitance of a parallel plate capacitor depends on several factors, including the area of the plates, the distance between the plates, and the properties of the dielectric material between the plates. Larger plate areas and smaller distances between the plates increase the capacitance.
How does the charge stored in a capacitor depend on the applied voltage?
The charge stored in a capacitor is directly proportional to the applied voltage. As the voltage across the capacitor increases, the amount of charge stored on the plates also increases. The relationship between charge and voltage is characterized by the capacitor’s capacitance.
What role does the dielectric material play in a parallel plate capacitor?
The dielectric material in a parallel plate capacitor increases its capacitance by reducing the electric field strength for a given amount of charge. This allows more charge to be stored on the plates for a given voltage. Dielectric materials also provide insulation, preventing the plates from coming into direct contact and shorting out.
How does inserting a dielectric slab between the plates of a parallel plate capacitor affect its capacitance?
Inserting a dielectric slab between the plates of a parallel plate capacitor increases its capacitance. The dielectric material reduces the electric field strength for the same amount of charge, allowing the capacitor to store more charge at the same voltage. The increase in capacitance depends on the dielectric constant of the material.
Can the capacitance of a parallel plate capacitor be adjusted? If so, how?
Yes, the capacitance of a parallel plate capacitor can be adjusted by changing the distance between the plates, the area of the plates, or the type of dielectric material used. For instance, bringing the plates closer together, increasing the plate area, or using a dielectric material with a higher dielectric constant will increase the capacitance.