Pascal’s law

Pascal’s Law states that when pressure is applied to a confined fluid, the pressure change occurs throughout the entire fluid equally and in all directions. This means that any external pressure on a fluid in a closed system will be felt equally at every point in that fluid.

In the mid-17th century, a brilliant French mathematician and physicist named Blaise Pascal began exploring the secrets of fluid mechanics. His curiosity and rigorous experiments led him to a groundbreaking discovery that would change the way we understand the behavior of fluids.

Blaise Pascal was not just a scientist; he was a child prodigy, an inventor, and a philosopher. Born in 1623, Pascal was fascinated by the natural world and the principles that governed it. His work spanned various fields, but it was his interest in hydrostatics that led to the formulation of the law we study today.

Legend has it that Pascal’s Law was inspired by an experiment involving a barrel filled with water. Pascal inserted a long, narrow tube into the barrel and poured water into the tube. To his amazement, the pressure exerted by the water in the tube caused the barrel to burst. This observation led Pascal to realize that pressure applied to a confined fluid is transmitted undiminished in all directions¹.

In 1653, Pascal published his findings in a book titled “The Physical Treatises of Pascal.” This work included his observations on the principles of static fluids. He noted that pressure in a fluid at rest is the same at all points if these points are at the same depth, and if we apply external pressure to this fluid, all the applied force is distributed throughout the liquid.

Pascal’s Law laid the foundation for what we now call fluid mechanics. It’s a principle that finds applications in many modern technologies, such as hydraulic lifts and brakes. Pascal’s insights have allowed us to harness the power of fluids to perform work that would otherwise be impossible.

What is Pascal’s Law?

Imagine you’re playing with a water balloon. When you squeeze it, the water inside doesn’t just move in one direction; it pushes out evenly in all directions. This is similar to what happens in Pascal’s Law.

Pascal’s Law tells us that when we apply pressure to any point of a confined fluid (like water in a balloon or oil in a hydraulic system), this pressure is transmitted equally throughout the fluid. This means that no matter where you apply the pressure, every part of the fluid feels the same amount of pressure increase.

Think of a tube of toothpaste. When you press on one end, the paste comes out the other end. You’re applying pressure at one point, but that pressure moves through the entire tube and pushes the paste out evenly.

The reason this happens is that fluids are not easily compressed. So, when you apply pressure, the fluid can’t just “squish” together; it has to go somewhere. And since the fluid is enclosed, it pushes back equally in all directions.

Imagine you have a syringe filled with water, and you’re trying to push the plunger down. The force you apply with your hand is transmitted through the water to the other end. This is where Pascal’s Law comes into play, and it’s described by a very straightforward formula:

\(\displaystyle P = \frac{F}{A} \)

• (P) stands for pressure—it’s like the push or squeeze you feel in the water when you try to compress it.
• (F) represents the force you’re applying on the plunger of the syringe.
• (A) is the area of the plunger’s end where you’re applying the force.

The formula tells us that the pressure (P) in a fluid is equal to the force (F) applied, divided by the area (A) over which the force is distributed. It’s like having a big and a small water balloon; if you squeeze them with the same force, the smaller one will feel a stronger pressure because the area is smaller.

This formula is super important because it explains how hydraulic machines work. For example, in a hydraulic lift, a small force applied on a small piston can create a big force on a larger piston, just because the area of the larger piston is bigger.

This law is fundamental in understanding how hydraulic systems work, like the brakes in your car or an elevator lift. It’s all about how pressure in a fluid can be used to do work and move things!

Pascal’s Law Derivation

Imagine you have a tiny, right-angled triangular block (like a piece of cheese) submerged in a glass of water. This block is our prismatic triangle, and it’s so small that every point on it is at the same depth.

Because our prismatic triangle is so small and at the same depth, the pressure from the water is the same all over it. It’s like being gently squeezed by an evenly spread hand.

Gravity pulls on everything equally at this depth, so our tiny triangle feels the same force of gravity no matter where you look at it.

Pascal’s Law tells us that pressure in a fluid at rest is the same in all directions. So, for our little triangle, this means that no matter which side you’re looking at—the long side, the short side, or the hypotenuse—the pressure pushing on that side is the same.

This principle is super important because it explains how things like hydraulic lifts work. Just like the uniform pressure on our triangle, a hydraulic lift uses fluid pressure to lift heavy objects evenly without tilting or tipping them.

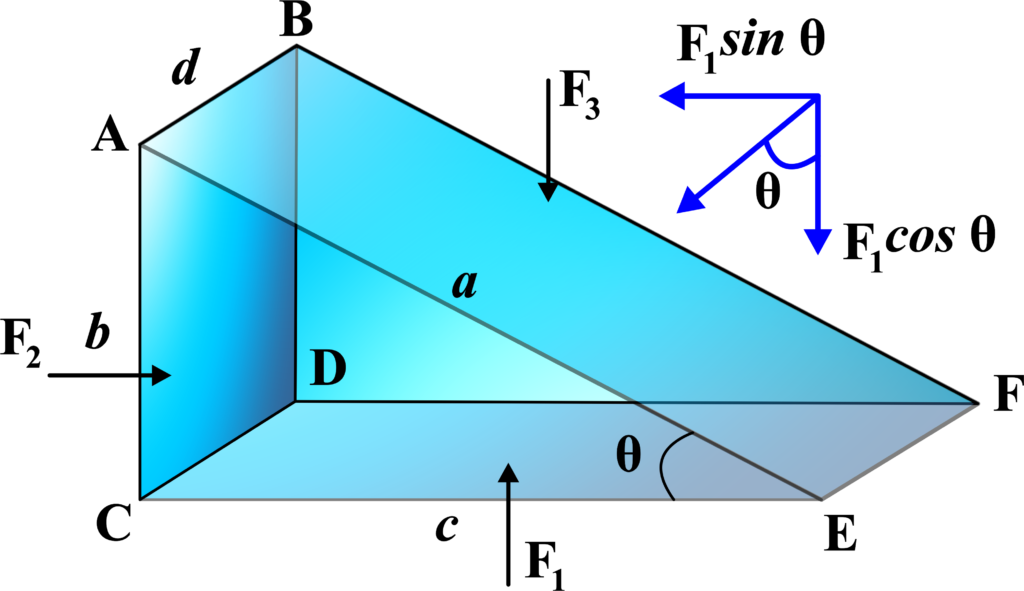
Pascal’s Law is all about how pressure in a fluid stays even and consistent, no matter where you are in that fluid. And for our prismatic triangle, it means that it’s experiencing the same squeeze from the water all around, just like you’d feel the same squeeze from all sides if you were deep underwater.

To derive Pascal’s Law, consider a small element of fluid in equilibrium. The forces due to pressure at any point within the fluid must balance out in all directions. Since the fluid is at rest, the net force must be zero, concluding that the pressure must be the same at all points at the same depth.

• A right-angled prismatic triangle submerged in a liquid of density (ρ).
• The prismatic element is small, so all points are at the same depth and experience the same gravitational effect.
• Areas of the faces are (ad), (bd), and (cd) for faces ABFE, ABDC, and CDFE, respectively.
• Pressures on the faces are (P₁), (P₂), and (P₃).
• Forces exerted by the pressures are (F₁), (F₂), and (F₃) on their respective faces.

To show that the pressures (P₁), (P₂), and (P₃) are equal, demonstrating Pascal’s Law. The forces due to pressure are normal to the surface. Therefore, we can write the forces as:

\(\displaystyle F_1 = P_1 \cdot ad \hspace{1cm}\text{ area of ABFE}\)

\(\displaystyle F_2 = P_2 \cdot bd \hspace{1cm}\text{area of ABDC} \)

\(\displaystyle F_3 = P_3 \cdot cd \hspace{1cm}\text{area of CDFE}\)

Since the prismatic element is at rest and submerged in a fluid at equilibrium, the net force in any direction must be zero.

For the prismatic element to be in equilibrium, the forces along each axis (let’s say x and y) must balance out. This gives us two equations:

• Along x-axis: \(\displaystyle F_1 \cos(\theta) = F_3\)
• Along the y-axis: \(\displaystyle F_1 \sin(\theta) = F_2\) where (θ) is the angle between face ABFE and the horizontal.

Replace (F₁), (F₂), and (F₃) with their expressions in terms of pressure and area:

\(\displaystyle P_1 \cdot ad \cos(\theta) = P_3 \cdot cd\)

\(\displaystyle P_1 \cdot ad \sin(\theta) = P_2 \cdot bd\)

From the above equations, we can solve for (P₁), (P₂), and (P₃):

\(\displaystyle P_3 = P_1 \cdot \frac{ad}{cd} \cos(\theta)\)

\(\displaystyle P_2 = P_1 \cdot \frac{ad}{bd} \sin(\theta)\)

Since the prismatic triangle is right-angled, (ad), (bd), and (cd) are related by Pythagoras’ theorem, and \(\displaystyle\cos(\theta)\) and \(\displaystyle\sin(\theta)\) are related to these sides.

After simplifying, we find that (P₁ = P₂ = P₃), which confirms Pascal’s Law that pressure at a point in a fluid at rest is the same in all directions.

This derivation shows that within a small element of fluid at the same depth, the pressure is uniform and does not depend on the orientation of the surface upon which it acts. This is Pascal’s Law, and it’s fundamental to understanding how fluids transmit force in systems like hydraulic lifts or brakes.

Variation of Pressure with Depth

The pressure within a fluid increases with depth due to the weight of the fluid above.

Imagine you’re swimming in the ocean. As you dive deeper, you can feel the water pressing harder against your body. This is because the deeper you go, the more water there is above you, and thus, the greater the weight that exerts pressure on you.

The pressure at any point in a fluid, like water or air, depends on the depth of that point. At the surface, the pressure is just the atmospheric pressure, but as you go deeper, the pressure increases because of the weight of the fluid above that point.

The pressure variation with depth in a fluid can be described by the formula:

\(\displaystyle P = P_0 + \rho g h \)

• (P) is the pressure at depth,
• (P₀) is the atmospheric pressure at the surface,
• (ρ) is the density of the fluid,
• (g) is the acceleration due to gravity,
• (h) is the depth below the surface.
• Atmospheric Pressure (P₀): This is the pressure exerted by the air above the fluid. It’s what we feel all the time.
• Density (ρ): This tells us how much mass there is in a given volume of the fluid. The denser the fluid, the higher the pressure with depth.
• Acceleration Due to Gravity (g): This is the force of gravity that pulls the fluid downwards, contributing to the pressure.
• Depth (h): The deeper you go, the more fluid is above you, and hence, the greater the pressure.

When you’re at the bottom of a swimming pool, the pressure you feel is not just because of the water but also the air above the water. That’s why even a short dive can make your ears pop!

The “Variation of Pressure with Depth” tells us that the deeper you go into a fluid, the more pressure you’ll feel, and it’s all because of the weight of the fluid above you.

As you go deeper into a fluid, the pressure increases. This is because there’s more fluid above you, and its weight adds to the pressure exerted on you. This increase in pressure is uniform; it doesn’t matter if you’re in the middle of the ocean or a narrow tube, the pressure will increase at the same rate as you go deeper.

At the surface, the pressure you feel is mostly atmospheric pressure. But once you’re submerged, the water’s pressure starts to add up. Scuba divers need to be aware of this variation because it affects their buoyancy and the risk of decompression sickness.

Engineers must consider this pressure variation when designing structures like dams or submarines to ensure they can withstand the increased pressure at greater depths. You can feel this pressure increase even when you dive to the bottom of a swimming pool; your ears might pop due to the change in pressure.

In many activities that involve depth, like diving or underwater construction, safety measures are in place to deal with the increasing pressure.

Applications of Pascal’s Law

Hydraulic Lifts

Hydraulic Lifts are used to lift heavy objects by applying force to a small piston, which is then transmitted to a larger piston. Imagine you have a small water pistol. When you push the tiny piston, water shoots out with a lot of force. Now, think of a hydraulic lift as a giant version of that water pistol, but instead of shooting water, it lifts heavy objects like cars.

A hydraulic lift operates on the principle of Pascal’s Law, which states that pressure applied to a confined fluid is transmitted equally throughout the fluid¹. This means that if you apply pressure at one point in a fluid, that same pressure can be used to push something else at another point.

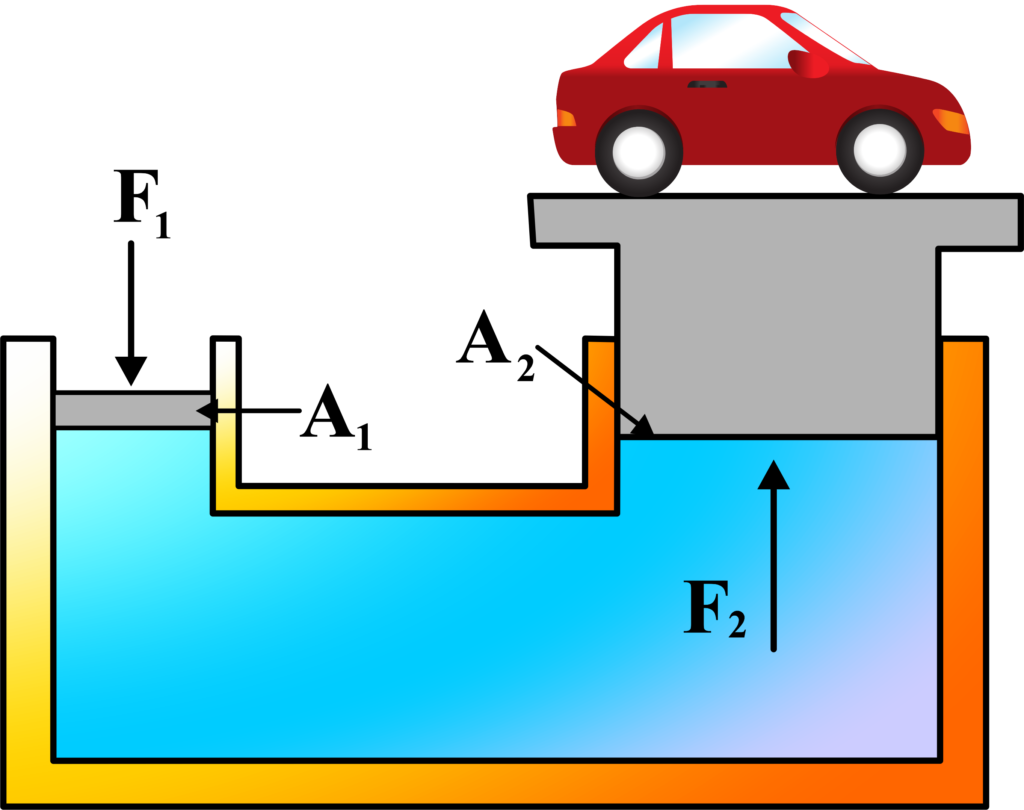
In a hydraulic lift, you have two pistons: a small one and a large one, connected by a pipe and filled with an incompressible fluid, usually oil. The small piston is where you apply a small force, and the large piston is where you get a large force output.

When you apply a force to the small piston, that force is transmitted through the oil to the large piston. Because the large piston has a bigger area, the force coming out is much larger. This is how a small force can lift something as heavy as a car.

Think of a car repair shop. The mechanic uses a hydraulic lift to raise cars for inspection. The mechanic applies a small force to the small piston, and the car is lifted by the large piston. It’s all thanks to the even transmission of pressure through the fluid.

The key point here is that the force is multiplied by the difference in the size of the pistons. This is why hydraulic lifts are so powerful and widely used in industries to lift heavy loads with minimal effort.

Derivation

A hydraulic lift consists of two pistons connected by a pipe and filled with an incompressible fluid. One piston is small, and the other is large. According to Pascal’s Law, pressure applied to a confined fluid is transmitted equally throughout the fluid.

The pressure (P) exerted by a force (F) on a piston with area (A) is given by:

\(\displaystyle P = \frac{F}{A} \)

Applying the Law to Both Pistons

• (F₁) as the force is applied to the small piston,
• (A₁) as the area of the small piston,
• (F₂) as the force exerted by the large piston,
• (A₂) as the area of the large piston.

According to Pascal’s Law, the pressure (P) is the same for both pistons:

\(\displaystyle P = \frac{F_1}{A_1} = \frac{F_2}{A_2} \)

To find the force exerted by the large piston (F₂), we rearrange the equation:

\(\displaystyle F_2 = P \times A_2 \)

Substituting (P) from the small piston’s equation, we get:

\(\displaystyle F_2 = \frac{F_1}{A_1} \times A_2 \)

The ratio of the force exerted by the large piston to the force applied on the small piston gives us the mechanical advantage (MA) of the hydraulic lift:

\(\displaystyle MA = \frac{F_2}{F_1} = \frac{A_2}{A_1} \)

This means that the force exerted by the large piston is \(\displaystyle \frac{A_2}{A_1} \) times the force applied on the small piston. The derived expression shows how a hydraulic lift can amplify a small input force into a much larger output force, allowing heavy objects to be lifted with relatively little effort.

Hydraulic Brakes

In vehicles, a small force applied at the brake pedal is transmitted through brake fluid to exert a larger force on the brake pads.

When a vehicle suddenly hits the brakes while moving, there’s a risk of skidding because the wheels don’t slow down uniformly. To prevent this danger, we need a brake system that ensures each wheel slows down equally and at the same time. That’s where hydraulic brakes come in. They work based on Pascal’s law, which states that pressure applied to a fluid in a closed system is transmitted equally in all directions.

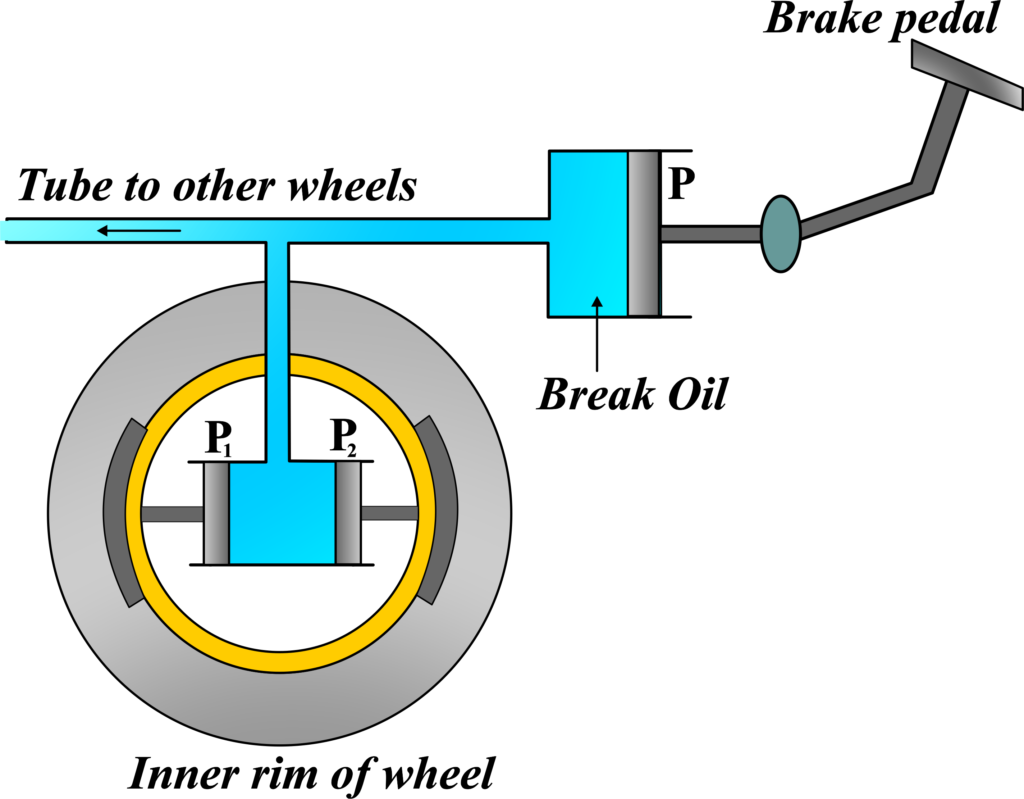
Now, let’s understand how a hydraulic brake system works with an example. Imagine a car’s brake system with a main cylinder filled with brake oil. Inside this cylinder, there’s a piston connected to the brake pedal. When you press the brake pedal, this piston is pushed, increasing the pressure in the main cylinder. At the other end of the main cylinder, there’s a T-shaped tube connected to the wheel cylinder.

The wheel cylinder contains two smaller pistons, P₁ and P₂, which are connected to brake shoes, S1 and S2, respectively. When the brake pedal is pressed, the pressure from the main cylinder is transmitted to pistons P₁ and P₂. These pistons then push the brake shoes away from each other, causing them to press against the inner rim of the wheel. As a result, the motion of the wheel is arrested, and the vehicle slows down.

What’s interesting is that the area of pistons P₁ and P₂ is larger than that of the piston connected to the brake pedal. This means that even though you apply a small force to the brake pedal, it produces a much larger force on the wheel rim, allowing for effective braking. Additionally, the main cylinder is connected to all the wheels of the vehicle through a pipeline, ensuring that equal pressure is applied to all the wheels simultaneously, preventing uneven braking and potential skidding.

Because the pressure is transmitted equally, each wheel receives the same braking force, ensuring the car stops smoothly and straight. A small force applied at the brake pedal is multiplied, allowing a much greater force to be applied to the brakes with minimal effort. Hydraulic brakes are reliable and responsive, providing safety in various driving conditions. This way, hydraulic brakes help keep vehicles safe on the road.

Hydraulic Press

Hydraulic presses are used in manufacturing to mold or shape materials by applying a small force to achieve a greater output force.

Think of a hydraulic press as a super-strong version of a nutcracker. Just like you use a nutcracker to apply a small force to crack open a tough nut, a hydraulic press uses a small force to lift or compress very heavy objects.

A hydraulic press consists of two connected cylinders, each fitted with a piston. The cylinders are filled with an incompressible fluid, typically oil. One cylinder is larger than the other, and this is key to how the press works.

Pascal’s Law states that pressure applied to a confined fluid is transmitted equally throughout the fluid. In the case of the hydraulic press, when you apply a force to the smaller piston, that force is transmitted through the fluid to the larger piston.

Because the larger piston has a greater area, the force that it exerts is proportionally larger. This means that a small force applied to the small piston can result in a much larger force exerted by the large piston.

Hydraulic presses are used in car manufacturing to shape metal parts. A worker applies a small force to operate the press, and the large piston exerts a massive force to mold or cut the metal into the desired shape.

The hydraulic press is a powerful demonstration of Pascal’s Law in action. It shows how physics allows us to perform tasks that would be impossible with our strength alone. By understanding how a hydraulic press works, students can see the practical applications of the concepts they learn in class and how they enable modern manufacturing processes.

Also Read: What is Pressure?

Limitations of Pascal’s Law

Pascal’s Law is incredibly useful and applies to many situations, but like all scientific principles, it has its limitations.

• Requires a Confined Fluid: Pascal’s Law works for fluids that are confined within a container or a system. If the fluid can flow freely and isn’t confined, the law doesn’t apply because the pressure won’t be transmitted undiminished.
• Incompressible Fluids: The law assumes that the fluid is incompressible. In real-life applications, most fluids compress to some degree under high pressure, which can affect the transmission of pressure.
• No External Forces: Pascal’s Law assumes that no additional external forces are acting on the fluid other than the pressure being applied. In reality, factors like gravity and friction can influence how pressure is transmitted through a fluid.
• Steady Conditions: The law is based on static conditions, meaning the fluid must be at rest. If the fluid is moving or if there are changes in the fluid’s flow or velocity, Pascal’s Law doesn’t hold because the dynamics of fluid motion come into play.
• Homogeneous Fluid: Pascal’s Law assumes the fluid is homogeneous in nature. If there are variations in the fluid’s composition or temperature, this can lead to differences in pressure transmission.
• No Viscosity Effects: The law does not take into account the viscosity of the fluid. Viscosity, or the fluid’s resistance to flow, can affect how pressure is applied and transmitted in a fluid system.
• Ideal Conditions: Pascal’s Law is an idealization. In practical applications, things like the elasticity of the container walls, the presence of air bubbles, or impurities in the fluid can all cause deviations from the ideal behavior predicted by Pascal’s Law.

Solved Examples

Example 1: A scuba diver descends to a depth of (20 m) in the ocean. Calculate the increase in pressure experienced by the diver due to the depth. (Assume the density of seawater to be (1025 kg/m³) and (g = 9.8 m/s²)

Solution: The increase in pressure with depth can be calculated using the formula:

\(\displaystyle \Delta P = \rho g h \)
\(\displaystyle \Delta P = 1025 \times 9.8 \times 20 \)
\(\displaystyle \Delta P = 200900 \, \text{Pa} \)

So, the increase in pressure experienced by the diver is (200900 Pa).

Example 2: A hydraulic lift has a small piston with a diameter of (5 cm) and a large piston with a diameter of (50 cm). If a force of (1000 N) is applied to the small piston, calculate the force exerted by the large piston.

Solution: Using Pascal’s law, the ratio of force exerted by the large piston (F₂) to the force exerted by the small piston (F₁) is equal to the ratio of the areas of the pistons:

\(\displaystyle \frac{F_2}{F_1} = \frac{A_2}{A_1} \)
\(\displaystyle F_2 = \frac{A_2}{A_1} \times F_1 \)
\(\displaystyle F_2 = \frac{\pi \times (0.5)^2}{\pi \times (0.05)^2} \times 1000 \)
\(\displaystyle F_2 = \frac{2500}{0.0025} \times 1000 \)
\(\displaystyle F_2 = 100000N \)

So, the force exerted by the large piston is (100000 N).

Example 3: A hydraulic press has a small piston with a diameter of (5 cm) and a large piston with a diameter of (30 cm). If a force of (2000 N) is applied to the small piston, calculate the force exerted by the large piston.

Solution: Using Pascal’s law, the force exerted by the large piston can be calculated using the same formula as in Example 2:

\(\displaystyle F_2 = \frac{A_2}{A_1} \times F_1 \)
\(\displaystyle F_2 = \frac{\pi \times (0.15)^2}{\pi \times (0.025)^2} \times 2000 \)
\(\displaystyle F_2 = \frac{6750}{0.000625} \times 2000 \)
F₂ = 2.16×10¹⁰ N

So, the force exerted by the large piston is (2.16×10¹⁰ N).

FAQs