The story of the photoelectric effect begins in the late 19th century. In 1887, Heinrich Hertz discovered that ultraviolet light could cause sparks to jump between two metal electrodes. Wilhelm Hallwachs followed up on Hertz’s work and found that ultraviolet light could make a zinc plate emit electrons, which he called “photoelectrons.”
Fast forward to 1905, a year famously known as Albert Einstein’s annus mirabilis, or “miracle year.” Among his several groundbreaking papers, Einstein proposed a radical idea: light could be thought of as being made up of particles, or “quanta,” which we now call photons. This was revolutionary because it challenged the classical wave theory of light.
Einstein suggested that when these photons hit the surface of a metal, they transfer their energy to electrons. If the photon’s energy is high enough, it can knock the electron out of the metal, causing the photoelectric effect. This was a pivotal moment in physics because it provided the first evidence of the quantum nature of light.
Einstein’s theory of the photoelectric effect was confirmed experimentally by Robert Millikan, despite his initial skepticism. For his work on the photoelectric effect, Einstein was awarded the Nobel Prize in Physics in 1921, not for his theory of relativity, as many would assume.
The photoelectric effect played a significant role in the development of quantum mechanics. It helped scientists understand that light and matter interact in quantized, or discrete, ways. This laid the foundation for modern physics and technology, influencing everything from the development of semiconductors to the exploration of quantum computing.
What is the Photoelectric Effect
Hertz’s Observations and the Photoelectric Effect:
In 1887, Heinrich Hertz was experimenting with electromagnetic waves when he made a serendipitous observation that would later become known as the photoelectric effect. Hertz was not trying to discover this effect; his primary goal was to prove the existence of electromagnetic waves predicted by James Clerk Maxwell’s equations.
During his experiments, Hertz noticed that when ultraviolet light shone upon the electrodes of a spark gap, sparks would jump between them more easily. This was a curious phenomenon because it suggested that the light was somehow affecting the electrical behavior of the gap.
Hertz’s observations were significant because they provided the first evidence that light could influence the emission of electrons from a material. However, at the time, Hertz did not realize the full implications of his discovery. It was not until later that scientists understood that what Hertz had observed was the emission of electrons due to the impact of light—a process now known as the photoelectric effect.
The photoelectric effect refers to the emission of electrons from a material when it is exposed to light. Hertz’s observations were the first step in understanding this effect, which would later be explained in detail by Albert Einstein.
Hertz’s work laid the groundwork for future research into the interaction between light and matter. His observations were crucial in the development of quantum mechanics and helped to establish the concept that light can behave as both a wave and a particle.
Hallwachs’ and Lenard’s Observations:
After Heinrich Hertz’s initial discovery, Wilhelm Hallwachs decided to investigate further. In 1888, he conducted an experiment where he exposed a zinc plate to ultraviolet light. He observed that the zinc plate, when illuminated, became positively charged, indicating that something was being emitted from the plate. Hallwachs concluded that the ultraviolet light was causing the zinc to lose electrons, which he called “photoelectrons.” This was one of the first clear demonstrations of the photoelectric effect.
Philipp Lenard, a student of Hertz, took these observations further. In the early 1900s, he conducted detailed experiments to study the photoelectric effect. Lenard used a variety of light sources and metals and measured the energy of the ejected electrons. He found that the energy of the photoelectrons was independent of the intensity of the light but depended on the light’s frequency. This was a puzzling result because, according to classical wave theory, the energy should have increased with the light’s intensity.
Lenard’s observations were crucial because they challenged the classical understanding of light and led to the development of quantum theory. His work showed that light must have particle-like properties, as the energy of the photoelectrons was related to the frequency of light, not its intensity. This was a key piece of evidence that supported Einstein’s later explanation of the photoelectric effect using the concept of photons.
For students, understanding Hallwachs’ and Lenard’s observations is important because it shows the scientific process in action—how careful experimentation and observation can lead to the revision of established theories. Their work helped to lay the foundation for quantum mechanics and changed our understanding of the nature of light and its interaction with matter.
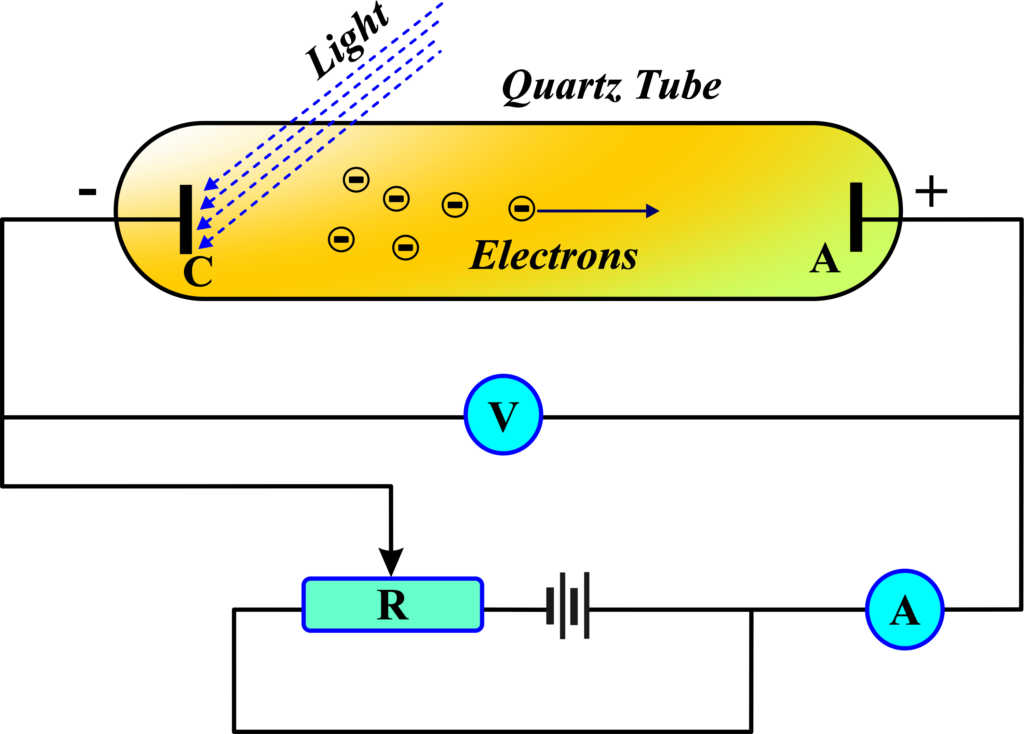
The photoelectric effect occurs when light or other electromagnetic radiation hits a material and causes it to emit electrons. These ejected electrons are called photoelectrons. Imagine you’re in a dark room with a metal plate and a flashlight. When you turn on the flashlight and direct the light toward the metal plate, something interesting happens: electrons start to leave the surface of the metal. This is the essence of the photoelectric effect.
In scientific terms, the photoelectric effect is the emission of electrons from a material when light shines on it. But not just any light will do; it has to be light that carries enough energy. These electrons that are ejected are known as photoelectrons.
Now, you might wonder, why does this happen? It’s because the light carries energy to the metal. When this energy is absorbed by the electrons, they get excited. If they get excited enough, they can escape from the attraction of the metal atoms and fly off into the space around the metal. This is similar to how a ball needs enough energy to roll out of a bowl.
The photoelectric effect is a clear demonstration of the particle nature of light. Each light particle, or photon, carries a specific amount of energy. When these photons hit the electrons, they transfer their energy to the electrons. If an electron receives enough energy from a photon, it can break free from the metal’s surface.
This phenomenon is not just a cool party trick for electrons; it’s a fundamental concept that helps us understand how light interacts with matter. It shows us that light has properties of both waves and particles, a duality that is central to quantum physics.
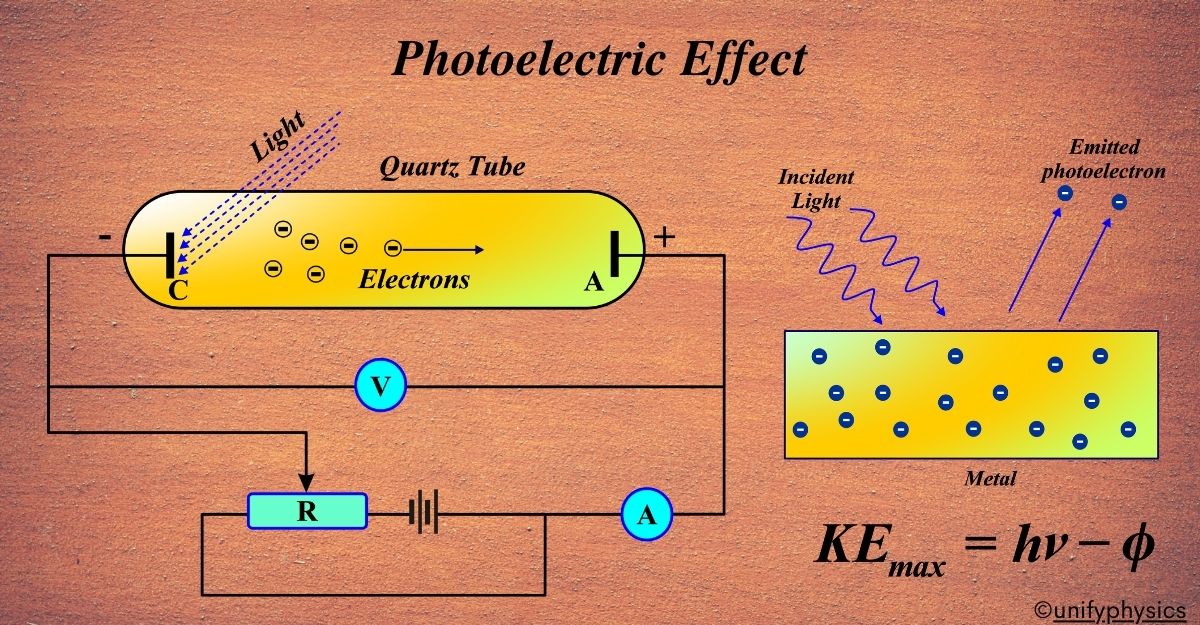
Experimental Study of the Photoelectric Effect
An experiment to study the photoelectric effect typically involves a few key components: A light source that can emit light of different frequencies and intensities. A photoelectric cell or tube that contains a metal surface (cathode) and a collector (anode). A power supply to apply a potential difference between the cathode and anode. An ammeter to measure the current produced by the ejected electrons.
The Procedure:
- Illuminating the Cathode: The metal surface is illuminated with light of a known frequency and intensity. If the frequency is above the threshold frequency for the metal, electrons are ejected.
- Measuring the Current: The ejected electrons move towards the anode, creating a current that can be measured by the ammeter. This current is the photoelectric current.
- Varying the Light: By changing the frequency and intensity of the light, students can observe how these factors affect the photoelectric current.
- Applying the Retarding Potential: A potential difference is applied to stop the most energetic electrons from reaching the anode. The minimum voltage required to stop the current is known as the stopping potential.
Observations: When the light’s frequency is increased (keeping the intensity constant), the stopping potential increases, indicating that the ejected electrons have more kinetic energy. When the light’s intensity is increased (keeping the frequency constant), the photoelectric current increases, but the stopping potential remains the same, indicating that more electrons are ejected, but their kinetic energy doesn’t change.
Analysis: The experiment confirms that the kinetic energy of the ejected electrons depends on the frequency of the light, not its intensity. The threshold frequency is determined by finding the frequency below which no current is observed regardless of the light’s intensity. The work function of the metal can be calculated using the stopping potential and the frequency of the light. The experiment demonstrates that light energy is quantized and that the energy of the ejected electrons is related to the frequency of the incident light.
Threshold Energy for the Photoelectric Effect
For the photoelectric effect to occur, the incoming photons must have energy greater than the material’s threshold energy, which is the minimum energy needed to remove an electron from the surface. To understand the threshold energy for the photoelectric effect, let’s imagine a locked door. This door represents the barrier that keeps electrons bound within a material. Now, to open this door and free the electrons, you need a key. In the world of physics, this key is the ‘threshold energy’.
Threshold energy is the minimum amount of energy that an electron needs to escape from the surface of a material. Think of it as the minimum ticket price for an electron to leave the ‘metal concert’ and venture out into the open space. If the energy of the incoming light (think of it as the currency of the photon world) is less than the ticket price, the electron cannot leave. It’s like showing up at a concert with not enough money to buy a ticket – you’re not getting in.
In the photoelectric effect, when light hits a material, each photon of that light carries a certain amount of energy. If the energy of the photon is equal to or greater than the threshold energy of the material, it can give an electron just the push it needs to break free from the material’s surface.
This threshold energy is unique to each material, much like different concerts have different ticket prices. For example, the threshold energy for metals like gold or silver is different from that for non-metal like selenium.
It’s important to note that the threshold energy is not about the number of photons, but about the energy each photon carries. So, even a dim light with few photons can cause the photoelectric effect if the photons have enough energy (if they’re part of high-energy light like ultraviolet). Conversely, a very bright light with lots of photons won’t cause the effect if the photons don’t have enough energy (like in the case of low-energy red light).
Imagine you’re at an amusement park, and there’s a ride with a height requirement. This height requirement is like the threshold energy—it’s the minimum you need to be able to go on the ride. In the photoelectric effect, electrons are like people wanting to go on a ride, and the photons (light particles) are like the measuring stick that shows if they’re tall enough (have enough energy).
The energy of a photon is given by the equation:
\(\displaystyle E = h\nu \)
Here, (E) is the energy of the photon, (h) is Planck’s constant, and (ν) is the frequency of the light.
There’s also a minimum frequency, called the threshold frequency (ν0), which is like the minimum height for the ride. Photons need to have at least this frequency to have enough energy to eject an electron.
The threshold energy (E0) is the energy corresponding to the threshold frequency. It’s calculated using the same formula as above, but with the threshold frequency:
\(\displaystyle E_0 = h\nu_0 \)
So, the threshold energy is the energy of a photon with the threshold frequency—the minimum energy needed for a photon to eject an electron from the material.
The expression for the threshold energy is derived from the energy of a photon, but it specifically uses the threshold frequency, which is the minimum frequency needed to start the photoelectric effect. Threshold energy is a fundamental concept in understanding the photoelectric effect. It’s the ‘price of admission’ for electrons to be ejected from a material, and it’s determined by the material’s unique properties and the energy of the incoming photons.
Relationship between Frequency and Kinetic Energy
The relationship between frequency and kinetic energy in the photoelectric effect is like the relationship between the color of light balls and the power they give to the targets in a video game. The higher the frequency of the light, the more energy it has, and the more kinetic energy the electrons will have when they’re knocked free.
Imagine you’re playing a video game where you have to hit targets with balls of light. Each ball of light has a different color, which represents a different frequency. Now, the targets are electrons that are stuck until they get hit by a ball of light with enough energy.
In this game, the frequency of the light ball (the color) determines how much energy it carries. The higher the frequency (like going from red to blue), the more energy the light ball has. When a light ball with a high enough frequency hits an electron target, it gives some of its energy to the electron. This energy is what allows the electron to break free and fly off the surface it was stuck to.
Now, let’s translate this into the physics of the photoelectric effect:
- Frequency: This is like the color of the light ball in the game. In real life, light comes in different frequencies, and each frequency corresponds to a different color of light. The frequency is important because it’s directly related to the energy of the light.
- Kinetic Energy: This is the energy that the electron has after it’s been hit by the light ball and breaks free. It’s like the speed and power the electron has as it flies away from the surface.
The relationship between the two is pretty straightforward: the higher the frequency of the light, the more kinetic energy the electron can have after it’s hit. This is because light with a higher frequency carries more energy, and it can transfer more of this energy to the electron.
Let’s derive the expression for the relationship between frequency and kinetic energy in the photoelectric effect. We’ll start with a simple analogy. Imagine you’re at a concert where the volume of the music can be adjusted. The volume is like the energy of the light, and the music is like the light itself. Now, the concert has a rule: you can only dance if the music is loud enough. This rule is like the threshold energy in the photoelectric effect—the minimum energy needed for electrons to be ejected from a material.
We know that the energy of a photon (a particle of light) is given by the equation:
\(\displaystyle E = h\nu \)
Here, (E) is the energy of the photon, (h) is Planck’s constant, and (ν) is the frequency of the light.
There’s a minimum frequency, called the threshold frequency (ν0), that’s needed to eject an electron. The energy of a photon at this frequency is the threshold energy (E0):
\(\displaystyle E_0 = h\nu_0 \)
When the frequency of the light is greater than the threshold frequency, the excess energy becomes the kinetic energy (KE) of the ejected electron:
\(\displaystyle KE = E – E_0 \)
Now, we substitute the expressions for (E) and (E0) into the equation for (KE):
\(\displaystyle KE = h\nu – h\nu_0 \)
Simplifying the equation, we get the expression for the kinetic energy of the ejected electron in terms of the frequency of the incident light:
\(\displaystyle KE = h(\nu – \nu_0) \)
So, the derived expression tells us that the kinetic energy of the ejected electron is proportional to the difference between the frequency of the incident light and the threshold frequency. It’s like saying the energy to dance (kinetic energy) depends on how much louder the music (frequency) is than the minimum volume needed to get you moving (threshold frequency). if you increase the frequency of the light (go from a low-energy color like red to a high-energy color like blue), you increase the kinetic energy of the electrons that are ejected. It’s like using a more powerful light ball in the game to hit the targets harder and make them fly off faster.
The expression (\(\displaystyle KE = h(\nu – \nu_0) \) shows the direct relationship between the frequency of the incident light and the kinetic energy of the emitted electrons, after accounting for the threshold frequency.
Principle of the Photoelectric Effect
The Minimum Condition for the Photoelectric Effect Explained:
When we talk about the photoelectric effect, there’s a basic rule that must be met for electrons to be ejected from a material’s surface: the light must have a certain minimum frequency. This is what we call the “minimum condition” for the photoelectric effect. For the photoelectric effect to occur, the incoming light can’t just be of any frequency. It has to be high enough to give the electrons enough energy to overcome the attraction of the metal. This minimum frequency is known as the threshold frequency.
The energy of a photon (a particle of light) is related to its frequency (ν) by the equation:
\(\displaystyle E = h \cdot \nu \)
where (E) is the energy of the photon and (h) is Planck’s constant. If the energy of the photon is less than the work function (Φ), which is the energy needed to eject an electron, then the photoelectric effect won’t happen.
So, the minimum condition for the photoelectric effect is that the frequency of the incident light must be equal to or greater than the threshold frequency. In formula terms, it’s:
\(\displaystyle \nu \geq \nu_0 \)
where (ν0) is the threshold frequency.
If the frequency of the light is below this threshold, no photoelectric effect will occur, regardless of the intensity of the light. This means you could shine a very bright red light (which has a low frequency) on a metal, and nothing would happen because the frequency isn’t high enough to meet the minimum condition.
The minimum condition for the photoelectric effect is like the minimum age requirement for a roller coaster ride. No matter how tall or eager you are, if you’re not old enough, you’re not getting on the ride. Similarly, if the light’s frequency isn’t high enough, electrons won’t be ejected, no matter how intense the light is.
Threshold Wavelength (λth):
To understand the concept of threshold wavelength for the photoelectric effect, let’s consider a simple analogy. Imagine you’re at a theme park, and there’s a ride with a height marker at the entrance. Just like you need to be tall enough to go on the ride, electrons need light of a certain wavelength—or shorter—to be ejected from a material’s surface.
The threshold wavelength is the maximum wavelength of light that can cause electrons to be ejected from a material. It’s like the maximum height limit for the ride; if you’re taller (or in the case of light, if the wavelength is shorter), you can get on the ride (or eject an electron).
In the photoelectric effect, light is made up of particles called photons, and each photon carries energy. The energy of a photon is inversely related to its wavelength, which means shorter wavelengths have more energy.
The relationship between the energy of a photon and its wavelength is given by:
\(\displaystyle E = \frac{hc}{\lambda} \)
- (E) is the energy of the photon,
- (h) is Planck’s constant,
- (c) is the speed of light,
- (λ) is the wavelength of the photon.
For the photoelectric effect to occur, the energy of the photon must be greater than the work function (Φ) of the material. The threshold wavelength is the longest wavelength (or the least energy) that can still provide enough energy to overcome the work function. It’s calculated by:
\(\displaystyle \lambda_{th} = \frac{hc}{\Phi} \)
If the wavelength of the incident light is longer than the threshold wavelength, the photons don’t have enough energy to eject electrons, no matter how intense the light is. This is why ultraviolet light can cause the photoelectric effect in many materials, while visible light often cannot.
The threshold wavelength sets the limit for the longest wavelength of light that can still have enough energy to eject electrons from a material.
Work Function or Threshold Energy (Φ):
When we discuss the photoelectric effect, the term “work function” or “threshold energy” (Φ) comes up frequently. It’s a crucial concept that students need to understand clearly. The work function is the minimum energy required to remove an electron from the surface of a material. You can think of it as the ‘energy ticket’ that an electron needs to get out of the metal ‘concert hall’. If the electron doesn’t have this ‘ticket’, it can’t leave, no matter how much light you shine on it.
The work function is a property of the material itself. Different materials hold onto their electrons with varying strengths, which means they have different work functions. Metals, for example, have a lower work function compared to non-metals.
The work function is usually given in electron volts (eV) and can be calculated using the equation:
\(\displaystyle\Phi = h \cdot \nu_0 \)
- (Φ) is the work function,
- (h) is Planck’s constant (\(\displaystyle 6.626 \times 10^{-34} ) Js\)),
- (ν0) is the threshold frequency, the minimum frequency needed to eject an electron.
In the context of the photoelectric effect, when light of a certain frequency (ν) hits the material, each photon carries energy. If the photon’s energy is equal to or greater than the work function (Φ), it can give an electron enough energy to escape the material’s surface.
The work function is like a gatekeeper for the electrons. It determines whether the incoming light has enough energy to ‘pay’ for the electrons’ release. If the energy of the light (which depends on its frequency) is less than the work function, the gate remains closed, and no electrons are ejected.
The work function or threshold energy (Φ) is a fundamental concept in the photoelectric effect. It’s the energy barrier that electrons must overcome to be ejected from a material when it is exposed to light.
Equation of Photoelectric Effect
Einstein’s photoelectric equation is a cornerstone of modern physics that explains several key concepts related to the photoelectric effect. The equation starts with the idea that light is made up of particles called photons, each carrying a discrete amount of energy. This energy is directly related to the frequency of the light. The higher the frequency, the more energy each photon has.
Einstein’s equation supports the quantum theory, which says that light has both wave-like and particle-like properties. This was a revolutionary concept at the time because it challenged the classical wave theory of light. The equation explains how photons can transfer their energy to electrons in a material, causing those electrons to be ejected. This is the actual “photoelectric effect.”
It introduces the concept of a threshold frequency, which is the minimum frequency of light required to eject an electron from a material. If the light’s frequency is below this threshold, no electrons will be emitted, regardless of the light’s intensity. The equation describes how the kinetic energy of the emitted electrons depends on the frequency of the incident light. It shows that the kinetic energy is proportional to the frequency, minus the threshold frequency.
The formula for Einstein’s photoelectric equation is:
\(\displaystyle KE = h\nu – \Phi \)
Here, (KE) is the kinetic energy of the emitted electron, (h) is Planck’s constant, (\nu) is the frequency of the incident light, and (Φ) is the work function of the material (the energy needed to remove an electron).
The equation tells us that the kinetic energy of the ejected electron is the difference between the energy of the incoming photon and the work function of the material. If the photon’s energy is just equal to the work function, the electron will be ejected with zero kinetic energy—it will just barely get out. If the photon’s energy is higher, the excess energy becomes the kinetic energy of the ejected electron.
Characteristics of the Photoelectric Effect
The photoelectric effect is not just a simple emission of electrons due to light; it has specific characteristics that define its behavior. Understanding these characteristics is crucial for students to grasp the concept fully. Here are the main features:
Instantaneous Response: One of the most striking characteristics of the photoelectric effect is that the emission of electrons occurs almost instantaneously as soon as the light hits the material’s surface. There is no noticeable delay between the absorption of light and the release of electrons.
Effect of Light Intensity: The number of electrons emitted in the photoelectric effect is directly proportional to the intensity of the incident light. More intense light means more photons hitting the surface, which results in more electrons being ejected.
Effect of Light Frequency: The kinetic energy of the emitted electrons is independent of the light’s intensity but depends on the frequency of the light. Higher frequency light (which has more energy per photon) will result in electrons with greater kinetic energy.
Threshold Frequency: There is a minimum frequency of light below which no electrons are emitted, regardless of the intensity of the light. This minimum frequency is called the threshold frequency, and it is specific to the material being illuminated.
Energy Transfer: The energy transfer from the light to the electrons is quantized. Each photon can eject only one electron, transferring a discrete packet of energy to the electron.
Material Dependency: Different materials have different work functions, which means the threshold frequency and the kinetic energy of the emitted electrons will vary from one material to another.
If the frequency of the incident light is below the threshold frequency, increasing the light intensity will not cause the photoelectric effect. The electrons simply do not have enough energy to overcome the material’s work function.
Einstein’s Contributions
Albert Einstein’s contribution to the photoelectric effect is one of the most significant milestones in the development of modern physics. To explain this to 12th-grade students, let’s simplify the concept. Before Einstein, scientists observed the photoelectric effect but couldn’t explain why light could eject electrons from a material only if it had a frequency higher than a certain threshold, regardless of its intensity.
In 1905, Einstein proposed a groundbreaking hypothesis: light is made up of particles called photons. Each photon carries a quantum of energy that depends on the light’s frequency. This was a bold step because it challenged the prevailing wave theory of light.
Einstein suggested that when a photon hits an electron, it transfers its energy to the electron. If this energy is greater than the material’s work function (the energy needed to eject an electron), the electron is emitted with kinetic energy. He gave us the equation:
\(\displaystyle KE = h \cdot \nu – \Phi \)
Einstein’s explanation of the photoelectric effect earned him the Nobel Prize in Physics in 1921. His work was crucial because it provided strong evidence for the quantum theory of light, which was a radical departure from classical physics.
Einstein’s contribution to the photoelectric effect laid the foundation for quantum mechanics. It changed our understanding of light and matter, showing that light has both wave-like and particle-like properties.
Also Read: Electron Emission
Factors Affecting the Photoelectric Effect
The main factors are the intensity of the incident light, the frequency of the incident light, and the type of material being hit by the photons.
Type of Material: Different materials have different work functions, which is the minimum energy needed to eject an electron. Metals with a low work function are more sensitive to the photoelectric effect.
Frequency of Incident Light: The frequency of the light must be above a certain threshold for the photoelectric effect to occur. Light with a frequency below this threshold, no matter how intense, will not cause electrons to be ejected.
Intensity of Incident Light: While the frequency of the light determines if electrons can be ejected, the intensity of the light affects how many electrons are ejected. Higher intensity means more photons hitting the surface per second, leading to more ejected electrons.
Surface Condition: The cleanliness and smoothness of the material’s surface can influence the photoelectric effect. A clean, smooth surface can emit electrons more easily than a dirty or oxidized one.
Temperature of the Material: Higher temperatures can increase the energy of the electrons within the material, making it easier for them to be ejected when light is shone upon the surface.
Light Polarization: Polarized light can affect the photoelectric effect because it can interact with electrons in specific directions, depending on the material’s structure.
These factors collectively determine how readily a material will exhibit the photoelectric effect when exposed to light.
Different Graphs of the Photoelectric Equation
Graphs are a powerful tool for visualizing the relationships described by the photoelectric effect. Let’s explore the different types of graphs that illustrate the photoelectric equation and what they tell us.
(i) Photoelectric Current vs Retarding Potential for Different Voltages

This graph illustrates how the photoelectric current changes with varying retarding potentials applied to stop the ejected electrons. For different voltages of incident light, the graph shows a decrease in current as the retarding potential increases, until it reaches zero.
The point where the current becomes zero is the stopping potential, which is crucial for determining the maximum kinetic energy of the ejected electrons.
(ii) Photoelectric Current vs Retarding Potential for Different Intensities
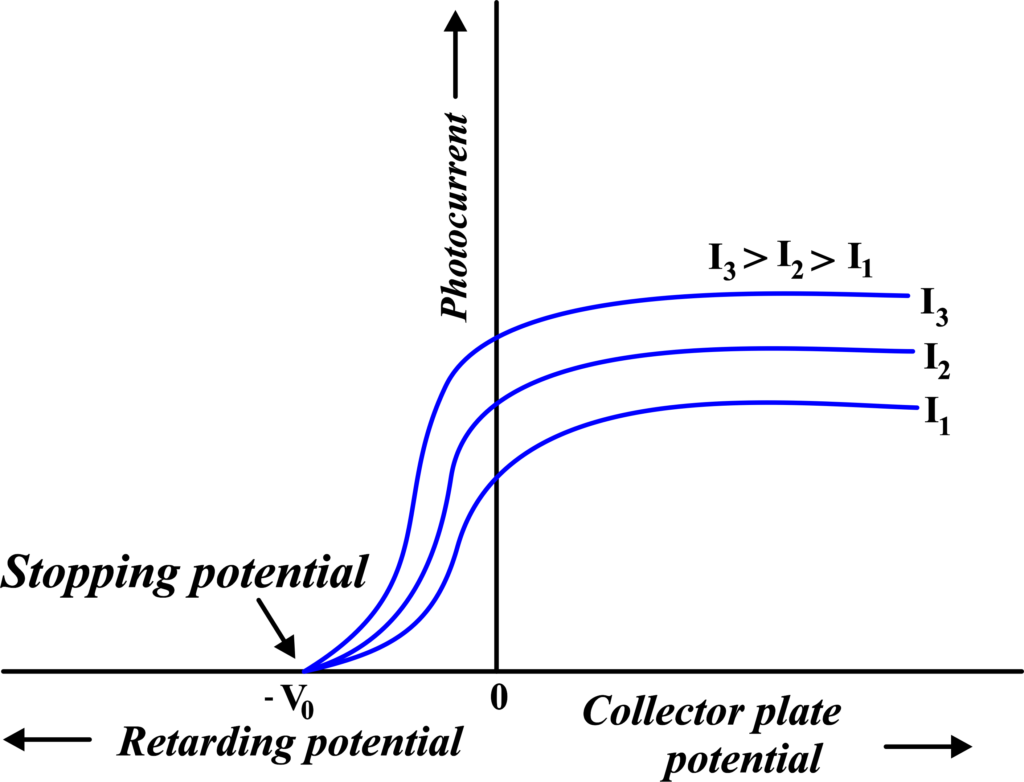
Similar to the first graph, this one compares the photoelectric current against the retarding potential, but for different intensities of incident light. Higher intensities result in a higher maximum current, indicating more electrons are being ejected.
However, the stopping potential remains unchanged, showing that intensity doesn’t affect the kinetic energy of the ejected electrons.
(iii) Electron Current vs Light Intensity
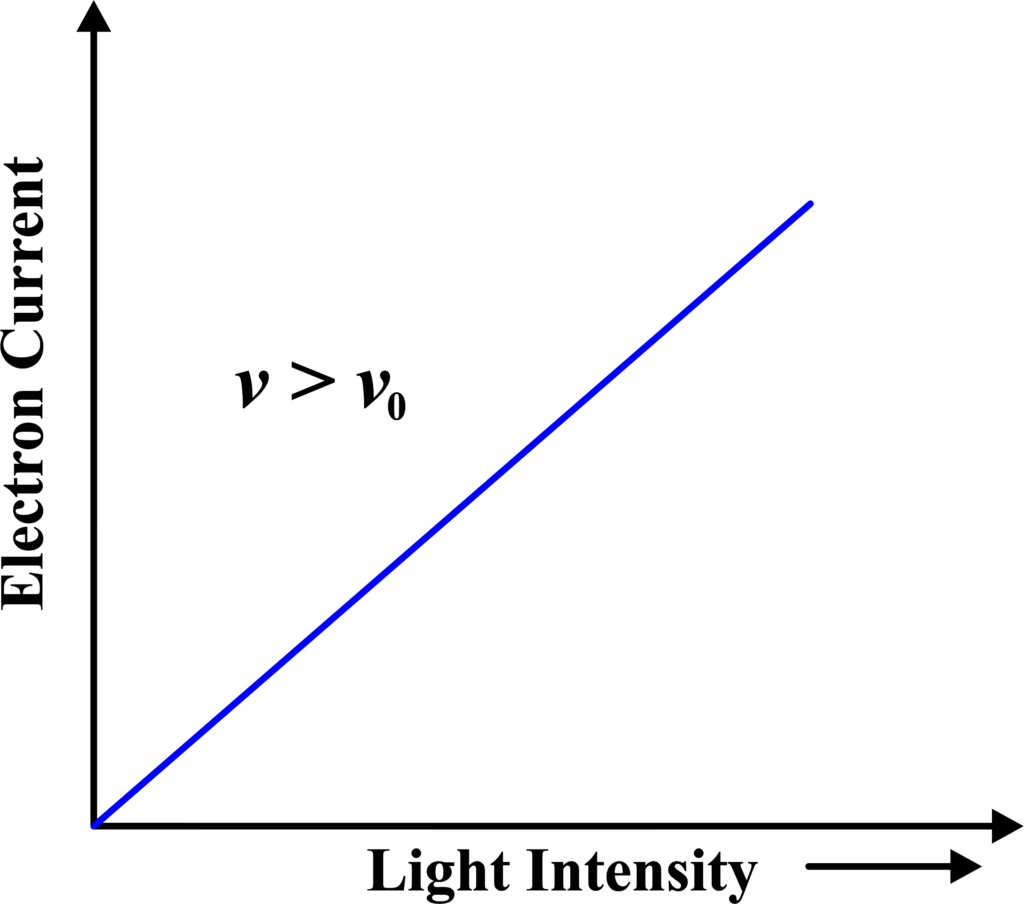
This graph plots the electron current (proportional to the number of ejected electrons) against the intensity of the incident light. It typically shows a linear relationship, confirming that the number of electrons ejected increases with the light’s intensity, provided the frequency is above the threshold.
(iv) Stopping Potential vs Frequency
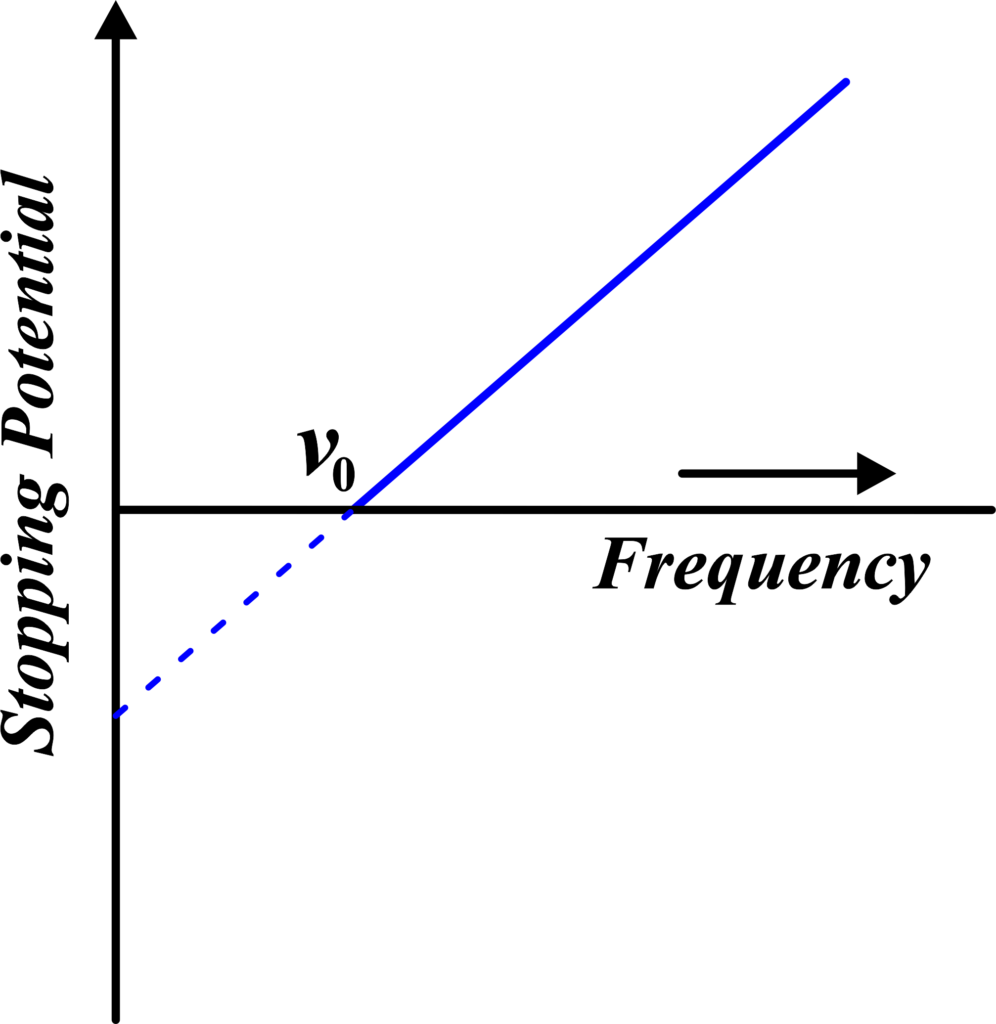
Here, the stopping potential needed to stop the ejected electrons is plotted against the frequency of the incident light. The graph is a straight line, indicating a linear relationship. The slope of this line is related to Planck’s constant, and the intercept on the frequency axis gives the threshold frequency, which is a fundamental property of the material.
(v) Electron Current vs Light Frequency

This graph shows the electron current as a function of the light frequency. Below the threshold frequency, the current is zero, and it begins to increase as the frequency surpasses this threshold. This graph demonstrates the existence of a threshold frequency and the quantized nature of energy transfer in the photoelectric effect.
(vi) Electron Kinetic Energy vs Light Frequency

This graph plots the kinetic energy of the ejected electrons against the frequency of the incident light. It’s a straight line with a positive slope, starting from the threshold frequency. The slope gives Planck’s constant, and the graph illustrates the direct proportionality between the photoelectrons’ kinetic energy and the incident light’s frequency, once above the threshold frequency.
These graphs provide a visual representation of the principles governing the emission of electrons due to incident light, illustrating the linear relationships and thresholds that are central to this quantum phenomenon.
Applications of the Photoelectric Effect
The photoelectric effect is not just a theoretical concept; it has many practical applications that have become integral to our daily lives. Here’s how this quantum phenomenon is put to use:
- Solar Panels
One of the most well-known applications of the photoelectric effect is in solar panels. These panels contain cells that convert sunlight directly into electricity using the photoelectric effect, providing a renewable energy source. - Photocells
Photocells, or photoelectric cells, use the photoelectric effect to detect light. They are used in automatic lighting systems, like street lights that turn on at dusk, and in security systems that detect when a beam of light is interrupted. - Digital Cameras
The sensors in digital cameras use the photoelectric effect to convert the light that hits them into electrical signals, which are then processed to create digital images. - Light Meters
Photographers use light meters to measure the intensity of light. These devices rely on the photoelectric effect to provide readings that help photographers set the correct exposure for their pictures. - Space Telescopes
Space telescopes, like the Hubble Space Telescope, use sensors that operate on the principle of the photoelectric effect to detect light from distant stars and galaxies, helping astronomers explore the universe. - Smoke Detectors
Some types of smoke detectors use a small photocell to detect smoke particles. When smoke interrupts the light beam, the change in the photocell’s current triggers the alarm. - Laboratory Equipment
In scientific research, equipment like spectrophotometers uses the photoelectric effect to measure the properties of light absorption and emission by materials, aiding in chemical analysis and other studies.
Solved Examples
Problem 1: Monochromatic light of wavelength (400nm) is incident on a metal surface with a work function of (2.2 eV). Calculate the stopping potential required to stop the emitted photoelectrons.
Solution: First, calculate the energy of the incident photons using (\(\displaystyle E = \frac{hc}{\lambda} \)).
\(\displaystyle E = \frac{6.63 \times 10^{-34} \times 3 \times 10^8}{400 \times 10^{-9}} = \frac{1.989 \times 10^{-25}}{400 \times 10^{-9}} \)
\(\displaystyle = 4.97 \times 10^{-19} \, \text{J}\)
Convert the energy to electron volts:
\(\displaystyle E = \frac{4.97 \times 10^{-19}}{1.6 \times 10^{-19}} = 3.1 \, \text{eV}\)
Using the photoelectric equation (\(\displaystyle E = \phi + K_{\text{max}} \)):
\(\displaystyle 3.1 \, \text{eV} = 2.2 \, \text{eV} + K_{\text{max}}\)
\(\displaystyle K_{\text{max}} = 3.1 \, \text{eV} – 2.2 \, \text{eV} = 0.9 \, \text{eV}\)
The stopping potential (Vs) is given by the kinetic energy of the emitted electrons:
\(\displaystyle eV_s = K_{\text{max}}\)
\(\displaystyle V_s = \frac{K_{\text{max}}}{e} = 0.9 \, \text{V}\)
The stopping potential required to stop the emitted photoelectrons is (0.9 V).
Problem 2: A certain metal has a work function of ( 3.0 eV). Calculate the threshold wavelength for photoelectric emission.
Solution: The threshold wavelength (\lambda_th) can be found using the equation (\(\displaystyle \phi = \frac{hc}{\lambda_{\text{th}}} \)).
Convert the work function to joules:
\(\displaystyle\phi = 3.0 \times 1.6 \times 10^{-19} \, \text{J} = 4.8 \times 10^{-19} \, \text{J}\)
\(\displaystyle\lambda_{\text{th}} = \frac{hc}{\phi} = \frac{6.63 \times 10^{-34} \times 3 \times 10^8}{4.8 \times 10^{-19}}\)
\(\displaystyle\lambda_{\text{th}} = \frac{1.989 \times 10^{-25}}{4.8 \times 10^{-19}} = 414.38 \times 10^{-9} \, \text{m}\)
\(\displaystyle = 414.38 \, \text{nm}\)
The threshold wavelength for photoelectric emission is (414.38 nm).
Problem 3: Light of frequency (\(\displaystyle 8 \times 10^{14} \, \text{Hz} \)) is incident on a metal surface with a work function of (2.5 eV). Calculate the maximum kinetic energy of the emitted photoelectrons.
Solution: First, calculate the energy of the incident photons using ( E = hν):
\(\displaystyle E = 6.63 \times 10^{-34} \times 8 \times 10^{14} = 5.304 \times 10^{-19} \, \text{J}\)
Convert the energy to electron volts:
\(\displaystyle E = \frac{5.304 \times 10^{-19}}{1.6 \times 10^{-19}} = 3.315 \, \text{eV}\)
Using the photoelectric equation ( \(\displaystyle E = \phi + K_{\text{max}} \)):
\(\displaystyle 3.315 \, \text{eV} = 2.5 \, \text{eV} + K_{\text{max}}\)
\(\displaystyle K_{\text{max}} = 3.315 \, \text{eV} – 2.5 \, \text{eV} = 0.815 \, \text{eV}\)
The maximum kinetic energy of the emitted photoelectrons is (0.815 eV).
Problem 4: A metal surface with a work function of (4.0eV) is illuminated with light of wavelength (250 nm). Determine if photoelectric emission will occur and, if so, find the maximum kinetic energy of the emitted electrons.
Solution: First, calculate the energy of the incident photons using (\(\displaystyle E = \frac{hc}{\lambda} \)):
\(\displaystyle E = \frac{6.63 \times 10^{-34} \times 3 \times 10^8}{250 \times 10^{-9}} = \frac{1.989 \times 10^{-25}}{250 \times 10^{-9}}\)
\(\displaystyle = 7.956 \times 10^{-19} \, \text{J}\)
Convert the energy to electron volts:
\(\displaystyle E = \frac{7.956 \times 10^{-19}}{1.6 \times 10^{-19}} = 4.9725 \, \text{eV}\)
Since the photon energy (4.9725 eV) is greater than the work function (4.0 eV), photoelectric emission will occur. The maximum kinetic energy (Kmax) of the emitted electrons is given by:
\(\displaystyle K_{\text{max}} = E – \text{work function} = 4.9725 \, \text{eV} – 4.0 \, \text{eV} = 0.9725 \, \text{eV}\)
Photoelectric emission will occur, and the maximum kinetic energy of the emitted electrons is (0.9725 eV).
Problem 5: Determine the minimum frequency of light required to cause photoelectric emission from a metal with a work function of (3.2 eV).
Solution: The minimum frequency (νmin) required can be found using the equation (Φ = hνmin).
Convert the work function to joules:
\(\displaystyle\phi = 3.2 \times 1.6 \times 10^{-19} \, \text{J} = 5.12 \times 10^{-19} \, \text{J}\)
\(\displaystyle\nu_{\text{min}} = \frac{\phi}{h} = \frac{5.12 \times 10^{-19}}{6.63 \times 10^{-34}} = 7.72 \times 10^{14} \, \text{Hz}\)
The minimum frequency of light required to cause photoelectric emission from the metal is (\(\displaystyle 7.72 \times 10^{14} \, \text{Hz} \)).
Problem 6: If the stopping potential for a photoelectric experiment is (3.0 V) and the wavelength of incident light is (400 nm), determine the work function of the metal.
Solution: First, calculate the energy of the incident photons using ( \(\displaystyle E = \frac{hc}{\lambda} \)):
\(\displaystyle E = \frac{6.63 \times 10^{-34} \times 3 \times 10^8}{400 \times 10^{-9}} = \frac{1.989 \times 10^{-25}}{400 \times 10^{-9}}\)
\(\displaystyle = 4.97 \times 10^{-19} \, \text{J}\)
Convert the energy to electron volts:
\(\displaystyle E = \frac{4.97 \times 10^{-19}}{1.6 \times 10^{-19}} = 3.1 \, \text{eV}\)
The stopping potential (Vs) is given as (3.0 V), which means the kinetic energy (K_max) of the emitted electrons is:
\(\displaystyle K_{\text{max}} = eV_s = 3.0 \, \text{eV}\)
Using the photoelectric equation ( \(\displaystyle E = \phi + K_{\text{max}} \)):
\(\displaystyle 3.1 \, \text{eV} = \phi + 3.0 \, \text{eV}\)
\(\displaystyle \phi = 3\)
\(\displaystyle1 \, \text{eV} – 3.0 \, \text{eV} = 0.1 \, \text{eV}\)
The work function of the metal is 0.1eV
Q: Can you explain why red light doesn’t cause the photoelectric effect?
Answer: Each material has a characteristic work function (Φ), which is the minimum energy needed to eject an electron from the material’s surface. This energy is specific to the material and is a measure of how strongly the material holds onto its electrons.
The energy of light is related to its frequency (ν) by the equation:
\(\displaystyle E = h \cdot \nu \)
Since red light has a lower frequency compared to other colors like blue or ultraviolet, it also has less energy per photon.
For the photoelectric effect to occur, the energy of the incoming photons must be equal to or greater than the work function of the material. If the photon’s energy is less than the work function, it won’t be able to eject electrons.
Red light has a lower frequency and therefore lower energy photons compared to blue or ultraviolet light. If the energy of red light photons is less than the work function of the material, they won’t have enough energy to eject electrons, and thus, no photoelectric effect will be observed.
Red light doesn’t cause the photoelectric effect on a material if its photons don’t carry enough energy to overcome the binding energy (work function) of the electrons in the material. It’s all about matching or exceeding that energy threshold to free the electrons and observe the photoelectric effect.
FAQs
What is the photoelectric effect and why is it significant in physics?
The photoelectric effect is the phenomenon where electrons are emitted from the surface of a material, usually a metal, when it is exposed to light of sufficient frequency. This effect is significant because it provided evidence for the particle nature of light and supported the concept of photons, which played a crucial role in the development of quantum mechanics.
What is the threshold energy for the photoelectric effect?
The threshold energy, also known as the work function, is the minimum energy required to eject an electron from the surface of a material. It is specific to each material and represents the energy needed to overcome the attraction between the electron and the atomic nucleus. Only photons with energy equal to or greater than the work function can cause photoemission.
How is the frequency of incident light related to the kinetic energy of emitted electrons in the photoelectric effect?
The kinetic energy of the emitted electrons is directly related to the frequency of the incident light. When light with a frequency higher than the threshold frequency strikes a material, the excess energy (above the work function) is converted into the kinetic energy of the emitted electrons. Higher frequency light results in greater kinetic energy of the ejected electrons.
What is the equation of the photoelectric effect?
The equation of the photoelectric effect, formulated by Einstein, describes the relationship between the energy of the incident photons, the work function of the material, and the kinetic energy of the emitted electrons. It states that the energy of the incident photon is equal to the sum of the work function and the kinetic energy of the emitted electron.
What were Einstein’s contributions to the understanding of the photoelectric effect?
Einstein’s major contribution was his explanation of the photoelectric effect using the concept of light quanta, or photons. He proposed that light consists of discrete packets of energy and that the energy of each photon is proportional to its frequency. This explanation provided a theoretical basis for the observed experimental results and earned him the Nobel Prize in Physics in 1921.
What is the minimum condition for the photoelectric effect to occur?
The minimum condition for the photoelectric effect to occur is that the frequency of the incident light must be equal to or greater than the threshold frequency of the material. The threshold frequency is the minimum frequency required for the photons to have enough energy to overcome the work function and eject electrons from the material’s surface.
What is the threshold wavelength (λth) and how is it related to the work function?
The threshold wavelength (λth) is the maximum wavelength of light that can cause the photoelectric effect for a given material. It is inversely related to the threshold frequency, and thus to the work function, of the material. Light with a wavelength longer than the threshold wavelength does not have enough energy to overcome the work function and eject electrons.