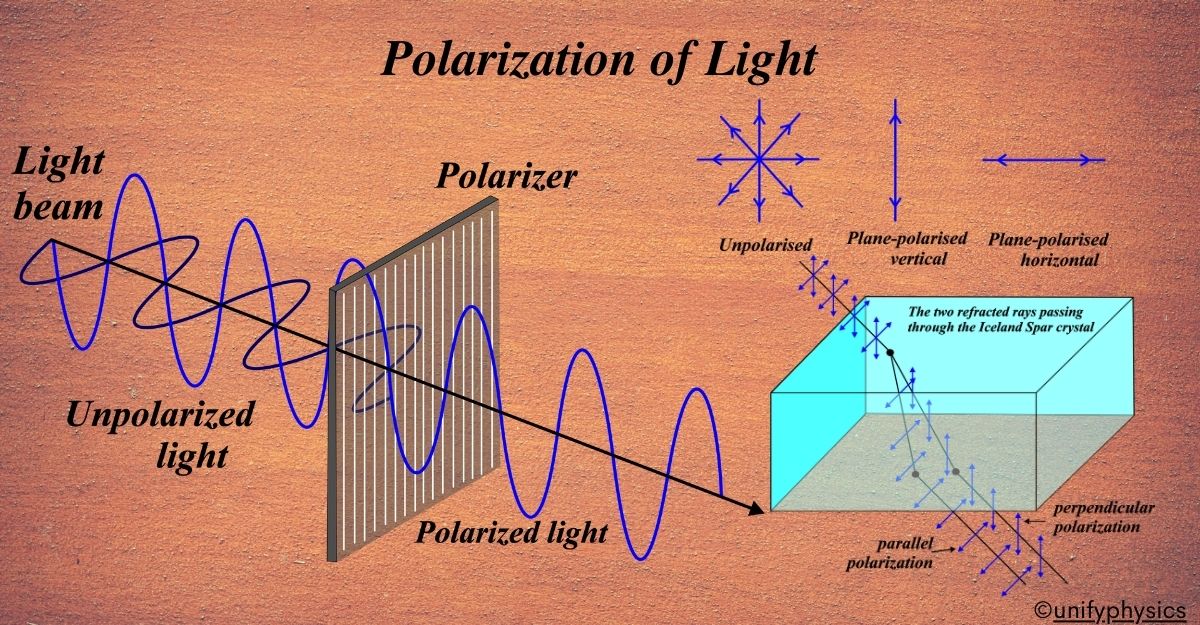
The story of light polarization is quite fascinating and begins in the 17th century. It was a time of great scientific discovery and one of the mysteries that puzzled scientists was the nature of light.
Erasmus Bartholinus, a Danish scientist, made a groundbreaking discovery in 1669. He was studying a naturally occurring crystal called Iceland spar. When he looked through this crystal, he noticed something peculiar: objects appeared double. This phenomenon, known as double refraction, suggested that light could behave in a way that was not yet understood.
This observation laid the groundwork for the concept of polarization. However, it wasn’t until the early 19th century that the term “polarization” was coined. The French physicist Étienne-Louis Malus in 1808 discovered that when light reflects off a surface, its waves could be oriented in a particular direction. He observed this by looking at the light reflected from the windows of the Luxembourg Palace in Paris through a crystal, noticing changes in brightness as he rotated the crystal. This directional property of light waves was what he called “polarization.”
The understanding of light as a wave was further developed by other scientists like Augustin-Jean Fresnel and Thomas Young. They showed that light waves, unlike sound waves, were transverse, meaning they oscillated perpendicular to the direction of travel. This was a key insight into understanding polarization.
In the mid-19th century, James Clerk Maxwell revolutionized the field with his theory of electromagnetism, which described light as an electromagnetic wave. His equations predicted that light waves were transverse and could indeed be polarized.
What is the Polarization of Light?
Polarization of light refers to the orientation of the light’s electric field. Normally, light vibrates in all directions perpendicular to its direction of travel. When light is polarized, its electric field oscillates in a single plane.
Imagine light as a wave, similar to waves on the surface of a pond. Now, light waves are special because they can move in different directions at the same time. This is because light is a transverse wave, which means it vibrates in directions that are perpendicular to the direction it’s traveling.
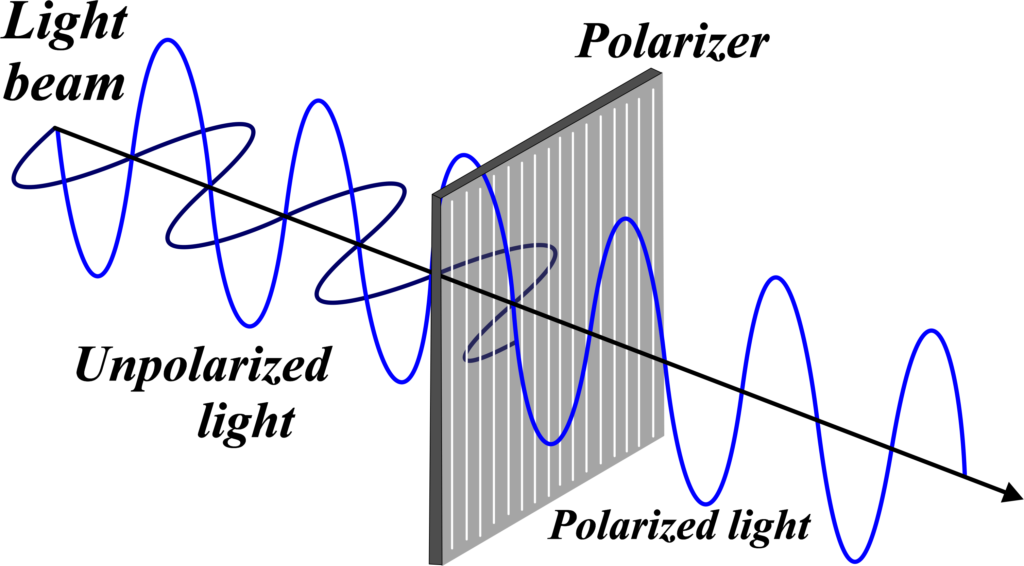
When light is emitted from a source, like the sun or a lamp, it vibrates in all possible directions perpendicular to its path. This is known as unpolarized light because there’s no specific direction to these vibrations.
Now, polarization is like taking this jumble of vibrations and making them orderly. When light is polarized, all its waves vibrate in the same direction or plane. It’s as if you’ve taken a comb and neatly aligned all the waves in one direction. This is polarized light.
To visualize this, think of a jump rope. If you shake the rope up and down, you create a wave that moves horizontally but vibrates vertically. That’s similar to how polarized light works, except light waves are much smaller and faster.
Polarization of light is about aligning the chaotic, multi-directional vibrations of light into a single, well-ordered direction. It’s a fundamental property of light that has profound implications in physics, technology, and even nature. For example, polarized sunglasses work by blocking certain directions of light waves, reducing glare.
Transverse Waves and Longitudinal Waves
Transverse Waves:
Transverse waves are all about the direction of motion being perpendicular to the direction of travel. Examples include light waves and ripples in water. To understand transverse waves, let’s start with something familiar: a wave on a string. Imagine you’re holding a rope and you flick your wrist up and down. The wave that travels along the rope moves horizontally, but the actual motion of the rope is up and down. This is the essence of a transverse wave.
In transverse waves, the displacement of the medium (in our case, the rope) is perpendicular to the direction of the wave’s travel. If the wave is moving to the right, the medium moves up and down or side to side.
Now, let’s relate this to light. Light waves are also transverse waves, but instead of the up-and-down motion of a rope, light waves have electric and magnetic fields oscillating perpendicular to the direction of the wave’s travel. These fields are what make up electromagnetic waves, which is what light is.
Here’s a simple way to picture it:
- Electric Field: Imagine it as the up-and-down motion of the rope.
- Magnetic Field: Think of it as a side-to-side motion that’s at a right angle to the electric field.
Both these fields travel together through space, and this combination of electric and magnetic oscillations is what allows light to be polarized, which means aligning these oscillations in a particular direction.
It’s a fundamental concept that helps us understand not just ropes and ripples, but also the very nature of light and other electromagnetic waves. It’s like dancers in a line dance moving side to side while the line progresses forward; each dancer’s movement is a transverse wave in action.
Longitudinal Waves:
The oscillations are parallel to the direction of the wave’s travel. Sound waves are a common example. Imagine you have a slinky in front of you. If you push and pull one end of the slinky back and forth, you’ll create a series of compressions and rarefactions that move along the length of the slinky. This is a longitudinal wave.
In longitudinal waves, the particles of the medium move parallel to the direction of the wave’s travel. The areas where the particles are close together are called compressions, and the areas where they are spread apart are called rarefactions.
Now, let’s relate this to sound, which is a common example of a longitudinal wave. When a drum is hit, it vibrates back and forth. These vibrations push on the air molecules around the drum, creating compressions and rarefactions that travel through the air to your ears. That’s how you hear sound.
Unlike transverse waves, where the motion is perpendicular, longitudinal waves, are all about the back-and-forth motion in the same direction as the wave is moving. It’s like a traffic jam where cars bunch up (compression) and then spread out (rarefaction) as they move along the road.
So, longitudinal waves are characterized by the parallel motion of particles with respect to the wave’s direction. Understanding this concept is crucial for grasping how sounds travel through different mediums and is a fundamental aspect of wave physics. It’s the push and pull, the squeeze and stretch that makes these waves an essential part of our world, from the music we enjoy to the voices we hear.
Types of Polarization of Light
There are three main types of polarization:
Linear Polarization:
When we talk about the polarization of light, we’re referring to the direction in which the electric field of the light wave oscillates. Linear polarization is one of the simplest forms of polarization, and it’s quite easy to visualize.
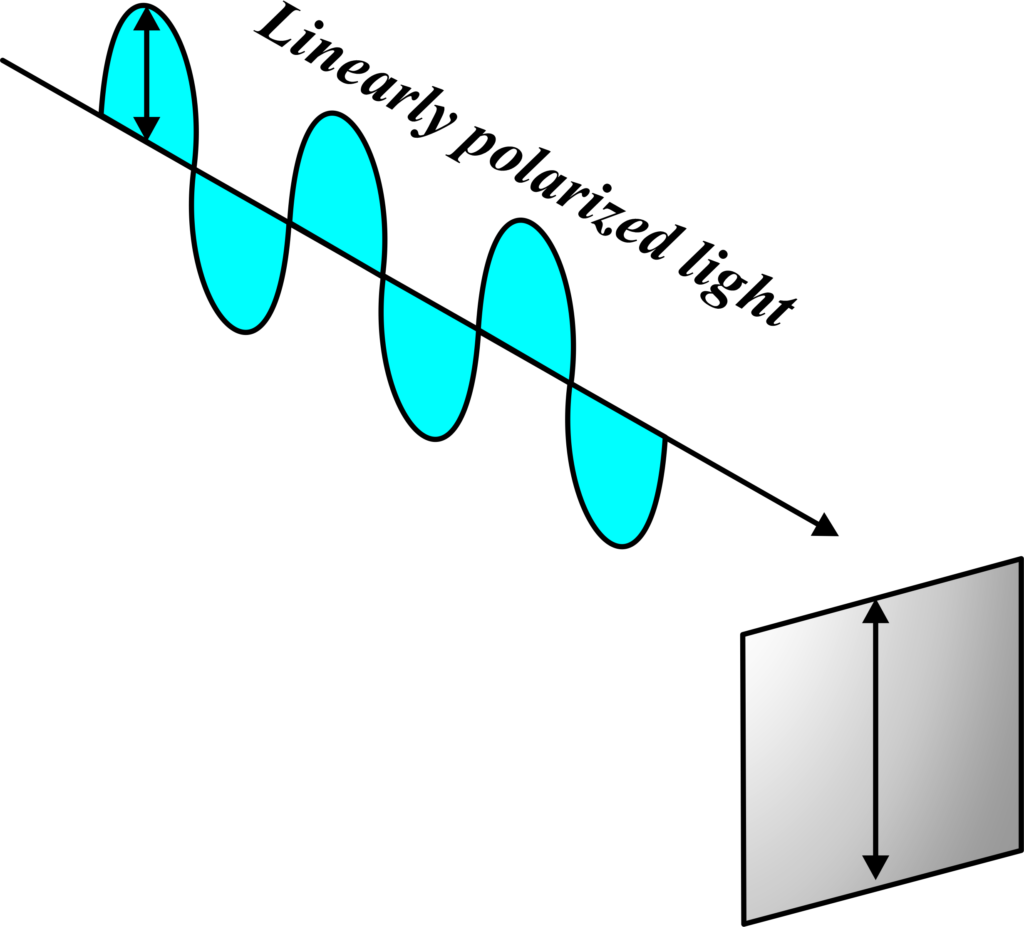
Imagine light as a wave moving towards you, like a wave in the ocean. Now, if this wave could only move up and down as it approaches you, it would be similar to linearly polarized light. In linear polarization, the electric field of the light wave oscillates in a single plane or direction. It’s as if the light wave is confined to move within invisible walls that only allow it to go up and down, not side to side.
Here’s a simple analogy: think of a group of people jumping on a trampoline. If everyone is jumping up and down in sync, their motion represents a linearly polarized wave. They are all moving in the same direction at the same time, just like the electric field in linearly polarized light.
In technical terms, if the light is traveling in the z-direction, the electric field may be oscillating back and forth in the x-direction. This would be represented mathematically as:
\(\displaystyle E(z,t) = E_0 \cos(kz – \omega t) \)
where (E(z,t)) is the electric field at position (z) and time (t), (E0) is the maximum amplitude of the wave, (k) is the wave number, and (ω) is the angular frequency.
So, linear polarization is when the light wave’s electric field vibrates in one direction or plane. It’s a neat and orderly form of light that’s used in many applications, from the screens we watch to the scientific instruments that help us understand the universe. It’s like a disciplined march of waves, all moving in unison in a single direction.
Circular Polarization:
Circular polarization is a fascinating concept where the light wave’s electric field rotates in a circular motion as the wave travels forward. It’s like a spiral staircase of light, with the steps representing the electric field’s path.
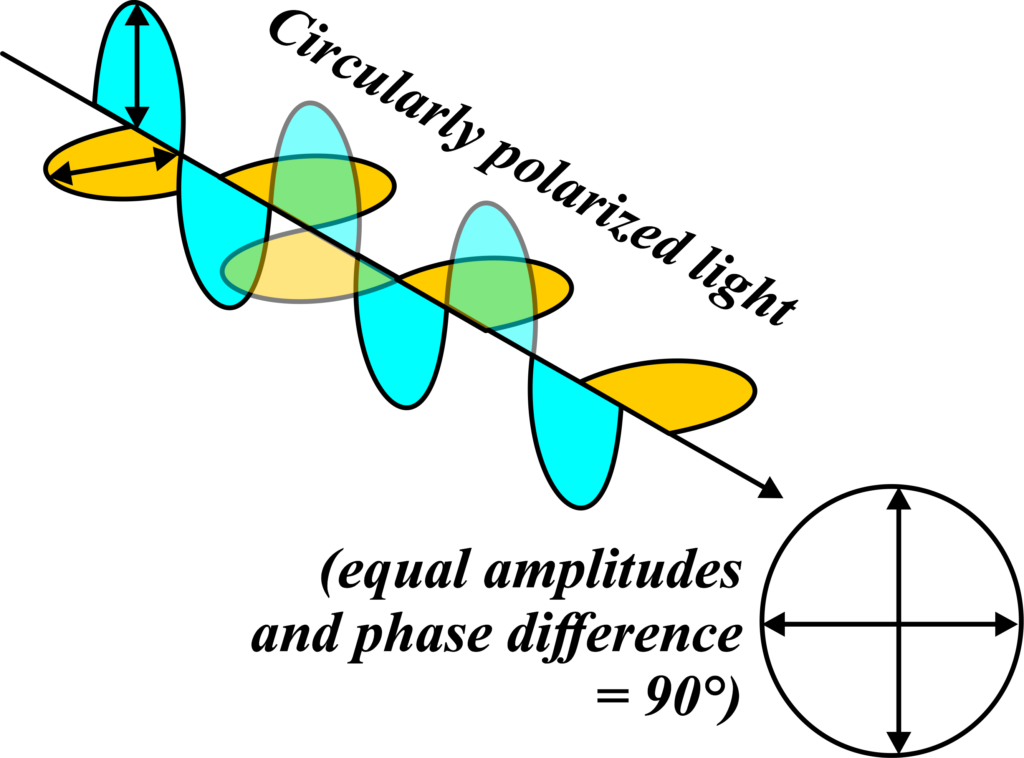
To visualize circular polarization, imagine a string with a small ball attached to its end. If you swing the string in a circular motion, the ball’s path will trace out a circle. Now, if you could do this incredibly fast, and if the ball were a point of light, the path it takes would represent the electric field of a circularly polarized light wave.
In circular polarization, the electric field of the light wave rotates clockwise or counterclockwise around the direction of travel. This rotation can be either:
- Right-handed Circular Polarization (RCP): The electric field rotates clockwise when viewed from the receiver’s perspective.
- Left-handed Circular Polarization (LCP): The electric field rotates counterclockwise when viewed from the receiver’s perspective.
Mathematically, circular polarization can be described by combining two linearly polarized waves that are perpendicular to each other and have a phase difference of 90 degrees. The electric field vector (\(\displaystyle\vec{E}\)) at any point in space can be represented as:
\(\displaystyle \vec{E}(z,t) = E_0 \left[ \cos(kz – \omega t) \hat{i} \pm \sin(kz – \omega t) \hat{j} \right] \)
where (E0) is the amplitude, (k) is the wave number, (ω) is the angular frequency, (\(\displaystyle \hat{i} \)) and (\(\displaystyle \hat{j} \)) are unit vectors in the perpendicular directions, and the (\(\displaystyle \pm \)) sign represents the direction of rotation.
In simpler terms, circular polarization is when the light’s vibrations trace out a circle in space as the wave moves forward. It’s a dynamic and intriguing form of light that’s used in various applications, such as in communication systems and 3D movies, where different circular polarizations are used to create a sense of depth. It’s a dance of light waves, spiraling gracefully as they journey through space.
Elliptical Polarization:
Elliptical polarization is a type of light polarization where the tip of the electric field vector describes an ellipse in a plane perpendicular to the direction of propagation. This might sound complex, but let’s break it down with an analogy.
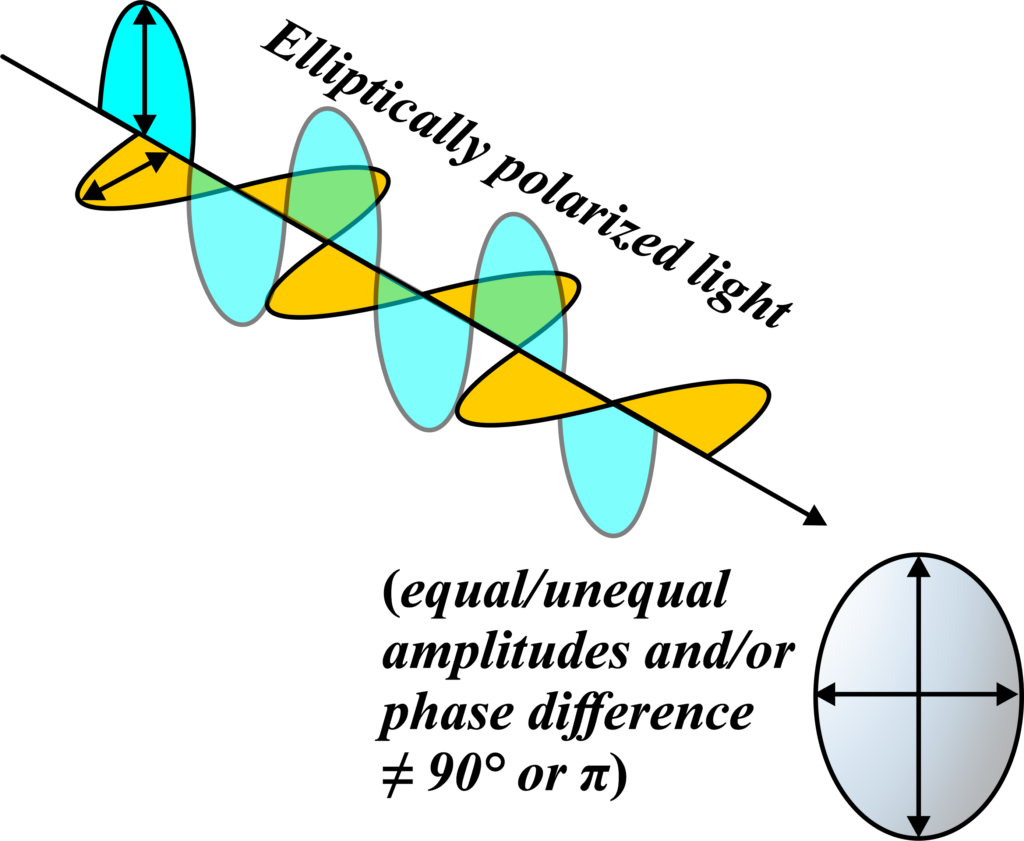
Think of a spinning top. As it spins, the tip of the top draws a circle if it’s perfectly upright. Now, if the top is not spinning upright and is instead tilted, the path it traces becomes an ellipse. This is similar to how elliptically polarized light works.
In elliptical polarization, the electric field of the light wave moves in an elliptical motion.
It’s a combination of both linear and circular polarization. The light wave has components that are vibrating in a linear fashion and components that are rotating, and together, they form an ellipse.
Here’s a simple way to visualize it:
- Imagine a beam of light coming straight towards you.
- As it travels, the electric field ‘wobbles’ in an elliptical shape, rather than just up and down (linear) or in a perfect circle (circular).
Mathematically, elliptical polarization can be described by combining two perpendicular linearly polarized waves with different amplitudes and a phase difference. The electric field (\(\displaystyle \vec{E}\)) can be represented as:
\(\displaystyle \vec{E}(z,t) = E_{0x} \cos(kz – \omega t) \hat{i} + E_{0y} \sin(kz – \omega t + \phi) \hat{j} \)
where (E0x) and (E0y) are the amplitudes of the waves in the x and y directions, (k) is the wave number, (\(\displaystyle \omega \)) is the angular frequency, (Φ) is the phase difference, and ( \(\displaystyle\hat{i} \)) and ( \(\displaystyle\hat{j} \)) are unit vectors in the x and y directions.
In simpler terms, elliptical polarization is when the light’s vibrations create an elliptical pattern as the wave moves forward. It’s a more general form of polarization that includes linear and circular as special cases. It’s like the light is dancing in an elliptical pattern, showing the complex and beautiful nature of electromagnetic waves. Elliptical polarization is another example of the diverse ways in which light can manifest its wave-like properties.
Methods of Polarization of Light
Light can be polarized through several methods:
Polarization by Transmission (Polaroids):
When we talk about the transmission method of polarization, we’re referring to the process where certain materials can filter light waves, allowing only waves that oscillate in a particular direction to pass through.
Imagine you have a set of vertical bars, like a jail cell’s bars. Now, if you try to pass a stick through these bars, you can only do so if the stick is vertical. If you try to pass it horizontally, the bars will block it. This is similar to how polarizing filters work.

A polarizing filter is like those vertical bars but for light waves. It has a series of microscopic lines or structures that are aligned in the same direction. When unpolarized light, which vibrates in all directions, hits this filter, only the light waves that are vibrating parallel to these lines can pass through. The rest are absorbed or reflected.
Here’s a simple analogy: Think of a crowd trying to get through a narrow gate. Only the people moving directly towards the gate can get through easily, while those approaching from an angle have to align themselves to pass.
Polaroids, often referred to in the context of polarizing filters, are materials that can filter out certain orientations of light waves, allowing only waves vibrating in a specific direction to pass through.
- Think of light as a crowd of people all walking in different directions. Now, imagine a gate that only lets people walk through if they’re going straight in one direction—say, north to south.
- Polaroids act like this gate. They have a special coating with molecules aligned in one direction. When light hits this coating, only the waves moving parallel to these molecules can pass through. All other waves are absorbed or blocked.
In technical terms, when unpolarized light encounters a polarizing filter, the electric field component of the light wave that is parallel to the alignment of the filter is transmitted, while the perpendicular component is absorbed. This results in light that is polarized in the direction of the filter’s alignment.
So, the transmission method of polarization is like a selective gate that only allows light waves vibrating in a certain direction to pass through. It’s a key principle behind many optical devices and technologies, such as polarized sunglasses, which reduce glare by filtering out certain orientations of light waves.
Polarization by Reflection :
Polarization by reflection is a process where light becomes polarized after reflecting off a surface at a certain angle. Polarization by reflection is a natural phenomenon that occurs when light bounces off certain surfaces. It’s like when you see sunlight glinting off the surface of a lake. Some of that reflected light is polarized, which means the light waves are aligned in a specific direction.
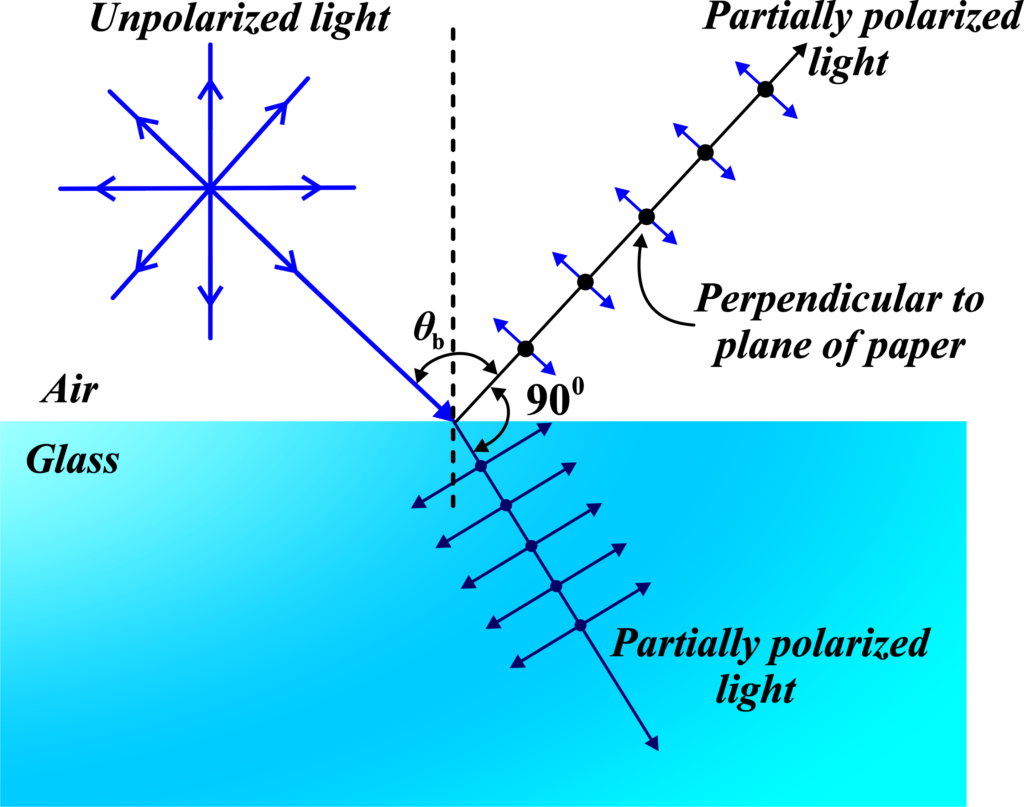
- When light hits a surface at an angle, it doesn’t just bounce off randomly. Instead, the light waves that are vibrating parallel to the surface get absorbed or pass through, while the ones vibrating at other angles are reflected.
- This means the reflected light is now vibrating mostly in one direction—it’s been polarized.
This effect is strongest at a particular angle known as Brewster’s angle. At this angle, the reflected light is completely polarized. Brewster’s angle depends on the material the light is reflecting off of. For example, for water, it’s around 53 degrees.
Analogy to help visualize it: Imagine throwing a bunch of spaghetti noodles at a wall. Some noodles hit the wall head-on and stick, while others hit at an angle and bounce off. The noodles bouncing off are like polarized light—they’ve been sorted into a specific orientation by the wall. It’s a concept that explains why polarized sunglasses can reduce glare from horizontal surfaces like roads and water, making it easier to see on a sunny day.
Polarization by Refraction:
Polarization is a process that can happen when light refracts, or bends, as it moves from one substance into another. This bending changes the light’s path and can give the light a certain level of polarization, typically aligning it perpendicularly to the surface where the refraction occurs.
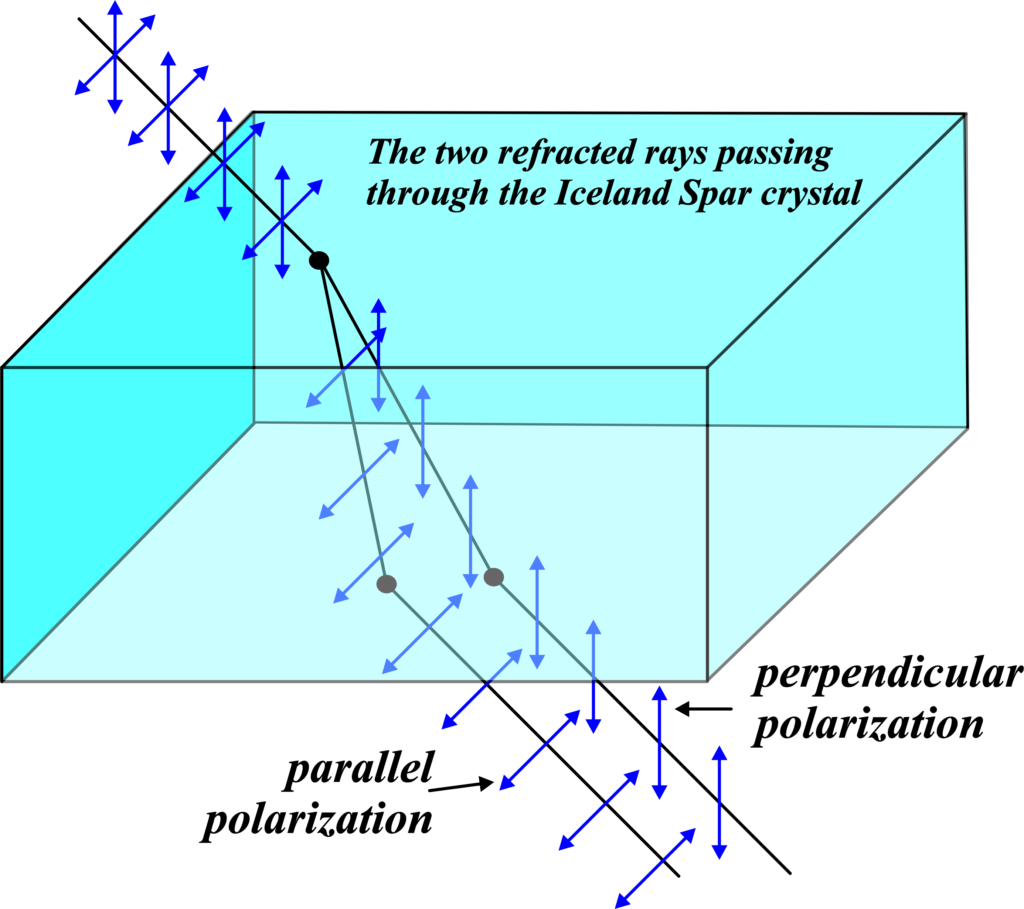
One such crystal is Iceland Spar, a unique variant of calcite, which splits incoming light into two separate beams. When you look through an Iceland Spar crystal, you’ll see double because of this splitting effect. Each of the two beams that come out of the crystal is polarized—one parallel to the surface and the other at a right angle to it.
If you then use a polarizing filter, you can block out one of the doubled images completely. Align the filter so its polarization axis is at a right angle to the direction of the polarized light, and that light will be absorbed by the filter, leaving the other image clear and bright.
Rotate the filter by 90 degrees, and the first image will pop back into view while the second one vanishes. This cool trick is a direct result of light’s wave-like properties, something we wouldn’t be able to see if light behaved differently.
How polarized sunglasses use refraction-based polarization?
Polarized sunglasses utilize the principle of polarization by absorption rather than refraction. Here’s how they work: When light reflects off flat surfaces like water, roads, or snow, it becomes horizontally polarized. This means the light vibrates mainly in a horizontal plane, leading to glare that can be harsh on the eyes.
Polarized sunglasses have a special chemical applied to them that filters light. The filter is made up of molecules that are aligned horizontally. These molecules act like tiny Venetian blinds and block the horizontally polarized light from passing through the lens.
Here’s a simple analogy: Imagine you’re looking through a fence with vertical slats. This fence will block objects moving horizontally, like a frisbee thrown parallel to the slats, but it will allow vertically moving objects, like a bouncing ball, to be seen. Similarly, the polarized filter blocks the horizontal light waves (glare) but allows vertically polarized light to pass through.
So, while refraction can cause some degree of polarization, the polarization that polarized sunglasses use to reduce glare is actually due to absorption by the filter’s molecular structure, not refraction. It’s a clever use of physics to improve comfort and visibility in bright conditions.
Polarization by Scattering:
Scattering is a process where light bounces off particles in the atmosphere, like air molecules or dust, and changes direction. This process can also lead to the polarization of light.
Here’s a straightforward way to understand it:
- When light from the sun enters Earth’s atmosphere, it collides with molecules and small particles.
- These collisions cause the light to scatter in all directions.
- During this scattering process, the light can become polarized, meaning the light waves are more aligned in certain directions.
A good example of this is the blue sky. The reason the sky is blue is due to the scattering of sunlight by the atmosphere. The shorter (blue) wavelengths of light are scattered more than the longer (red) wavelengths. This scattered blue light is also partially polarized.
Here’s an analogy:
- Imagine throwing a ball at a bunch of pins. The ball represents a beam of light, and the pins are the particles in the atmosphere.
- When the ball hits the pins, it bounces off in different directions—this is scattering.
- If you notice the paths of the balls, they tend to become more organized after hitting the pins, similar to how light becomes polarized after scattering.
Polarization by scattering is a process where light becomes partially polarized as it bounces off small particles in the atmosphere. It’s a natural phenomenon that explains why the sky is blue and why we often see beautiful colors during sunrise and sunset. It’s like a cosmic dance where light is scattered and subtly organized by the very air we breathe.
How does the degree of polarization change with different scattering angles?
The degree of polarization of light changes with the scattering angle due to the interaction of light with particles in the atmosphere. When unpolarized light is scattered, the degree of polarization depends on the angle at which the light is scattered.
Here’s a simplified explanation:
- At a scattering angle of 0° (light not deviated from its path), there is no polarization.
- At a scattering angle of 90° (light scattered perpendicular to the original direction), the light is fully polarized.
- For angles between 0° and 90°, the light is partially polarized.
The degree of polarization for light scattered at an angle (θ) to an incident beam of unpolarized radiation can be described by the formula:
\(\displaystyle P(\theta) = \frac{1 – \cos^2(\theta)}{1 + \cos^2(\theta)} \)
In this formula, P(θ) represents the degree of polarization as a function of the scattering angle (θ), and (cos) is the cosine function. As the scattering angle increases from 0° to 90°, the value of (cos2(θ)) decreases, which means that P(θ) increases.
So, the degree of polarization is highest when the light is scattered at right angles to the direction of the incoming light and decreases as the angle moves away from 90°. This is why the sky is most polarized at 90° from the sun.
Polarized Light and Unpolarized Light
Unpolarized Light:
When we talk about unpolarized light, we’re referring to light that vibrates in multiple directions. It’s the most common type of light we encounter in our daily lives, coming from sources like the sun, lamps, and candles.
Here’s a simple way to picture it:
- Imagine a rope with waves moving along it. If the waves on the rope move up and down, left and right, and in all other directions perpendicular to the rope, that’s similar to how unpolarized light behaves.
- In unpolarized light, the electric field (which is part of the light wave) vibrates in many different planes perpendicular to the direction of the wave’s travel.
Think of it like this: If you were in a field with grass blowing in the wind, the grass blades would be moving in all sorts of directions. This is what happens with the electric fields in unpolarized light—they’re all over the place, moving independently of one another.
In technical terms, unpolarized light consists of waves that have random orientations of their electric fields. There’s no specific pattern or alignment to the way they vibrate.
Unpolarized light is a jumble of waves vibrating in random directions. It’s the natural state of most of the light around us before it interacts with filters, reflects off surfaces, or scatters through the atmosphere. Understanding unpolarized light is essential for grasping the basics of light’s wave properties and polarization.
Polarized Light:
To understand polarized light, let’s think about light as a wave—similar to waves on water, but with one key difference: light waves can move in more directions.
Normally, light waves vibrate in many directions perpendicular to their path of travel. This is because they are electromagnetic waves, made up of electric and magnetic fields that oscillate at right angles to each other and to the direction of the wave’s travel.
Now, polarized light is special. It’s light that vibrates in one specific direction. It’s as if we’ve taken all the possible directions the light could vibrate in and chosen just one. This creates a wave that is much more uniform and orderly.
Here’s an analogy: Imagine a crowd of people walking in all directions. This is like unpolarized light. Now, imagine if all these people suddenly started walking in the same direction, in a straight line. That’s what polarized light is like.
In more technical terms, when light is polarized, its electric field oscillates in a single plane along the wave’s direction of travel. If you could see this electric field, it would look like a flat, undulating ribbon moving through space.
Polarized light can be created in several ways, such as by passing light through a polarizing filter, which only allows waves vibrating in a particular direction to pass through, or by reflecting light off surfaces at certain angles.
Polarized light is a form of light with waves that vibrate in a single, well-defined direction. It’s a neat and organized form of light that has many practical applications, from reducing glare in photography to improving visibility in sunglasses.
Also Read: Coherent And Incoherent Addition of Waves
Brewster’s Law
Brewster’s Law states that light will be perfectly polarized upon reflection at a certain angle, known as Brewster’s angle. This angle depends on the refractive indices of the two media involved. It’s named after the Scottish physicist Sir David Brewster who discovered it in the 19th century.
- When light hits a transparent material at a certain angle, known as Brewster’s angle, the reflected light is completely polarized parallel to the surface.
- At this angle, no reflection of light is polarized perpendicular to the surface.
To understand Brewster’s Law, imagine you’re shining a flashlight on a window. Some of the light goes through, and some of it bounces back. If you adjust the angle of the flashlight just right, the light that bounces back will be polarized, meaning it vibrates in one direction.
The formula for Brewster’s angle (θB) is given by:
\(\displaystyle \tan(\theta_B) = \frac{n_2}{n_1} \)
where (n1) is the refractive index of the first medium (from where the light comes), and (n2) is the refractive index of the second medium (into which the light enters).
Consider a light wave hitting a boundary between two media at an incident angle (\theta_i) and refracting into the second medium at an angle (θr).
According to Snell’s Law, the relationship between the angles of incidence and refraction is given by:
\(\displaystyle n_1 \sin(\theta_i) = n_2 \sin(\theta_r) \)
At Brewster’s angle, the reflected and refracted rays are at a right angle to each other. This means:
\(\displaystyle \theta_i + \theta_r = 90^\circ \)
Using trigonometric identities, we know that:
\(\displaystyle \sin(\theta_r) = \cos(\theta_i) \)
Because ( \(\displaystyle\sin(90^\circ – \theta) = \cos(\theta) \)).
Substituting (\(\displaystyle \cos(\theta_i) \)) for ( \(\displaystyle\sin(\theta_r) \)) in Snell’s Law, we get:
\(\displaystyle n_1 \sin(\theta_i) = n_2 \cos(\theta_i) \)
Dividing both sides by ( \(\displaystyle\cos(\theta_i) \)), we obtain:
\(\displaystyle \tan(\theta_i) = \frac{n_2}{n_1} \)
Therefore, Brewster’s angle (θB) is given by:
$$ \theta_B = \arctan\left(\frac{n_2}{n_1}\right) $$
And there you have it! The angle ( \(\displaystyle\theta_B \)) at which the light must strike the surface to be polarized is called Brewster’s angle, and it can be found using the refractive indices of the two media. This angle is where the reflected light is completely polarized parallel to the surface, and no light is reflected in the perpendicular polarization.
So, Brewster’s Law is a neat way to predict the angle for perfect polarization upon reflection, and it’s all based on the relationship between the angles and the properties of the materials the light interacts with. It’s like finding the sweet spot where the light ‘chooses’ to vibrate in just one direction after bouncing off a surface.
Application of Polarisation of Light
Polarization of light is not just a fascinating scientific concept; it has many practical applications that affect our daily lives. Here are some of the key applications explained in a way that’s easy to understand:
- Polarized Sunglasses: These sunglasses have a special coating that blocks horizontally polarized light, which is common in glare from surfaces like water or roads. This helps reduce eye strain and improves visual clarity.
- Photography: Photographers use polarizing filters to manage reflections and suppress glare from surfaces like glass or water. This enhances the color and contrast in the pictures.
- LCD Screens: Liquid Crystal Displays (LCDs) found in watches, calculators, and screens use polarization. They control the light passing through the liquid crystals by aligning or blocking polarized light.
- 3D Movies: Modern 3D cinema technology uses polarization. Two images are projected onto the screen with different polarizations, and the 3D glasses have polarized lenses that allow each eye to see only one of the images, creating a three-dimensional effect.
- Stress Analysis: Polarized light is used in engineering to analyze stress patterns in transparent materials. When polarized light passes through stressed plastic or glass, it shows colorful patterns that indicate where the material is under stress.
- Optical Instruments: Many optical instruments, like microscopes and telescopes, use polarized light to enhance the contrast of the image or to study the properties of light from different celestial objects.
- Communication: Optical fibers use polarized light for transmitting information. The polarization helps in managing the integrity of the signal over long distances.
- Chemistry and Biology: Polarized light helps scientists study molecular structures and biological samples. It can reveal details about the orientation and bonding of molecules.
The applications of polarized light are vast and varied, touching on everything from personal comfort and entertainment to scientific research and communication technology. It’s a powerful tool that helps us see and understand the world in new and exciting ways.
Solved Examples
Problem 1: Calculate the Brewster angle for light reflecting off a glass surface with a refractive index of 1.5.
Solution: Brewster’s Law states that the Brewster angle (θB) is given by:
\(\displaystyle\tan \theta_B = n\)
Substitute the given values:
\(\displaystyle\tan \theta_B = 1.5\)
\(\displaystyle\theta_B = \tan^{-1}(1.5) \approx 56.31^\circ\)
The Brewster angle for light reflecting off a glass surface with a refractive index of 1.5 is approximately ( 56.31∘).
Problem 2: Unpolarized light of intensity (I0) passes through two polarizing filters. The transmission axis of the second filter is at an angle of (30∘) to the transmission axis of the first. What is the intensity of light emerging from the second filter?
Solution: Malus’s Law states that the intensity (I) of light passing through a polarizer is given by:
\(\displaystyle I = I_0 \cos^2 \theta\)
For unpolarized light passing through the first polarizer, the intensity is reduced to (I0/2). For the second polarizer:
\(\displaystyle I = \frac{I_0}{2} \cos^2(30^\circ)\)
\(\displaystyle I = \frac{I_0}{2} \left(\frac{\sqrt{3}}{2}\right)^2\)
\(\displaystyle I = \frac{I_0}{2} \times \frac{3}{4} = \frac{3I_0}{8}\)
The intensity of light emerging from the second filter is (\(\displaystyle \frac{3I_0}{8} \)).
Problem 3: A light ray enters a calcite crystal at an angle of incidence of (45∘). The refractive indices for the ordinary and extraordinary rays are 1.658 and 1.486, respectively. Calculate the angle of refraction for both rays inside the crystal.
Solution: Using Snell’s Law:
\(\displaystyle n_1 \sin \theta_i = n_2 \sin \theta_r\)
For the ordinary ray:
\(\displaystyle 1 \sin 45^\circ = 1.658 \sin \theta_{o}\)
\(\displaystyle \sin \theta_{o} = \frac{\sin 45^\circ}{1.658} = \frac{0.707}{1.658} \approx 0.426\)
\(\displaystyle\theta_{o} = \sin^{-1}(0.426) \approx 25.23^\circ\)
For the extraordinary ray:
\(\displaystyle 1 \sin 45^\circ = 1.486 \sin \theta_{e}\)
\(\displaystyle\sin \theta_{e} = \frac{\sin 45^\circ}{1.486} = \frac{0.707}{1.486} \approx 0.476\)
\(\displaystyle\theta_{e} = \sin^{-1}(0.476) \approx 28.41^\circ\)
The angle of refraction for the ordinary ray is approximately (25.23∘), and for the extraordinary ray, it is approximately (28.41∘).
Problem 4: Two polaroids are oriented with their axes at (60∘) to each other. If unpolarized light of intensity (I0) is incident on the first polaroid, what is the intensity of the light emerging from the second polaroid?
Solution: When unpolarized light passes through the first polaroid, its intensity is reduced to (I0/2). Using Malus’s Law for the second polaroid:
\(\displaystyle I = \frac{I_0}{2} \cos^2(60^\circ)\)
\(\displaystyle I = \frac{I_0}{2} \left(\frac{1}{2}\right)^2\)
\(\displaystyle I = \frac{I_0}{2} \times \frac{1}{4} = \frac{I_0}{8}\)
The intensity of light emerging from the second polaroid is (\(\displaystyle \frac{I_0}{8} \)).
Problem 5: Calculate the Brewster angle for light reflecting off a water surface, given the refractive index of water is 1.33.
Solution: Brewster’s Law:
\(\displaystyle\tan \theta_B = n\)
Substitute the given values:
\(\displaystyle \tan \theta_B = 1.33\)
\(\displaystyle\theta_B = \tan^{-1}(1.33) \approx 53.06^\circ\)
The Brewster angle for light reflecting off a water surface is approximately (53.06∘).
Problem 6: A beam of unpolarized light of intensity (I0) is incident on a polarizer. What fraction of the incident intensity is transmitted through a second polarizer whose axis makes an angle of (45∘) with the first?
Solution: The intensity after the first polarizer is:
\(\displaystyle I_1 = \frac{I_0}{2}\)
Using Malus’s Law for the second polarizer:
\(\displaystyle I = I_1 \cos^2(45^\circ)\)
\(\displaystyle I = \frac{I_0}{2} \cos^2(45^\circ)\)
\(\displaystyle I = \frac{I_0}{2} \left(\frac{1}{\sqrt{2}}\right)^2\)
\(\displaystyle I = \frac{I_0}{2} \times \frac{1}{2} = \frac{I_0}{4}\)
The fraction of the incident intensity transmitted through the second polarizer is (\(\displaystyle \frac{I_0}{4}\)).
FAQs
What is polarization of light and why does it occur?
Polarization of light refers to the orientation of the oscillations of the electric field vector in a light wave. It occurs because light is a transverse wave, meaning the oscillations of the electric and magnetic fields are perpendicular to the direction of wave propagation. Polarization can occur through various processes that align these oscillations in specific directions.
What is the difference between transverse waves and longitudinal waves?
Transverse waves have oscillations that are perpendicular to the direction of wave propagation, such as light waves and water waves. Longitudinal waves have oscillations that are parallel to the direction of wave propagation, such as sound waves. Polarization is a characteristic specific to transverse waves.
What are the different types of polarization of light?
The different types of polarization of light include linear polarization, where the electric field oscillates in a single direction; circular polarization, where the electric field rotates in a circular motion around the direction of propagation; and elliptical polarization, where the electric field describes an ellipse. Each type represents a different state of the oscillation pattern of the light wave.
What is the difference between polarized light and unpolarized light?
Polarized light consists of waves where the electric field oscillates in a single direction or plane. Unpolarized light, on the other hand, consists of waves with electric field oscillations in multiple random directions. Natural sunlight and most artificial light sources emit unpolarized light, while polarized light can be produced through various polarization techniques.
What is Brewster’s Law and how is it related to polarization?
Brewster’s Law states that the angle of incidence at which light is perfectly polarized upon reflection is such that the reflected and refracted rays are perpendicular to each other. This specific angle is known as Brewster’s angle. At this angle, the reflected light is completely polarized parallel to the reflecting surface. Brewster’s Law is used in designing polarizing filters and understanding reflection properties.