The story of springs and their potential energy is a fascinating one that stretches back centuries. Before we had the coiled springs we’re familiar with today, people used leaf springs made of curved metal strips. These were not very efficient and required constant lubrication, plus they were noisy.
The game-changer came in 1763 when R. Tradwell invented the first coiled spring. This invention was revolutionary because coiled springs were much more efficient at storing and releasing energy. They could be compressed or extended and would return to their original shape, ready to be used again.
The understanding of how springs store energy evolved. In the 17th century, Robert Hooke, a British scientist, formulated Hooke’s Law, which describes the relationship between the force applied to a spring and the amount of stretch or compression. This law laid the foundation for understanding the potential energy in springs.
This law is crucial because it tells us that when we compress or extend a spring, we’re doing work on it, and this work is stored as potential energy. The more you stretch or compress the spring, the more energy it stores, ready to be released when the spring returns to its original shape.
Hooke’s Law of Spring Constant
Hooke’s Law is a principle of physics that states the force needed to extend or compress a spring by some distance is proportional to that distance.
Imagine you have a spring, like the one inside a pen. When you press down on the top of the pen, the spring compresses, and when you let go, it bounces back. This is where Hooke’s Law comes into play.
Hooke’s Law tells us that the force it takes to compress or stretch a spring is directly related to how much you compress or stretch it. It’s like pushing a shopping cart; the more you push, the faster it goes. Similarly, the more you stretch or compress a spring, the more force it pushes back.
The spring constant, represented by the letter ( k ), is a number that tells us how stiff the spring is. A higher (k) means a stiffer spring, just like a thicker rubber band is harder to stretch than a thinner one.
The formula for Hooke’s Law is
\(\displaystyle F = -kx \)
- (F) is the force you apply to the spring.
- (k) is the spring constant.
- (x) is the distance you’ve stretched or compressed the spring from its original position.
The negative sign means that the force the spring exerts is in the opposite direction to the way you’re stretching or compressing it. So if you pull a spring, it pulls back; if you push a spring, it pushes back.
Let’s say you have a spring with a spring constant of 500 N/m (which means it’s pretty stiff), and you compress it by 0.2 meters. The force you’re applying to the spring is:
\(\displaystyle F = -500 \, \text{N/m} \times 0.2 \, \text{m} = -100 \, \text{N} \)
This means the spring is pushing back with a force of 100 newtons.
Hooke’s Law is crucial for things like designing car suspensions, mattresses, and even athletic shoes. It’s all about how materials return to their original shape after being stretched or squished.
Potential Energy of Spring
Potential Energy in spring, also known as elastic potential energy, is the energy stored due to the spring’s deformation, such as stretching or compressing. When a spring is not at its equilibrium position, it has the potential to do work because of its position.
A spring’s potential energy is stored when you compress or stretch the spring from its original, relaxed position. It’s like loading a slingshot; the more you pull back, the more energy you store when you let go.
When you compress or stretch a spring, you’re doing work against the spring’s natural tendency to return to its relaxed state. This work gets stored as potential energy. The spring holds onto this energy until it’s released, allowing the spring to snap back to its original shape.
The potential energy (PE) stored in a spring is calculated using this formula:
\(\displaystyle PE = \frac{1}{2} k x^2 \)
Imagine you have a spring with a spring constant (k) of 300 N/m, and you stretch it by 0.2 meters. The potential energy stored in the spring would be:
$$ PE = \frac{1}{2} \times 300 \, \text{N/m} \times (0.2 \, \text{m})^2 $$
$$ PE = \frac{1}{2} \times 300 \, \text{N/m} \times 0.04 \, \text{m}^2 $$
$$ PE = 6 \, \text{J} $$
This means the spring has 6 joules of energy ready to be released when you let go.
The potential energy of a spring is important because it’s a principle that applies to many everyday objects and systems. From the suspension in cars to the bounce in your sneakers, springs and their potential energy play a crucial role. Knowing how to calculate this energy helps us better design and understand these systems.
Work Done by Spring
The work done by a spring is the energy transferred to or from the spring when it is compressed or stretched. It’s calculated using the same formula as the potential energy because the work done on the spring is stored as potential energy.
When we talk about the work done by a spring, we’re referring to the energy transferred when the spring is stretched or compressed. This energy is what we call elastic potential energy, and it’s stored in the spring until it’s released.
To derive the work done by a spring, we start with Hooke’s Law, which tells us the force exerted by a spring is proportional to its displacement:
\(\displaystyle F = -kx \)
Here, (F) is the force exerted by the spring, (k) is the spring constant, and (x) is the displacement from the spring’s equilibrium position. The negative sign indicates that the force exerted by the spring is in the opposite direction of the displacement.
Now, the work done (W) by a force over a displacement is given by the product of the force and the displacement in the direction of the force. Since the force exerted by the spring changes, as it is stretched or compressed, we need to integrate it to find the total work done:
\(\displaystyle W = \int_{0}^{x} -kx \, dx \)
Performing the integration, we get:
\(\displaystyle W = -\frac{1}{2} kx^2 \Big|_{0}^{x} \)
\(\displaystyle W = -\frac{1}{2} kx^2 + \frac{1}{2} k \cdot 0^2 \)
\(\displaystyle W = -\frac{1}{2} kx^2 \)
The work done by the spring is negative, which means that the spring does work on whatever is stretching or compressing it. However, when we talk about the energy stored in the spring, we’re interested in the magnitude of this work, which is positive. So, the elastic potential energy stored in the spring is:
\(\displaystyle PE = \frac{1}{2} kx^2 \)
Example: Consider a spring with a spring constant (k) of 300 N/m that is compressed by 0.1 m. The work done by the spring when it is compressed is:
\(\displaystyle W = \frac{1}{2} \times 300 \, \text{N/m} \times (0.1 \, \text{m})^2 \)
\(\displaystyle W = \frac{1}{2} \times 300 \, \text{N/m} \times 0.01 \, \text{m}^2 \)
W = 1.5 J
This means that 1.5 joules of work is done by the spring, and this is the amount of elastic potential energy stored in the spring.
System of Two Springs in Series
When two springs are connected in series, the overall extension of the system is the sum of the extensions of the individual springs. Here’s how we derive the expression for the equivalent spring constant (keq) of the system.
Hooke’s Law states that the force (F) exerted by a spring is proportional to its extension (x):
\(\displaystyle F = k x\)
Consider two springs with spring constants (k1) and (k2) connected in series. When a force (F) is applied to the system, it causes an extension in both springs. Let the extensions in the springs be (x1) and (x2), respectively.
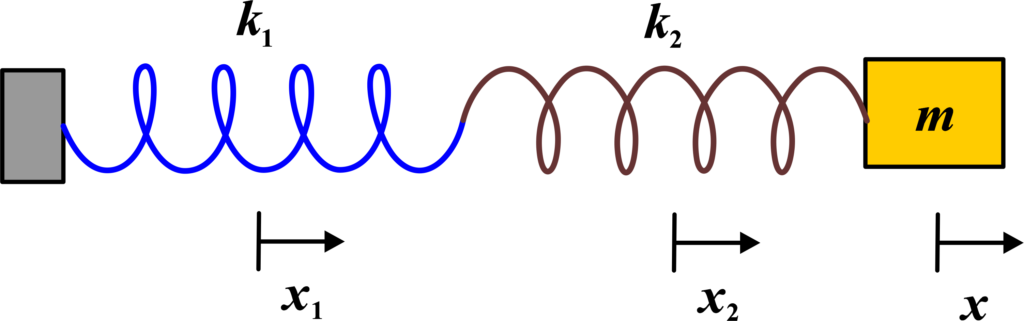
The total extension (x) of the system is the sum of the extensions of the two springs:
\(\displaystyle x = x_1 + x_2\)
Since the springs are in series, the same force (F) acts on both springs. Using Hooke’s Law for each spring:
\(\displaystyle x_1 = \frac{F}{k_1} \quad \text{and} \quad x_2 = \frac{F}{k_2}\)
Substitute (x1) and (x2) into the equation for the total extension:
\(\displaystyle x = \frac{F}{k_1} + \frac{F}{k_2}\)
\(\displaystyle x = F \left( \frac{1}{k_1} + \frac{1}{k_2} \right)\)
According to Hooke’s Law for the equivalent spring, the total extension (x) can also be written as:
\(\displaystyle x = \frac{F}{k_{\text{eq}}}\)
Equate the two expressions for (x):
\(\displaystyle\frac{F}{k_{\text{eq}}} = F \left( \frac{1}{k_1} + \frac{1}{k_2} \right)\)
Divide both sides by (F) (assuming (\(\displaystyle F \neq 0 \))):
\(\displaystyle\frac{1}{k_{\text{eq}}} = \frac{1}{k_1} + \frac{1}{k_2}\)
The equivalent spring constant for two springs in a series is:
\(\displaystyle\frac{1}{k_{\text{eq}}} = \frac{1}{k_1} + \frac{1}{k_2}\)
or equivalently,
\(\displaystyle k_{\text{eq}} = \left( \frac{1}{k_1} + \frac{1}{k_2} \right)^{-1}\)
When springs are connected in series, the same force acts on both springs, but the total extension is the sum of the extensions of each spring. The equivalent spring constant (keq) for springs in series can be found by summing the reciprocals of the individual spring constants and then taking the reciprocal of the sum.
System of Two Springs in Parallel
When two springs are connected in parallel, they share the same extension but the forces exerted by them add up. Here’s how we derive the expression for the equivalent spring constant (keq) of the system.
Consider two springs with spring constants (k1) and (k2) connected in parallel. When a force (F) is applied to the system, it is distributed between the two springs. Let the extensions in both springs be (x).
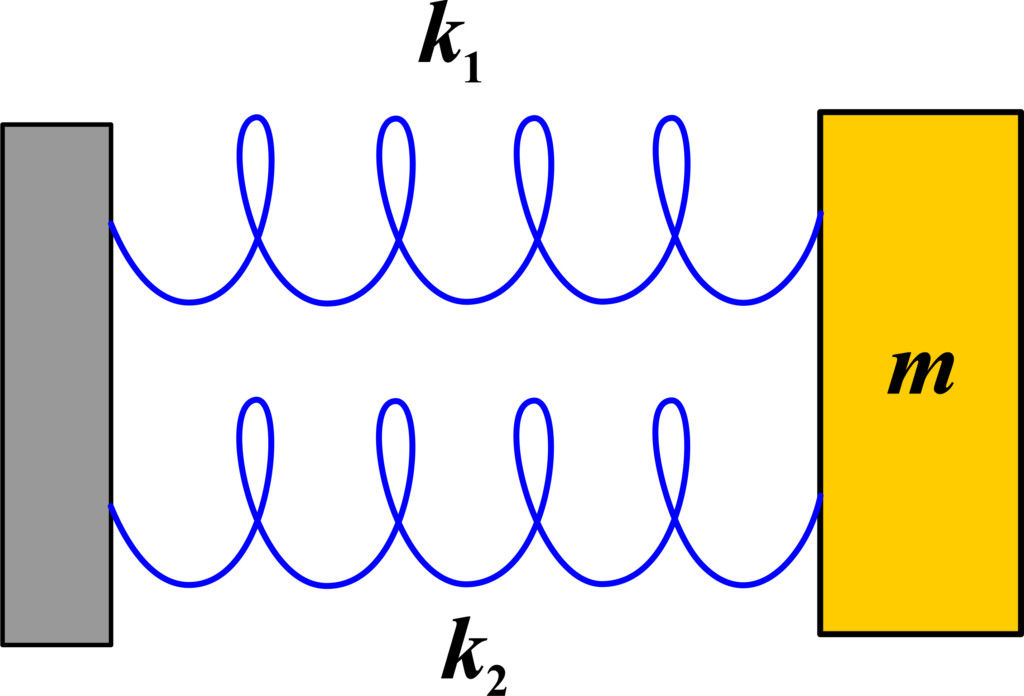
Since the springs are in parallel, the total force (F) is the sum of the forces in the individual springs:
\(\displaystyle F = F_1 + F_2\)
where: \(\displaystyle F_1 = k_1 x \quad \text{and} \quad F_2 = k_2 x\)
Substitute (F1) and (F2) into the equation for the total force:
\(\displaystyle F = k_1 x + k_2 x\)
\(\displaystyle F = (k_1 + k_2) x\)
According to Hooke’s Law for the equivalent spring, the total force (F) can also be written as:
\(\displaystyle F = k_{\text{eq}} x\)
Equate the two expressions for (F):
\(\displaystyle k_{\text{eq}} x = (k_1 + k_2) x\)
Divide both sides by (x) (assuming (\(\displaystyle x \neq 0 )\)):
\(\displaystyle k_{\text{eq}} = k_1 + k_2\)
The equivalent spring constant for two springs in parallel is:
\(\displaystyle k_{\text{eq}} = k_1 + k_2\)
When springs are connected in parallel, they have the same extension, but the forces they exert add up. The equivalent spring constant (keq) for springs in parallel is simply the sum of the individual spring constants.
Energy Stored in Parallel Springs
When two springs are connected in parallel, they share the same extension but the forces they exert add up. We’ll derive the expression for the total energy stored in this system.
The equivalent spring constant (keq) for springs in parallel is:
\(\displaystyle k_{\text{eq}} = k_1 + k_2\)
The potential energy stored in each spring is:
\(\displaystyle U_1 = \frac{1}{2} k_1 x^2\)
\(\displaystyle U_2 = \frac{1}{2} k_2 x^2\)
The total energy (Utotal) stored in the system of parallel springs is the sum of the energies stored in the individual springs:
\(\displaystyle U_{\text{total}} = U_1 + U_2\)
Substituting the expressions for (U1) and (U2):
\(\displaystyle U_{\text{total}} = \frac{1}{2} k_1 x^2 + \frac{1}{2} k_2 x^2\)
Factor out the common term (\(\displaystyle\frac{1}{2} x^2\)):
\(\displaystyle U_{\text{total}} = \frac{1}{2} x^2 (k_1 + k_2)\)
Recall that (\(\displaystyle k_{\text{eq}} = k_1 + k_2 \)). Substitute this into the total energy expression:
\(\displaystyle U_{\text{total}} = \frac{1}{2} x^2 k_{\text{eq}}\)
The energy stored in a system of two springs connected in parallel is:
\(\displaystyle U_{\text{total}} = \frac{1}{2} k_{\text{eq}} x^2\)
where (\(\displaystyle k_{\text{eq}} = k_1 + k_2 \)).
When springs are connected in parallel, they have the same extension, but the forces they exert add up. The energy stored in each spring depends on its spring constant and the square of its extension. The total energy stored in the parallel spring system is the sum of the energies stored in the individual springs, which can be expressed using the equivalent spring constant.
Also Read: Elastic Moduli
Solved Examples
Problem 1: A spring with a spring constant (k = 200 N/m) is compressed by 0.1 meters. Calculate the potential energy stored in the spring.
Solution: The potential energy (U) stored in a spring compressed or stretched by a distance (x) is given by:
\(\displaystyle U = \frac{1}{2} k x^2 \)
Given: k = 200 N/m; x = 0.1 m.
Substitute the values into the formula:
\(\displaystyle U = \frac{1}{2} \times 200 \times (0.1)^2 \)
\(\displaystyle U = \frac{1}{2} \times 200 \times 0.01 \)
\(\displaystyle U = \frac{1}{2} \times 2 \)
U = 1 J
The potential energy stored in the spring is 1 J.
Problem 2: A force of 50 N is required to stretch a spring by 0.25 meters. Determine the spring constant (k).
Solution: Hooke’s Law states: F = k x
Given: F = 50 N; x = 0.25 m.
Rearrange the formula to solve for (k):
\(\displaystyle k = \frac{F}{x} \)
\(\displaystyle k = \frac{50}{0.25} \)
k = 200 N/m
The spring constant (k) is 200 N/m.
Problem 3: A spring with a spring constant (k = 150 N/m) is stretched by 0.2 meters. Calculate the work done by the spring.
Solution: The work done (W) by a spring is given by:
\(\displaystyle W = \frac{1}{2} k x^2 \)
Given: k = 150 N/m; x = 0.2 m.
Substitute the values into the formula:
\(\displaystyle W = \frac{1}{2} \times 150 \times (0.2)^2 \)
\(\displaystyle W = \frac{1}{2} \times 150 \times 0.04 \)
\(\displaystyle W = \frac{1}{2} \times 6 \)
W = 3 J
The work done by the spring is 3 J.
Problem 4: A block of mass 2 kg slides on a frictionless surface and collides with a spring of spring constant (k = 500 N/m). If the block’s initial velocity is (3 m/s), find the maximum compression of the spring.
Solution: The kinetic energy (Ek) of the block is converted into the potential energy (U) of the spring.
\(\displaystyle \frac{1}{2} m v^2 = \frac{1}{2} k x^2 \)
Given: m = 2 kg; v = 3 m/s; k = 500 N/m.
Equate the kinetic and potential energy:
\(\displaystyle \frac{1}{2} \times 2 \times 3^2 = \frac{1}{2} \times 500 \times x^2 \)
\(\displaystyle 9 = 250 x^2 \)
\(\displaystyle x^2 = \frac{9}{250} \)
\(\displaystyle x = \sqrt{\frac{9}{250}} \)
\(\displaystyle x = \sqrt{0.036} \)
x = 0.19 m
The maximum compression of the spring is 0.19 meters.
Problem 5: Two springs with spring constants (k1 = 300 N/m) and (k2 = 600 N/m) are connected in series. Calculate the equivalent spring constant (keq) of the system.
Solution: For springs in series, the equivalent spring constant (keq) is given by:
\(\displaystyle \frac{1}{k_{eq}} = \frac{1}{k_1} + \frac{1}{k_2} \)
Given: k1 = 300 N/m; k2 = 600 N/m.
Substitute the values:
\(\displaystyle \frac{1}{k_{eq}} = \frac{1}{300} + \frac{1}{600} \)
\(\displaystyle \frac{1}{k_{eq}} = \frac{2}{600} + \frac{1}{600} \)
\(\displaystyle \frac{1}{k_{eq}} = \frac{3}{600} \)
\(\displaystyle k_{eq} = \frac{600}{3} \)
\(\displaystyle k_{eq} = 200 \, \text{N/m} \)
The equivalent spring constant of the system is 200 N/m.
Problem 6: Two springs with spring constants (k1 = 100 N/m) and (k2 = 200 N/m) are connected in parallel. If the springs are compressed by 0.05 meters, find the total energy stored in the springs.
Solution: For springs in parallel, the total energy stored is the sum of the individual energies stored in each spring.
\(\displaystyle U_{total} = U_1 + U_2 \)
\(\displaystyle U_1 = \frac{1}{2} k_1 x^2 \)
\(\displaystyle U_2 = \frac{1}{2} k_2 x^2 \)
Given: k1 = 100 N/m; k2 = 200 N/m; x = 0.05 m.
Calculate the energies:
\(\displaystyle U_1 = \frac{1}{2} \times 100 \times (0.05)^2 \)
\(\displaystyle U_1 = \frac{1}{2} \times 100 \times 0.0025 \)
U1 = 0.125 J
\(\displaystyle U_2 = \frac{1}{2} \times 200 \times (0.05)^2 \)
\(\displaystyle U_2 = \frac{1}{2} \times 200 \times 0.0025 \)
U2 = 0.25 J
\(\displaystyle U_{total} = 0.125 + 0.25 \)
\(\displaystyle U_{total} = 0.375 \, \text{J} \)
The total energy stored in the springs is 0.375 J.
FAQs
What is the potential energy of a spring, and how is it related to Hooke’s Law?
A spring’s potential energy is stored in the spring when it is compressed or stretched from its equilibrium position. It is directly related to Hooke’s Law, which states that the force exerted by a spring is proportional to the displacement from its equilibrium position. The potential energy stored in the spring is equal to \(\displaystyle\frac{1}{2} kx^2 \).
Can you explain how the potential energy of a spring changes with displacement?
As a spring is compressed or stretched from its equilibrium position, its potential energy increases. This increase in potential energy is proportional to the square of the displacement from equilibrium, as described by the formula \(\displaystyle \frac{1}{2} kx^2 \). The more the spring is compressed or stretched, the greater the potential energy stored in it.
How does the spring constant affect the potential energy stored in a spring?
The spring constant (k) determines the stiffness of the spring. A higher spring constant indicates a stiffer spring, while a lower spring constant indicates a more flexible spring. The potential energy stored in the spring is directly proportional to the square of the displacement and the spring constant, so a higher spring constant results in greater potential energy for the same displacement.
Can the potential energy of a spring be negative?
In most cases, the potential energy of a spring is considered to be zero at its equilibrium position. However, it can become negative if the reference point is chosen differently. For example, if the equilibrium position is considered to have a higher potential energy than a stretched or compressed position, then the potential energy at the equilibrium position would be negative relative to the other positions.
How is the potential energy of a spring related to mechanical work?
The potential energy of a spring is directly related to the mechanical work done on the spring to compress or stretch it from its equilibrium position. The work done on the spring to change its displacement is stored as potential energy in the spring. Conversely, the potential energy can be converted back into mechanical work when the spring returns to its equilibrium position.
Can the potential energy of a spring be converted into other forms of energy?
Yes, the potential energy stored in a spring can be converted into other forms of energy, such as kinetic energy or thermal energy. For example, when a compressed spring is released, its potential energy is converted into kinetic energy as it accelerates an object attached to it.
How does understanding the potential energy of a spring contribute to engineering and design?
Understanding the potential energy of a spring is crucial in various engineering and design applications. Engineers use this knowledge to design systems and devices that utilize the energy stored in springs, such as shock absorbers, car suspensions, and mechanical toys. By calculating and manipulating the potential energy of springs, engineers can optimize the performance and efficiency of these systems.
Very good work