Radioactivity

The discovery of radioactivity was a serendipitous event that marked a significant milestone in the field of physics. It all began with Henri Becquerel, a French physicist who, in 1896, was investigating the properties of phosphorescent materials. He was particularly interested in whether phosphorescent materials, such as certain uranium salts, emitted X-rays after being exposed to sunlight.

Becquerel wrapped a photographic plate in black paper and placed the uranium salts on top. Expecting that only sunlight could cause the salts to emit rays that would fog the plate, he left the setup in a drawer to expose it to sunlight. However, the weather turned cloudy, and he couldn’t proceed with his experiment as planned.

When he later developed the photographic plate, which had not been exposed to sunlight, he was surprised to find that it was fogged. This meant that the uranium salts emitted some form of rays on their own, without any external trigger like sunlight. This spontaneous emission of rays was what Becquerel had discovered, and he called it “radioactivity.”

Following Becquerel’s discovery, two of his colleagues, Marie Curie and Pierre Curie, took an interest in this phenomenon. Marie Curie coined the term “radioactivity” and, along with her husband, began researching materials that exhibited this property. They discovered two new radioactive elements, polonium, and radium, which were far more radioactive than uranium.

The Curies’ work laid the foundation for the understanding of radioactivity and its potential applications. Their research showed that radioactivity was not the result of a chemical reaction but came from within the atom itself, indicating that atoms had a more complex structure than previously thought.

This discovery opened the door to a new era of physics, leading to the development of quantum theory and the exploration of nuclear energy. The study of radioactivity also led to advancements in medicine, such as the use of radium to treat cancer.

What is Radioactivity?

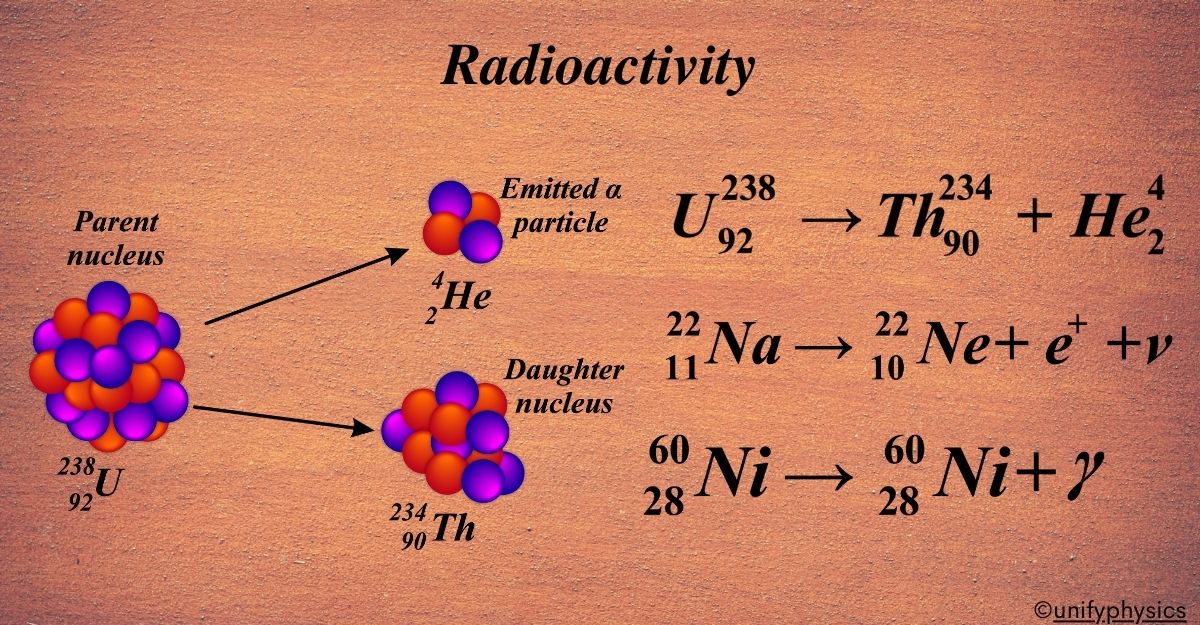
Radioactivity is the spontaneous emission of particles or energy from an unstable atomic nucleus. Imagine an atom as a tiny, bustling city. At the center of this city is the nucleus, which is like the city hall. Just like a city hall, the nucleus is the core of the atom where most of its mass and positive charge are concentrated. Now, in a stable city, everything runs smoothly, but sometimes, the city hall might become too crowded or imbalanced. In the atomic world, this happens when the nucleus has too many protons and neutrons, making it unstable.

When the atomic nucleus is unstable, it wants to get back to a balanced state, just like a city would want to resolve any issues at its core. To do this, the nucleus undergoes a process called radioactivity, where it emits energy and particles to reach a more stable state. This is similar to a city restructuring itself to become more stable and efficient.

In the process of radioactivity, the nucleus can emit three types of particles: alpha particles, which are like the big buses leaving the city carrying a lot of people (in this case, two protons and two neutrons); beta particles, which are like cars leaving the city with just one or two people (here, an electron or positron); and gamma rays, which are like the broadcast signals sent out from the city hall, carrying no passengers but lots of energy.

The important thing to remember is that radioactivity is a natural way for an atom to become more stable. It’s not something that the atom decides to do; it’s a spontaneous process that happens when the conditions within the nucleus are just right.

So, radioactivity is the atomic nucleus’s way of getting back to a balanced state by emitting particles and energy. It’s a natural and spontaneous process that plays a crucial role in the universe, from the stars in the sky to the elements on Earth.

Causes of Radioactivity

Atoms are made up of a nucleus containing protons and neutrons, surrounded by electrons. The protons are positively charged, and the neutrons have no charge. Because like charges repel each other, you might wonder why the protons in the nucleus don’t just push each other apart. The answer lies in what we call the strong nuclear force. This is a powerful force that acts between the protons and neutrons in the nucleus, holding it together despite the repulsive electrostatic forces between the protons.

Now, for most atoms, this balance between the electrostatic repulsion and the strong nuclear force is just right, and the nucleus is stable. However, when an atom has either too many protons or too many neutrons, this balance is disrupted. The nucleus becomes unstable, and this instability is what leads to radioactivity.

In an unstable nucleus, the forces are not in harmony. The nucleus may be too heavy, or the proportion of protons to neutrons may be off. To regain stability, the nucleus will get rid of the excess energy or particles. This is done through radioactive decay, where the nucleus emits particles or energy in the form of radiation.

For example, heavy elements like uranium or plutonium have naturally unstable and very large nuclei. They are constantly trying to reach a more stable state by emitting alpha particles (which are essentially helium nuclei), beta particles (which are electrons), or gamma rays (which are high-energy photons).

The cause of radioactivity is the quest for stability within an atom’s nucleus. When the delicate balance of forces within the nucleus is upset, the atom becomes radioactive as it tries to find a more stable configuration. Radioactivity is the result of an unstable atomic nucleus releasing energy and particles to achieve a more stable state.

Radioactive Radiations

There are three types of radioactive radiation:

Alpha rays (Helium nuclei):

Alpha rays, or alpha particles, are a type of radiation that is commonly emitted by certain radioactive materials. These particles are essentially helium nuclei, which means they consist of two protons and two neutrons bound together. This is the same as the nucleus of a helium atom but without the surrounding electrons.

Now, why are they called rays if they’re particles? Well, when alpha particles are emitted from a radioactive substance, they travel through space, and it’s this movement that was originally described as a ‘ray’. Think of it like a tiny, invisible bullet being shot out from the nucleus of an atom.

Alpha particles are quite hefty in the world of subatomic particles. Because of their relatively large size, they don’t travel very far from their source and can be stopped by just a sheet of paper or even the outer layer of human skin. However, if alpha-emitting materials are ingested or inhaled, they can be harmful because they have a high ability to ionize atoms in the body, which can damage biological tissues.

In the classroom, we might demonstrate the properties of alpha particles by using a radioactive source, a detector, and some material like paper or aluminum foil to show how easily they are stopped. This helps students visualize the concept of alpha radiation and understand its limited range but high ionizing power.

Alpha rays are streams of helium nuclei emitted by unstable atomic nuclei during radioactive decay. They have a short range and are highly ionizing, which makes them both interesting and important to understand in the study of radioactivity.

Beta rays (Electrons):

Beta rays, or beta particles, are one of the types of radiation that an unstable nucleus can emit as it seeks stability. These particles are essentially high-speed electrons (or their antimatter counterparts, positrons, in the case of beta-plus decay).

Beta-minus (β−) decay: This occurs when a neutron in the nucleus turns into a proton and emits an electron. The atom’s atomic number increases by one because of the additional proton, but the mass number stays the same since a neutron and a proton have nearly the same mass. The emitted electron is what we call a beta particle.

Beta-plus (β+) decay: This is the opposite process, where a proton is transformed into a neutron, and a positron (the electron’s antimatter twin) is emitted. The atomic number decreases by one, but again, the mass number remains unchanged.

Beta particles are more penetrating than alpha particles; they can pass through paper and are stopped by materials like aluminum. However, they are less penetrating than gamma rays, which can pass through several centimeters of lead.

In beta decay, there’s also the emission of a neutrino or an antineutrino—extremely light, neutral particles that rarely interact with matter.

Here’s an example of beta-minus decay:

\(\displaystyle ^{14}{6}C \rightarrow ^{14}{7}N + e^- + \bar{\nu}_e \)

In this equation, a carbon-14 atom emits a beta particle (electron) and an antineutrino, transforming into nitrogen-14.

And for beta-plus decay:

\(\displaystyle ^{22}{11}Na \rightarrow ^{22}{10}Ne + e^+ + \nu_e \)

Here, a sodium-22 atom emits a positron and a neutrino, becoming neon-22.

Beta rays are fast-moving electrons or positrons emitted by certain types of radioactive decay. They play a crucial role in the transmutation of elements and are more penetrating than alpha particles but less so than gamma rays.

Gamma rays (High-energy photons):

Gamma rays are a form of electromagnetic radiation, just like the light we see every day, but they are much more powerful. They are at the end of the electromagnetic spectrum, which means they have the shortest wavelengths and the highest frequencies.

Think of gamma rays as the superheroes of the electromagnetic spectrum; they have the most energy and can travel through many materials that stop other types of radiation. For example, gamma rays can pass through the human body, which is why they are used in medical imaging to see inside the body without surgery.

Gamma rays are produced in several ways, but most commonly in the decay of radioactive nuclei. This is what happens after an unstable nucleus emits an alpha or beta particle; the nucleus is often left in an excited state with extra energy. To get rid of this energy and reach a stable state, the nucleus emits a gamma ray.

Here’s a scientific example: When a cobalt-60 nucleus undergoes beta decay, it transforms into a nickel-60 nucleus in an excited state. This excited nickel-60 nucleus then emits a gamma ray to release its excess energy and become stable.

Gamma rays are not made of matter like alpha and beta particles; they are packets of energy called photons. Because they are so energetic, gamma rays can be dangerous; they can damage living cells and are a form of ionizing radiation. However, when used carefully, they can also be beneficial, such as in treating cancer or sterilizing medical equipment.

Gamma rays are high-energy photons that are part of the electromagnetic spectrum. They are produced by the decay of radioactive nuclei and have important applications in medicine and industry due to their ability to penetrate materials and carry a lot of energy.

Law of Radioactive Decay

The law states that the rate at which a radioactive substance decays – meaning the number of atoms that break down and emit radiation – is proportional to the number of unstable atoms present at any given time.

Imagine you have a large collection of identical clocks, and each clock has an alarm set to go off at a random time. You can’t predict when any single clock’s alarm will ring, but with so many clocks, you can predict how many will ring in a given hour. Similarly, in a sample of radioactive atoms, we can’t predict when any single atom will decay, but we can predict how many will decay over a certain period.

We start with the idea that the rate at which the atoms decay is proportional to the number of atoms present. This can be written as:

\(\displaystyle\frac{dN}{dt} = -\lambda N\)

Here, (N) is the number of undecayed atoms at a given time, ( \(\displaystyle\frac{dN}{dt} \)) is the rate of decay (how fast the atoms are decaying), and (λ) is the decay constant, which tells us the probability of an atom decaying per unit time.

The negative sign indicates that the number of undecayed atoms decreases over time. To find out how many atoms remain undecayed after a certain time, we need to integrate this equation. We separate the variables and integrate both sides:

\(\displaystyle\int \frac{1}{N} dN = -\lambda \int dt\)

After integrating, we get:

\(\displaystyle\ln N = -\lambda t + C\)

Where (C) is the integration constant. To find (C), we use the initial condition that at time (t = 0), the number of undecayed atoms is (N_0). So, (\(\displaystyle\ln N_0 = C\)).

Substituting (C) back into our equation gives us:

\(\displaystyle\ln N = -\lambda t + \ln N_0\)

To make this equation more manageable, we exponentiate both sides to remove the natural logarithm:

\(\displaystyle e^{\ln N} = e^{-\lambda t + \ln N_0}\)

This simplifies to:

\(\displaystyle N = N_0 e^{-\lambda t}\)

And there we have it! This is the mathematical expression for the Law of Radioactive Decay. It tells us that the number of undecayed atoms in a sample decreases exponentially over time, at a rate determined by the decay constant (λ). This law helps us understand and calculate the behavior of radioactive materials over time, which is crucial in fields like nuclear physics, medicine, and archaeology.

Laws of Radioactivity:

• Radioactive Decay is a Nucleus Property: Radioactivity is a result of changes in the nucleus of an atom. It’s not influenced by external factors like temperature or pressure.
• Decay Rate is Consistent: The rate at which a radioactive substance decays is constant over time and is independent of the physical or chemical state of the substance.
• Conservation Laws Apply: Radioactive decay obeys fundamental conservation laws, including the conservation of energy, momentum, angular momentum, and electric charge. This means that the total amount of these quantities remains the same before and after a decay process.
• Transformation of Elements: When an atom undergoes radioactive decay, it transforms into a different element or a different isotope of the same element. This new ‘daughter’ nucleus has different physical and chemical properties than the original ‘parent’ nucleus.
• Emission of Particles and Energy: Radioactive decay is always accompanied by the emission of particles (like alpha and beta particles) or energy in the form of gamma rays.
• Rate of Decay Depends on Quantity: The rate at which a radioactive substance decays is directly proportional to the number of radioactive atoms present at that time.

These laws help us predict the behavior of radioactive materials and are fundamental to various applications, from medical treatments to archaeological dating.

Units of Radioactivity

Units of radioactivity are used to measure the activity of a radioactive substance, which is the rate at which the substance undergoes radioactive decay.

The SI unit of radioactivity is the Becquerel (Bq). It’s named after Henri Becquerel, who discovered radioactivity. One Becquerel is defined as the activity of a quantity of radioactive material in which one nucleus decays per second. So, if you have a sample of a radioactive substance and one atom decays every second, that sample has an activity of 1 Bq.

In mathematical terms:

\(\displaystyle 1 \text{ Bq} = 1 \text{ decay per second}\)

There’s also a non-SI unit called the Curie (Ci), which was historically the first unit of radioactivity and is still used in some contexts. It’s named after the famous scientists Marie and Pierre Curie, who conducted pioneering research in radioactivity. One Curie is a much larger unit than one Becquerel:

\(\displaystyle 1 \text{ Ci} = 3.7 \times 10^{10} \text{ decays per second}\)

This means that a sample with an activity of 1 Ci is undergoing 37 billion decays every second, which indicates a very high level of radioactivity.

Another unit sometimes mentioned is the Rutherford (Rd), where:

\(\displaystyle 1 \text{ Rd} = 10^6 \text{ decays per second}\)

Understanding these units helps us quantify the intensity of radioactivity of a substance, which is crucial for safe handling and application in various fields such as medicine and nuclear energy.

Half-Life in Radioactivity

The term “half-life” refers to the amount of time it takes for half of the atoms in a radioactive sample to decay. It’s a measure of the stability of a radioactive isotope and an indicator of how quickly or slowly a substance undergoes radioactive decay.

To put it simply, if you start with a certain amount of a radioactive substance, after one half-life, you’ll have half of that amount left. After another half-life, you’ll have half of the remaining amount, and so on. This process continues until the substance is no longer radioactive.

The concept of half-life is important because it helps scientists understand the behavior of radioactive materials, predict how long they will remain active, and determine safe handling procedures. It’s also used in techniques like radiocarbon dating, which allows archaeologists to determine the age of ancient artifacts.

To derive the expression for half-life in radioactivity, which is a concept that’s crucial for understanding how radioactive substances change over time, let’s start with the law of radioactive decay and then find the half-life from there. We know from the law of radioactive decay that the number of undecayed nuclei (N) at any time (t) is given by:

\(\displaystyle N(t) = N_0 e^{-\lambda t}\)

(N₀) is the initial number of nuclei,
(λ) is the decay constant,
(e) is the base of the natural logarithm.

The half-life (T_1/2) is the time it takes for half of the radioactive nuclei to decay. This means that N(t) at (T_1/2) is half of (N₀):

\(\displaystyle N(T_{1/2}) = \frac{N_0}{2}\)

Substituting this into the decay equation gives us:

\(\displaystyle\frac{N_0}{2} = N_0 e^{-\lambda T_{1/2}}\)

Dividing both sides by (N₀) and taking the natural logarithm of both sides, we get:

\(\displaystyle\ln\left(\frac{1}{2}\right) = -\lambda T_{1/2}\)

Since (\(\displaystyle \ln\left(\frac{1}{2}\right) \)) is the same as (\(\displaystyle -\ln(2) \)), we can write:

\(\displaystyle -\ln(2) = -\lambda T_{1/2}\)

Solving for (T_1/2), we find:

\(\displaystyle T_{1/2} = \frac{\ln(2)}{\lambda}\)

This is the expression for the half-life in terms of the decay constant. It tells us that the half-life is the natural logarithm of 2 divided by the decay constant, which is a fixed value for each radioactive substance. In simpler terms, the half-life is the time it takes for the amount of a radioactive substance to decrease by half, and it’s directly related to how quickly the substance decays.

Example: Iodine-131 is a radioisotope commonly used in medical diagnostics and treatment, particularly for thyroid conditions. It has a half-life of 8 days. This means that every 8 days, the amount of Iodine-131 in a sample will reduce by half due to radioactive decay.

Let’s say we start with a 10-gram sample of Iodine-131. Using the half-life expression:

\(\displaystyle T_{1/2} = \frac{\ln(2)}{\lambda} \)

Given that the half-life (T_1/2) is 8 days, we can calculate the decay constant (λ) as follows:

\(\displaystyle \lambda = \frac{\ln(2)}{T_{1/2}} = \frac{\ln(2)}{8 \text{ days}} \)

Now, after one half-life (8 days), the remaining amount of Iodine-131 will be:

\(\displaystyle N = \frac{N_0}{2} = \frac{10 \text{ g}}{2} = 5 \text{ g} \)

After two half-lives (16 days), the amount left will be:

\(\displaystyle N = \frac{N_0}{2^2} = \frac{10 \text{ g}}{4} = 2.5 \text{ g} \)

And after three half-lives (24 days), the amount will be:

\(\displaystyle N = \frac{N_0}{2^3} = \frac{10 \text{ g}}{8} = 1.25 \text{ g} \)

This pattern continues, with the amount of Iodine-131 decreasing by half every 8 days.

There are many radioisotopes with interesting half-lives, each with its unique applications and characteristics. Here are a few notable examples:

• Carbon-14 (C-14): With a half-life of about 5730 years, it’s used in radiocarbon dating to determine the age of organic materials.
• Uranium-238 (U-238): It has a half-life of 4.5 billion years and is used to date rocks and the age of the Earth.
• Uranium-235 (U-235): This isotope has a half-life of 700 million years and is used as nuclear reactor fuel.
• Cobalt-60 (Co-60): With a half-life of 5.3 years, it’s used in medicine as an external radiation source for cancer treatment.
• Iodine-131 (I-131): It has a half-life of 8.1 days and is used in medical diagnostics and treatment for thyroid conditions.
• Technetium-99m (Tc-99m): This isotope has a very short half-life of only 6 hours, making it ideal for medical imaging because it minimizes radiation exposure.

These half-lives range from hours to billions of years, demonstrating the diversity of radioisotopes and their potential uses in science and industry.

Alpha Decay

Alpha decay is a type of radioactive decay where an unstable atomic nucleus releases an alpha particle and transforms into a new nucleus. Imagine a heavy nucleus in an atom, like a crowded bus that’s too full. To make it more comfortable, a few people need to get off. In the case of a nucleus, it’s not people but a cluster of particles that gets ‘off the bus’. This cluster is what we call an alpha particle, which is made up of two protons and two neutrons, the same as a helium-4 nucleus.

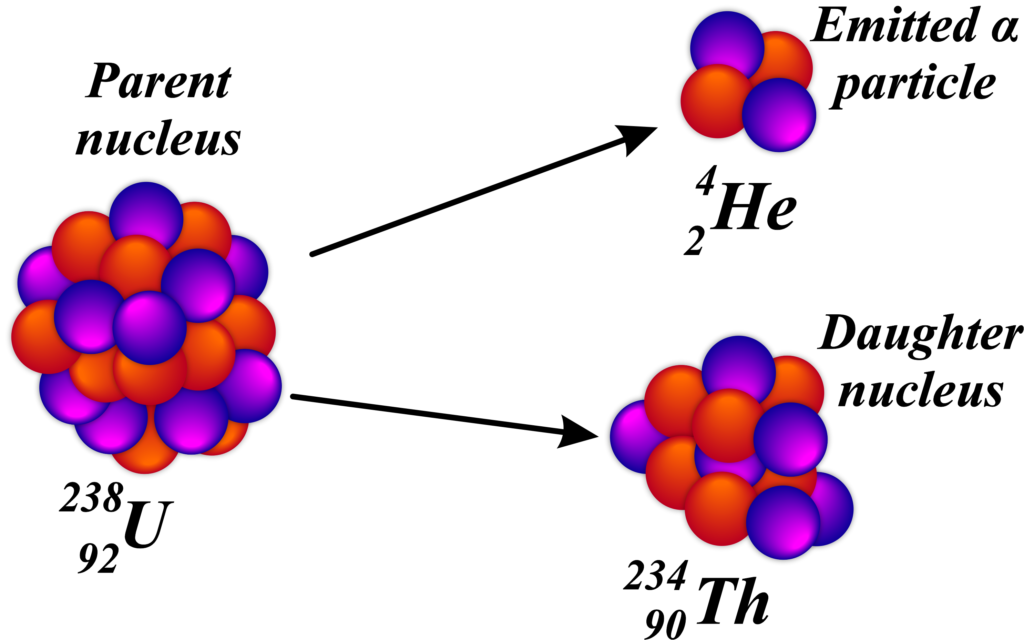
When an alpha particle leaves the nucleus, the original atom changes into a new element because it loses two protons. The atomic number (which tells us what element it is) goes down by two, and the mass number (the total number of protons and neutrons) goes down by four.

Here’s a simple equation that represents alpha decay:

\(\displaystyle {Z}^{A}\text{X} \rightarrow {Z-2}^{A-4}\text{Y} + _{2}^{4}\text{He}\)

In this equation:

• (\(\displaystyle _{Z}^{A}\text{X} \)) is the original unstable nucleus (the ‘crowded bus’).
• (\(\displaystyle _{Z-2}^{A-4}\text{Y} \)) is the new nucleus formed after the decay (the ‘bus’ after a few people got off).
• (\(\displaystyle _{2}^{4}\text{He} \)) is the alpha particle that’s emitted (the ‘people’ who got off the bus).

An example of alpha decay is the transformation of uranium into thorium:

\(\displaystyle {92}^{238}\text{U} \rightarrow {90}^{234}\text{Th} + _{2}^{4}\text{He}\)

In this example, uranium-238 loses an alpha particle and becomes thorium-234. Alpha decay helps heavy, unstable nuclei become more stable by releasing an alpha particle, which is like a tiny helium nucleus. It’s one-way nature tries to balance things out and make them more comfortable, just like passengers getting off a crowded bus.

Nuclear Stability and Alpha Decay:

The process of alpha decay is intimately related to the concept of nuclear stability. The stability of a nucleus depends on the balance between two forces: the strong nuclear force and the electromagnetic force. The strong nuclear force is a powerful, attractive force that acts between all nucleons (protons and neutrons) and is what holds the nucleus together. On the other hand, the electromagnetic force causes repulsion between the positively charged protons.

For lighter nuclei, the strong nuclear force easily overcomes the repulsion between protons, leading to a stable nucleus. However, as nuclei get larger, the number of protons increases, and so does the repulsive electromagnetic force. If the nucleus becomes too large, the strong nuclear force can barely counterbalance the electromagnetic repulsion, leading to instability.

Alpha decay is a way for a heavy, unstable nucleus to increase its stability. By emitting an alpha particle, which consists of two protons and two neutrons, the nucleus reduces its size and the repulsive force between the remaining protons. This results in a new nucleus that is closer to the line of stability—a region in the chart of nuclides where nuclei are stable.

For example, a nucleus with 210 or more nucleons is so large that the strong nuclear force holding it together can just barely counterbalance the electromagnetic repulsion between the protons it contains. Alpha decay occurs in such nuclei as a means of increasing stability by reducing size.

Alpha decay is a natural process that heavy, unstable nuclei undergo to achieve greater stability. It’s a balancing act where the nucleus sheds some of its mass and charge to reach a more stable, energetically favorable state.

Beta Decay

Beta decay is a type of radioactive decay where a nucleus transforms by emitting a beta particle, which can be either an electron or a positron. In the nucleus of an atom, we have protons, which are positively charged, and neutrons, which have no charge. The number of these particles determines the identity and stability of the atom. Sometimes, a nucleus has either too many protons or too many neutrons to be stable. To reach a more stable state, it can undergo beta decay.

\(\displaystyle ^{14}_{6}C \rightarrow ^{14}_{7}N + e^- \)

There are two types of beta decay:

Beta-minus (β−) decay: Beta-minus (β−) decay happens when a neutron in the nucleus turns into a proton and emits an electron (the beta particle) along with an antineutrino. The antineutrino is a nearly massless particle that carries away some energy but doesn’t interact much with matter. The equation for beta-minus decay become,

\(\displaystyle {Z}^{A}\text{X} \rightarrow {Z+1}^{A}\text{Y} + e^{-} + \bar{\nu}_e\)

Here, (\(\displaystyle {Z}^{A}\text{X} \)) is the original nucleus, (\(\displaystyle {Z+1}^{A}\text{Y} \)) is the new nucleus with one more proton, (e^–) is the emitted electron, and (\(\displaystyle\bar{\nu}_e\)) is the antineutrino.

Beta-plus (β+) decay: In this process, a proton is converted into a neutron, and the nucleus emits a positron (the antimatter counterpart of the electron) and a neutrino. This type of decay occurs in proton-rich nuclei. The equation for beta-plus decay is

\(\displaystyle {Z}^{A}\text{X} \rightarrow {Z-1}^{A}\text{Y} + e^{+} + \nu_e\)

Where (\(\displaystyle {Z}^{A}\text{X} \)) is the original nucleus, (\(\displaystyle {Z-1}^{A}\text{Y} \)) is the new nucleus with one less proton, (e⁺}) is the emitted positron, and (\(\displaystyle \nu_e \)) is the neutrino.

In both beta decay types, the nucleus’s mass number (denoted by (A) stays the same because a proton and a neutron have almost the same mass. However, the atomic number (denoted by (Z) changes by one unit, meaning the element changes to a new element in the periodic table. Beta decay is a way for an atom to move closer to the optimal ratio of neutrons to protons, which increases its stability. It’s a natural process that helps balance the forces within the nucleus.

Gamma Decay

Involves the emission of gamma rays from the nucleus, usually following alpha or beta decay to get rid of excess energy. Imagine you’re at a party and you’ve just danced an energetic dance. You’re feeling pretty excited and full of energy. Now, to relax, you take a deep breath and let out a sigh of relief. In a way, gamma decay is like that sigh—it’s how an excited nucleus releases excess energy to return to a calmer, more stable state.

When a nucleus undergoes alpha or beta decay, it often ends up in an excited state with extra energy. This is because the particles it emits carry away some, but not all, of the energy from the nucleus. The nucleus is left with more energy than it needs to be stable.

To get rid of this extra energy, the nucleus emits a gamma ray, which is a very high-energy photon. Photons are particles of light, and gamma rays are the most energetic form of light. They don’t have any mass or charge, so they’re just pure energy.

The process doesn’t change the number of protons or neutrons in the nucleus, so the element remains the same. What changes is the energy level of the nucleus—it drops from a higher, excited state to a lower, more stable one.

Here’s a simple way to represent gamma decay:

\(\displaystyle {Z}^{A}\text{X}^* \rightarrow {Z}^{A}\text{X} + \gamma\)

In this equation:

• (\(\displaystyle _{Z}^{A}\text{X}^* \)) is the excited nucleus.
• (\(\displaystyle _{Z}^{A}\text{X} \)) is the nucleus in its lower energy state.
• (γ) is the gamma-ray emitted.

Gamma decay is the nucleus’s way of going from a high-energy state to a lower-energy state by emitting a gamma ray.

Difference between Gamma, Beta & Alpha Decay

Type of Decay	Alpha Decay (α-decay)	Beta Decay (β-decay)	Gamma Decay (γ-decay)
Particle Emitted	Alpha particle (2 protons and 2 neutrons)	Beta particle (electron or positron)	The nucleus emits a helium nucleus
Mass Number Change	Decreases by 4	Remains the same	Remains the same
Atomic Number Change	Decreases by 2	Increases by 1 (β− decay) or decreases by 1 (β+ decay)	Remains the same
Penetrating Power	Low (stopped by paper)	Moderate (stopped by metal foils)	High (can penetrate thick lead)
Ionizing Power	High (strongly ionizing due to size and charge)	Moderate (ionizing due to charge)	Low (ionizing due to energy)
Shielding Required	Paper or skin	Metal foil	Thick lead or concrete
Nature of Emission	Nucleus emits a helium nucleus	Nucleus emits an electron or positron	Nucleus emits energy without changing its composition
Example	Uranium-238 decaying to Thorium-234	Carbon-14 decaying to Nitrogen-14 (β− decay)	Excited Cobalt-60 nucleus releasing energy

This table outlines the key differences between the three types of decay, focusing on what is emitted, how the nucleus changes, and the properties of each type of radiation. It’s important to note that while alpha and beta decay results in the transformation of one element into another, gamma decay involves only the release of energy, leaving the element itself unchanged.

Uses of Radioactivity

Radioactivity has many uses, such as in medicine for cancer treatment, in archaeology for carbon dating, and power generation in nuclear reactors. Here are some key uses of radioactivity:

• Medical Diagnosis and Treatment: Radioactive isotopes are used in medical imaging techniques like PET scans to diagnose conditions. They’re also used in radiotherapy to treat cancer by targeting and destroying cancerous cells.
• Sterilization: Gamma rays from radioactive materials can sterilize medical equipment and food by killing bacteria and other pathogens without raising the temperature.
• Smoke Detectors: Americium-241, a radioactive element, is used in many smoke detectors. It ionizes the air, making it conductive; when smoke disrupts this conductivity, the alarm is triggered.
• Energy Production: Radioactive elements like uranium and plutonium are used as fuel in nuclear reactors to produce electricity.
• Food Preservation: Similar to sterilization, gamma radiation can be used to kill bacteria, parasites, and other organisms in food, extending its shelf life.
• Agriculture: Radioactive isotopes can be used to create mutations in seeds, leading to new plant varieties with desirable traits.
• Archaeology and Geology: Carbon-14 dating is a well-known application of radioactivity, used to determine the age of archaeological finds. Other isotopes are used to date rocks and understand geological processes.

These are just a few examples of how radioactivity is utilized in our world. Each application takes advantage of the unique properties of radioactive decay to serve a beneficial purpose.

Advantages and Disadvantages of Radioactivity

Radioactivity, while a natural phenomenon, has both advantages and disadvantages when harnessed for human use.

Advantages of Radioactivity:

• Medical Treatments: Radioactive isotopes are used in radiotherapy to target and destroy cancer cells. For example, Cobalt-60 is used to treat certain types of cancer.
• Diagnostic Imaging: Gamma rays are used in medical imaging techniques like PET scans to visualize internal parts of the body.
• Food Preservation: Gamma radiation can kill microbes in food, extending its shelf life and preventing decay.
• Sterilization: Radioactivity can sterilize medical instruments without the need for heat, which can damage delicate equipment.
• Agricultural Improvements: Radiation can induce mutations in seeds, leading to new plant varieties with beneficial traits.

Disadvantages of Radioactivity:

• Health Risks: Exposure to high levels of radiation can cause radiation sickness, cancer, and genetic damage.
• Environmental Impact: Radioactive waste can contaminate the environment if not properly managed.
• Security Concerns: Radioactive materials can be dangerous if used in malicious ways, such as in nuclear weapons or dirty bombs.
• Accidents: Nuclear accidents, while rare, can have devastating and long-lasting effects on people and the environment.

Also Read: Atomic Mass and Composition of Nucleus

Solved Examples

Problem 1: A sample of a radioactive isotope has an initial activity of 4000 Bq. After 3 hours, the activity drops to 500 Bq. Calculate the half-life of the isotope.

Solution: The activity (A) at any time (t ) is given by:

\(\displaystyle A = A_0 e^{-\lambda t} \)

Given:

\(\displaystyle A_0 = 4000 \, \text{Bq} \)

\(\displaystyle A = 500 \, \text{Bq} \)

\(\displaystyle t = 3 \, \text{hours} \)

First, we find the decay constant (λ):

\(\displaystyle \frac{A}{A_0} = e^{-\lambda t} \)

\(\displaystyle \frac{500}{4000} = e^{-\lambda \times 3} \)

\(\displaystyle \frac{1}{8} = e^{-3\lambda} \)

Taking the natural logarithm on both sides:

\(\displaystyle \ln \left(\frac{1}{8}\right) = -3\lambda \)

\(\displaystyle -\ln(8) = -3\lambda \)

\(\displaystyle \lambda = \frac{\ln(8)}{3} \)

\(\displaystyle \lambda = \frac{2.079}{3} \)

\(\displaystyle \lambda = 0.693 \, \text{hr}^{-1} \)

The half-life (T_1/2) is related to the decay constant (λ) by:

\(\displaystyle T_{1/2} = \frac{\ln(2)}{\lambda} \)

\(\displaystyle T_{1/2} = \frac{0.693}{0.693} \)

\(\displaystyle T_{1/2} = 1 \, \text{hour} \)

The half-life of the isotope is 1 hour.

Problem 2: Calculate the energy released in the alpha decay of (\(\displaystyle ^{238}_{92} \text{U} \)) to (\(\displaystyle ^{234}_{90} \text{Th} \)). The masses are: (\(\displaystyle ^{238}_{92} \text{U} = 238.05078 \, \text{u} \)), (\(\displaystyle ^{234}_{90} \text{Th} = 234.04363 \, \text{u} \)), and (\(\displaystyle ^{4}_{2} \text{He} = 4.00260 \, \text{u} \)).

Solution: The energy released (Q) in alpha decay is given by the mass defect converted to energy:

\(\displaystyle Q = \left( m_{\text{parent}} – m_{\text{daughter}} – m_{\alpha} \right) c^2 \)

Given:

\(\displaystyle m_{\text{parent}} = 238.05078 \, \text{u} \)

\(\displaystyle m_{\text{daughter}} = 234.04363 \, \text{u} \)

\(\displaystyle m_{\alpha} = 4.00260 \, \text{u} \)

Calculate the mass defect:

\(\displaystyle \Delta m = m_{\text{parent}} – (m_{\text{daughter}} + m_{\alpha}) \)

\(\displaystyle \Delta m = 238.05078 – (234.04363 + 4.00260) \)

\(\displaystyle \Delta m = 238.05078 – 238.04623 \)

\(\displaystyle \Delta m = 0.00455 \, \text{u} \)

Convert the mass defect to energy (1 u = 931 MeV/c²):

\(\displaystyle Q = \Delta m \times 931 \, \text{MeV/u} \)

\(\displaystyle Q = 0.00455 \times 931 \)

\(\displaystyle Q = 4.24 \, \text{MeV} \)

The energy released in the alpha decay of (\(\displaystyle ^{238}_{92} \text{U} \)) is 4.24 MeV.

Problem 3: In a beta decay experiment, the kinetic energy of the emitted beta particle (electron) is found to be 0.782 MeV. If the mass of the parent nucleus is 39.963998 u and the mass of the daughter nucleus is 39.962590 u, calculate the mass of the neutrino assuming it to be nearly massless.

Solution: The energy released (Q) in beta decay is given by:

\(\displaystyle Q = (m_{\text{parent}} – m_{\text{daughter}}) c^2 \)

Given:

\(\displaystyle m_{\text{parent}} = 39.963998 \, \text{u} \)

\(\displaystyle m_{\text{daughter}} = 39.962590 \, \text{u} \)

Calculate the mass defect:

\(\displaystyle \Delta m = m_{\text{parent}} – m_{\text{daughter}} \)

\(\displaystyle \Delta m = 39.963998 – 39.962590 \)

\(\displaystyle \Delta m = 0.001408 \, \text{u} \)

Convert the mass defect to energy (1 u = 931 MeV/c²):

\(\displaystyle Q = \Delta m \times 931 \, \text{MeV/u} \)

\(\displaystyle Q = 0.001408 \times 931 \)

\(\displaystyle Q = 1.31 \, \text{MeV} \)

The energy is shared between the electron and the neutrino. Given the kinetic energy of the electron:

\(\displaystyle E_{\beta} = 0.782 \, \text{MeV} \)

The energy of the neutrino (E_ν) is:

\(\displaystyle E_{\nu} = Q – E_{\beta} \)

\(\displaystyle E_{\nu} = 1.31 – 0.782 \)

\(\displaystyle E_{\nu} = 0.528 \, \text{MeV} \)

Assuming the neutrino is massless, its energy is equivalent to its momentum, thus confirming the given assumption. The mass of the neutrino is nearly massless, and the energy released in the beta decay is shared as 0.782 MeV for the electron and 0.528 MeV for the neutrino.

Problem 4: A nucleus in an excited state decays to its ground state by emitting a gamma photon of energy 1.25 MeV. If the excited state had an energy of 2.50 MeV, what is the energy of the ground state?

Solution: The energy of the ground state (E_ground) is given by:

\(\displaystyle E_{\text{ground}} = E_{\text{excited}} – E_{\gamma} \)

Given:

\(\displaystyle E_{\text{excited}} = 2.50 \, \text{MeV} \)

\(\displaystyle E_{\gamma} = 1.25 \, \text{MeV} \)

Calculate the energy of the ground state:

\(\displaystyle E_{\text{ground}} = 2.50 \, \text{MeV} – 1.25 \, \text{MeV} \)

\(\displaystyle E_{\text{ground}} = 1.25 \, \text{MeV} \)

The energy of the ground state is 1.25 MeV.

Problem 5: A sample of a radioactive substance contains (10²⁰) nuclei. The half-life of the substance is 2 hours. How many nuclei remain after 6 hours?

Solution: The number of remaining nuclei (N) after time (t) is given by:

\(\displaystyle N = N_0 \left( \frac{1}{2} \right)^{\frac{t}{T_{1/2}}} \)

Given:

\(\displaystyle N_0 = 10^{20} \)

\(\displaystyle T_{1/2} = 2 \, \text{hours} \)

\(\displaystyle t = 6 \, \text{hours} \)

Calculate the number of half-lives:

\(\displaystyle \frac{t}{T_{1/2}} = \frac{6}{2} = 3 \)

Calculate the remaining nuclei:

\(\displaystyle N = 10^{20} \left( \frac{1}{2} \right)^3 \)

\(\displaystyle N = 10^{20} \times \frac{1}{8} \)

\(\displaystyle N = 1.25 \times 10^{19} \)

After 6 hours, (\(\displaystyle 1.25 \times 10^{19}\)) nuclei remain.

Problem 6: A person is exposed to a radioactive source that emits gamma rays with an activity of 2000 Bq. If the exposure lasts for 5 hours and the energy absorbed per decay is (\(\displaystyle1.5 \times 10^{-13} \, \text{J}\)), calculate the total energy absorbed.

Solution: The total number of decays (N) is given by:

\(\displaystyle N = A \times t \)

Given:

\(\displaystyle A = 2000 \, \text{Bq} \)

\(\displaystyle t = 5 \, \text{hours} = 5 \times 3600 \, \text{s} = 18000\, \text{s} \)

Calculate the total number of decays:

\(\displaystyle N = 2000 \times 18000 \)

\(\displaystyle N = 3.6 \times 10^7 \)

The total energy absorbed (E) is given by:

\(\displaystyle E = N \times \text{energy per decay} \)

Given:

\(\displaystyle \text{energy per decay} = 1.5 \times 10^{-13} \, \text{J} \)

Calculate the total energy absorbed:

\(\displaystyle E = 3.6 \times 10^7 \times 1.5 \times 10^{-13} \)

\(\displaystyle E = 5.4 \times 10^{-6} \, \text{J} \)

The total energy absorbed by the person is (\(\displaystyle 5.4 \times 10^{-6} \)) J.

FAQs