The understanding of light and its refraction has evolved over centuries. Imagine a time when the mysteries of light were as vast as the night sky. Our story begins in ancient Greece, around 800 BC, where the earliest recorded thoughts on light and vision were penned. The Greeks, with their insatiable curiosity, laid the groundwork for optical science.
After the Greek era, there was a lull in significant advancements until around 750 AD. This is when the Islamic civilization, with centers in Baghdad and Cordoba, took the baton of scientific inquiry. They not only preserved Greek knowledge but also expanded upon it, leading to a golden age of learning that lasted until the late 13th century.
Fast forward to the early 1600s, a Dutch mathematician named Willebrord Snell made a groundbreaking discovery. He found that the bending of light, or refraction, followed a specific law, which we now know as Snell’s Law. Although Snell discovered this law, it was the French philosopher René Descartes who first published the formulation we use today.
The understanding of refraction has had profound implications. It led to the development of lenses, telescopes, and a deeper understanding of how we see the world. Galileo, for instance, used his knowledge of refraction to improve the design of the telescope, leading to his discovery of Jupiter’s moons and Saturn’s rings.
What is the Refraction of Light?
Refraction of light is the bending of light rays when they pass from one medium to another with a different density. This bending occurs because light travels at different speeds in different materials. To understand this, let’s imagine light as a group of travelers walking from a concrete path onto a sandy beach. On the hard concrete, they can walk quickly, but as soon as they step onto the sand, their speed decreases because it’s harder to walk on. This change in speed causes them to change direction slightly.
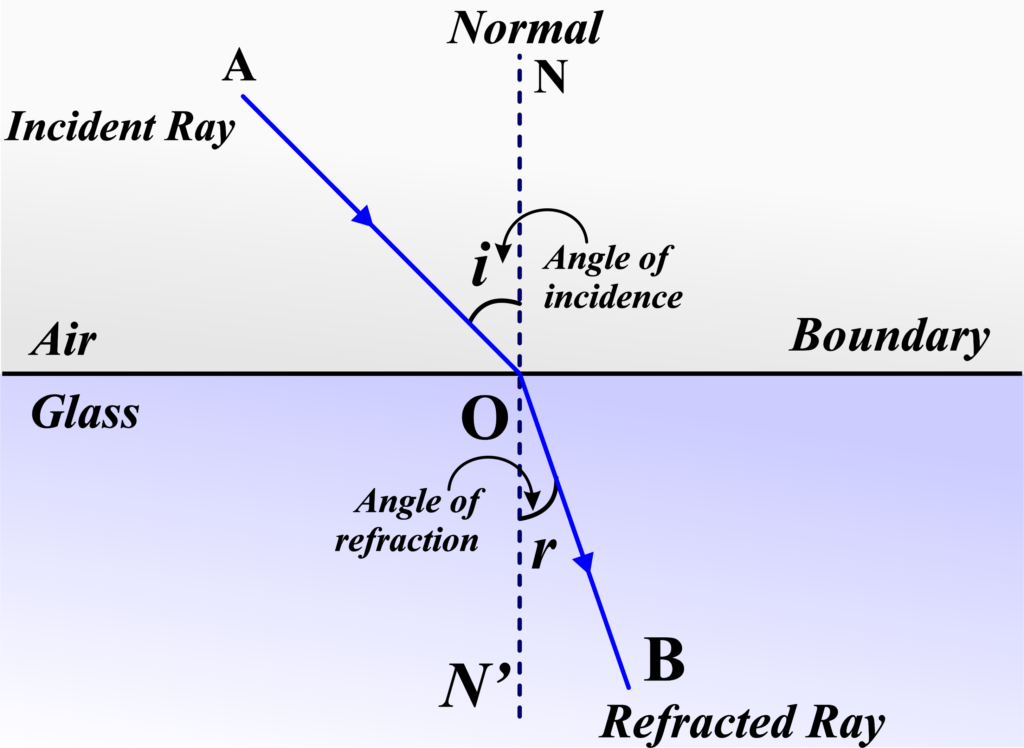
In the world of physics, when light moves from a medium like air (where it travels fast) into a medium like water or glass (where it travels slower), it bends towards an imaginary line called the normal. This bending is what we call refraction. It happens because light travels at different speeds in different materials. The speed of light is fastest in a vacuum, like space, and it slows down when it passes through anything else, like air, water, or glass.
Now, why does light bend? It’s all about the wave nature of light. Light behaves like a wave, and just like a water wave bends around a rock or changes direction when it hits the shore at an angle, light waves bend when they hit a new medium at an angle.
This bending of light has some interesting consequences. For example, it’s why a straw in a glass of water looks bent at the surface or why pools look shallower than they are. It’s also why lenses can focus light, which is crucial for things like eyeglasses and cameras.
Example: A classic example of a straw in a glass of water to understand the refraction of light. When you place a straight straw into a glass of water, you might notice that the straw appears to be bent at the point where the air and water meet. This is a perfect illustration of light refraction.

Here’s what’s happening: Light travels through various mediums at different speeds. In the air, light travels relatively fast. When it hits the water, which is denser than air, it slows down. This change in speed as light enters a new medium causes it to change direction, a process known as refraction.
Now, imagine light rays coming from the part of the straw that’s submerged in water. As these rays exit the water and enter the air, they speed up and bend away from the normal line (an imaginary line perpendicular to the surface).
To our eyes, these rays appear to come from a higher position than they do. Our brain interprets this information and we see the straw as bent.
This bending is not random; it follows precise laws. The degree to which the light bends depends on the angle at which it hits the water’s surface and the refractive indices of the air and water. The refractive index is a measure of how much a medium can bend light.
The straw looks bent because of the refraction of light. This phenomenon is a fundamental concept in physics that explains how light behaves when transitioning between mediums with different densities. It’s the same principle that allows lenses to focus light and our eyes to form images, making it a cornerstone of optical science. So, in essence, refraction is the bending of light due to a change in its speed as it passes from one medium to another.
Terminology used in refraction: Understanding the terminology used in refraction is like learning the language of light’s behavior as it travels through different mediums.
- Normal: Think of this as an imaginary straight line that stands upright, perpendicular to the boundary where the light ray meets a new medium. It’s like a flagpole standing on the border between two countries.
- Incident Ray: This is the light ray that arrives and strikes the boundary between two mediums. Imagine it as a traveler reaching the border checkpoint.
- Refracted Ray: After the incident ray hits the boundary and enters the new medium, it becomes the refracted ray. It’s like the traveler continuing their journey but on a different path due to the rules of the new country.
- The angle of Incidence: The angle between the incident ray and the normal. It’s measured from the normal to the path of the incoming light ray, like measuring how far a door has been opened from its closed position.
- The angle of Refraction: The angle between the refracted ray and the normal. This is measured from the normal to the path of the bent light ray, showing how much the light has ‘turned’ inside the new medium.
- Refractive Index: A number that describes how much a material can bend light. It’s like a rating for each medium that tells us how much it can slow down and bend the light passing through it.
These terms form the basic vocabulary when discussing refraction. They help us describe and predict how light behaves when it moves from one medium to another, which is essential for understanding optical phenomena and solving related problems in physics.
Causes of Refraction
The cause of refraction is the change in the speed of light as it passes from one medium to another, which is influenced by the optical density of the materials and the angle at which light enters the new medium. To understand the causes of refraction, let’s think about light as if it were a car traveling from a paved road onto a gravel path. When the car is on a smooth road, it can go fast, but as soon as it hits the gravel, it slows down and its path might change slightly. This is similar to what happens to light during refraction.
The Speed Change:
The primary cause of refraction is the change in the speed of light as it moves from one medium to another. Light travels at different speeds in different materials. For example, it moves faster in air and slower in water or glass. When light rays enter a new medium at an angle, they slow down or speed up, depending on the optical density of the medium.
Optical Density:
Optical density is a measure of how much a material can slow down light. A medium like glass, which is optically denser than air, will slow down the light more than air does. This slowing down of light as it enters a denser medium is what causes the light to bend or refract.
The Bending:
The bending of light, or refraction, occurs because the part of the light wave that enters the new medium first slows down before the rest of the wave. This causes the light wave to change direction. It’s like a marching band turning a corner; the person on the inside of the turn slows down, causing the line to pivot and change direction.
The Angle of Entry:
The angle at which light enters a new medium also affects refraction. If light hits the new medium straight on (perpendicular to the surface), it will slow down but won’t change direction. However, if it enters at an angle, the change in speed will cause the light to bend.
Laws of Refraction of Light
There are two laws of refraction:
First Law of Refraction
The first law of refraction, often referred to as the law of planarity, is a fundamental concept in the study of light behavior. It states that the incident ray (the incoming light), the refracted ray (the outgoing light), and the normal (an imaginary line perpendicular to the surface at the point of incidence) all lie in the same plane.
Example: Refraction through a Rectangular Glass Slab
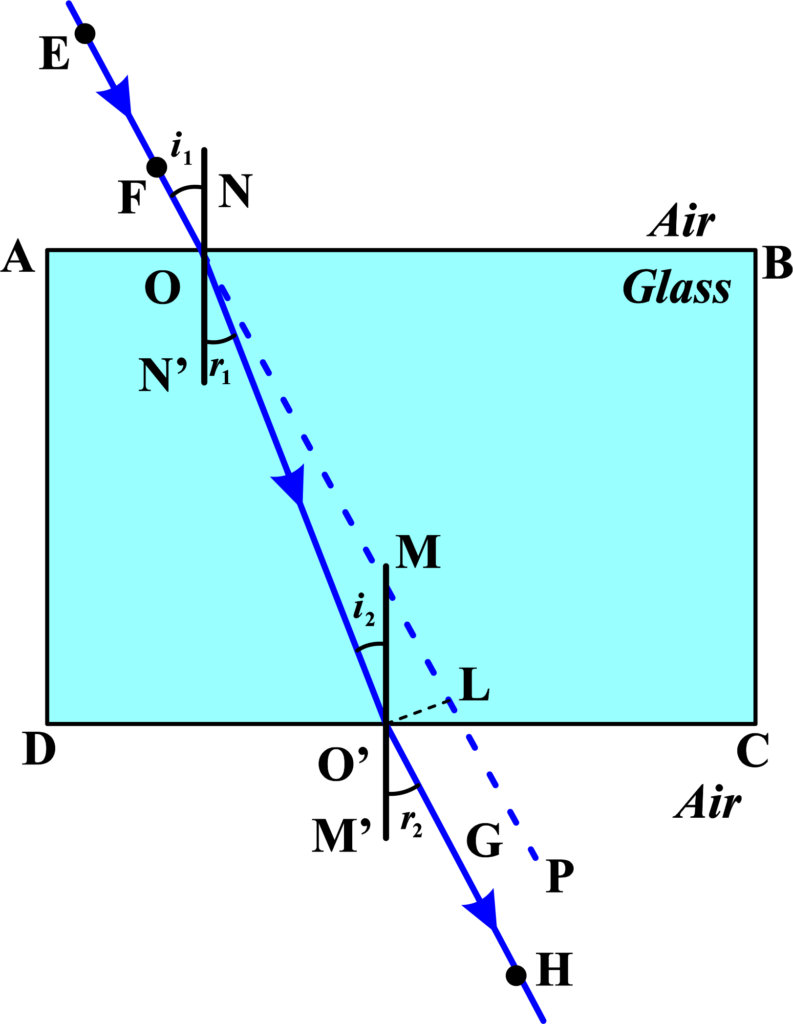
Imagine experimenting with a rectangular glass slab placed on a piece of paper. You outline the slab and mark its sides as ABCD. Now, you place two pins, say E and F, at the edge of side AB. When you look at the images of these pins through the opposite side of the slab, you place two more pins, G and H, such that they align with the images of E and F when viewed from the side CD.
After removing the pins and the slab, you join the points E and F and extend the line to meet AB at point O. Similarly, you join G and H and extend it to meet CD.
What you’ll notice is that the lines EF and GH, although they represent the path of light entering and exiting the slab (incident and refracted rays), and the normal line you would draw at point O, all lie in the same plane. This is a practical demonstration of the first law of refraction.
Snell’s Law
Snell’s Law is a principle that describes how light bends, or refracts, as it travels through different materials. It’s named after the Dutch mathematician Willebrord Snellius who discovered the law in 1621. The second law of refraction (Snell’s Law) tells us about the relationship between the angles of incidence and refraction and the mediums’ refractive indices. It states that the ratio of the sine of the angle of incidence to the sine of the angle of refraction is constant for a given pair of media.
Imagine you’re playing a game where you have to run from one point to another, but halfway through, you have to run through a pool of water. You’d notice that as soon as you hit the water, you slow down and your path shifts slightly. This change in speed and direction is similar to what happens to light when it passes from air into water.
Snell’s Law can be expressed with a simple formula:
\(\displaystyle\begin{equation}\label{eqn:1}\boxed{\boldsymbol{n_{1} \sin(\theta_{1}) = n_{2} \sin(\theta_{2}) }} \end{equation}\)
Here’s what each part of the formula represents:
- (n1) and (n2) are the refractive indices of the first and second medium, respectively. These numbers tell us how much the medium can bend light.
- (θ1) is the angle of incidence, which is the angle between the incoming light ray and an imaginary line called the normal.
- (θ2) is the angle of refraction, which is the angle between the refracted ray and the normal.
What Snell’s Law is saying is that the product of the refractive index and the sine of the angle of incidence for the first medium is equal to the product of the refractive index and the sine of the angle of refraction for the second medium.
Example: Light Entering Water
Let’s consider a scientific example where light travels from air into water. We know that air has a refractive index of approximately 1 (since it’s very close to a vacuum), and water has a refractive index of about 1.33.
When a ray of light from the air hits the water surface at an angle, it bends towards the normal—line perpendicular to the surface. According to Snell’s Law, the sine of the angle of incidence (in air) divided by the sine of the angle of refraction (in water) will equal the ratio of the refractive indices of water to air.
Mathematically, we can express this as:
\(\displaystyle\begin{equation}\label{eqn:2}\boxed{\boldsymbol{\frac{\sin(\theta_{\text{air}})}{\sin(\theta_{\text{water}})} = \frac{n_{\text{water}}}{n_{\text{air}}} }} \end{equation}\)
If we plug in the refractive indices, we get:
\(\displaystyle\frac{\sin(\theta_{\text{air}})}{\sin(\theta_{\text{water}})} = \frac{1.33}{1} \)
This equation allows us to calculate the angle of refraction if we know the angle of incidence and vice versa. It’s a powerful tool in optics that helps us understand and predict how light will behave when it encounters different materials.
Snell’s Law provides a mathematical way to quantify the bending of light, which is crucial for designing lenses, glasses, and various optical instruments.
What is the Refractive Index?
The refractive index is the ratio of the speed of light in a vacuum to its speed in a medium. It indicates how much the light will bend in that medium. It’s a number without any units, like a score, that compares the speed of light in a vacuum to its speed in the material. Here’s a simple way to understand it:
- In a vacuum, where there’s absolutely nothing to slow it down, light travels at its fastest speed.
- When light enters any other material, like air, water, or glass, it slows down a bit because these materials are denser than a vacuum.
The refractive index (usually represented by the letter n) tells us exactly how much slower the light travels in the material compared to a vacuum. The formula for calculating the refractive index is:
\(\displaystyle\begin{equation}\label{eqn:3}\boxed{\boldsymbol{n = \frac{c}{v} }} \end{equation}\)
- c is the speed of light in a vacuum (the fastest possible speed for light).
- v is the speed of light in the material (which is always slower than c).
If the refractive index is greater than 1, it means light slows down in that material. The higher the refractive index, the more the light slows down and the more it bends. This number is crucial for understanding how light interacts with materials and is used in many areas of physics and engineering. It’s like a “fingerprint” for every material that tells us about its optical properties.
Example: Light from Air to Water
Let’s say we have a light ray moving from air into water. We know that light in the air has a speed of about 300,000 kilometers per second. When it enters water, it slows down because water is denser than air. The refractive index of water is 1.33, which means light in water travels at ( \(\displaystyle\frac{1}{1.33}\)) or about 75% of its speed in air. The refractive index (n) ends up being greater than 1 for water. This number, 1.33 for water, helps us predict how much light will bend when it enters from air to water.
Types of Refraction
Refraction is the bending of light as it passes from one medium to another, and it can occur in various forms. Refraction can be natural, like atmospheric refraction causing mirages, or artificial, like the bending of light through lenses.
Natural Refraction
Natural refraction occurs in nature, like the bending of light in the atmosphere, which causes phenomena such as the twinkling of stars or the formation of mirages. Natural refraction is a type of refraction that occurs in the environment around us, without any human-made tools or devices. It’s all about how light bends when it passes through different natural substances, like air, water, or the atmosphere.
When light travels through the air and enters another medium like water or the atmosphere, it changes speed because these mediums have different densities. This change in speed causes the light to bend. This bending of light is what we call refraction.
In nature, this happens all the time and leads to some beautiful and intriguing phenomena. For example, the twinkling of stars is caused by the refraction of starlight as it passes through the Earth’s atmosphere, which has layers of air with varying densities. Another example is a mirage, an optical illusion that makes it look like there’s water on the road on a hot day. This happens because the light from the sky bends as it passes through layers of hot and cooler air.
So, natural refraction is the bending of light that occurs when it moves through different natural mediums, and it’s responsible for many of the visual effects we see in our daily lives.
Artificial Refraction
Artificial refraction happens when light passes through man-made objects like lenses, prisms, or glass windows. It’s the type of refraction we harness in optical devices.
Artificial refraction refers to the bending of light that occurs due to human-made structures or devices, such as lenses, prisms, and glasses. Unlike natural refraction, which happens in nature, artificial refraction is designed and utilized for specific purposes.
When light passes through specially crafted objects like a lens in a pair of spectacles, it bends in a controlled way. This bending is due to the shape of the lens and the material it’s made from, both of which are chosen to direct the light precisely where it’s needed. For example, in eyeglasses, lenses are shaped to correct vision by focusing light onto the retina in just the right way.
In artificial refraction, we’re essentially guiding light along a path we’ve determined to achieve a desired effect, whether it’s to help someone see better, to magnify an image, or to split light into a spectrum of colors with a prism. It’s a type of refraction that showcases human ingenuity in manipulating light for our benefit.
Refraction from Denser to Rarer Medium
When light moves from a denser medium, like water, to a rarer medium, like air, it bends away from the normal. This is why objects underwater appear shifted when viewed from above.
Imagine light as a group of runners on a track. These runners are moving from a section of the track made of thick mud (the denser medium) to a section made of firm ground (the rarer medium). In the mud, their speed is slower because it’s harder to run. As soon as they step onto the firm ground, they can speed up. The runners who hit the firm ground first will speed up sooner, causing the whole group to bend away from their original path. This change in direction is similar to how light refracts when it goes from a denser medium, like glass, into a rarer medium, like air.
In physics terms, when light exits a material like water or glass and enters air, it speeds up and bends away from the normal—the imaginary line perpendicular to the surface at the point where the light exits. This is why objects submerged in water appear to be at a different depth when viewed from above; the light rays coming from the object bend away from the normal as they enter the air, changing the apparent position of the object.
Refraction from Rarer to Denser Medium
Conversely, when light goes from a rarer medium to a denser one, it bends towards the normal. This bending is what allows lenses to focus light and is essential in the functioning of our eyes. To understand this, let’s consider light as a group of people walking side by side. These people represent a wavefront of light.
Now, imagine these people walking from a flat field (rarer medium) into a forest (denser medium). As they enter the forest, their speed decreases because it’s harder to walk among trees than on an open field. The people who enter the forest first will slow down sooner, causing the group to pivot towards the point of entry. This pivot is similar to how light bends towards the normal—an imaginary line perpendicular to the boundary between two mediums—when it moves from a rarer medium, like air, into a denser medium, like water or glass.
In physics terms, when light enters a denser medium, it slows down due to the increased optical density, and this change in speed causes the light to bend towards the normal.
Characteristics of Refraction
When we talk about the characteristics of refraction, we’re looking at the specific ways light behaves when it passes from one medium into another. Here are the key characteristics
- Frequency Remains Constant: The frequency of light, which determines its color, does not change during refraction. No matter how much the light bends, the color you see remains the same.
- Velocity and Wavelength Change: While the frequency stays the same, the speed (velocity) of light and its wavelength do change when light refracts. If light enters a denser medium, it slows down, and its wavelength gets shorter.
- Direction Changes: The most noticeable characteristic of refraction is the change in direction of the light ray. When light moves from one medium to another with a different refractive index, it bends. This bending is what we call refraction.
Also Read: Reflection of Light by Spherical Mirrors
Applications of Refraction of Light
Refraction of light, the bending of light as it passes from one medium to another, has numerous applications that are integral to our daily lives.
- Vision Correction: Spectacles and contact lenses use refraction to correct vision. They adjust the path of light to focus it properly on the retina, helping to correct nearsightedness or farsightedness.
- Optical Instruments: Microscopes and telescopes rely on lenses that refract light to magnify images of tiny or distant objects, allowing us to see details that would otherwise be invisible to the naked eye.
- Cameras: In cameras, lenses refract light to focus images onto film or a digital sensor, capturing them as photographs. The ability to adjust focus is a direct application of the principles of refraction.
- Projectors: Movie projectors use lenses to refract light, projecting magnified images onto screens. This principle is also used in slide projectors and overhead projectors in classrooms.
- Peepholes: The peepholes in doors use a special convex lens to refract light in a way that allows you to see a wide angle of the area outside your door from a small aperture.
- Eyeglasses for Presbyopia: Bifocals and progressive lenses are designed to help people with presbyopia, a condition that affects the ability to focus on close objects. These glasses use refraction to provide different levels of magnification for different viewing distances.
- Safety on Roads: The reflective coating on road signs and the paint used for lane markers often contain tiny glass beads that refract light from car headlights, making them more visible at night.
- Medical Devices: Instruments like endoscopes use the principles of refraction to allow doctors to see inside the human body without invasive surgery.
Solved Examples
Example 1: A light ray passes from air (refractive index = 1.0) into water (refractive index = 1.33). If the angle of incidence in air is 30°, calculate the angle of refraction in water.
Solution: We use Snell’s Law
\(\displaystyle n_1 \sin \theta_1 = n_2 \sin \theta_2\)
Given: n1 = 1.0 (air); n2 = 1.33 (water); (θ1 = 30∘)
Substitute the values:
\(\displaystyle 1.0 \sin 30^\circ = 1.33 \sin \theta_2\)
Since (\(\displaystyle\sin 30^\circ = 0.5\)):
\(\displaystyle 0.5 = 1.33 \sin \theta_2\)
\(\displaystyle\sin \theta_2 = \frac{0.5}{1.33} \approx 0.376\)
Now find (θ2):
\(\displaystyle\theta_2 = \sin^{-1}(0.376) \approx 22.09^\circ\)
The angle of refraction in water is approximately 22.09°.
Example 2: Calculate the critical angle for the interface between glass (refractive index = 1.5) and air (refractive index = 1.0).
Solution: The critical angle (θc) is given by:
\(\displaystyle\sin \theta_c = \frac{n_2}{n_1}\)
Given: n1 = 1.5 (glass); n2 = 1.0 (air)
Substitute the values:
\(\displaystyle\sin \theta_c = \frac{1.0}{1.5} = \frac{2}{3} \approx 0.6667\)
Now find (θc):
\(\displaystyle\theta_c = \sin^{-1}(0.6667) \approx 41.81^\circ\)
The critical angle for the interface between glass and air is approximately 41.81°.
Example 3: A swimming pool appears to be 1.2 meters deep when viewed from directly above. If the refractive index of water is 1.33, calculate the actual depth of the pool.
Solution: The apparent depth (dapparent) is related to the actual depth (dactual) by the refractive index (n):
\(\displaystyle d_{\text{apparent}} = \frac{d_{\text{actual}}}{n}\)
Given: dapparent = 1.2 meters; n = 1.33
Rearrange to find (dactual):
\(\displaystyle d_{\text{actual}} = d_{\text{apparent}} \times n = 1.2 \times 1.33 = 1.596 \text{ meters}\)
The actual depth of the pool is approximately 1.596 meters.
Example 4: A light ray passes through a prism with an apex angle of 60° and a refractive index of 1.5. If the angle of incidence on one face of the prism is 40°, calculate the angle of refraction as the ray exits the prism.
Solution: First, use Snell’s Law to find the angle of refraction at the first face:
\(\displaystyle n_1 \sin \theta_1 = n_2 \sin \theta_2\)
Given: n1 = 1.0 (air); n2 = 1.5 (prism); θ1 = 40∘
Substitute the values:
\(\displaystyle 1.0 \sin 40^\circ = 1.5 \sin \theta_2\)
Since (\(\displaystyle\sin 40^\circ \approx 0.6428\)):
\(\displaystyle 0.6428 = 1.5 \sin \theta_2\)
\(\displaystyle\sin \theta_2 = \frac{0.6428}{1.5} \approx 0.4285\)
Now find (θ2):
\(\displaystyle\theta_2 = \sin^{-1}(0.4285) \approx 25.39^\circ\)
The angle of incidence inside the prism is (θ2). The angle of incidence at the second face of the prism will be (\(\displaystyle 60^\circ – \theta_2\)):
\(\displaystyle 60^\circ – 25.39^\circ = 34.61^\circ\)
Now use Snell’s Law for the second face:
\(\displaystyle n_2 \sin \theta_3 = n_1 \sin \theta_4\)
Given: n2 = 1.5 (prism); n1 = 1.0 (air) ; θ3 = 34.61∘
Substitute the values:
\(\displaystyle 1.5 \sin 34.61^\circ = 1.0 \sin \theta_4\)
Since (\(\displaystyle\sin 34.61^\circ \approx 0.5679\)):
\(\displaystyle 1.5 \times 0.5679 = 1.0 \sin \theta_4\)
\(\displaystyle 0.85185 = \sin \theta_4\)
Now find (θ4):
\(\displaystyle\theta_4 = \sin^{-1}(0.85185) \approx 58.16^\circ\)
The angle of refraction as the ray exits the prism is approximately 58.16°.
Example 5: The speed of light in a vacuum is (3 × 108) m/s. Calculate the speed of light in a medium with a refractive index of 2.4.
Solution: The speed of light in a medium (v) is related to the speed of light in a vacuum (c) by the refractive index (n):
\(\displaystyle v = \frac{c}{n}\)
Given: c = 3 ×108 m/s; n = 2.4
Substitute the values:
\(\displaystyle v = \frac{3 \times 10^8}{2.4} = 1.25 \times 10^8 \text{ m/s}\)
The speed of light in the medium is (1.25 × 108) m/s.
Example 6: A thin lens has radii of curvature (R1 = 20) cm and (R2 = -30) cm. The refractive index of the lens material is 1.6. Calculate the focal length of the lens.
Solution: The lensmaker’s equation for a thin lens is:
\(\displaystyle\frac{1}{f} = (n – 1) \left( \frac{1}{R_1} – \frac{1}{R_2} \right)\)
Given: n = 1.6; R1 = 20 cm; R2 = -30 cm
Substitute the values:
\(\displaystyle\frac{1}{f} = (1.6 – 1) \left( \frac{1}{20} – \frac{1}{-30} \right)\)
\(\displaystyle\frac{1}{f} = 0.6 \left( \frac{1}{20} + \frac{1}{30} \right)\)
Calculate the sum:
\(\displaystyle\frac{1}{20} + \frac{1}{30} = \frac{3}{60} + \frac{2}{60} = \frac{5}{60} = \frac{1}{12}\)
Substitute back into the equation:
\(\displaystyle\frac{1}{f} = 0.6 \times \frac{1}{12} = \frac{0.6}{12} = \frac{1}{20}\)
So:
\(\displaystyle f = 20 \text{ cm}\)
The focal length of the lens is 20 cm.
FAQs
What is refraction of light and why does it occur?
Refraction of light is the bending of light rays as they pass from one medium to another with a different density. It occurs because light travels at different speeds in different media. This change in speed causes the light to change direction at the boundary between the two media.
Can you explain the laws of refraction?
The laws of refraction, also known as Snell’s laws, state two main principles: (1) The incident ray, refracted ray, and the normal to the interface of two media all lie in the same plane. (2) The ratio of the sine of the angle of incidence to the sine of the angle of refraction is constant for a given pair of media, which is known as the refractive index.
What is the refractive index and how does it affect the bending of light?
The refractive index is a measure of how much light slows down in a medium compared to a vacuum. It affects the bending of light; a higher refractive index means light slows down more and bends more sharply. Different materials have different refractive indices, influencing how much light is refracted when entering or exiting the material.
What are the different types of refraction, and how do they occur in nature?
Types of refraction include atmospheric refraction, which causes phenomena like the apparent bending of stars’ light as it passes through the Earth’s atmosphere, and total internal reflection, which occurs when light travels from a medium with a higher refractive index to one with a lower refractive index and is reflected entirely back into the higher-index medium. Another example is refraction at water surfaces, where objects appear bent or displaced.
How does refraction explain the apparent depth of a swimming pool?
Refraction explains the apparent depth of a swimming pool because light rays coming from the bottom of the pool bend as they move from water to air. This bending causes the bottom to appear closer to the surface than it is, making the pool seem shallower than its true depth.
What is the critical angle and how is it related to total internal reflection?
The critical angle is the angle of incidence above which total internal reflection occurs. When light tries to move from a denser medium to a less dense medium, at angles greater than the critical angle, all the light is reflected into the denser medium instead of refracting. This principle is used in optical fibers to transmit light over long distances with minimal loss.
How do lenses utilize the principles of refraction to form images?
Lenses utilize refraction to converge or diverge light rays, forming images. A convex lens converges light rays to a focal point, creating real or virtual images depending on the object’s position relative to the lens. A concave lens diverges light rays, making them appear to come from a focal point behind the lens, always forming virtual, diminished images. These principles are applied in eyeglasses, cameras, microscopes, and other optical instruments to manipulate light and form clear images.
