For centuries, humans marveled at rainbows, their vibrant colors stretching across the sky after a rain shower. But how did these beautiful arcs form? The answer lay hidden in the mysterious behavior of light. In the seventeenth century, the great scientist Isaac Newton took up the challenge of unraveling this enigma.
In 1666, when Newton was just 23 years old, he performed a simple yet profound experiment with light. He used a glass prism to investigate the phenomenon of colors. The common belief was that the spectrum of rainbow colors produced when white light passed through a prism was due to some property of the prism itself. However, Newton discovered something remarkable: the colors were already inherent in the light itself.
Newton’s experiment involved a beam of white light (similar to sunlight) entering a glass prism. As the light passed through, it bent or refracted. The prism separated the white light into its constituent colors: red, orange, yellow, green, blue, indigo, and violet. Each color bent at a different angle, creating the beautiful spectrum we see in rainbows.
Newton’s key insight was that the colors were not alterations of light caused by the prism. Instead, they were original and inherent properties of light itself. To test this idea, Newton used a lens to refocus the many-hued spectrum back into a single, merged beam. Surprisingly, this reconstituted beam appeared white. He then passed this recombined beam through another prism, demonstrating that it could once again be split into a spectrum, just as before.
Newton didn’t immediately share his results. It took him six years to report his findings to the Royal Society in London. His book “Opticks”, published in 1704, documented his experiments and theories about light. In it, he revealed the true nature of colors and the role of prisms. Newton’s work not only explained rainbows but also laid the foundation for our understanding of optics and the behavior of light.
What is Refraction?
Refraction is the bending of light as it passes from one medium to another. When light travels from air (a less dense medium) to glass (a denser medium), it changes direction due to differences in the speed of light in these materials. This bending occurs because light travels at different speeds in different media, following Snell’s Law.
Imagine you’re swimming in a pool, and you look at your legs through the water’s surface. They appear slightly shifted or bent, right? That’s a refraction. When light travels from air (a less dense medium) to glass (a denser medium), it changes direction due to differences in the speed of light in these materials.
Refraction occurs because of the change in speed experienced by a wave when it crosses a boundary between two different materials. For example, when light travels from air into water, its speed decreases. As a result, it bends towards the normal (an imaginary line perpendicular to the surface). Conversely, when light moves from a denser substance (like glass) to a less dense one (like air), it speeds up and bends away from the normal.
Laws of Refraction: Two important laws govern refraction:
– First Law: The incident ray, refracted ray, and the normal (at the point of incidence) all lie in the same plane.
– Second Law (Snell’s Law): The ratio of the sine of the angle of incidence (i) to the sine of the angle of refraction (r) is constant:
\(\displaystyle \frac{\sin i}{\sin r} = \text{constant} \)
Snell’s law helps us calculate how much light bends when it crosses a boundary between two media.
Examples:
- The twinkling of Stars: Ever wondered why stars twinkle? It’s due to atmospheric refraction. Starlight undergoes several refractions while reaching Earth through the gradually changing refractive index of our atmosphere.
- Optical Instruments: Refraction allows us to create optical instruments like magnifying glasses, lenses, and prisms. These tools manipulate light to help us see better or focus images.
What is a Prism?
A prism is a transparent optical element with flat, polished surfaces. Imagine it as a transparent, polished flat object that can bend or refract light. It typically has two triangular bases and three rectangular lateral surfaces. Prisms are made from materials like glass, plastic, or even fluorite. They have two identical ends (like a triangle, square, or rectangle) and flat faces or surfaces. They can disperse white light into its component colors, creating beautiful rainbows.
The most common shape of a prism is the triangular prism, which has a triangular base and two rectangular sides. When light passes through a prism, it gets bent or refracted at each surface due to changes in its speed and direction.
When light travels from one medium to another (like air to glass), its speed changes. This change causes the light to bend as it enters the new medium. The angle at which light hits the surface of the medium and the refractive indices (a fancy term for how much light slows down in different materials) determines how much the light bends. Prisms can split white light into its constituent colors. When a narrow beam of white light enters a prism, it emerges as a beautiful sequence of colors: violet, indigo, blue, green, yellow, orange, and red. This phenomenon is called dispersion.
Each color in white light has a different wavelength. When light passes through a prism, the shorter wavelengths (like violet) bend more, while the longer wavelengths (like red) bend less. The result? A rainbow-like spectrum! The violet light bends the most, and the red light bends the least.
Refraction through a Glass Prism
When a ray of light enters a glass prism, it bends towards the normal (an imaginary line perpendicular to the surface) because glass is denser than air. As the light exits the prism, it bends away from the normal. The emergent ray deviates from the incident ray, forming an angle known as the angle of deviation.
Imagine you have a glass prism—a transparent, three-sided object with two triangular bases and three rectangular lateral surfaces. When a beam of light enters the prism, something magical happens. The light bends or refracts as it moves through the glass. But why does this bending occur?
As the light ray approaches the surface of the prism, it encounters a change in medium. Glass is denser than air, so the light slows down when it enters the prism. According to Snell’s law, light traveling from a rarer medium (like air) to a denser medium (like glass) bends towards the normal (an imaginary line perpendicular to the surface). So, the incident ray bends towards the normal.
Now, the light ray moves through the glass prism. As it reaches the other surface (the base of the prism), it’s time for another change. This time, the light exits the glass and enters the air. The speed of light increases, and it bends away from the normal. The emergent ray takes a different path than the incident ray.
The angle between the incident ray and the emergent ray is crucial. We call it the angle of deviation. When the angle of incidence equals the emergence angle, the deviation angle is minimum. In other words, when the light ray passes symmetrically through the prism, it experiences the least deviation.
When white light (which contains all colors) enters the prism, it splits into its component colors. Each color (like violet, blue, green, etc.) has a different wavelength. Because of this, they bend by varying amounts. Violet light bends the most (shortest wavelength), while red light bends the least (longest wavelength). The result? White light scatters into a beautiful spectrum of colors—just like a rainbow.
Derivation of Refractive Index of a Prism
The refractive index of a prism is a measure of how much light gets bent or refracted as it passes through the prism. It’s defined as the ratio of the speed of light in a vacuum (where light travels at its maximum speed) to the speed of light in the prism. In other words, it tells us how much the prism slows down the light compared to its speed in space.
When light enters a prism, it changes its direction due to differences in the optical density of the prism material (usually glass). The refractive index quantifies this change. If the refractive index is higher, light bends more as it enters the prism.
A higher refractive index means that light slows down more in the prism. This leads to greater bending or refraction. Different materials (like glass, water, or diamond) have distinct refractive indices, affecting how they interact with light.
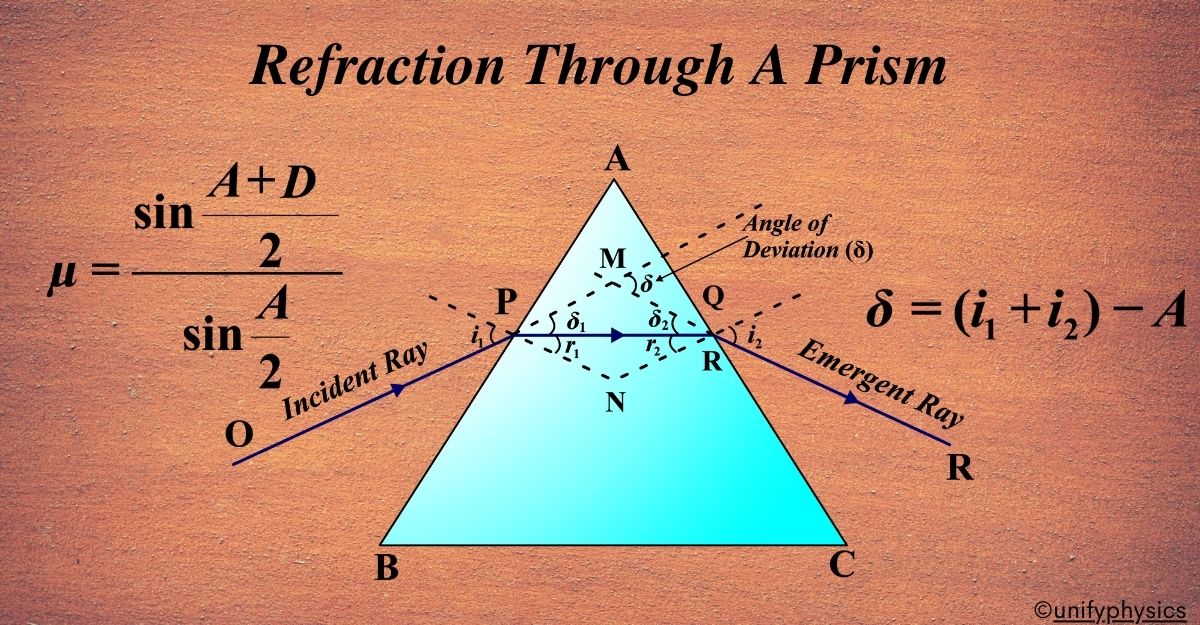
The refractive index of a prism (µ) relates the angle of the prism (A) and the angle of minimum deviation (ẟm):
\(\displaystyle \mu = \frac{\sin A + \delta_m/2}{\sin A/2} \)
We start with Snell’s Law, which states that:
\(\displaystyle\mu = \frac{\sin i}{\sin r}\)
For a prism, the minimum deviation occurs when the light ray travels parallel to the base of the prism, and the angles of refraction are equal. In this condition, the angle of incidence (i1) is equal to the angle of emergence (i2).
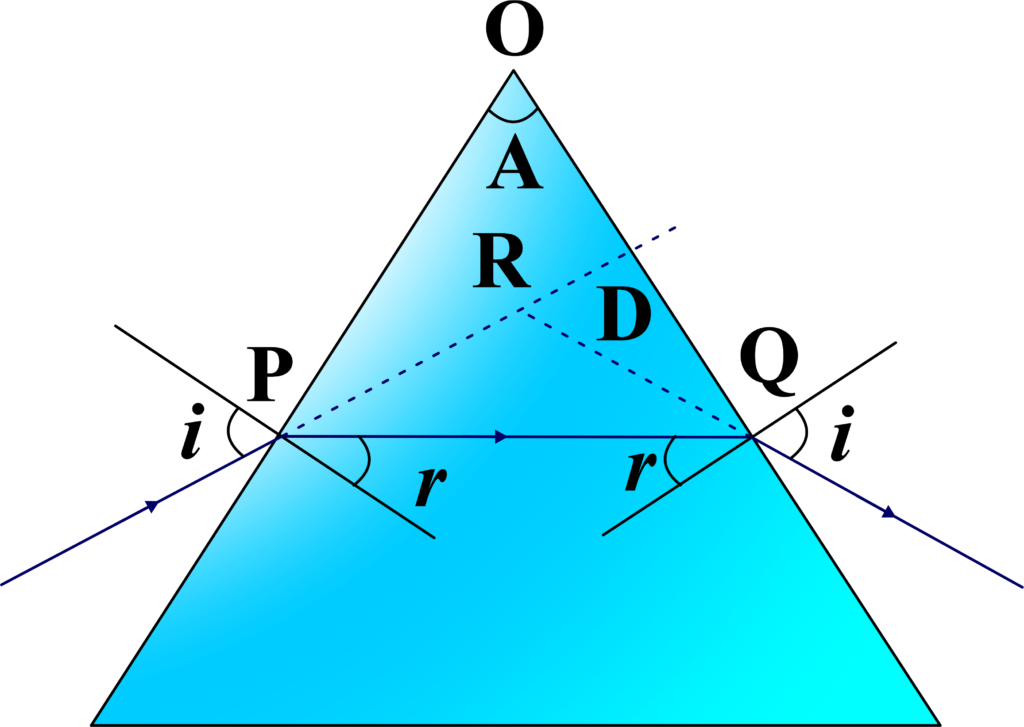
Considering the triangle ( \(\displaystyle\triangle OPQ \)):
\(\displaystyle A + \angle OPQ + \angle OQP = 180^\circ\)
Since the normals at points (P) and (Q) are considered, the angles inside the prism become:
\(\displaystyle \angle OPQ = 90^\circ – r\)
\(\displaystyle\angle OQP = 90^\circ – r\)
Substituting these into the angle sum:
\(\displaystyle A = 180^\circ – (90^\circ – r + 90^\circ – r) = 2r\)
Therefore,
\(\displaystyle r = \frac{A}{2} \quad \text{…(1)}\)
Considering the triangle ( \(\displaystyle\triangle PQR\)): Using the exterior angle theorem, we get:
\(\displaystyle D = \angle RPQ + \angle RQP\)
Since ( \(\displaystyle\angle RPQ = i – r \)) and ( \(\displaystyle\angle RQP = i – r \)), we get:
\(\displaystyle D = (i – r) + (i – r) = 2i – 2r\)
Rearranging this equation, we get:
\(\displaystyle D + 2r = 2i\)
Substituting (\(\displaystyle r = \frac{A}{2} \)) from equation (1), we get:
\(\displaystyle D + A = 2i \quad \text{…(2)}\)
Therefore,
\(\displaystyle i = \frac{A + D}{2} \quad \text{…(3)}\)
Using Snell’s Law at the first surface of the prism:
\(\displaystyle\mu = \frac{\sin i}{\sin r}\)
Substituting the values of (i) and (r) from equations (3) and (1):
\(\displaystyle\mu = \frac{\sin \left(\frac{A + D}{2}\right)}{\sin \left(\frac{A}{2}\right)}\)
The refractive index (µ) of the prism is given by:
\(\displaystyle\begin{equation}\label{eqn:1}\boxed{\boldsymbol{\mu = \frac{\sin \left(\frac{A + D}{2}\right)}{\sin \left(\frac{A}{2}\right)} }} \end{equation}\)
The refractive index of a prism depends on the prism angle (A) and the angle of minimum deviation (D). This derivation provides a clear understanding of how light behaves when passing through a prism and helps determine the refractive properties of the prism material.
Angle of Deviation
The angle of deviation (δ) tells us how much the emergent ray has deviated from the incident ray. When the angle of incidence equals the emergence angle, the deviation angle is minimum.
The angle of deviation is a critical phenomenon related to the behavior of light when it passes through a prism. Imagine you have a glass prism, and you shine a beam of light through it. As the light enters and exits the prism, it changes direction. The angle formed between the initial path the light should have taken and the actual deviated path is called the angle of deviation.
We denote the angle of deviation using the Greek letter δ (pronounced as “delta”). Mathematically, it’s the angle between the direction of the incident ray (the incoming light) and the direction of the emergent ray (the light that exits the prism).
When light enters a prism, it bends due to differences in the refractive index of the prism material (usually glass). The amount of bending depends on the wavelength of the light and the refractive index of the material. Different colors (wavelengths) of light bend by varying amounts, creating the beautiful spectrum we see when white light passes through a prism.
The angle of deviation is least when the light ray travels parallel to the base of the prism. In this condition, the angle of incidence equals the angle of emergence. This minimum deviation angle is crucial for understanding how prisms disperse light into its component colors. The angle of deviation helps us design optical systems, such as spectroscopes and cameras. By controlling the angle of deviation, we can analyze and manipulate light for various applications.
Angle of Deviation Derivation for Thin Prisms
The angle of deviation is the angle formed between the direction of the incident ray (the incoming light) and the direction of the emergent ray (the light that exits the prism). In other words, it’s the difference in angle between the initial path that the beam should have taken and the actual deviated path after passing through a prism.
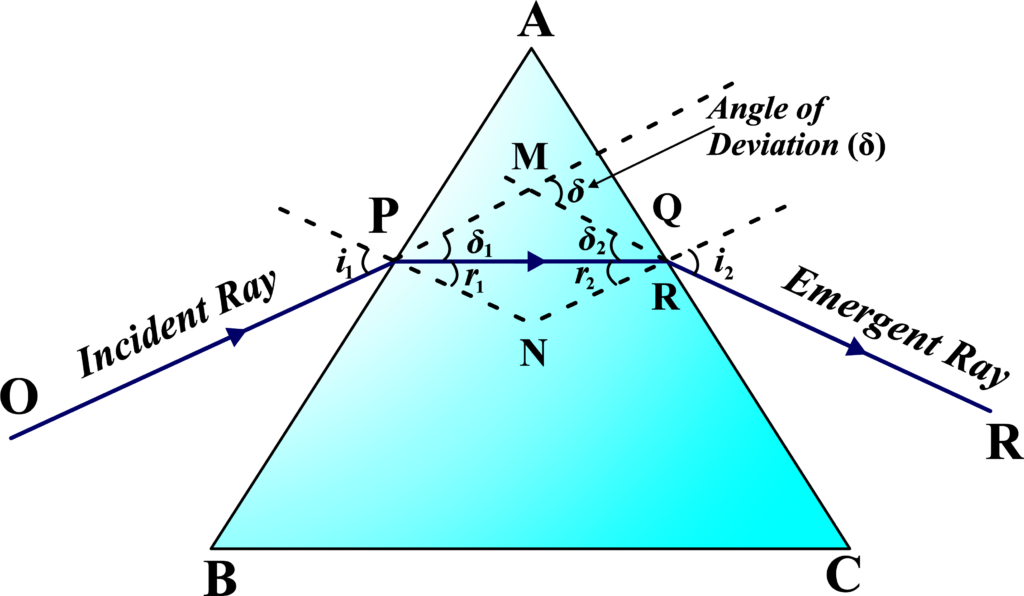
To understand the concept of the angle of deviation in a prism, we will derive its expression step by step, using the given diagram as a reference. The diagram represents a light ray passing through a prism:
- ( \(\displaystyle\angle A\) ) is the prism angle (also called the angle of the prism).
- (i1) and (i2) are the angles of incidence and emergence, respectively.
- (r1) and (r2) are the angles of refraction inside the prism.
- (ẟ) is the total angle of deviation.
In the triangle ( \(\displaystyle \triangle MPQ \)) by the exterior angle theorem, we get:
\(\displaystyle \delta = \delta_1 + \delta_2\)
where (δ1) and (δ2) are the deviations at points ( P ) and ( Q ), respectively.
From the geometry of the prism, we know:
\(\displaystyle\delta_1 = i_1 – r_1\)
\(\displaystyle \delta_2 = i_2 – r_2\)
Therefore, the total deviation (δ) can be written as:
\(\displaystyle \delta = (i_1 – r_1) + (i_2 – r_2)\)
Simplifying, we get:
\(\displaystyle \delta = i_1 + i_2 – (r_1 + r_2)\)
In ( \(\displaystyle \triangle ONP \)), the sum of the angles inside the prism is:
$latex \displaystyle\angle ONP + r_1 + r_2 = 180^\circ
Let ( \(\displaystyle\angle ONP = \theta \)). Thus, the equation becomes:
\(\displaystyle \theta + r_1 + r_2 = 180^\circ\)
In quadrilateral (APNQ), the sum of angles is:
$latex \displaystyle A + 90^\circ + \theta + 90^\circ = 360^\circ
Simplifying this, we get:
\(\displaystyle A + \theta = 180^\circ\)
Therefore,
\(\displaystyle\theta = 180^\circ – A\)
Substituting (θ) back, we have:
\(\displaystyle(180^\circ – A) + r_1 + r_2 = 180^\circ\)
This simplifies to:
\(\displaystyle r_1 + r_2 = A\)
Using ( \(\displaystyle r_1 + r_2 = A\)) in the deviation equation, we get:
\(\displaystyle \delta = i_1 + i_2 – A\)
Therefore, the angle of deviation (δ) for a prism is:
\(\displaystyle \delta = (i_1 + i_2) – A\)
The angle of deviation (δ) in a prism is given by the formula:
\(\displaystyle\begin{equation}\label{eqn:2}\boxed{\boldsymbol{\delta = (i_{1} + i_{2}) – A }} \end{equation}\)
where (i1) is the angle of incidence, (i2) is the angle of emergence, and (A) is the angle of the prism. This formula helps in understanding how the light bends when passing through a prism, and it is crucial for various applications in optics.
Also Read: Refraction At A Spherical Surface
Types of Prism
There are several types of prisms, including:
- Dispersive Prism: Dispersive prisms are used to split white light into its constituent colors. When white light enters a dispersive prism, it bends differently for each color due to varying wavelengths. The violet light bends the most, and the red light bends the least. This phenomenon is called dispersion. The classic triangular prism that creates rainbows when sunlight passes through it.
- Reflective Prism: Reflective prisms are used to reverse, rotate, or deviate light beams. These prisms rely on total internal reflection. They have polished surfaces that reflect light internally. Binoculars, periscopes, and reflecting telescopes use reflective prisms.
- Polarizing Prism: Polarizing prisms split light into components of different polarization. The Nicol prism is a common polarizing prism used in optical devices.
- Beam-Splitting Prism: As the name suggests, these prisms split a single beam of light into two or more beams. Beam splitters are used in various optical instruments, including cameras and laser systems.
- Deflecting Prism: Deflecting prisms change the direction of light by a fixed angle. The wedge prism has a very shallow angle (usually 3 degrees or less) between its input and output surfaces.
Solved Examples
Example 1: A ray of light is incident on a prism with an angle of incidence of 45°. The prism has an apex angle of 30° and a refractive index of 1.5. Calculate the angle of deviation.
Solution: To calculate the angle of deviation, we need to apply Snell’s law at both surfaces of the prism.
Step 1: Calculate the angle of refraction at the first surface. Using Snell’s law at the first surface:
\(\displaystyle n_1 \sin i = n_2 \sin r_1\)
Given: (n1 = 1) (air); ( i = 45°) ; (n2 = 1.5)
\(\displaystyle \sin 45° = 1.5 \sin r_1\)
\(\displaystyle \frac{\sqrt{2}}{2} = 1.5 \sin r_1\)
\(\displaystyle \sin r_1 = \frac{\sqrt{2}}{3}\)
\(\displaystyle r_1 = \arcsin \left( \frac{\sqrt{2}}{3} \right)\)
\(\displaystyle r_1 \approx 28.07°\)
Step 2: Calculate the angle of incidence at the second surface. Using the geometry of the prism:
\(\displaystyle r_1 + r_2 = A\)
Given: ( A = 30° )
\(\displaystyle 28.07° + r_2 = 30°\)
\(\displaystyle r_2 = 30° – 28.07° \approx 1.93°\)
Step 3: Calculate the angle of refraction at the second surface. Using Snell’s law at the second surface:
\(\displaystyle n_2 \sin r_2 = n_1 \sin e\)
\(\displaystyle 1.5 \sin 1.93° = \sin e\)
\(\displaystyle \sin e \approx 1.5 \times 0.0337 \approx 0.05055\)
\(\displaystyle e \approx 2.90°\)
Step 4: Calculate the angle of deviation.
\(\displaystyle \delta = i + e – A\)
\(\displaystyle \delta = 45° + 2.90° – 30°\)
\(\displaystyle \delta = 17.90°\)
The angle of deviation is approximately 17.90°.
Example 2: Derive the formula for the refractive index of a prism given its angle of minimum deviation (\delta_m) and the prism’s apex angle (A).
Solution: At the angle of minimum deviation, the light ray passes symmetrically through the prism. Therefore, the angles of incidence and refraction at both surfaces are equal, denoted as (i) and (r), respectively.
From the geometry of the prism:
\(\displaystyle r_1 = r_2 = r\)
\(\displaystyle r = \frac{A}{2}\)
The angle of deviation at minimum deviation is given by:
\(\displaystyle\delta_m = 2i – A\)
\(\displaystyle i = \frac{\delta_m + A}{2}\)
Using Snell’s law at the first surface:
\(\displaystyle n_1 \sin i = n_2 \sin r\)
Given that (n1 = 1) (air):
\(\displaystyle\sin i = n \sin r\)
\(\displaystyle\sin \left( \frac{\delta_m + A}{2} \right) = n \sin \left( \frac{A}{2} \right)\)
Therefore, the refractive index (n) of the prism is:
\(\displaystyle n = \frac{\sin \left( \frac{\delta_m + A}{2} \right)}{\sin \left( \frac{A}{2} \right)}\)
The refractive index of the prism is
\(\displaystyle n = \frac{\sin \left( \frac{\delta_m + A}{2} \right)}{\sin \left( \frac{A}{2} \right)}\)
Example 3: For a thin prism with a small apex angle (A) and refractive index (n), derive the approximate expression for the angle of deviation (δ).
Solution: For thin prisms, the angles involved are small, and we can use the small-angle approximation:
\(\displaystyle\sin \theta \approx \theta\)) and (\(\displaystyle\tan \theta \approx \theta\)
Using the small-angle approximation:
\(\displaystyle\sin A \approx A\)
From Snell’s law, the angle of deviation (\delta) is given by:
\(\displaystyle\delta = (n – 1)A\)
For thin prisms, the angle of deviation is (\(\displaystyle\delta \approx (n – 1)A\)).
Example 4: A prism with an apex angle of 40° has a minimum deviation angle of 38°. Calculate the refractive index of the prism.
Solution: Given; Apex angle, (A = 40°); Minimum deviation angle, (ẟm = 38°)
Using the formula for the refractive index:
\(\displaystyle n = \frac{\sin \left( \frac{\delta_m + A}{2} \right)}{\sin \left( \frac{A}{2} \right)}\)
\(\displaystyle n = \frac{\sin \left( \frac{38° + 40°}{2} \right)}{\sin \left( \frac{40°}{2} \right)}\)
\(\displaystyle n = \frac{\sin 39°}{\sin 20°}\)
\(\displaystyle n = \frac{0.6293}{0.3420} \approx 1.84\)
The refractive index of the prism is approximately 1.84.
Example 5: A ray of light passes through a prism with an apex angle of 60° and a refractive index of 1.6. If the angle of incidence is 50°, calculate the angle of refraction at the first surface.
Solution: Using Snell’s law at the first surface:
\(\displaystyle n_1 \sin i = n_2 \sin r\)
Given:(n1 = 1 ) (air); ( i = 50° ); ( n2 = 1.6 )
\(\displaystyle\sin 50° = 1.6 \sin r\)
\(\displaystyle 0.7660 = 1.6 \sin r\)
\(\displaystyle\sin r = \frac{0.7660}{1.6} \approx 0.47875\)
\(\displaystyle r = \arcsin(0.47875) \approx 28.6°\)
The angle of refraction at the first surface is approximately 28.6°.
Example 6: Derive the expression for the angle of deviation (ẟ) for an equilateral prism (A = 60°) and refractive index (n) when the ray passes symmetrically.
Solution: For an equilateral prism, the apex angle (A = 60°).
Step 1: Calculate the angle of incidence (i) and angle of refraction (r). In a symmetric passage, the angle of incidence equals the angle of emergence, and both angles of refraction are equal.
From Snell’s law:
\(\displaystyle n = \frac{\sin i}{\sin r}\)
For minimum deviation (ẟm):
\(\displaystyle\delta_m = 2i – A\)
Since the ray passes symmetrically:
\(\displaystyle i = \frac{\delta_m + A}{2}\)
Rewriting the refractive index:
\(\displaystyle n = \frac{\sin \left( \frac{\delta_m + A}{2} \right)}{\sin \left( \frac{A}{2} \right)}\)
The expression for the refractive index (n) is:
\(\displaystyle n = \frac{\sin \left( \frac{\delta_m + 60°}{2} \right)}{\sin 30°}\)
FAQs
What is refraction through a prism and how does it differ from refraction through a plane surface?
Refraction through a prism involves the bending of light as it passes through the angled surfaces of the prism. Unlike a plane surface, a prism has two non-parallel surfaces, causing the light to refract twice—once when it enters the prism and again when it exits. This results in the light emerging at an angle different from its original path, leading to phenomena such as dispersion.
What is the angle of deviation in the context of a prism?
The angle of deviation is the angle between the incident light ray entering the prism and the emergent light ray exiting the prism. It represents the total change in the light ray’s direction due to refraction within the prism. The angle of deviation depends on the prism’s angle, the light’s wavelength, and the refractive index of the prism material.
How does the angle of deviation change with the angle of incidence?
The angle of deviation varies with the angle of incidence. Initially, as the angle of incidence increases, the angle of deviation decreases reaches a minimum value, and then increases again. The minimum deviation occurs at a specific incidence angle where the light passes symmetrically through the prism.
What is the significance of the minimum angle of deviation in a prism?
The minimum angle of deviation is significant because it provides a simple way to calculate the refractive index of the prism material. At this angle, the light path inside the prism is symmetrical, making the derivation of the refractive index straightforward. This concept is used in spectrometry to measure material properties.
How is the refractive index of a prism derived using the angle of minimum deviation?
The refractive index of a prism can be derived by measuring the angle of minimum deviation and knowing the prism’s angle. By applying principles of refraction and using geometric relationships within the prism, the refractive index can be calculated. This derivation involves understanding how light bends at the prism surfaces and the symmetry at minimum deviation.
What is the angle of deviation derivation for thin prisms and how does it differ from that of thick prisms?
The angle of deviation derivation for thin prisms simplifies the analysis by assuming the prism’s angle is small. This approximation allows for straightforward calculations, showing that the deviation angle is directly proportional to the prism’s angle and the refractive index difference. For thick prisms, the calculations are more complex due to larger angles and more pronounced refraction effects.
How does understanding refraction through a prism help in practical applications like spectroscopy?
Understanding refraction through a prism is crucial in spectroscopy, where prisms are used to disperse light into its component colors (spectrum). By analyzing the angles of deviation for different wavelengths, scientists can determine the composition of light sources. This principle is used in various fields, including material analysis, astronomy, and chemical identification.