The concept of resonance comes from the Latin word “resonantia,” which means “echo” or “to resound”. It was first observed in acoustics, particularly in musical instruments. For example, when a string of a guitar is plucked, it vibrates and produces sound. If another string is tuned to the same note, it will start to vibrate too, even without being touched. This is called sympathetic resonance.
Resonance as a scientific concept began to take shape with the study of mechanical systems. Scientists noticed that certain structures would naturally vibrate at specific frequencies. These natural frequencies are what we now call resonant frequencies.
By the end of the 19th century, the idea of resonance expanded beyond acoustics to other areas of physics and engineering. It became a key concept in understanding how systems respond to external forces.
Today, resonance is a fundamental principle across various fields. It’s used to describe phenomena in mechanical, electrical, acoustic, and even molecular systems. Whether it’s a bridge vibrating in the wind or an MRI machine in a hospital, resonance plays a crucial role.
Electrical Resonance
Electrical resonance is like a dance between electricity and components in a circuit. It happens when an AC (alternating current) circuit really likes a particular frequency and decides to ‘dance’ most energetically at that frequency.
When the circuit is powered by AC voltage, the inductor and capacitor exchange energy. If the frequency of the AC matches the natural ‘dance rhythm’ of the circuit, that’s when you hit resonance. At this frequency, the energy moves back and forth between the inductor and capacitor so perfectly that they seem to cancel each other out, and the circuit ‘dances’ with the least resistance.
Think of pushing a child on a swing. If you push at just the right times, the child swings higher with less effort. That’s resonance. In an electrical circuit, if the AC frequency is just right, the current can flow much easier, and the circuit ‘swings’ with the maximum current.
Electrical resonance is super important in real life. It’s used in radios to tune into your favorite station, in wireless charging to transfer energy efficiently, and in many other electronic devices to make sure they work just right.
Electrical resonance is all about matching the frequency of the AC voltage to the natural frequency of the circuit. When they match, the circuit reaches its peak performance, just like a dancer hitting every beat of the song perfectly.
Resonance in a series RLC circuit is a condition that occurs when the frequency of the voltage source causes the inductive reactance XL to equal the capacitive reactance XC At this point, the circuit’s impedance Z is at its minimum value, and it is purely resistive, meaning XL = XC. This makes the total impedance equal to the resistance R of the circuit.
The formula you’ve provided describes the current amplitude im in terms of the maximum voltage vm, resistance R, inductive reactance XL, and capacitive reactance XC:
\(\displaystyle i_m = \frac{v_m}{Z} = \frac{v_m}{\sqrt{R^2 + (X_C – X_L)^2}}\)
At resonance, since XL = XC, the term XC – XL becomes zero, simplifying the equation to:
\(\displaystyle i_m = \frac{v_m}{R}\)
This means that at resonance, the current amplitude is at its maximum because the impedance is at its minimum (just the resistance R. For example,, you can think of it like tuning a radio to a specific station. When the radio is tuned correctly to the station’s frequency, the sound is clear and has the highest volume. Similarly, when the RLC circuit is ‘tuned’ to the resonant frequency, the current is at its maximum.
When the frequency (ω) of the driving voltage in a series RLC circuit is varied, the circuit will exhibit different behaviors depending on how (ω) compares to the circuit’s natural or resonant frequency (ω0).
Imagine you’re playing a video game where you have to match the speed of an on-screen spinner with the speed of your controller’s joystick. If you match the speeds perfectly, you score maximum points. This is similar to what happens in an RLC circuit.
- Below Resonant Frequency (ω < ω0): The circuit behaves more like a capacitor, as the capacitive reactance XC is higher than the inductive reactance XL. The current lags behind the voltage because the circuit stores energy in the electric field of the capacitor.
- Above Resonant Frequency (ω > ω0): The circuit acts more like an inductor, with XL being higher than XC. The current leads the voltage since the circuit stores energy in the magnetic field of the inductor.
- At Resonant Frequency (ω = ω0): The magic happens here! The inductive and capacitive reactances cancel each other out XL = XC, and the circuit behaves as if it’s purely resistive. The impedance is at its lowest, and the current reaches its maximum amplitude. It’s like hitting the jackpot in the game where your spinner and joystick speeds match perfectly.
Also Read: AC Voltage Applied to a Series LCR Circuit
Resonant Frequency
Every circuit has a special frequency where it works best, called the resonant frequency. It’s like a favorite song that a circuit loves to ‘dance’ to. This favorite frequency depends on two things in the circuit: the inductance (L) and the capacitance (C). The formula to find this special frequency is:
\(\displaystyle\omega_0 = \frac{1}{\sqrt{LC}}\)
At this frequency, the circuit lets the electric current flow easily, just like when you push a swing at just the right time to make it go higher. It’s the perfect condition where everything in the circuit works together smoothly.
Now, when we talk about the resonant frequency, we use a special kind of frequency called angular frequency (ω), which is a bit different from the regular frequency (f) we hear about in music or radio. Angular frequency is like measuring how many times the swing goes around in a circle every second.
Because a full circle has 2π radians (a way to measure angles), we use 2π to change the angular frequency into the regular frequency. That’s why the formula for the regular frequency at resonance looks like this:
\(\displaystyle f_0 = \frac{1}{2\pi\sqrt{LC}} \)
This formula uses 2π to make sure we’re talking about how many times the circuit ‘dances’ to its favorite song every second, which we measure in hertz (Hz), instead of how many circles it makes.
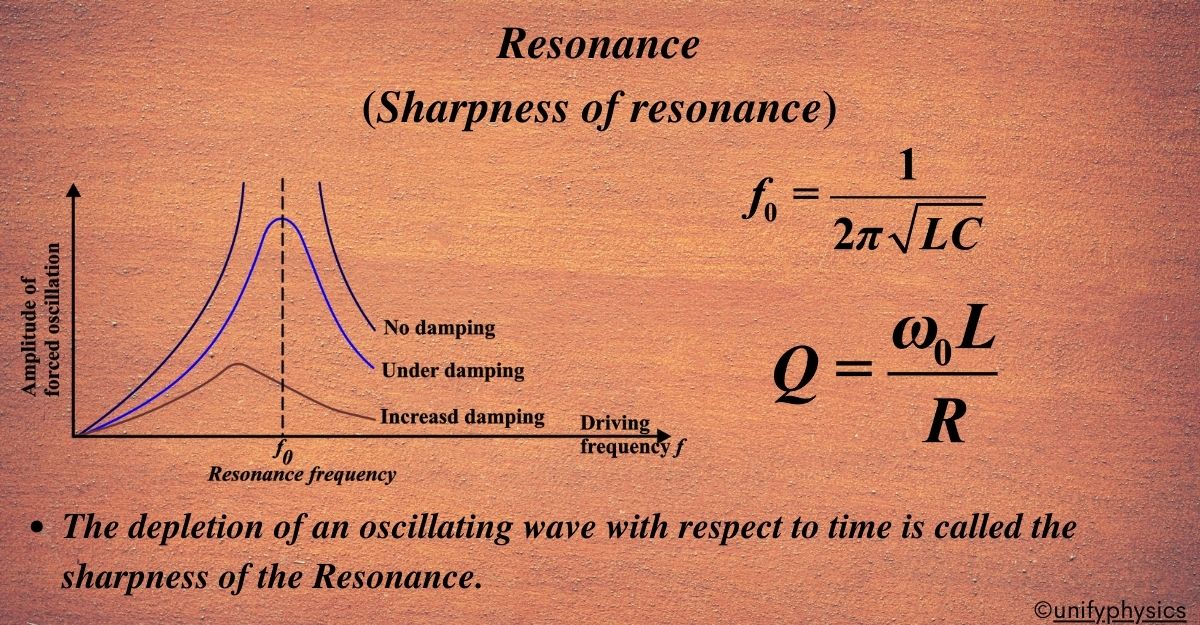
Sharpness of resonance
Sharpness of resonance, often quantified by the Quality Factor (Q), is a measure of how ‘sharp’ or ‘narrow’ the resonance peak is on a graph of amplitude versus frequency. A high Q factor means the system has a sharp resonance, where it strongly prefers its natural frequency and doesn’t respond much to frequencies away from it.
Damping
Now, let’s talk about damping. Damping refers to the loss of energy in an oscillating system due to resistive forces, which could be actual physical resistance or electrical resistance in circuits. Damping reduces the amplitude of the oscillations over time. In an LCR circuit, the resistance component is responsible for damping.
- Increase in Damping: As damping increases, the energy loss per cycle increases, which broadens the resonance curve, making it less sharp. This means the system can resonate over a wider range of frequencies, but with a lower amplitude at the resonant frequency.
- Decrease in Damping: Conversely, if damping decreases, the energy loss per cycle is reduced, leading to a sharper resonance. The system will have a higher amplitude at the resonant frequency and will not resonate as easily at frequencies away from the natural frequency.
- Amplitude and Sharpness of Resonance: When the amplitude of the oscillations increases, it indicates that the system is less damped, and thus, the sharpness of resonance decreases. This is because a higher amplitude suggests that the system is storing more energy and is less selective about the frequency at which it resonates.
For a series LCR circuit or any resonant system, the sharpness of resonance is inversely related to the amplitude and directly related to the damping. A well-damped system has a broader resonance and lower amplitude, while a less damped system has a sharper resonance with a higher amplitude at the resonant frequency. Understanding these relationships is crucial for designing systems that require precise frequency responses, such as radio receivers or musical instruments.
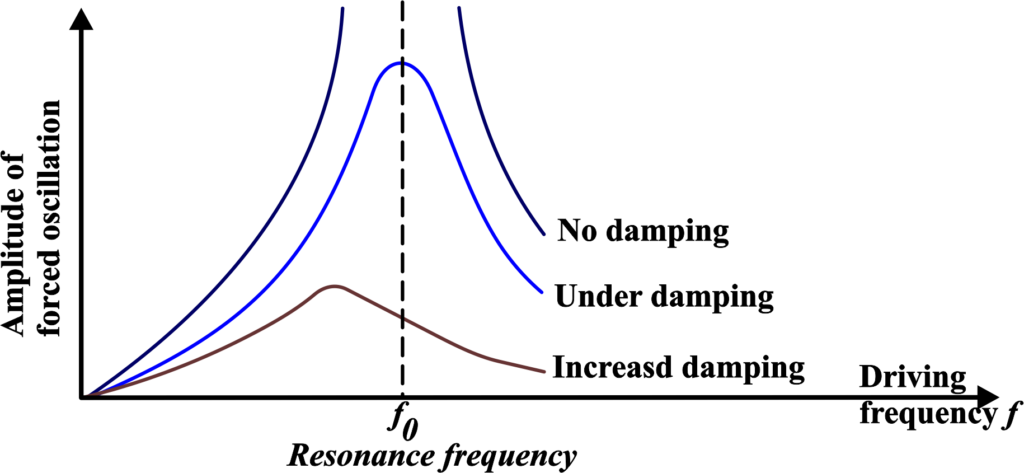
Bandwidth (Δω)
The bandwidth of the circuit is the range of frequencies over which the circuit can effectively resonate. It is defined by the difference between two frequencies, (ω1) and (ω2), at which the current amplitude is \(\displaystyle \frac{1}{\sqrt{2}} \) times the maximum current amplitude. This point is also known as the half-power point because the power at these frequencies is half the power at the resonant frequency.
Quality Factor (Q factor)
The Q factor is a dimensionless parameter that measures the sharpness of resonance. It is defined as the ratio of the resonant frequency (ω0) to the bandwidth (Δω):
\(\displaystyle Q = \frac{\omega_0}{2\Delta\omega}\)
A higher Q factor indicates a sharper resonance, meaning the circuit is more selective and has a narrower bandwidth. Conversely, a lower Q factor means a broader resonance with a wider bandwidth.
Current Amplitude Equation:
The given equation for the amplitude of the current in the series LCR circuit is:
\(\displaystyle i_m = \frac{v_m}{\sqrt{R^2 + (\omega L – \frac{1}{\omega C})^2}}\)
At resonance, we know that the inductive reactance (XL) equals the capacitive reactance (XC), and they cancel each other out. So, the impedance (Z) of the circuit is purely resistive and equals (R). This gives us the maximum current amplitude:
\(\displaystyle i_{m}^{max} = \frac{v_m}{R}\)
Expression for Δω
Now, let’s consider the frequency slightly above resonance, \(\displaystyle(\omega_0 + \Delta\omega)\).
\(\displaystyle i_m = \frac{v_m}{\sqrt{R^2 + \left(\omega_1 L – \frac{1}{\omega_1 C}\right)^2}}\)
The bandwidth (Δω) is defined as the difference between the two frequencies at which the current amplitude falls to \(\displaystyle\frac{1}{\sqrt{2}} \) of its maximum value. This is because the power, which is proportional to the square of the current, is halved at these points. So, we set (im) to \(\displaystyle\frac{1}{\sqrt{2}} i_{m}^{max} \) and solve for Δω:
\(\displaystyle =\frac{{i_{m}^{{\max }}}}{{\sqrt{2}}}=\frac{{{{v}_{m}}}}{{R\sqrt{2}}}\)
\(\displaystyle\sqrt{R^2 + \left(\omega_1 L – \frac{1}{\omega_1 C}\right)^2} = R\sqrt{2}\)
we square both sides, \(\displaystyle R^2 + \left(\omega_1 L – \frac{1}{\omega_1 C}\right)^2 = 2R^2\)
\(\displaystyle\omega_1 L – \frac{1}{\omega_1 C} = R\)
which may be written as,
\(\displaystyle(\omega_0 + \Delta \omega) L – \frac{1}{(\omega_0 + \Delta \omega) C} = R\)
\(\displaystyle\omega_0 L \left(1 + \frac{\Delta \omega}{\omega_0}\right) – \frac{1}{\omega_0 C (\omega_0 + 1 + \frac{\Delta \omega}{\omega_0})} = R\)
When we use the equation \(\displaystyle \omega _{0}^{2}=\frac{1}{{LC}}\) in the second term on the left side, we find…
\(\displaystyle\omega_0 L \left(1 + \frac{\Delta \omega}{\omega_0}\right) – \frac{\omega_0 L}{1 + \frac{\Delta \omega}{\omega_0}} = R\)
We can simplify the expression \(\displaystyle\left(1 + \frac{\Delta \omega}{\omega_0}\right)^{-1} \text{ as } \left(1 – \frac{\Delta \omega}{\omega_0}\right) \text{ since } \frac{\Delta \omega}{\omega_0} \ll 1\) .
\(\displaystyle\omega_0 L \left(1 + \frac{\Delta \omega}{\omega_0}\right) – \omega_0 L \left(1 – \frac{\Delta \omega}{\omega_0}\right) = R\)
\(\displaystyle\omega_0 L \frac{2\Delta \omega}{\omega_0} = R\)
\(\displaystyle\boldsymbol{\Delta \omega = \frac{R}{2L}}\)
The sharpness of resonance is given by,
\(\displaystyle\boldsymbol{ \frac{\omega_0}{2\Delta \omega} = \frac{\omega_0 L}{R}}\)
The quality factor, often denoted as (Q), of a resonant circuit is a measure of the sharpness of its resonance. It is defined as the ratio of the resonant frequency (ω0) to the bandwidth (2Δω). The bandwidth is the difference between the frequencies at which the power across the circuit is half of its maximum value.
The equation you’ve provided seems to be a rearrangement of the quality factor formula. The standard formula for the quality factor in terms of the resonant frequency (ω0), inductance L, and resistance R is:
\(\displaystyle Q = \frac{\omega_0 L}{R} \)
This equation can be derived from the relationship between the resonant frequency, bandwidth, and the quality factor:
\(\displaystyle Q = \frac{\omega_0}{2\Delta \omega} \)
By substituting \(\displaystyle \Delta \omega = \frac{R}{2L}\) into the above equation, we get:
\(\displaystyle Q = \frac{\omega_0}{2\left(\frac{R}{2L}\right)} = \frac{\omega_0 L}{R} \)
\(\displaystyle\boldsymbol{ Q = \frac{\omega_0 L}{R}}\)
So, the quality factor (Q) is directly proportional to the resonant frequency and the inductance, and inversely proportional to the resistance. A higher (Q) indicates a sharper or more selective resonance, meaning the circuit will more effectively filter out frequencies that are not close to the resonant frequency. Conversely, a lower (Q) indicates a broader resonance, where the circuit allows a wider range of frequencies to pass through. This concept is crucial in applications like radio tuners and audio equipment, where selecting specific frequencies without interference from others is essential.
Examples
Example 1: A series LCR circuit has a resistance R = 20Ω, an inductance L = 0.1H, and a capacitance C = 80 μF. Calculate the resonant frequency of the circuit.
Solution: The resonant frequency (f0) of a series LCR circuit is given by the formula:
\(\displaystyle f_0 = \frac{1}{2\pi \sqrt{LC}} \)
Given R = 20Ω, L = 0.1H, and C = 80 μF, we can substitute these values into the formula to find (f0):
\(\displaystyle f_0 = \frac{1}{2\pi \sqrt{(0.1 \, H)(80 \times 10^{-6} \, F)}} \)
\(\displaystyle f_0 = \frac{1}{2\pi \sqrt{0.008}} \)
\(\displaystyle f_0 = \frac{1}{2\pi \times 0.0894}\)
\(\displaystyle f_0 \approx \frac{1}{0.561} \)
\(\displaystyle f_0 \approx 1.78 \, \text{kHz}\)
So, the resonant frequency of the circuit is 1.78 kHz.
Example 2: In a series LCR circuit, the resistance, inductance, and capacitance are R = 100 Ω, L = 0.5 H, and C = 10 μF, respectively. If the quality factor of the circuit is (Q = 10), calculate the sharpness of the resonance.
Solution: The sharpness of resonance (Q) in a series LCR circuit is given by the formula:
\(\displaystyle Q = \frac{1}{R} \sqrt{\frac{L}{C}} \)
Given, R = 100 Ω, L = 0.5 H, and C = 10 μF), we can substitute these values into the formula to find (Q):
\(\displaystyle Q = \frac{1}{100} \sqrt{\frac{0.5}{10 \times 10^{-6}}} \)
\(\displaystyle Q = \frac{1}{100} \sqrt{\frac{0.5}{0.00001}} \)
\(\displaystyle Q = \frac{1}{100} \sqrt{50000} \)
\(\displaystyle Q = \frac{1}{100} \times 223.61 \)
\(\displaystyle Q \approx 2.2361 \)
So, the sharpness of resonance of the circuit is approximately 2.2361.
FAQs
What is resonance in an electrical circuit?
Resonance occurs in an electrical circuit when the reactive components (inductance and capacitance) cancel each other out at a specific frequency, resulting in maximum current flow and minimum impedance.
How does resonance affect an LCR circuit?
In an LCR circuit, resonance occurs when the inductive reactance (XL) equals the capacitive reactance (XC). At resonance, the circuit exhibits maximum current flow, and the impedance is purely resistive.
What is the sharpness of resonance (Q) in an LCR circuit?
The sharpness of resonance (Q) represents the selectivity of an LCR circuit. It is the ratio of resonant frequency (f0) to the bandwidth (∆ω). A higher (Q) value indicates a narrower bandwidth and greater selectivity.
How is the resonant frequency calculated in an LCR circuit?
The resonant frequency (f0) of an LCR circuit is calculated using the formula \(\displaystyle {{f}_{0}}=\frac{1}{{2\sqrt{{LC}}}}\), where (L) is the inductance and (C) is the capacitance.
What factors affect the sharpness of resonance in an LCR circuit?
The sharpness of resonance (Q) in an LCR circuit is affected by the ratio of inductive reactance (XL) to resistance (R). A higher (Q) value is achieved with lower resistance and higher inductance or capacitance. Additionally, losses in the circuit components also affect the sharpness of resonance.