Rutherfords Alpha Scattering Experiment

Before Rutherford’s experiment, the atom was thought to be a ‘plum pudding’—a blob of positive charge with electrons dotted within, like raisins in a pudding. This model was proposed by J.J. Thomson, who had discovered the electron but couldn’t quite figure out how the positive charge was distributed.

Ernest Rutherford, intrigued by the structure of the atom, set out to explore it further. He and his colleagues, Hans Geiger and Ernest Marsden, conducted a series of experiments from 1906 to 1913 at the University of Manchester. The most significant of these took place in 1909.

In this landmark experiment, Rutherford directed alpha particles (helium nuclei) at a thin sheet of gold foil. The prevailing thought was that these particles would pass through with minimal deflection, consistent with the ‘plum pudding’ model.

To the team’s surprise, while most alpha particles passed through, some were deflected at large angles, and a few even bounced back. This was contrary to the expectations set by the Thomson model.

The results led Rutherford to propose a new model: an atom with a central nucleus, containing most of its mass and positive charge, surrounded by space with electrons orbiting this nucleus. This was a radical shift from the ‘plum pudding’ idea.

Rutherford’s experiment fundamentally changed our understanding of the atomic structure. It showed that the atom had a complex structure with a dense nucleus, which later experiments by other scientists would build upon to develop quantum mechanics.

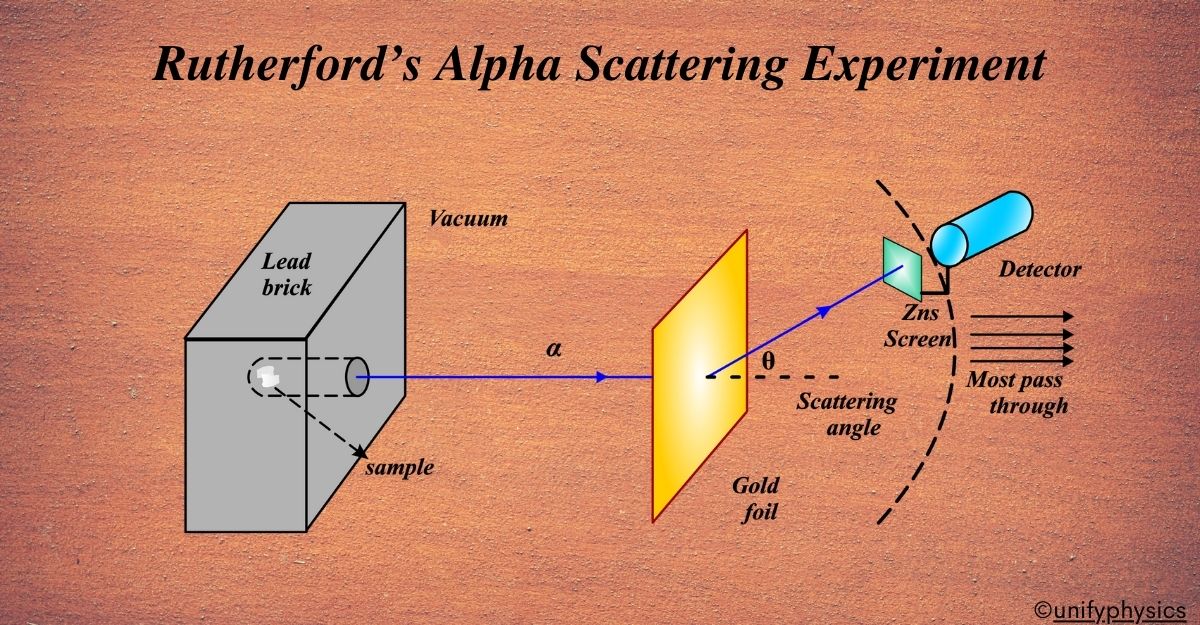
Rutherford’s Alpha Scattering Experiment

In 1911, Ernest Rutherford designed an experiment to test the plum pudding model. He directed a beam of alpha particles (which are helium nuclei) at a thin sheet of gold foil. Rutherford’s experiment led to the idea that an atom resembles a miniature solar system. The nucleus is at the center, like the sun, and the electrons orbit around it, like planets. This was a significant shift from the “plum pudding” model and helped us understand that atoms are mostly empty space with a dense central nucleus.

Alpha particles are essentially helium nuclei, which means they have a positive charge. In the experiment, these particles acted as probes to investigate the internal structure of the atom. Their behavior upon encountering the gold foil provided clues about the atomic structure.

The choice of gold foil was crucial because gold can be hammered into very thin sheets. This allowed the alpha particles to pass through and interact with the atoms measurably. The experiment was groundbreaking because it contradicted the prevailing model of the atom. The surprise came from the fact that some alpha particles were deflected at large angles, indicating a concentrated positive charge at the center of the atom.

This experiment is often considered the birth of nuclear physics. It opened up a whole new field of study, leading to the discovery of protons and neutrons and eventually to the development of quantum mechanics.

Setup And Working of Rutherford’s Alpha Scattering Experiment

Imagine you’re trying to understand what’s inside a mysterious, sealed box. You can’t open it, but you can shake it and listen to the sounds it makes to guess what’s inside. Rutherford’s setup was similar, but instead of shaking a box, he used alpha particles as his ‘sound’.

• Alpha Particle Source: Think of this as a tiny gun that shoots out alpha particles. These particles are like tiny bullets with a positive charge.
• Gold Foil: This is our ‘mysterious box’. It’s incredibly thin, only a few atoms thick. Rutherford chose gold because it can be made into very thin sheets, and it’s also heavy, which means it has lots of protons in its nucleus.
• Detection Screen: This is like our ‘ear’ to ‘listen’ to where the alpha particles end up after hitting the gold foil. It’s coated with a material that glows when an alpha particle hits it.

Working:

At the heart of Rutherford’s experiment was the use of alpha particles. These particles are positively charged and were known to have a relatively large mass, especially compared to electrons. Rutherford utilized these particles as probes to investigate the inner structure of the atom.

The setup of the experiment was ingeniously simple yet effective. Rutherford directed a beam of alpha particles towards a thin sheet of gold foil. Gold was chosen for its ability to be hammered into extremely thin sheets, which was crucial for the experiment. Surrounding the gold foil was a detection screen coated with a material that would produce a flash of light whenever an alpha particle struck it. This allowed Rutherford and his team to observe the behavior of the alpha particles after they encountered the gold atoms.

The working principle of the experiment was based on the expectation that the alpha particles would pass through the gold foil with minimal interaction if the plum pudding model of the atom was correct. This model, proposed by J.J. Thomson, suggested that the atom was a diffuse cloud of positive charge with electrons embedded within it, much like plums in a pudding.

However, Rutherford’s observations challenged this model. He noticed that while many alpha particles did indeed pass through the foil, some were deflected at various angles. This deflection suggested that the alpha particles were encountering something much more substantial than a diffuse cloud of charge.

Rutherford’s interpretation of these results led to the groundbreaking conclusion that the atom must have a dense central core, which he termed the nucleus. This nucleus contained most of the atom’s mass and its positive charge and it was surrounded by empty space through which the electrons moved.

The experiment was a masterclass in scientific inquiry, demonstrating how a well-thought-out experiment could overturn established theories and lead to new scientific understanding. For students learning about Rutherford’s Alpha Scattering Experiment, it’s an excellent example of how empirical evidence can redefine our view of the world at the most fundamental level.

Rutherford’s experiment revealed that the atom is not a uniform blob of positive charge as previously thought, but a complex entity with a dense central nucleus around which electrons orbit.

Observations of Rutherford’s Alpha Scattering Experiment

When Ernest Rutherford set out to explore the structure of the atom, he conducted an experiment that would become a cornerstone of modern physics. The observations from this experiment were both surprising and enlightening, revealing the nature of the atom in a way that had never been understood before.

In Rutherford’s Alpha Scattering Experiment, a beam of alpha particles, which are positively charged and relatively heavy, was directed at a thin sheet of gold foil. The gold foil was chosen because it could be made extremely thin, allowing the alpha particles to pass through and interact with the gold atoms.

The key observations from the experiment were as follows:

• Straight Through Passage: A significant number of alpha particles passed straight through the gold foil without any deflection. This indicated that most of the space within the atom was empty since there was no interaction to alter the particles’ paths.
• Minor Deflections: Some alpha particles were deflected at small angles as they passed through the foil. This suggested that there was something within the atom that could repel the positively charged alpha particles, but it occupied very little space within the atom.
• Rare Large Deflections: A very small fraction of the alpha particles bounced back almost directly toward the source. This was the most surprising observation and implied that a very dense and positively charged center, which would later be known as the nucleus, existed within the atom.

These observations led to the conclusion that the atom is mostly empty space, with a small, dense, positively charged nucleus at its center. The electrons, which were not detected in this experiment, were thought to be orbiting this nucleus, similar to how planets orbit the sun.

Rutherford Atomic Model

The Rutherford Atomic Model was a significant leap forward in our understanding of the atom’s structure. At the center of Rutherford’s model is the nucleus, a tiny but incredibly dense region that contains all of the atom’s positive charge and nearly all of its mass. This nucleus is made up of protons, which carry a positive charge, and later it was discovered, neutrons, which have no charge. The existence of the nucleus was a revolutionary idea at the time because it suggested that instead of being a ‘pudding’ of positive charge, as J.J. Thomson had proposed, the atom had a central core where all the positive charge and mass were concentrated.

Surrounding this tiny nucleus is a vast expanse of empty space. This space is not empty, though; it is where the electrons are found. Electrons are negatively charged particles that are much lighter than the particles in the nucleus. In Rutherford’s model, these electrons orbit the nucleus, much like planets orbit the sun. This comparison to the solar system helped visualize the atom in a way that was easy to understand and marked a significant departure from the plum pudding model.

The electrons orbit at various distances from the nucleus, and these orbits define the size of the atom. Because the electrons are negatively charged and the nucleus is positively charged, there is an electrostatic force of attraction between them. This force keeps the electrons in their orbits and prevents them from spiraling into the nucleus.

Rutherford’s model explained much about the atom’s structure, but it was incomplete. It didn’t explain why the electrons remain in their orbits without losing energy and falling into the nucleus, nor did it account for the specific frequencies of light that atoms emit. The development of quantum mechanics would later answer these questions.

However, the Rutherford Atomic Model was a crucial step in the journey to our current understanding of atomic structure. It shifted the scientific community’s perspective from an atom with no clear structure to one with a defined nucleus and orbiting electrons, setting the stage for future discoveries that would further refine the model.

Scattering of the α-particles

In Rutherford’s Alpha Scattering Experiment, the scattering of alpha particles was a key observation that led to a new understanding of the atomic structure. To explain this to 12th-grade physics students, let’s consider the alpha particles as tiny, positively charged bullets being shot at a target—the gold foil.

When these alpha particles, which are essentially helium nuclei, were fired at the thin gold foil, most of them passed straight through without changing their path. This was expected because if the atom was as Thomson’s model suggested—a ‘plum pudding’ with a spread-out positive charge—the positively charged alpha particles would have little to deflect them.

However, some alpha particles were deflected at small angles, and very few even bounced back the way they came. This was unexpected and could not be explained by the ‘plum pudding’ model. The deflection of the alpha particles indicated that they were coming into contact with something dense and positively charged within the atom.

Rutherford concluded that the atom must have a central core, or nucleus, that contained all of its positive charge and most of its mass. The nucleus was so dense and heavy compared to the alpha particles that it could deflect them, even sending some directly back where they came from. This was like firing a cannonball at a piece of tissue paper and seeing it bounce back—it suggested that there was something much more substantial than the tissue paper in the way.

To understand the scattering of alpha particles and derive the formula for the electrostatic force involved, we’ll need to look at two fundamental principles in physics: Newton’s second law of motion and Coulomb’s law of electrostatic force.

Newton’s Second Law of Motion states that the force acting on an object is equal to the object’s mass multiplied by its acceleration (F = ma). This law will help us understand how the alpha particles’ paths change when they come close to the gold nucleus.

Coulomb’s Law tells us about the force between two charged objects. It says that the force (F) is directly proportional to the product of the charges (q₁ and q₂) and inversely proportional to the square of the distance (r) between them. The law is mathematically expressed as:

\(\displaystyle F = k \frac{q_1 q_2}{r^2} \)

where (k) is Coulomb’s constant, and (q₁) and (q₂) are the charges of the objects.

In the case of Rutherford’s experiment, we’re dealing with alpha particles, which have a charge of (2e) (since they are helium nuclei with two protons), and a gold nucleus with a charge of (Ze) (where (Z ) is the atomic number of gold and (e) is the elementary charge).

Now, let’s derive the formula for the force experienced by an alpha particle as it approaches the gold nucleus. According to Coulomb’s law, the force of repulsion (F) between the alpha particle and the nucleus is given by:

\(\displaystyle F = \frac{1}{4\pi\varepsilon_0} \frac{(2e)(Ze)}{r^2} \)

This is the force that acts on the alpha particles and causes them to scatter when they come close to the nucleus. It’s a central concept in understanding the results of Rutherford’s experiment and the structure of the atom. The scattering of the alpha particles showed that the atom is mostly empty space, with a small, dense, positively charged nucleus at its center.

Alpha-Particle Trajectory

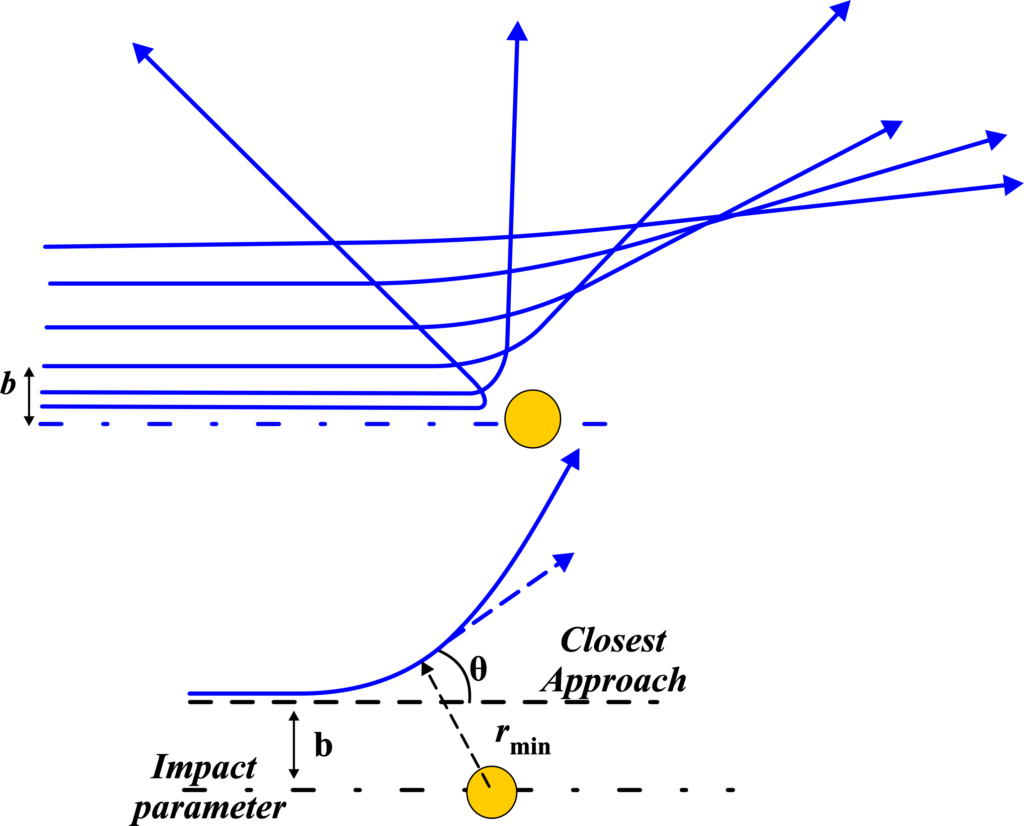
When we talk about the trajectory of alpha particles in Rutherford’s experiment, we’re discussing the paths these particles take as they pass close to or collide with the gold atoms in the foil. Imagine you’re playing a game of marbles where your goal is to roll your marble so that it passes as close as possible to a target marble without hitting it. The path your marble takes is similar to the trajectory of an alpha particle. In Rutherford’s experiment, the alpha particles are like the marbles you roll, and the gold atoms’ nuclei are like the target marbles.

The trajectory of an alpha particle depends on its “impact parameter,” which is a fancy term for how close the particle comes to the nucleus of a gold atom. If an alpha particle has a large impact parameter, meaning it’s initially far away from the nucleus, it will likely pass by without much change in its path. However, if the impact parameter is small, and the alpha particle comes very close to the nucleus, the strong positive charge of the nucleus will repel the positively charged alpha particle, causing it to change direction.

This change in direction can be slight or dramatic, depending on how close the alpha particle gets to the nucleus. If it gets extremely close, the repulsion from the nucleus can even send the alpha particle back in the direction it came from. This is similar to your marble game—if you roll your marble too close to the target, it might hit it and bounce back towards you.

So, the trajectory of each alpha particle in Rutherford’s experiment tells us something about the structure of the atom. The fact that most alpha particles passed straight through the foil with little or no deflection suggested that atoms are mostly empty space. The occasional large deflections indicated the presence of a small, dense, positively charged nucleus at the center of the atom.

How did Rutherford interpret the trajectory of alpha particles?

Ernest Rutherford interpreted the trajectory of alpha particles in his experiment as evidence of the atomic structure that was radically different from the then-accepted “plum pudding” model. He observed that most alpha particles passed straight through the gold foil, which suggested that atoms are mostly empty space. However, the key to his interpretation lay in the small number of alpha particles that were deflected at large angles, and even those that rebounded almost directly backward.

Rutherford reasoned that for an alpha particle to be deflected back the way it came, it must have encountered a center of force within the atom that was both dense and positively charged. He deduced that this center of force was the nucleus of the atom—a tiny, dense region where all the positive charge and most of the mass of the atom were concentrated. The trajectories of the alpha particles that were deflected at large angles indicated that they had passed close to these nuclei and had been repelled by the positive charge.

The alpha particles’ paths were hyperbolic, and Rutherford used this information, along with principles of classical mechanics and electromagnetism, to derive his scattering formula. This formula related the scattering angle of the alpha particles to the impact parameter—the distance of the closest approach to the nucleus. The larger the scattering angle, the closer the alpha particle had come to the nucleus, and the more significant the deflection.

Rutherford’s interpretation of the alpha particle trajectories was a pivotal moment in physics, leading to the planetary model of the atom and laying the groundwork for the development of quantum mechanics. It was a brilliant piece of deductive reasoning that changed our understanding of the fundamental structure of matter.

Electron Orbits In Rutherford’s Nuclear Model

Electrons were thought to orbit the nucleus at a distance, similar to how planets orbit the sun, maintaining a balance between electrostatic attraction and their centrifugal force. Imagine the nucleus of an atom as a large sun in the center of a solar system, and the electrons as planets orbiting around this sun. In Rutherford’s model, the electrons orbit the nucleus in paths called orbits or shells. These orbits are not random; they are well-defined paths that keep the electrons at specific distances from the nucleus.

The nucleus itself is positively charged, made up of protons and neutrons. The electrons, which are negatively charged, are attracted to the nucleus because opposite charges attract each other. This attraction is a bit like gravity keeping the planets in orbit around the sun, but instead of gravity, it’s the electromagnetic force that’s at work here.

Now, you might wonder, if the electrons are attracted to the nucleus, why don’t they just crash into it? Well, this is where things get interesting. The electrons are moving at very high speeds in their orbits, and this movement creates a balance. Just as a satellite in space stays in orbit around the Earth because of its speed, electrons maintain their orbits due to their velocity.

In Rutherford’s model, these orbits are not too close to the nucleus, which means there’s a lot of empty space in an atom. Most of the atom is this empty space. The small fraction of alpha particles that were deflected in Rutherford’s experiment showed that the positive charge is concentrated at the center of the atom, in the nucleus, and the electrons are moving around this nucleus in their orbits.

To derive an expression for electron orbits in Rutherford’s Nuclear Model, we’ll need to consider the forces acting on an electron as it orbits the nucleus. In Rutherford’s model, an electron orbits the nucleus similar to how a planet orbits the sun. The nucleus, packed with protons, is positively charged, while the electron is negatively charged. The electrostatic force between the two is analogous to the gravitational force in planetary motion.

• (m_e) as the mass of the electron,
• (v) as the velocity of the electron in its orbit,
• (r) as the radius of the orbit,
• (Z) as the atomic number (number of protons in the nucleus),
• (e) as the elementary charge (charge of the electron),
• (k) as Coulomb’s constant.

The electrostatic force acting as the centripetal force that keeps the electron in its circular orbit is given by Coulomb’s law:

\(\displaystyle F = \frac{k \cdot Z \cdot e^2}{r^2} \)

This force must equal the centripetal force required to keep the electron in circular motion:

\(\displaystyle F = m_e \cdot \frac{v^2}{r} \)

By setting these two expressions equal to each other, we can find the relationship between the velocity of the electron and the radius of its orbit:

\(\displaystyle m_e \cdot \frac{v^2}{r} = \frac{k \cdot Z \cdot e^2}{r^2} \)

Solving for (v), we get:

\(\displaystyle v = \sqrt{\frac{k \cdot Z \cdot e^2}{m_e \cdot r}} \)

This expression tells us the velocity of an electron in its orbit given the radius (r) and the atomic number (Z). It’s important to note that this is a classical approach and doesn’t take into account the principles of quantum mechanics, which are necessary for a complete description of electron behavior in atoms.

The kinetic energy of an electron in orbit around the nucleus can be expressed as:

\(\displaystyle KE = \frac{1}{2} m_e v^2 \)

(m_e) is the mass of the electron
(v) is the velocity of the electron in its orbit

From our previous discussion, we know that the velocity (v) of the electron is given by:

\(\displaystyle v = \sqrt{\frac{k \cdot Z \cdot e^2}{m_e \cdot r}} \)

Substituting this into the kinetic energy formula, we get:

\(\displaystyle KE = \frac{1}{2} m_e \left( \sqrt{\frac{k \cdot Z \cdot e^2}{m_e \cdot r}} \right)^2 \)

Simplifying, we find:

\(\displaystyle KE = \frac{k \cdot Z \cdot e^2}{2r} \)

The potential energy of an electron due to the electrostatic force between the electron and the nucleus is given by:

\(\displaystyle PE = -\frac{k \cdot Z \cdot e^2}{r} \)

The negative sign indicates that the electrostatic force is attractive.

The total energy is the sum of kinetic and potential energies. However, since the potential energy is negative, it subtracts from the kinetic energy:

\(\displaystyle TE = KE + PE \)
\(\displaystyle TE = \frac{k \cdot Z \cdot e^2}{2r} – \frac{k \cdot Z \cdot e^2}{r} \)
\(\displaystyle TE = -\frac{k \cdot Z \cdot e^2}{2r} \)

The total energy is negative, indicating that the electron is in a bound state with the nucleus. The electron would need to gain this amount of energy (in absolute terms) to escape from the atom, which is also known as the ionization energy.

These derivations are based on classical physics and provide a simplified view of the energies involved in Rutherford’s Nuclear Model. In quantum mechanics, the energy levels are quantized, and the calculations are more complex, taking into account the wave nature of electrons.

Also Read: Electron Emission

Limitations of the Rutherford Atomic Model

The Rutherford Atomic Model was a significant advancement in atomic theory, but it had several limitations that were later addressed by more advanced models.

• Electron Energy Loss: According to classical physics, electrons moving in a circular orbit should continuously emit electromagnetic radiation. This is because any charged particle in acceleration, which includes circular motion, emits radiation. If electrons were losing energy, they would spiral inward and eventually crash into the nucleus, causing the atom to collapse. However, we know that atoms are stable and don’t collapse, so there was a contradiction in Rutherford’s model.
• Undefined Electron Orbits: Rutherford’s model didn’t explain why electrons should move in specific orbits around the nucleus. Without a mechanism to define these orbits, the model couldn’t predict the arrangement of electrons in atoms or the chemical properties of elements.
• Spectral Lines: When elements are heated, they emit light at specific wavelengths, creating a spectrum of lines unique to each element. Rutherford’s model couldn’t explain why atoms only emit light at certain frequencies, known as spectral lines.
• Quantum Effects: The model didn’t account for the wave nature of particles, a key aspect of quantum mechanics. It treated electrons as particles moving in definite paths, which is inconsistent with the principles of quantum physics that were developed later.

While Rutherford’s model introduced the concept of a nuclear atom, it was unable to explain the finer details of atomic structure and behavior. These limitations led to the development of the Bohr model and eventually quantum mechanics, which provided a more complete and accurate description of atoms.

FAQs