Semiconductor

The journey of semiconductors is quite fascinating and pivotal to the technology we use today. It all began in the early 19th century with the first documented observation of a semiconductor effect by Michael Faraday in 1833. He noticed that the resistance of silver sulfide decreased with temperature, which was different from metals.

Fast forward to 1874, when Karl Ferdinand Braun discovered conduction and rectification in metal sulfides, which later played a significant role in the development of radio and radar systems. Around the same time, Arthur Schuster found that copper oxide had rectifying properties, adding another semiconductor to the list.

The real game-changer came in the 20th century with the invention of the transistor in 1947 by William Shockley, John Bardeen, and Walter Brattain. This invention revolutionized electronics and paved the way for the development of integrated circuits and the microelectronics industry.

As the years progressed, so did the complexity and capabilities of semiconductor devices. The introduction of doping, where impurities are added to alter the electrical properties of semiconductors, allowed for a wide range of applications, from simple diodes to complex computer processors.

What Are Semiconductors?

Semiconductors are materials that have a unique place on the electrical conductivity spectrum. They are not as conductive as metals, but they’re not insulators either. Imagine a scale where on one end you have materials like copper and silver which allow electricity to pass through them very easily. On the other end, you have materials like rubber or glass that don’t let electricity flow through them at all. Semiconductors sit in the middle of this scale.

The secret to a semiconductor’s ability lies in its atomic structure. Semiconductors are typically made of silicon, which is an element that has four electrons in its outer shell. In a pure silicon crystal, each silicon atom shares its four electrons with four neighboring silicon atoms, creating a strong bond with no free electrons to conduct electricity. This is why pure silicon at room temperature doesn’t conduct electricity well.

However, the conductivity of semiconductors can be greatly increased by adding certain impurities, a process known as doping. This can provide extra electrons or create ‘holes’ (missing electrons) that act as positive charge carriers. When an electric field is applied, these charge carriers (electrons and holes) move and create an electric current.

The beauty of semiconductors is their versatility. By carefully choosing the type and amount of doping, we can control the electrical properties of a semiconductor. This makes them incredibly useful for creating a wide range of electronic devices, from the simplest diodes to the most complex computer chips.

In essence, semiconductors are the building blocks of modern electronics, enabling the creation of devices that can switch and amplify electrical signals, store information, and much more. Their ability to conduct electricity under certain conditions is what makes our smartphones, computers, and all sorts of gadgets possible.

Holes and Electrons in Semiconductors

In the context of semiconductors, we often talk about two types of charge carriers: electrons and holes. But what exactly are they? Electrons are subatomic particles that carry a negative charge. In conductors, like metals, these electrons are free to move around, which is why metals are good at conducting electricity. However, in semiconductors, the situation is a bit different.

Semiconductors, such as silicon, have their electrons bound tightly to their atoms under normal conditions. These electrons are part of the atomic bonds and don’t contribute to electrical conductivity. But when energy is added to the semiconductor (like heat or light), some electrons gain enough energy to break free from their atomic bonds. Once free, these electrons can move through the material and conduct electricity. These free electrons are what we refer to when we talk about electron charge carriers in semiconductors.

Now, when an electron leaves its place in the atomic structure, it leaves behind a vacancy. This vacancy is called a hole. Even though it’s just an absence of an electron, it behaves as if it were a particle with a positive charge. Why? Because if an adjacent electron fills this hole, the hole appears to move in the opposite direction to the electron that filled it.

Think of it like a game of musical chairs. When the music stops (energy is added), an electron (a player) gets up and moves to a new position (higher energy level), leaving an empty chair (a hole). If another electron fills that empty chair, the hole appears to have moved to the position of the second electron.

In a semiconductor, when an electric field is applied, both free electrons and holes play a role in conducting electricity. Electrons move toward the positive side, while holes move towards the negative side. This movement creates an electric current, which is the flow of charge.

The interaction between electrons and holes is fundamental to how semiconductors work and is the basis for creating various electronic devices. By controlling the number of electrons and holes, we can design semiconductors to perform specific functions, like amplifying signals or switching currents on and off.

Mobility of Electrons and Holes:

Mobility is a measure of how quickly charge carriers (which can be electrons or holes) can move through a semiconductor when an electric field is applied. It’s an important property because it affects how well a semiconductor can conduct electricity and is crucial for the design of electronic devices.

Mobility of Electrons: Electrons are negatively charged particles that are one of the primary charge carriers in semiconductors. The mobility of electrons is typically higher than that of holes because electrons are lighter and can move more easily through the crystal lattice of the semiconductor. This means that when an electric field is applied, electrons can quickly respond and drift toward the positive electrode.

Mobility of Holes: Holes, on the other hand, are the absence of an electron in the atomic lattice and act as positive charge carriers. The mobility of holes is generally lower than that of electrons because a hole’s movement is the result of a neighboring electron filling the vacancy. This process is a bit like a game of tag, where each electron moves to fill the hole left by its neighbor, making the hole appear to move in the opposite direction. Since this involves the shifting of atomic bonds, it’s a slower process compared to the movement of free electrons.

Factors Affecting Mobility:
The mobility of both electrons and holes can be affected by several factors:

• Temperature: As the temperature increases, the atoms in the semiconductor vibrate more. This can scatter the charge carriers and generally reduce mobility.
• Impurities and Doping: The introduction of impurities can provide additional scattering centers for charge carriers, which can reduce their mobility.
• Crystal Quality: Defects in the semiconductor crystal, like dislocations or grain boundaries, can also scatter charge carriers and affect mobility.

Band Theory of Semiconductors

The band theory is a way of representing the energy levels of electrons in a solid. It’s a crucial concept for understanding how semiconductors work at the atomic level.

In isolated atoms, electrons occupy discrete energy levels known as orbitals. When atoms come together to form a solid, these discrete levels blend into bands due to the interaction between atoms. These bands represent ranges of energy that electrons can have within the solid.

In semiconductors, there are two main bands to consider:

• The valence band is the highest range of electron energies where electrons are normally present.
• The conduction band is the range of energies higher than the valence band where electrons can move freely and conduct electricity.

The key to a semiconductor’s behavior lies in the energy gap (or band gap) between these two bands. This gap is what determines whether a material is a conductor, semiconductor, or insulator:

• In conductors, the conduction band and valence band overlap, so electrons can easily move and conduct electricity.
• In semiconductors, there is a small energy gap between the two bands. Electrons can jump from the valence band to the conduction band when they gain enough energy (like from heat or light), allowing them to conduct electricity.
• In insulators, the energy gap is large, so it’s very difficult for electrons to move to the conduction band, which prevents them from conducting electricity.

The band theory helps explain why semiconductors can act like insulators at low temperatures but conduct electricity when they’re heated or exposed to light. It’s also the foundation for understanding how doping changes the electrical properties of semiconductors, which is essential for creating electronic devices like diodes and transistors.

(i) Conduction Band and Valence Band in Semiconductors

The valence band is filled with electrons at an absolute zero temperature. The conduction band is higher in energy and is where electrons can move freely. In the context of semiconductors, the conduction band is a crucial concept. It’s one of the energy bands that electrons can occupy, and understanding it is key to grasping how semiconductors work.

Imagine an electron in a semiconductor as a person sitting in a theater. The theater has two main sections of seats: the lower section (the valence band) and the upper section (the conduction band). The conduction band is like the upper section of seats that are initially empty when the show starts (at absolute zero temperature).

Now, if the person (electron) wants to move around freely and enjoy the show (conduct electricity), they need to be in the upper section where they can move from seat to seat without restriction. The conduction band is similar; it’s the band where electrons have enough energy to break free from their atoms and move freely through the material, allowing them to conduct electricity.

For an electron to get to the conduction band, it needs energy, just like a person needs a ticket to move to the upper section. This energy can come from heat, light, or electrical fields. When an electron gains enough energy, it can jump from the valence band to the conduction band. This process is called excitation.

The conduction band is important because it’s where the action happens in a semiconductor. When electrons are in this band, they can move under the influence of an electric field, and that movement is what we call an electric current. The ability of electrons to move to and within the conduction band is what makes semiconductors so useful in creating electronic devices.

The conduction band in semiconductors is like a special zone where electrons can freely move and participate in conducting electricity. It’s a higher energy state compared to where the electrons usually reside, and it’s essential for the semiconductor’s ability to function in electronic components.

What is the Valence Band?

The valence band is one of the main energy bands in the band theory of solids, particularly semiconductors. To understand the valence band, let’s use an analogy that relates to something familiar: a parking lot. Imagine a parking lot filled with cars. Each parking spot represents an atom in the semiconductor, and each car represents an electron. In this analogy, the valence band is like the ground level of a multi-story parking lot where all the spots are filled with cars. These cars (electrons) are not free to move around because they are parked (bound to atoms). This is the state of the valence band at low temperatures, where electrons are bound within their atoms and cannot conduct electricity.

The valence band plays a crucial role in the electrical properties of semiconductors. It is fully occupied by electrons at absolute zero temperature, meaning all the electrons are in their lowest energy states, bound to the atoms, and there is no room for movement. However, as the temperature increases or energy is provided from an external source (like light), some electrons gain enough energy to leave their parking spots (atoms) and move to a higher energy level, the conduction band. This leaves behind empty spots (holes) in the valence band.

The valence band is significant because it’s the source of the charge carriers that make semiconductor devices work. When electrons leave the valence band, they leave behind holes, which act as positive charge carriers. The movement of these holes, along with the free electrons in the conduction band, is what allows semiconductors to conduct electricity under certain conditions.

The valence band in semiconductors is like the home base for electrons. It’s where they start, and it’s only when they have enough energy to leave this band that they can contribute to electrical conductivity.

(ii) What Is the Fermi Level in Semiconductors?

The Fermi Level is a term used in quantum mechanics and solid-state physics to describe the energy level at which the probability of finding an electron is 50%. It’s a theoretical construct that helps us understand the behavior of electrons in a material.

In semiconductors, the Fermi level plays a crucial role in determining the electrical properties of the material. It’s like the water level in a tank; it tells you how much energy an electron must have to be in the “liquid” state (where it can move freely) as opposed to the “solid” state (where it’s bound to an atom).

In an intrinsic semiconductor (a pure semiconductor without any doping), the Fermi level is exactly in the middle of the energy gap between the conduction band and the valence band. This is because the number of electrons is equal to the number of holes.

However, when a semiconductor is doped with impurities, the position of the Fermi level shifts:

• In an N-type semiconductor (doped with extra electrons), the Fermi level moves closer to the conduction band.
• In a P-type semiconductor (doped with extra holes), the Fermi level moves closer to the valence band.

The position of the Fermi level is important because it affects how easily electrons can be excited to the conduction band to conduct electricity. If the Fermi level is closer to the conduction band, it’s easier for electrons to jump up and become free charge carriers.

The Fermi level is a fundamental concept in semiconductor physics. It’s not a physical place within the material but rather a reference point that helps us predict and understand how electrons will behave in different conditions.

How does doping affect the position of the Fermi level?

Doping a semiconductor significantly affects the position of the Fermi level, which is the energy level at which the probability of finding an electron is 50%. Here’s how it works:

N-Type Doping: When a semiconductor is doped with donor impurities (n-type doping), extra electrons are introduced into the system. These additional electrons increase the electron concentration in the conduction band. As a result, the Fermi level shifts upwards, closer to the conduction band¹². This is because the probability of finding electrons at higher energy levels increases with the addition of donor atoms.

P-Type Doping: Conversely, when a semiconductor is doped with acceptor impurities (p-type doping), holes are created in the valence band. These holes are essentially vacancies where electrons can go, increasing the hole concentration. This causes the Fermi level to shift downwards, closer to the valence band¹². The increased presence of holes means that the energy level where there’s a 50% chance of finding an electron is now lower.

In essence, doping changes the balance of electrons and holes in a semiconductor. For n-type doping, the Fermi level moves up because there are more electrons available at higher energy levels. For p-type doping, the Fermi level moves down because there are more holes available at lower energy levels. The position of the Fermi level after doping is crucial as it determines the electrical properties of the semiconductor and how it will behave in electronic devices.

Properties of Semiconductors

Semiconductors have a set of unique properties that make them essential in the field of electronics and physics. Here are some of the key properties:

Variable Conductivity: Unlike metals, the conductivity of semiconductors can be altered by adding impurities (doping), by changing the temperature, or by exposing them to light. This allows semiconductors to be used in a variety of applications, from simple switches to complex computer processors.

Energy Band Structure: Semiconductors have a valence band filled with electrons and a conduction band where electrons can move freely. The energy gap between these bands determines the semiconductor’s electrical properties.

Response to Temperature: As the temperature increases, the conductivity of semiconductors also increases. This is because heat provides energy for more electrons to jump from the valence band to the conduction band, enhancing conductivity.

Generation and Recombination: In semiconductors, free charge carriers (electrons and holes) can be generated by external energy sources like light (generation). They can also recombine (an electron filling a hole), which is a process that can emit light, making semiconductors useful in optoelectronics.

Effect of Light: When light is absorbed by a semiconductor, it can excite electrons to higher energy levels, creating electron-hole pairs. This property is exploited in devices like photovoltaic cells and photodetectors.

Doping: The process of adding impurities to a semiconductor to change its conductivity is called doping. Doping can create n-type (more electrons) or p-type (more holes) semiconductors, which are fundamental for creating electronic devices like diodes and transistors.

These properties are what make semiconductors so versatile and valuable in modern technology. They allow us to control electrical conductivity in ways that enable the creation of electronic components that are the foundation of all our electronic devices.

Types of Semiconductors

Intrinsic Semiconductors:

An intrinsic semiconductor is the simplest form of a semiconductor, and it’s essentially a pure semiconductor without any significant impurities added to it. The most common intrinsic semiconductor material is silicon.

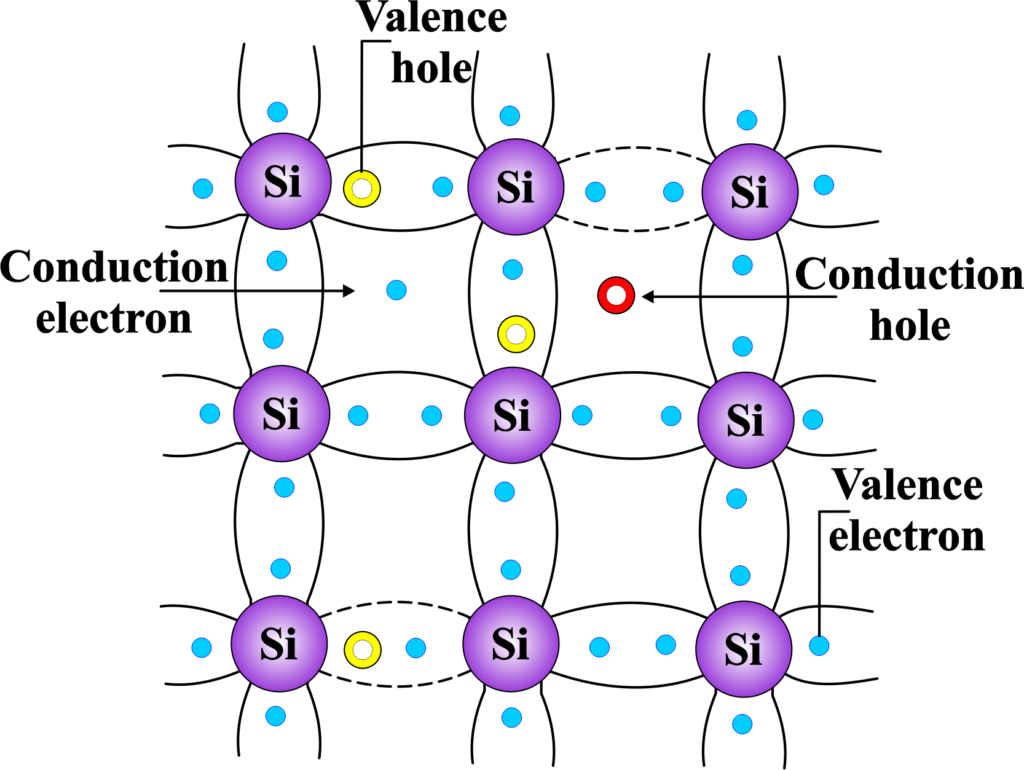
In an intrinsic semiconductor, the number of charge carriers (electrons and holes) is determined solely by the properties of the material itself and not by impurities. At absolute zero temperature, there are no free charge carriers in an intrinsic semiconductor because all the electrons are bound in the valence band. However, as the temperature rises, some electrons gain enough energy to jump across the band gap into the conduction band. When an electron makes this jump, it leaves behind a hole in the valence band.

The beauty of intrinsic semiconductors lies in their simplicity and balance. The number of free electrons is always equal to the number of holes. This means that for every electron that gets excited into the conduction band, there’s a corresponding hole left behind. The electrical conductivity of intrinsic semiconductors is relatively low because there aren’t many charge carriers at room temperature. However, their conductivity increases with temperature, as more electrons are excited to the conduction band.

Intrinsic semiconductors are important because they serve as the base material to which impurities can be added to create extrinsic semiconductors, which have much higher levels of conductivity. They are also used in the fabrication of devices like photodetectors and solar cells, where the purity of the material is crucial for the device’s performance.

Extrinsic Semiconductors:

An extrinsic semiconductor is a semiconductor that has been intentionally “doped” with impurities to change its electrical properties. Unlike intrinsic semiconductors, which are pure and have an equal number of electrons and holes, extrinsic semiconductors have an imbalance in the number of charge carriers due to the addition of these impurities.

The process of doping involves adding a small amount of another element to the semiconductor material. For example, silicon has four electrons in its outer shell. If we dope silicon with phosphorus, which has five outer electrons, we introduce extra free electrons into the material. This makes the silicon an extrinsic semiconductor because its electrical properties have been altered by the doping process.

The reason for doping semiconductors is to enhance their conductivity. By controlling the type and amount of doping, we can create materials that have more free electrons (n-type) or more holes (p-type). This control over the electrical properties is essential for the design and function of electronic devices.

Extrinsic semiconductors are the foundation of modern electronics. They are used to create diodes, transistors, and integrated circuits. These components are the building blocks of all electronic devices, from computers and smartphones to solar panels and LED lights.

N-Type Semiconductor

An N-type semiconductor is created by adding impurities that have more electrons than the semiconductor material, providing extra electrons as charge carriers.

An N-type semiconductor is created when a pure semiconductor, like silicon, is doped with atoms that have more electrons in their outer shell than silicon. Silicon has four electrons in its outer shell, so doping it with an element like phosphorus, which has five outer electrons, introduces extra free electrons into the material.

When phosphorus atoms are added to silicon, four of the phosphorus electrons form covalent bonds with the silicon atoms, just like the silicon atoms do with each other. However, phosphorus has one extra electron that doesn’t have a partner and is free to move around. This extra electron increases the number of charge carriers in the silicon, making it more conductive.

The “N” in N-Type stands for negative because the charge carriers in this type of semiconductor are negatively charged electrons. The more free electrons we have, the more conductive the material becomes, which is why N-type semiconductors are so useful in electronics.

Characteristics of N-Type Semiconductors:

• More Free Electrons: The main characteristic of an N-type semiconductor is that it has more free electrons than holes.
• Doping Element: Elements from group V of the periodic table, like phosphorus, arsenic, or antimony, are typically used for doping to create N-type semiconductors.
• Conductivity: N-type semiconductors have higher electrical conductivity than pure (intrinsic) semiconductors because of the increased number of free electrons.

N-type semiconductors are essential in creating electronic components like diodes and transistors. They are often paired with P-type semiconductors to form p-n junctions, which are the basic building blocks of many electronic devices.

N-type semiconductors are a type of extrinsic semiconductors that have been doped with atoms that contribute additional free electrons, resulting in increased conductivity. They are called N-Type because the majority of charge carriers are negatively charged electrons.

What happens when an N-type semiconductor is exposed to light?

When an N-type semiconductor is exposed to light, several interesting things happen due to the interaction between the light photons and the semiconductor material:

• Photon Absorption: If the energy of the light photons is equal to or greater than the band gap of the semiconductor, the photons can be absorbed by the semiconductor. This energy excites electrons from the valence band to the conduction band.
• Generation of Electron-Hole Pairs: The absorption of photons leads to the generation of additional electron-hole pairs. In an N-type semiconductor, there are already free electrons available due to doping. The incoming light creates more free electrons and corresponding holes.
• Increased Conductivity: The generation of additional charge carriers (electrons and holes) increases the electrical conductivity of the semiconductor. This is because there are more charge carriers available to carry electric current.
• Photocurrent: If there is an external circuit connected to the semiconductor, the movement of these charge carriers can be harnessed as a photocurrent. This is the principle behind devices like photodiodes and solar cells.
• Separation of Charge Carriers: In devices like solar cells, a built-in electric field at the p-n junction can separate the photogenerated electron-hole pairs, preventing them from recombining immediately. This separation contributes to the generation of a voltage across the junction.

The exposure of an N-type semiconductor to light is a fundamental principle behind many optoelectronic devices, where the conversion of light into electrical signals is crucial.

P-Type Semiconductor

A P-type semiconductor is made by doping the material with impurities that have fewer electrons, creating holes as charge carriers. A P-type semiconductor is formed when a pure semiconductor, like silicon, is doped with atoms that have fewer electrons in their outer shell than silicon. Silicon has four electrons in its outer shell, so if we dope it with an element like boron, which has three outer electrons, we introduce ‘holes’ into the material.

When boron atoms are added to silicon, three of the boron electrons form covalent bonds with the silicon atoms. However, since boron has only three electrons to offer, there’s a missing electron, or a ‘hole’, in the bond structure. This hole can move around the lattice as neighboring electrons jump to fill it, effectively creating a positive charge carrier.

The “P” in P-Type stands for positive because the charge carriers in this type of semiconductor are positively charged holes. Even though holes are technically the absence of electrons, they can move through the lattice and carry electric current, much like electrons do in N-type semiconductors.

Characteristics of P-Type Semiconductors:

• More Holes Than Electrons: The main characteristic of a P-type semiconductor is that it has more holes than free electrons.
• Doping Element: Elements from group III of the periodic table, like boron, aluminum, or gallium, are typically used for doping to create P-type semiconductors.
• Conductivity: P-Type semiconductors have higher electrical conductivity than pure (intrinsic) semiconductors because of the increased number of holes, which act as positive charge carriers.

P-type semiconductors are crucial in the electronics industry. They are often used in conjunction with N-type semiconductors to form p-n junctions, which are the fundamental components of many electronic devices, including transistors, diodes, and solar cells.

P-type semiconductors are a type of extrinsic semiconductors that have been doped with atoms that result in an increased number of holes, making them positively charged. They are called P-Type because the majority of charge carriers are positive holes.

Difference between Intrinsic and Extrinsic Semiconductors

Intrinsic semiconductors are undoped, while extrinsic semiconductors are doped with impurities to enhance conductivity.

Aspect	Intrinsic Semiconductor	Extrinsic Semiconductor
Purity	Pure, no intentional doping.	Doped with impurities.
Charge Carriers	Equal number of electrons and holes.	Unequal number of electrons and holes.
Conductivity	Conductivity is significantly affected by temperature.	Higher conductivity due to doping.
Doping	Not doped.	Doped with donor (n-type) or acceptor (p-type) atoms.
Temperature Dependence	Conductivity significantly affected by temperature.	Less sensitive to temperature changes compared to intrinsic.
Material State	Unaltered state of the semiconductor material.	Altered electrical properties due to added impurities.
Use in Devices	Used in pure form for devices like photodetectors.	Used to create p-n junctions in devices like diodes and transistors.

Applications of Semiconductor

Semiconductors are at the heart of modern electronics. Here are some of the key applications:

• Transistors: These are the fundamental building blocks of all modern electronic devices. They act as switches or amplifiers in circuits.
• Diodes: Semiconductors are used to make diodes, which allow current to flow in one direction only. They’re essential in converting AC to DC (rectification).
• Integrated Circuits (ICs): These are complex circuits with millions of transistors, resistors, and other components on a tiny chip. They form the brains of computers and smartphones.
• Solar Cells: Semiconductors are used to convert light energy into electrical energy in solar panels.
• Light Emitting Diodes (LEDs): They are used in a variety of lighting and display applications because they are energy-efficient and have a long life.
• Sensors: Semiconductor-based sensors are used in a wide range of applications, from temperature sensors in electronic devices to motion sensors in security systems.
• Memory Storage: Flash memory devices like SSDs and USB drives use semiconductors to store data.
• Power Devices: Semiconductors are used in power converters and voltage regulators, which are crucial in power supply systems.

These applications show how semiconductors have revolutionized technology, making them an integral part of almost every electronic device we use today.

Disadvantages of Semiconductor

Semiconductors can be sensitive to temperature and radiation, which can affect their performance.

Sensitivity to Temperature: Semiconductors are sensitive to temperature changes. High temperatures can cause an increase in the number of charge carriers, which can lead to overheating and damage.

Material Fragility: Semiconductor materials, like silicon, are more fragile than metals. They can be damaged by impact, stress, or mishandling during the manufacturing process.

Complex Manufacturing: Producing semiconductor devices requires a highly controlled environment, known as a clean room, to avoid impurities that can affect the device’s performance.

Voltage Limitations: Semiconductors have voltage and current limitations. Exceeding these limits can destroy the semiconductor material.

Susceptibility to Radiation: Radiation exposure can create electron-hole pairs in semiconductors, which can disrupt the normal operation of semiconductor devices.

Static Damage: Semiconductors can be damaged by static electricity, which can accumulate and discharge, leading to the breakdown of the semiconductor material.

Also Read: Energy Bands In Solids

Advantages of Semiconductor

They are versatile, can be miniaturized, and have low power consumption, making them ideal for a wide range of applications.

• Miniaturization: Semiconductors can be made very small, allowing for the creation of tiny electronic devices like microprocessors and nanocircuits.
• Energy Efficiency: They require less power to operate compared to traditional conductors, which makes devices more energy-efficient.
• Speed: Semiconductor devices can operate at very high speeds, enabling fast computing and rapid signal processing.
• Cost-Effective: Once the initial manufacturing setup is complete, semiconductor devices can be produced in large quantities at a relatively low cost.
• Reliability: Semiconductor devices are generally reliable and have a long operational life due to the lack of moving parts and resistance to wear and tear.
• Versatility: They can be used to create a wide range of electronic components, from simple diodes to complex integrated circuits.
• Temperature Range: Semiconductors can operate over a wide range of temperatures, making them suitable for various environments.

These advantages make semiconductors indispensable in the field of electronics and technology. They are the reason why we have advanced so much in the development of electronic devices and systems.

Solved Examples

Problem 1: Calculate the intrinsic carrier concentration in silicon at room temperature (300 K). Given that the energy gap (E_g) of silicon is 1.12 eV and the effective density of states in the conduction band ((N_c)) and valence band (N_v) are (\(\displaystyle 2.8 \times 10^{19}) cm(^-3\)) and (\(\displaystyle 1.04 \times 10^{19}) cm(^-3\)) respectively.

Solution: The intrinsic carrier concentration (n_i) in a semiconductor is given by:

\(\displaystyle n_i = \sqrt{N_c N_v} e^{-\frac{E_g}{2kT}} \)

Given: E_g = 1.12 eV)
\(\displaystyle N_c = 2.8 \times 10^{19} \text{ cm}^{-3}\))
\(\displaystyle N_v = 1.04 \times 10^{19} \text{ cm}^{-3}\))
T = 300 K)
\(\displaystyle k = 8.617 \times 10^{-5} \text{ eV/K}\))

First, calculate the exponential term:

\(\displaystyle \frac{E_g}{2kT} = \frac{1.12}{2 \times 8.617 \times 10^{-5} \times 300} = \frac{1.12}{0.051702} \approx 21.66 \)

Now, calculate the intrinsic carrier concentration:

\(\displaystyle n_i = \sqrt{2.8 \times 10^{19} \times 1.04 \times 10^{19}} e^{-21.66} \)

\(\displaystyle n_i = \sqrt{2.912 \times 10^{38}} e^{-21.66} \)
\(\displaystyle n_i = 1.707 \times 10^{19} e^{-21.66} \)

\(\displaystyle e^{-21.66} \approx 3.23 \times 10^{-10} \)

So,

\(\displaystyle n_i \approx 1.707 \times 10^{19} \times 3.23 \times 10^{-10} \)
\(\displaystyle n_i \approx 5.51 \times 10^9 \text{ cm}^{-3} \)

Therefore, the intrinsic carrier concentration in silicon at 300 K is approximately (\(\displaystyle 5.51 \times 10^9 \text{ cm}^{-3}\)).

Problem 2: Given that the electron mobility (µ_n) in a semiconductor is (1500 cm²V·s) and the hole mobility (µ_p) is (450 cm²V·s), calculate the drift velocity of electrons and holes in an electric field of (100 V/cm).

Solution: The drift velocity (v_d) of charge carriers in a semiconductor is given by:

\(\displaystyle v_d = \mu E \)

where (µ) is the mobility and (E) is the electric field.

Given:
\(\displaystyle \mu_n = 1500 \text{ cm}^2/\text{V·s}\))
\(\displaystyle\mu_p = 450 \text{ cm}^2/\text{V·s}\))
E = 100 V/cm)

For electrons:

\(\displaystyle v_{d,n} = \mu_n E = 1500 \times 100 = 150,000 \text{ cm/s} \)

For holes:

\(\displaystyle v_{d,p} = \mu_p E = 450 \times 100 = 45,000 \text{ cm/s} \)

Therefore, the drift velocity of electrons is (150,000 cm/s) and the drift velocity of holes is (45,000 cm/s) in an electric field of (100 V/cm).

Problem 3: Calculate the position of the Fermi level relative to the conduction band edge in intrinsic silicon at 300 K. Given that the effective density of states in the conduction band (N_c) is (\(\displaystyle 2.8 \times 10^{19} \text{ cm}^{-3}\)), in the valence band (N_v) is (\(\displaystyle 1.04 \times 10^{19} \text{ cm}^{-3}\)), and the bandgap (E_g) is 1.12 eV.

Solution: In an intrinsic semiconductor, the Fermi level (E_F) is located at the midpoint between the conduction band edge (E_c) and the valence band edge (E_v) adjusted for the effective density of states:

\(\displaystyle E_F = E_c – \frac{E_g}{2} + \frac{3}{4}kT \ln \left( \frac{N_v}{N_c} \right) \)

Given: E_g = 1.12 eV
\(\displaystyle N_c = 2.8 \times 10^{19} \text{ cm}^{-3}\))
\(\displaystyle N_v = 1.04 \times 10^{19} \text{ cm}^{-3}\))
T = 300 K)
\(\displaystyle k = 8.617 \times 10^{-5} \text{ eV/K}\))

First, calculate the natural logarithm term:

\(\displaystyle \ln \left( \frac{N_v}{N_c} \right) = \ln \left( \frac{1.04 \times 10^{19}}{2.8 \times 10^{19}} \right) = \ln \left( 0.371 \right) \approx -0.991 \)

Now, calculate the position of the Fermi level:

\(\displaystyle E_F = E_c – \frac{1.12}{2} + \frac{3}{4} \times 8.617 \times 10^{-5} \times 300 \times (-0.991) \)

\(\displaystyle E_F = E_c – 0.56 – 0.064 \times (-0.991) \)
\(\displaystyle E_F = E_c – 0.56 + 0.047 \)
\(\displaystyle E_F = E_c – 0.513 \text{ eV} \)

Therefore, the Fermi level is (0.513 eV) below the conduction band edge in intrinsic silicon at 300 K.

Problem 4: A silicon sample is doped with (10¹⁶) phosphorus atoms per cm³. Calculate the electron concentration and the hole concentration in the sample at 300 K. Assume full ionization of dopants and the intrinsic carrier concentration (\(\displaystyle n_i = 1.5 \times 10^{10} \text{ cm}^{-3}\)).

Solution: For an n-type semiconductor, the electron concentration (n) is approximately equal to the donor concentration (N_D), and the hole concentration (p) can be found using the mass action law:

\(\displaystyle n \approx N_D \)
\(\displaystyle np = n_i^2 \)

Given:
\(\displaystyle N_D = 10^{16} \text{ cm}^{-3}\))
\(\displaystyle n_i = 1.5 \times 10^{10} \text{ cm}^{-3}\))

First, calculate the electron concentration:

\(\displaystyle n \approx 10^{16} \text{ cm}^{-3} \)

Next, calculate the hole concentration:

\(\displaystyle p = \frac{n_i^2}{n} = \frac{(1.5 \times 10^{10})^2}{10^{16}} \)
\(\displaystyle p = \frac{2.25 \times 10^{20}}{10^{16}} \)
\(\displaystyle p = 2.25 \times 10^4 \text{ cm}^{-3} \)

Therefore, the electron concentration in the n-type silicon sample is (\(\displaystyle 10^{16} \text{ cm}^{-3}\)) and the hole concentration is (\(\displaystyle 2.25 \times 10^4 \text{ cm}^{-3}\)).

Problem 5: A silicon sample is doped with (\(\displaystyle 5 \times 10^{15}\)) boron atoms per cm³. Calculate the position of the Fermi level relative to the intrinsic Fermi level (E_Fi) at 300 K. Assume full ionization of dopants and the intrinsic carrier concentration (\(\displaystyle n_i = 1.5 \times 10^{10} \text{ cm}^{-3}\)).

Solution: For a p-type semiconductor, the hole concentration (p) is approximately equal to the acceptor concentration (N_A), and the electron concentration (n) can be found using the mass action law:

\(\displaystyle p \approx N_A \)
\(\displaystyle np = n_i^2 \)

Given:
\(\displaystyle N_A = 5 \times 10^{15} \text{ cm}^{-3}\)
\(\displaystyle n_i = 1.5 \times 10^{10} \text{ cm}^{-3}\)

First, calculate the hole concentration:

\(\displaystyle p \approx 5 \times 10^{15} \text{ cm}^{-3} \)

Next, calculate the electron concentration:

\(\displaystyle n = \frac{n_i^2}{p} = \frac{(1.5 \times 10^{10})^2}{5 \times 10^{15}} \)

\(\displaystyle n = \frac{2.25 \times 10^{20}}{5 \times 10^{15}} \)
\(\displaystyle n = 4.5 \times 10^4 \text{ cm}^{-3} \)

The position of the Fermi level relative to the intrinsic Fermi level (E_Fi) can be found using the equation:

\(\displaystyle E_F – E_{Fi} = -kT \ln \left( \frac{N_A}{n_i} \right) \)

Given: \(\displaystyle k = 8.617 \times 10^{-5} \text{ eV/K}\)
T = 300 K

Calculate the natural logarithm term:

\(\displaystyle \ln \left( \frac{N_A}{n_i} \right) = \ln \left( \frac{5 \times 10^{15}}{1.5 \times 10^{10}} \right) = \ln \left( 3.33 \times 10^5 \right) \approx 12.71 \)

Now, calculate the Fermi level position:

\(\displaystyle E_F – E_{Fi} = -8.617 \times 10^{-5} \times 300 \times 12.71 \)
\(\displaystyle E_F – E_{Fi} = -0.328 \text{ eV} \)

Therefore, the Fermi level is (\(\displaystyle 0.328 \text{ eV}\)) below the intrinsic Fermi level in the p-type silicon sample at 300 K.

Problem 6: Calculate the conductivity of intrinsic germanium at room temperature (300 K). Given that the electron mobility (µ_n) is (\(\displaystyle 3900 \text{ cm}^2/\text{V·s}\)), the hole mobility (µ_p) is (\(\displaystyle 1900 \text{ cm}^2/\text{V·s}\)), and the intrinsic carrier concentration (\(\displaystyle n_i = 2.5 \times 10^{13} \text{ cm}^{-3}\)).

Solution: The conductivity (σ) of an intrinsic semiconductor is given by:

\(\displaystyle \sigma = q n_i (\mu_n + \mu_p) \)

where (q) is the charge of an electron (\(\displaystyle 1.6 \times 10^{-19} \text{ C}\)).

Given: \(\displaystyle \mu_n = 3900 \text{ cm}^2/\text{V·s}\)
\(\displaystyle\mu_p = 1900 \text{ cm}^2/\text{V·s}\)
\(\displaystyle n_i = 2.5 \times 10^{13} \text{ cm}^{-3}\)

Calculate the conductivity:

\(\displaystyle \sigma = 1.6 \times 10^{-19} \times 2.5 \times 10^{13} \times (3900 + 1900) \)

\(\displaystyle \sigma = 1.6 \times 10^{-19} \times 2.5 \times 10^{13} \times 5800 \)

\(\displaystyle\sigma = 1.6 \times 2.5 \times 5800 \times 10^{-6} \text{ S/cm} \)

\(\displaystyle \sigma = 23.2 \times 5800 \times 10^{-6} \text{ S/cm} \)

\(\displaystyle \sigma = 134.56 \times 10^{-6} \text{ S/cm} \)

\(\displaystyle\sigma = 1.3456 \times 10^{-4} \text{ S/cm} \)

Therefore, the conductivity of intrinsic germanium at 300 K is approximately (\(\displaystyle 1.35 \times 10^{-4} \text{ S/cm}\)).

FAQs

Q1:

A1:

Q2:

A2:

Q3:

A3:

Q4:

A4:

Q5:

A5:

Q6:

A6:

Q7: