Solenoid

The story of the solenoid begins with the innovative work of André-Marie Ampère, a French physicist whose name is now synonymous with the unit of electric current, the ampere. In the 1820s, Ampère was fascinated by the relationship between electricity and magnetism, which was a hot topic in scientific circles of the time.

Ampère conceived the idea of the solenoid around 1820. He observed that when electric current flows through a wire, it creates a magnetic field around the wire. But he didn’t stop there; he imagined what would happen if the wire was coiled into a helix. Ampère hypothesized that this would amplify the magnetic effect, creating a stronger and more directed magnetic field.

In 1823, Ampère coined the term “solenoid” to describe this device. The word comes from the Greek “σωληνοειδὴς” (sōlēnoeidēs), meaning “pipe-shaped” or “tubular,” reflecting the cylindrical shape of the coil.

The solenoid was more than just a theoretical curiosity; it had practical implications. Ampère’s work laid the groundwork for the development of electromagnets, which are essentially solenoids with an iron core. This invention would go on to revolutionize technology, paving the way for innovations like electric motors and generators.

Ampère’s law, which he discovered in conjunction with his work on solenoids, describes the magnetic field produced by an electric current. This law is a fundamental part of Maxwell’s equations, which are the foundation of classical electromagnetism.

Since Ampère’s time, various types of solenoids have been invented, each with its unique applications and characteristics. The solenoid has become a critical component in many modern devices, from car starters to computer printers.

What Is a Solenoid?

Imagine you have a long piece of wire. Now, coil this wire tightly into a spring-like shape, and you’ve got the basic structure of a solenoid. A solenoid is a special type of electromagnet, which is essentially a magnet powered by electricity.

The solenoid’s design is quite simple: it’s a helical coil of wire, often wrapped around a metallic core, which can be made of materials like iron. This coil has a length that is much greater than its diameter, giving it a cylindrical shape.

A solenoid is a type of electromagnet that consists of a coil of wire wrapped around a metal core. When an electric current flows through the coil, it creates a magnetic field inside and around the coil. But not just any magnetic field—a very controlled and uniform one, especially in the space inside the coil. The magnetic field can be used to move a metal rod or plunger that is attached to the core. This way, a solenoid can convert electrical energy into mechanical energy.

This magnetic field is what gives the solenoid its power. By controlling the electric current, you can control the magnetic field. Increase the current, and the field gets stronger. Reverse the current and the field’s direction changes.

The solenoid’s ability to create a uniform magnetic field in its interior is what sets it apart. This feature is incredibly useful in many applications because it can be used to exert force, move objects, or even generate electrical signals in other devices.

How Does a Solenoid Work?

A solenoid is made up of a coil of wire—think of it like a spring from a pen, but much longer. This coil is often wrapped around a metal core, which is usually made of iron. When we introduce an electric current through the coil, it starts to behave like a magnet. This is because the flow of electricity generates a magnetic field around the wire.

Now, if you’ve ever played with magnets, you know they have a north and south pole. In a solenoid, the coiled wire creates a magnetic field with these poles at each end of the coil. But unlike a regular magnet, the solenoid’s magnetic field can be turned on and off with the electric current.

By coiling the wire, the magnetic field inside the solenoid becomes much stronger and more uniform than it would be around a straight wire. This is where the solenoid gets its power from.

The metal core inside the coil becomes magnetized when the current flows. If the core is free to move, it will slide in or out of the coil, depending on the direction of the current. This movement is the mechanical motion that can do work, like opening a valve or moving a lever.

Right-Hand Thumb Rule: Hold out your right hand with the thumb and fingers extended, making sure they’re all perpendicular to each other. Point your thumb in the direction of the electric current (from positive to negative) in the wire. Curl your fingers. The direction your fingers are curling toward is the direction of the magnetic field lines that wrap around the wire.

If you’re considering negative charges, like electrons, remember that they move opposite to the conventional current direction. So, for negative charges, the magnetic force will be in the opposite direction to what your thumb indicates.

For Solenoids: The Right-Hand Thumb Rule rule helps us to find the direction of the magnetic field and the current in a solenoid.

• If you hold a solenoid in your right hand, such that your thumb points in the direction of the current in the coil, then your fingers will curl in the direction of the magnetic field inside the solenoid.
• If you hold a solenoid in your right hand, such that your fingers curl in the direction of the current in the coil, then your thumb will point in the direction of the north pole of the solenoid.

Role of the Metal Core in a Solenoid:

Enhancing the Magnetic Field: When an electric current passes through the coil of the solenoid, it generates a magnetic field. The presence of a metal core, which is typically made of a ferromagnetic material like iron, amplifies this magnetic field. The metal core does this by concentrating the magnetic lines of flux, which increases the overall magnetic induction of the coil compared to if it just had air inside.

Creating a Stronger Electromagnet: The metal core becomes magnetized when the current flows, turning the solenoid into a strong electromagnet. This is because the ferromagnetic material of the core has a high magnetic permeability, meaning it’s very good at supporting the formation of a magnetic field.

Controlling Movement: In many solenoids, the metal core is movable. When the coil is energized with current, the core moves to increase the magnetic flux linkage by closing the air gap between the core and the coil. This movement can be used to do mechanical work, like opening a valve or pushing a switch.

Improving Performance: The core is often constructed with laminated metal to reduce eddy currents. Eddy currents are loops of electrical current that are induced within the core when it is exposed to a changing magnetic field. By laminating the core, these unwanted currents are minimized, which improves the performance and efficiency of the solenoid.

Other Materials can be used for the Core of a Solenoid:

The core of a solenoid is typically made from materials that have high magnetic permeability, which means they can easily conduct and amplify magnetic fields. Here are some common materials used for solenoid cores:

• Iron: This is the most commonly used material due to its excellent magnetic properties and cost-effectiveness.
• Steel: A variant of iron, steel is also frequently used, especially when additional strength is needed⁵.
• Ferrite: A ceramic-like material that is non-conductive and has good magnetic permeability. It’s useful in high-frequency applications.
• Soft Magnetic Composites (SMCs): These are used in high-current DC solenoids and can handle high current densities without saturating.

In addition to these, solenoid valves may use other materials for their housing, such as:

• Nylon (Polyamide – PA)
• PVC (PolyVinylChloride)
• Brass
• Nickel-plated brass
• Stainless Steel (304 and 316)

The choice of material strongly depends on the chemical properties and the temperature of the medium the solenoid will be exposed to. For example, stainless steel might be chosen for its corrosion resistance, while nylon or PVC might be selected for its insulating properties.

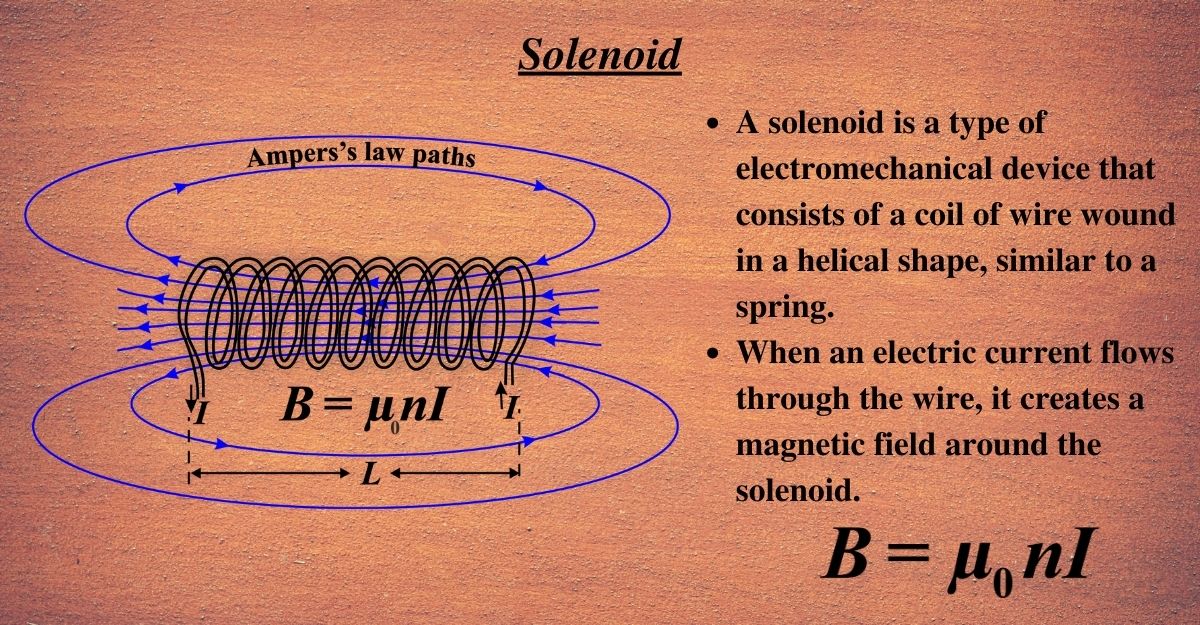
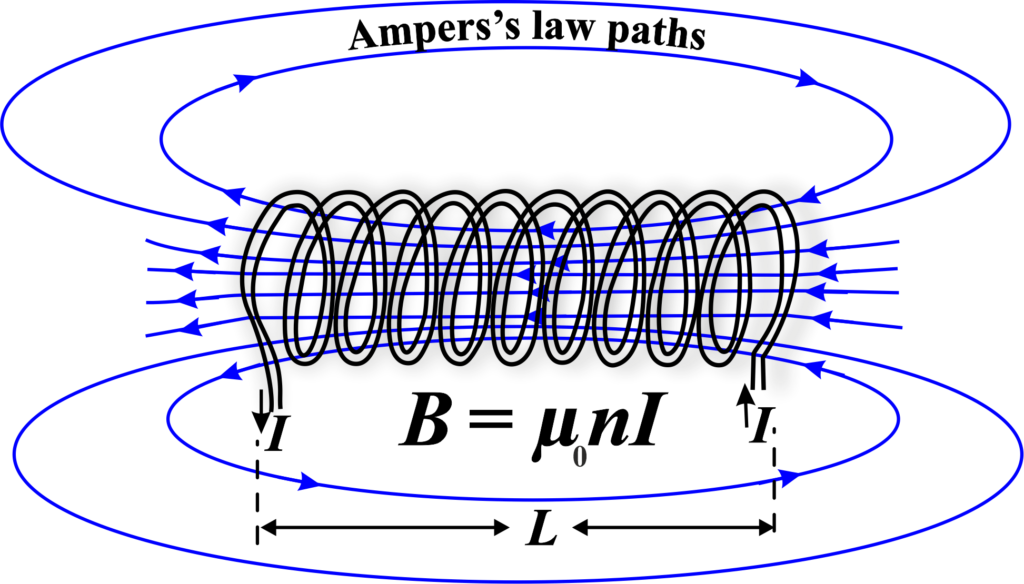
Magnetic Field in a Current-Carrying Solenoid

A solenoid is a coil of wire that produces a magnetic field when an electric current flows through it. The magnetic field inside the solenoid is uniform and parallel to the axis of the coil. The expression for the magnetic field inside the solenoid can be derived using Ampere’s law, which relates the magnetic field around a closed loop to the electric current passing through the loop. Here is a simplified derivation of the expression for the magnetic field inside the solenoid for you:

Suppose we have a solenoid of length L and radius R, with N turns of wire carrying a current I. The number of turns per unit length is n = N / L.

We draw a rectangular loop around the solenoid, as shown in the figure below. The loop has sides a and b, where a is parallel to the axis of the solenoid and b is perpendicular to it.

We apply Ampere’s law to this loop, which states that the line integral of the magnetic field along the loop is equal to the product of the permeability of free space and the net current enclosed by the loop. Mathematically, this can be written as:

\(\displaystyle \oint \vec{B} \cdot d\vec{l} = \mu_0 I_{enc}\)

• \(\displaystyle\vec{B}\) is the magnetic field vector,
• \(\displaystyle d\vec{l}\) is an infinitesimal element of the loop,
• \(\displaystyle\mu_0\) is the permeability of free space,
• \(\displaystyle I_{enc}\) is the net current enclosed by the loop.

The magnetic field is uniform and parallel to the axis of the solenoid inside the solenoid, and negligible outside the solenoid. Therefore, the line integral can be simplified as:

\(\displaystyle\oint \vec{B} \cdot d\vec{l} = B \oint dl = B (2a)\)

where B is the magnitude of the magnetic field and $dl$ is the length of the loop element. The integral is only non-zero for the sides of the loop that are parallel to the axis of the solenoid, which have a length of each.

The net current enclosed by the loop is the sum of the currents in the turns of the solenoid that lie inside the loop. Since the loop has a width of b and the solenoid has a radius of R, the number of turns inside the loop is proportional to the ratio of the areas of the loop and the solenoid cross-section. Therefore, the number of turns inside the loop is:

\(\displaystyle N_{enc} = \frac{b}{R} N\)

The current in each turn is I, so the net current enclosed by the loop is:

\(\displaystyle I_{enc} = N_{enc} I = \frac{b}{R} N I\)

Equating the left-hand side and the right-hand side of the equation, we get:

\(\displaystyle B (2a) = \mu_0 \frac{b}{R} N I\)

Solving for B, we get:

\(\displaystyle B = \frac{\mu_0}{2a} \frac{b}{R} N I\)

If we want to find the magnetic field at the center of the solenoid, we can simply set a = L/2 and b = R in the above expression. This gives us:

\(\displaystyle B = \frac{\mu_0}{L} N I\)

Since n = N / L, we can write this as:

\(\displaystyle\begin{equation}\label{eqn:1}\boxed{\boldsymbol{ B = \mu_0 n I}} \end{equation}\)

This equation tells us that the magnetic field inside a solenoid depends directly on the number of turns per unit length and the current. The more turns or the higher the current, the stronger the magnetic field.

Types of Solenoid

A solenoid is a device that converts electrical energy into mechanical energy by creating a magnetic field inside a coil of wire. There are different types of solenoids based on their design, function, and power source. Here are some common types of solenoids and their features:

AC-Laminated Solenoid: An AC-laminated solenoid is a type of electromagnet that’s designed to work with alternating current (AC). At the heart of an AC-laminated solenoid is a metal core. This core is made up of many thin layers, or laminations, of metal. These layers are insulated from each other, which is important for the solenoid’s function.

Wrapped around this laminated core is a coil of wire. When AC is passed through this coil, it generates a magnetic field just like any other solenoid. The reason for using laminated metal is to reduce what’s called “eddy currents”. These are swirling currents that can occur in the core when it’s exposed to a changing magnetic field, like the one produced by AC. Eddy currents can cause energy loss and unwanted heating. The laminations cut down on these currents, making the solenoid more efficient.

AC-laminated solenoids are known for making a distinctive buzzing sound when they operate. This is because the AC current is constantly changing direction, which causes the core to vibrate slightly.

This type of solenoid can use more strokes than its DC counterpart. A stroke is the distance the solenoid’s plunger moves when activated. More strokes mean the solenoid can be used in applications where a longer movement is needed.

DC C-Frame Solenoid: The “C” in its name comes from the shape of the metal frame that forms part of the solenoid. Imagine a horseshoe or a ‘C’ shaped metal piece that partially surrounds the coil of wire.

When direct current (DC) flows through the coil, the C-frame focuses the magnetic field, which then pulls a movable metal rod, known as the plunger, into the coil. The C-frame design allows for a highly controllable stroke, which is the distance the plunger moves when activated. This makes it ideal for applications that require precise movements.

Because of its design, the DC C-Frame solenoid can be used in a variety of applications, from simple locking mechanisms to more complex machinery used in gaming machines. Although it’s designed for DC, the C-Frame solenoid can also be adapted for use with alternating current (AC) systems, making it a flexible choice for different electrical setups.

DC D-Frame Solenoid: This solenoid gets its name from the shape of its frame. Imagine two ‘D’ shaped metal pieces that form a frame around the coil. This design is sturdy and provides a strong structure for the coil.

When direct current (DC) is passed through the coil, the D-Frame structure helps to focus the magnetic field, which in turn pulls a movable rod, known as the plunger, into the coil. This action is precise and can be repeated many times with consistent results.

Although it’s a DC solenoid, the D-Frame design is also suitable for alternating current (AC) applications. This versatility means it can be used in various settings without needing significant modifications¹.

The D-Frame solenoid can be designed to have a controlled pulse function, which means it can create a magnetic field that turns on and off in a controlled manner. This is particularly useful in applications where timing and precision are crucial.

Linear Solenoid: At its core, a linear solenoid consists of a coil of wire wound around a cylindrical tube. This tube is usually made of a ferromagnetic material like iron. Inside this coil, there’s a movable component called the plunger. It’s also made of a ferromagnetic material and can slide in and out of the coil’s body.

When you pass an electric current through the coil, it becomes an electromagnet. The plunger, which is inside the coil, is attracted toward the center of the coil by the magnetic field created. The movement of the plunger can either push or pull things, depending on how the solenoid is set up. This is the mechanical force that comes from the electrical signal.

The strength and speed of the plunger’s movement are determined by the magnetic field’s strength, which you can control by changing the current’s strength or the number of turns in the coil. When the current is turned off, the magnetic field collapses, and a spring attached to the plunger pushes it back to its original position.

Rotary Solenoid: At its core, a rotary solenoid is designed to convert electrical energy into rotational motion. This means when you power it up, it doesn’t push or pull—it turns. Inside a rotary solenoid, you’ll find a coil of wire and a specially shaped-armature or plunger. This plunger is hinged at a point, and when the coil is energized, the plunger rotates around this hinge point.

When electricity flows through the coil, it creates a magnetic field that causes the armature to rotate. The armature is connected to a shaft, which then turns whatever is attached to it. There’s usually a spring or some other mechanism that returns the armature to its starting position when the power is turned off. This means the solenoid can quickly flip back and forth between positions.

Rotary solenoids are super useful in situations where you need to turn something on and off or back and forth quickly. They’re used in things like vending machines, slot machines, and even some types of cameras.

Energy Stored In a Solenoid

A solenoid doesn’t just create a magnetic field; it also stores energy in that field when an electric current flows through it. First, remember that when current flows through the solenoid, it creates a magnetic field. This field is strongest inside the coil of the solenoid.

The energy is stored in the magnetic field created by the solenoid. It’s like winding up a spring—the more you wind it (or the more current you pass through the solenoid), the more energy it stores.

The amount of energy (E) stored in the magnetic field of a solenoid can be calculated using the formula:

\(\displaystyle E = \frac{1}{2} L I^2 \)

where (E) is the energy in joules, (L) is the inductance of the solenoid in henrys, and (I) is the current in amperes.

The inductance of a solenoid depends on factors like the number of turns in the coil and the material of the core. It’s a measure of how good the solenoid is at storing energy. The current is what you control. More current means more energy stored, but also more heat generated, so there’s a balance to be struck.

Derivation of Energy Stored in a Solenoid: To derive the energy stored in a solenoid, we’ll start with the concept of work done to establish the current in the solenoid’s coil.

When a battery is connected to a solenoid, it works against the opposing induced electromotive force (emf) to establish the current. This work is stored as magnetic energy in the solenoid. The power supplied by the battery can be expressed as (P =Ei ), where (E) is the emf of the battery and (i) is the current.

Since (\(\displaystyle E = iR + L \frac{di}{dt} \))

where (R) is the resistance and (L) is the inductance, the power becomes

\(\displaystyle P = i^2R + Li \frac{di}{dt}\)

The first term (i²R ) represents the power dissipated as heat, and the second term (\(\displaystyle Li \frac{di}{dt}\) ) represents the rate at which energy is being stored in the solenoid. The total energy stored, (U), when the current rises from 0 to (I), is found by integrating the power over time:

\(\displaystyle U = \int_0^I Li \, di \)

\(\displaystyle\begin{equation}\label{eqn:2}\boxed{\boldsymbol{ U = \frac{1}{2} L I^2}} \end{equation}\)

This is the equation for energy stored in the solenoid. The self-inductance (L) of a solenoid is given by

\(\displaystyle L = \mu_0 n^2 A l \)

where (µ₀) is the permeability of free space, (n) is the number of turns per unit length, (A) is the cross-sectional area, and (l) is the length of the solenoid.

Substituting the expression for (L) into the energy equation, we get:

\(\displaystyle U = \frac{1}{2} \mu_0 n^2 A l I^2 \)

If we want to find the energy per unit volume, known as energy density (u), we divide the total energy (U) by the volume (Al) of the solenoid:

\(\displaystyle u = \frac{U}{Al} \)

\(\displaystyle\begin{equation}\label{eqn:3}\boxed{\boldsymbol{u = \frac{1}{2} \mu_0 n^2 I^2 }} \end{equation}\)

This derivation shows that the energy stored in a solenoid is directly proportional to the square of the current and the number of turns per unit length.

Difference between Solenoid and Bar Magnet

A solenoid and a bar magnet are both devices that produce magnetic fields, but they have some differences in their properties and applications. Here is a table that summarizes the main differences between a solenoid and a bar magnet:

Solenoid	Bar magnet
A coil of wire that creates a magnetic field when an electric current flows through it	A piece of metal that has a permanent magnetic field due to the alignment of its atoms
Can create a strong magnetic force that can be controlled by the current	Has a fixed and weak magnetic force that cannot be easily changed
Can be easily demagnetized by turning off the current	Cannot be easily demagnetized unless heated or hammered
Can change the polarity by reversing the direction of the current	Has a fixed polarity that cannot be reversed
Has a uniform magnetic field inside the coil and a negligible magnetic field outside the coil	Has a non-uniform magnetic field that decreases with distance from the poles

Applications of a Solenoid

Solenoids are incredibly versatile and are used in many devices and systems around us. Here are some common applications:

• Electronic Door Locks: Solenoids can act as actuators in electronic locking mechanisms, controlling the lock with the push or pull of the plunger.
• Automotive: In cars, solenoids are used in starter motors to help ignite the engine and in fuel injectors for precise fuel delivery.
• Medical Devices: They are crucial in medical equipment like ventilators and MRI machines, where they help in moving parts with precision and control.
• Industrial Machines: Solenoids are used in various industrial applications, such as controlling valves or as part of the automation process.
• Consumer Electronics: In everyday gadgets like printers and cameras, solenoids are used to control mechanical movements like paper feeding or shutter release.
• Speakers and Microphones: The principle of solenoids is used in speakers and microphones to convert electrical signals into sound and vice versa.
• Water Sprinklers: In irrigation systems, solenoids control the flow of water through valves, allowing for automated watering schedules.

Also Read: Ampère’s Law

Solved Examples

Problem 1: A solenoid has 1000 turns per meter and carries a current of (I = 2 A). Calculate the magnetic field inside the solenoid.

Solution: The magnetic field inside a solenoid is given by:

\(\displaystyle B = \mu_0 n I \)

Given: (\(\displaystyle n = 1000 \, \text{turns/m} \)), (I= 2 A)

\(\displaystyle B = 4\pi \times 10^{-7} \times 1000 \times 2 \)
\(\displaystyle B = 8\pi \times 10^{-4} \, \text{T} \)
\(\displaystyle B \approx 2.51 \times 10^{-3} \, \text{T} \)

The magnetic field inside the solenoid is (\(\displaystyle 2.51 \times 10^{-3} \, \text{T} \)).

Problem 2: A solenoid with 1500 turns per meter carries a current of (3A). Calculate the magnetic field near the end of the solenoid.

Solution: The magnetic field near the end of a solenoid is approximately half the field inside the solenoid:

\(\displaystyle B_{\text{end}} = \frac{1}{2} \mu_0 n I \)

Given: (\(\displaystyle n = 1500 \, \text{turns/m} \)), (I = 3 A)

\(\displaystyle B_{\text{end}} = \frac{1}{2} \times 4\pi \times 10^{-7} \times 1500 \times 3 \)
\(\displaystyle B_{\text{end}} = 2\pi \times 10^{-7} \times 4500 \)
\(\displaystyle B_{\text{end}} = 9\pi \times 10^{-4} \, \text{T} \)
\(\displaystyle B_{\text{end}} \approx 2.83 \times 10^{-3} \, \text{T} \)

The magnetic field near the end of the solenoid is (\(\displaystyle 2.83 \times 10^{-3} \, \text{T} \)).

Problem 3: A solenoid of length (0.5 m) and 2000 turns carries a current of (5 A). Calculate the magnetic field at a point outside the solenoid.

Solution: The magnetic field outside an ideal solenoid is approximately zero due to the cancellation of fields from adjacent turns. However, near the ends, a small field may be present, but it is typically negligible.

The magnetic field outside the solenoid is approximately zero.

Problem 4: A solenoid of length (1m), radius (2 cm), and 1500 turns carry a current of (4 A). Calculate the magnetic flux through the solenoid.

Solution: Magnetic flux (Φ) is given by:

\(\displaystyle \Phi = B \cdot A \)

Given: (\(\displaystyle n = \frac{1500}{1} \, \text{turns/m} \)), (I = 4A), (r = 0.02 m)

\(\displaystyle B = 4\pi \times 10^{-7} \times 1500 \times 4 \)
\(\displaystyle B = 24\pi \times 10^{-4} \, \text{T} \)
\(\displaystyle A = \pi \times (0.02)^2 \)
\(\displaystyle A = \pi \times 4 \times 10^{-4} \, \text{m}^2 \)
\(\displaystyle\Phi = 24\pi \times 10^{-4} \times \pi \times 4 \times 10^{-4} \)
\(\displaystyle \Phi = 96\pi^2 \times 10^{-8} \, \text{Wb} \)
\(\displaystyle \Phi \approx 9.47 \times 10^{-7} \, \text{Wb} \)

The magnetic flux through the solenoid is (\(\displaystyle 9.47 \times 10^{-7} \, \text{Wb}\) ).

Problem 5: A solenoid of length (0.8 m) and 1200 turns carries a current of (6 A). Calculate the energy stored in the magnetic field of the solenoid.

Solution: The energy stored in the magnetic field of a solenoid is given by:

\(\displaystyle U = \frac{1}{2} L I^2 \)

Where:\(\displaystyle L = \mu_0 \frac{N^2 A}{l} \)

Given: (N = 1200), (I = 6 A), (l = 0.8 m), (r = 0.02 m); \(\displaystyle A = \pi r^2 \)

\(\displaystyle L = 4\pi \times 10^{-7} \times \frac{1200^2 \times \pi \times (0.02)^2}{0.8} \)
\(\displaystyle L = 4\pi \times 10^{-7} \times \frac{1440000 \times \pi \times 4 \times 10^{-4}}{0.8} \)
\(\displaystyle L = 4\pi \times 10^{-7} \times \frac{5760\pi \times 10^{-4}}{0.8} \)
\(\displaystyle L = 4\pi \times 10^{-7} \times 7200\pi \times 10^{-4} \)
\(\displaystyle L = 28800\pi^2 \times 10^{-11} \)
\(\displaystyle L \approx 2.84 \times 10^{-5} \, \text{H} \)

\(\displaystyle U = \frac{1}{2} \times 2.84 \times 10^{-5} \times 6^2 \)
\(\displaystyle U = \frac{1}{2} \times 2.84 \times 10^{-5} \times 36 \)
\(\displaystyle U = 1.02 \times 10^{-3} \, \text{J} \)

The energy stored in the magnetic field of the solenoid is (\(\displaystyle 1.02 \times 10^{-3} \, \text{J}\) ).

Problem 6: A solenoid with 1000 turns and length (0.5 m) has a current that changes from (3 A) to (0 A) in (0.02 s). Calculate the induced EMF in the solenoid.

Solution: The induced EMF (\(\displaystyle\mathcal{E}\)) is given by:

\(\displaystyle \mathcal{E} = -L \frac{dI}{dt} \)

Where:\(\displaystyle L = \mu_0 \frac{N^2 A}{l} \)

Given: (N = 1000), (\(\displaystyle\frac{dI}{dt} = \frac{0 – 3}{0.02} = -150 \, \text{A/s}\) ), (l = 0.5 m), (r = 0.01 m); \(\displaystyle A = \pi r^2 \)

\(\displaystyle L = 4\pi \times 10^{-7} \times \frac{1000^2 \times \pi \times (0.01)^2}{0.5} \)
\(\displaystyle L = 4\pi \times 10^{-7} \times \frac{1000000 \times \pi \times 10^{-4}}{0.5} \)
\(\displaystyle L = 4\pi \times 10^{-7} \times 2000\pi \times 10^{-4} \)
\(\displaystyle L = 8000\pi^2 \times 10^{-11} \)
\(\displaystyle L \approx 7.90 \times 10^{-6} \, \text{H} \)

\(\displaystyle \mathcal{E} = -7.90 \times 10^{-6} \times -150 \)
\(\displaystyle \mathcal{E} = 1.185 \times 10^{-3} \, \text{V} \)

The induced EMF in the solenoid is (\(\displaystyle 1.185 \times 10^{-3} \, \text{V}\)).

FAQs