Specific Heat Capacity

In the 18th century, the study of heat and temperature was a hot topic among scientists. One of the key figures in this field was Joseph Black, a Scottish scientist who made groundbreaking observations. He noticed that different substances required varying amounts of heat to achieve the same increase in temperature. This led him to propose the idea of heat capacity, which laid the foundation for the concept of specific heat capacity.

Joseph Black was not just any scientist; he was a curious and meticulous experimenter. He conducted detailed experiments to measure the heat capacities of various substances, using a method known as the ‘method of mixtures’. His work was so influential that it advanced our understanding of heat more than any other philosopher of his time.

Interestingly, the climate played a role in these discoveries. Both Black and his contemporary, Wilcke, who hailed from the colder regions of Scotland and Sweden, respectively, were inspired by their observations of snow and ice. Their chilly environments provided the perfect natural laboratory for studying heat phenomena.

The work of Joseph Black and others set the stage for future scientists to explore the mysteries of heat and temperature. Their early investigations paved the way for the development of the specific heat capacity concept, which is now a fundamental part of thermodynamics.

What is Heat Capacity?

“Heat capacity is the amount of heat energy required to raise the temperature of an object by a certain temperature interval.”

Imagine you’re at the beach on a sunny day. You have two objects with you: a giant iron anchor and a small plastic bucket. If you leave both in the sun, you’ll notice that the bucket heats up quickly, while the anchor takes a lot longer to get warm. This difference is due to their heat capacities.

Heat Capacity is like a measure of how ‘thirsty’ an object is for heat. It tells us how much heat energy (in joules) we need to give to an object to raise its temperature by one degree (either Celsius or Kelvin, as the size of the degree is the same for both scales)¹.

It’s an extensive property, which means it depends on the amount of material. So, the more material you have, the higher the heat capacity. That’s why our giant anchor has a higher heat capacity than the small bucket¹.

In physics, we use the symbol (C) to represent heat capacity. If you want to increase the temperature of an object by a certain amount, you need to supply it with a certain amount of heat energy. The formula looks like this:

\(\displaystyle C = \frac{Q}{\Delta T} \)

Here, (C) is the heat capacity, (Q) is the heat energy supplied, and (∆T) is the temperature change.

Knowing the heat capacity of a material helps us understand how it will behave in different environments. For example, materials with high heat capacities are great for cooking pots because they can absorb a lot of heat without getting too hot too quickly.

Think of the ocean. It has a massive heat capacity, which means it can absorb a lot of heat without a significant temperature change. This property of the ocean helps regulate the Earth’s climate by absorbing heat in the summer and releasing it in the winter.

So, heat capacity is a fundamental concept that helps us predict how different materials will react to heat, which is crucial in many areas of science and engineering. It’s like knowing how much water you can pour into different-sized buckets without them overflowing.

What is Specific Heat Capacity?

” Specific heat capacity is the amount of heat energy required to raise the temperature of 1 kilogram of a substance by 1 degree Celsius (or 1 Kelvin).”

Imagine you’re trying to warm up different types of food in a microwave. Each food item heats up at a different rate, right? Some get hot very quickly, while others take longer. This difference in heating rate is due to a property called specific heat capacity.

Specific Heat Capacity is like the ‘heat personality’ of a substance. It tells us how much heat energy (in joules) is needed to raise the temperature of just 1 kilogram of the substance by 1 degree Celsius (or 1 Kelvin since the size of the degree is the same for both scales).

It’s an intensive property, which means it doesn’t depend on the amount of material. Whether you have a small piece or a large block, the specific heat capacity remains the same.

The formula for specific heat capacity is quite simple:

\(\displaystyle c = \frac{Q}{m\Delta T} \)

Here, (c) is the specific heat capacity, (Q) is the heat energy supplied, (m) is the mass of the substance, and (∆T) is the temperature change.

Specific heat capacity is crucial because it helps us understand how different materials respond to heat. For instance, water has a high specific heat capacity, which means it takes a lot of heat to make it warmer. This is why water is used in car radiators and as a coolant in various industries.

Think about a hot summer day. The land heats up and cools down quickly, but the sea doesn’t. That’s because water has a higher specific heat capacity than soil or sand. This property of water plays a vital role in controlling the climate of coastal areas.

Unit of Specific Heat Capacity: The SI unit is joules per kilogram per degree Celsius (J/kg°C) or joules per kilogram per Kelvin (J/kgK).

Property	Symbol	Unit	Description
Specific Heat Capacity	(c)	J/kg·K or J/kg·°C	The amount of heat required to raise the temperature of 1 kg of a substance by 1 degree.
Molar Specific Heat (at constant pressure)	(Cp)	J/mol·K	The heat capacity of 1 mole of a substance at constant pressure.
Molar Specific Heat (at constant volume)	(Cv)	J/mol·K	The heat capacity of 1 mole of a substance at constant volume.

The specific heat capacity can also be expressed in other units like calories per gram per degree Celsius (cal/g·°C), but the SI unit (J/kg·K) is the standard.

Molar Specific Heat

Molar Specific Heat is the amount of heat energy required to raise the temperature of one mole of a substance by one degree Celsius (or one Kelvin). It’s a measure of how a substance’s temperature changes when it absorbs or loses heat, on a per-mole basis.

Think of molar-specific heat as the ‘heat appetite’ of a mole of a substance. The word ‘molar’ refers to a mole, which is a unit in chemistry that represents a specific number of particles (6.022 x 10²³ particles, to be exact). By talking about molar-specific heat, we’re focusing on the heat capacity of a mole of a substance, rather than a certain mass of it.

The formula for molar specific heat at constant pressure (C_p) is:

\(\displaystyle C_p = \frac{Q}{n\Delta T} \)

where (Q) is the heat added, (n) is the number of moles, and (∆T ) is the temperature change.

Under constant pressure conditions, the pressure of the gas does not change during the process. This is similar to heating a gas in a container with a movable piston. The piston can move up and down to adjust the volume so that the pressure inside remains the same. In terms of energy, at constant pressure, the heat added to the system is equal to the change in enthalpy (which is a measure of the total heat content of a system).

Similarly, molar molar-specific heat at constant volume (C_v), the formula is:

\(\displaystyle C_v = \frac{Q}{n\Delta T} \)

In contrast, constant volume conditions mean that the volume of the gas remains fixed. Imagine heating a gas in a rigid, sealed container. Since the container cannot expand, the volume of the gas cannot change, no matter how much it heats. When it comes to energy, at constant volume, the heat added is equal to the change in the internal energy of the system.

The difference between constant pressure and constant volume is important because it affects how the gas exchanges heat and works on its surroundings. For example, at constant pressure, a gas can do work by expanding against the pressure. But at constant volume, no work is done because the volume doesn’t change. These conditions are also reflected in the specific heat capacities of gases, where (C_p) (specific heat at constant pressure) is typically greater than (C_v) (specific heat at constant volume) because work is done at constant pressure.

Molar specific heat tells us how different substances heat up. It’s like knowing how much a food item will ‘fill up’ the ‘temperature appetite’ of a mole of a substance. This concept is super important in chemistry and physics because it helps us predict how substances will behave when we heat them or cool them down.

In real life, knowing the molar-specific heat of a substance can help us in processes like cooking or industrial heating. For example, metals with low molar specific heat up quickly and are used in things like toasters.

Specific Heat Capacity of Gases

For gases, specific heat capacity can be measured at constant volume (C_v) or constant pressure (C_p).

The first law of thermodynamics is a foundational concept that helps explain the thermal behavior of gases, including their specific heat capacities. The first law of thermodynamics is used to explain the specific heat capacity of gases because it relates the heat added to a gas to the change in its internal energy and the work done by the gas.

The first law tells us that the energy in the universe is constant. In a closed system, the change in internal energy (∆U) is equal to the heat added to the system (Q) minus the work done by the system (W). In equation form, it’s written as:

\(\displaystyle \Delta U = Q – W \)

When we talk about gases, the specific heat capacity can be measured under two different conditions: constant volume (C_v) and constant pressure (C_p). Here’s how the first law helps us understand these concepts:

Constant Volume (C_v): If the volume doesn’t change, the gas doesn’t do any work (since work is a force applied over a distance, and here, there’s no distance moved). All the heat energy (Q) goes into changing the internal energy (∆U), which means raising the temperature of the gas. The specific heat capacity at constant volume tells us how much heat is needed to raise the temperature of a certain amount of gas without allowing it to expand.

Constant Pressure (C_p): At constant pressure, the gas can expand. When it does, it does work on its surroundings. Some of the heat energy (Q) added goes into doing this work (W), and the rest goes into raising the temperature (∆U). The specific heat capacity at constant pressure is higher than at constant volume because some energy is ‘used up’ in doing work.

The specific heat capacity of a gas tells us how much heat is required to raise the temperature of a unit mass of the gas by one degree Celsius (or one Kelvin). For gases, this capacity is influenced by whether the heat is added at constant volume or constant pressure, as explained by the first law of thermodynamics.

Monatomic Gases

Monatomic gases are the simplest type of gases, consisting of single atoms, like helium or neon have specific heat capacities that depend only on their translational motion since they have no rotational or vibrational modes. When we talk about their specific heat capacity, we’re looking at how much heat is needed to raise the temperature of these simple gases.

This law tells us that the energy change in a system is equal to the heat added to it minus the work done by the system. In formula terms:

\(\displaystyle \Delta U = Q – W \)

When we heat a monatomic gas at constant volume, no work is done (since (W = P∆V), and (∆V = 0) at constant volume). So, all the heat (Q) goes into increasing the internal energy (∆ U), which raises the temperature.

Specific Heat at Constant Volume (C_v): For monatomic gases, (C_v) is the amount of heat required to raise the temperature of 1 mole of the gas by 1°C at constant volume. It’s given by the value (\(\displaystyle \frac{3}{2}R \)), where ( R ) is the gas constant.

Monatomic gases have no rotational or vibrational energy levels. They only have translational kinetic energy. So, when you heat them, all the energy goes into increasing this translational motion, which directly translates to a temperature increase.

Monatomic Gases and Degrees of Freedom: Monatomic gases, like helium or neon, are composed of single atoms. These atoms can move in three dimensions: up/down, left/right, and forward/backward. These are called translational degrees of freedom.

At a given temperature (T), the average energy associated with each degree of freedom is (\(\displaystyle \frac{1}{2}k_BT\) ), where ( k_B ) is Boltzmann’s constant.

Internal Energy (U): For one mole of a monatomic gas, we consider all three degrees of freedom. So, the total average energy is (3/2)k_BT) per molecule.

Multiplying this by Avogadro’s number (N_A), which is the number of molecules in a mole, gives us the total internal energy:

\(\displaystyle U = \frac{3}{2}k_BT \times N_A \)

Boltzmann’s constant (k_B) relates to the gas constant (R) by (\(\displaystyle R = k_B \times N_A \)).

Substituting (k_B) with (R/N_A) in our equation for (U), we get:

\(\displaystyle U = \frac{3}{2}\left(\frac{R}{N_A}\right)T \times N_A \)

Simplifying, we find:

\(\displaystyle U = \frac{3}{2}RT \)

Specific Heat at Constant Volume (C_v): Using the first law of thermodynamics (where ( ∆U = Q – W), at constant volume, no work is done (∆W = 0), so (∆U = Q ).

For a temperature change of 1 unit (∆T = 1 ) and one mole of gas (m = 1), the molar specific heat at constant volume is:

\(\displaystyle C_v = \Delta U = \frac{3}{2}RT \)

Specific Heat at Constant Pressure (C_p): For an ideal gas, the difference between (C_p) and (C_v) is the gas constant (R).

Therefore, (C_p) is:

\(\displaystyle C_p = R + C_v = R + \frac{3}{2}R = \frac{5}{2}R \)

The ratio (γ) is hence:

\(\displaystyle \gamma = \frac{C_p}{C_v} = \frac{\frac{5}{2}R}{\frac{3}{2}R} = \frac{5}{3} \)

It’s fascinating to see how the simple structure of monatomic gases influences their thermal properties and how these principles apply to real-world situations.

Diatomic Gases

A molecule is a Rigid Rotator: Diatomic gases are made up of molecules with two atoms. Think of oxygen (O_₂) or nitrogen (N_₂) in our atmosphere. These molecules can move in different ways: they can translate (move from one place to another), rotate (spin around), and vibrate (atoms move back and forth). If the molecule is a rigid rotator (like (H₂), it has rotational modes contributing to its specific heat.

A Rigid Rotator is a model we use to describe the rotation of a diatomic molecule. This model assumes that the two atoms are fixed at a certain distance, like two balls connected by a stiff rod that doesn’t stretch or compress. This is a good approximation because, in reality, even though the molecule vibrates as it rotates, the bond length changes very little compared to the overall size of the molecule.

We say ‘rigid’ because we’re ignoring any stretching or bending of the bond between the two atoms when they rotate. It’s like spinning a barbell: no matter how fast you spin it, the weights at the ends don’t get any closer or farther apart.

When a diatomic molecule rotates, it has rotational energy. This energy depends on how fast it’s spinning and the distance between the atoms. The rotational energy levels of a rigid rotator are quantized, which means the molecule can only spin at certain speeds, not just any speed.

Degrees of Freedom: These molecules have five degrees of freedom: three translational (moving through space) and two rotational (spinning around two axes). Since they’re rigid, they don’t have vibrational degrees of freedom at lower energies because the atoms are fixed in place.

According to the Law of Equipartition of Energy, each degree of freedom contributes an equal amount of energy, given by (\(\displaystyle \frac{1}{2}k_BT \)), where (k_B) is Boltzmann’s constant and (T) is the temperature.

For diatomic gases, with five degrees of freedom, the internal energy (U) per molecule is:

\(\displaystyle U = \frac{5}{2}k_BT \)

To find the total internal energy for one mole of gas, we multiply by Avogadro’s number (N_A):

\(\displaystyle U = \frac{5}{2}k_BT \times N_A \)

Since (\(\displaystyle k_B \times N_A = R \)) (the gas constant), we get:

\(\displaystyle U = \frac{5}{2}RT \)

Specific Heat at Constant Volume (C_v): The molar specific heat at constant volume for a diatomic gas is:

\(\displaystyle C_v = \frac{5}{2}R \)

Specific Heat at Constant Pressure (C_p): At constant pressure, the specific heat is higher because work is done by the gas when it expands. So, (C_p) is:

\(\displaystyle C_p = \frac{7}{2}R \)

The ratio of (C_p) to (C_v) (γ): The ratio of the specific heats (γ) is:

\(\displaystyle \gamma = \frac{C_p}{C_v} = \frac{\frac{7}{2}R}{\frac{5}{2}R} = \frac{7}{5} \)

γ is the ratio of (C_p) to (C_v), which is 7:5 for diatomic gases treated as rigid rotators.

A molecule is NOT a Rigid Rotator: In a rigid rotator model, we assume that the two atoms in a diatomic molecule are fixed and do not vibrate. However, this is an approximation. In reality, the atoms in a diatomic molecule can vibrate – they can move closer together and farther apart, even as they rotate.

Degrees of Freedom: A non-rigid rotator diatomic molecule has more degrees of freedom than a rigid one. In addition to the translational and rotational movements, there are vibrational movements. These additional degrees of freedom mean that the molecule can absorb more energy without necessarily increasing its temperature as much as a rigid rotator would.

Internal Energy and Specific Heat: The internal energy of a diatomic gas that is not a rigid rotator includes not only translational and rotational energy but also vibrational energy. This means that the specific heat capacities at constant volume (C_v) and constant pressure (C_p) will be higher than for a rigid rotator because more energy is needed to raise the temperature by the same amount.

Vibrational Energy: At room temperature, many diatomic gases do not have enough energy to excite vibrational modes. However, at higher temperatures, these vibrational modes become more accessible. When these vibrational modes are excited, the specific heat capacity increases because the gas can store more energy in these vibrations.

If the molecule is not a rigid rotator (like (CO₂), it has vibrational modes that also contribute to its specific heat.

Calculating Internal Energy (U): With the additional vibrational degree of freedom, the internal energy calculation changes. Now, each molecule has (\(\displaystyle \frac{5}{2}k_BT \)) from translational and rotational motion, plus (k_BT ) from vibrational motion.

For one mole of gas, the total internal energy is:

\(\displaystyle U = \left[\frac{5}{2}k_BT + k_BT\right] \times N_A \)

Substituting (\(\displaystyle k_B \times N_A \)) with (R), we get:

\(\displaystyle U = \frac{7}{2}RT \)

Specific Heat at Constant Volume (C_v): The molar-specific heat at constant volume now accounts for the vibrational energy:

\(\displaystyle C_v = \frac{7}{2}R \)

Specific Heat at Constant Pressure (C_p): At constant pressure, the gas does work when it expands, so (C_p) is higher:

\(\displaystyle C_p = \frac{9}{2}R \)

The ratio of (C_p) to (C_v) (γ): The ratio of the specific heats (γ) is:

\(\displaystyle \gamma = \frac{C_p}{C_v} = \frac{\frac{9}{2}R}{\frac{7}{2}R} = \frac{9}{7} \)

The ratio of (C_p) to (C_v), is 9:7 for diatomic gases that are not rigid rotators.

Polyatomic Gases

The specific heat capacity of polyatomic gases is a measure of how much heat these gases can absorb before their temperature rises. Due to their complex structures, they have higher specific heat capacities, which makes them quite efficient at storing thermal energy.

Polyatomic gases are made up of molecules with three or more atoms, like carbon dioxide (CO₂) or methane (CH₄). Unlike monatomic or diatomic gases, polyatomic gases have more complex movements. They can translate, rotate, and vibrate in multiple ways because they have more atoms connected in various configurations.

Degrees of Freedom: Each type of movement (translational, rotational, vibrational) is called a degree of freedom, and each degree of freedom can store thermal energy. Polyatomic gases have more degrees of freedom than monoatomic or diatomic gases, which means they can store more heat energy without a significant change in temperature.

The specific heat capacity of polyatomic gases is the amount of heat required to raise the temperature of a unit mass of the gas by one degree Celsius (or one Kelvin). Because of their extra degrees of freedom, polyatomic gases generally have higher specific heat capacities than monatomic or diatomic gases.

When we heat a polyatomic gas, the energy doesn’t just go into making the gas move faster (translational kinetic energy). It also goes into rotational and vibrational energy. This means that for the same amount of heat added, the temperature of a polyatomic gas will increase less compared to a monatomic or diatomic gas because the energy is spread out over more degrees of freedom.

Understanding the specific heat capacity of polyatomic gases is important for many applications, such as climate modeling (where greenhouse gases play a role) and industrial processes (like chemical manufacturing).

Polyatomic Gases and Their Movements: Polyatomic gases consist of molecules with three or more atoms, like carbon dioxide (CO_₂) or methane (CH_₄). These molecules have more complex movements compared to monatomic or diatomic gases. They can move through space (translational), spin (rotational), and have their atoms move back and forth relative to each other (vibrational).

Degrees of Freedom: For polyatomic gases, there are 3 translational degrees of freedom (moving in 3D space), 3 rotational degrees (spinning around three axes), and (f) vibrational degrees (where (f) depends on the number of atoms in the molecule).

The law of Equipartition of Energy states that each degree of freedom contributes an equal amount of energy, given by ( \(\displaystyle\frac{1}{2}k_BT \)). For polyatomic gases, we sum up the energy for all degrees of freedom to get the internal energy (U):

\(\displaystyle U = \left[\frac{3}{2}k_BT + \frac{3}{2}k_BT + f \cdot k_BT\right] \times N_A \)

Replacing (\(\displaystyle k_B \times N_A \)) with (R) (the gas constant), the internal energy for one mole becomes:

\(\displaystyle U = (3 + f)RT \)

The molar specific heat at constant volume (C_v) for polyatomic gases includes all types of motion:

\(\displaystyle C_v = (3+f)R \)

At constant pressure (C_p), the specific heat is higher because the gas does work when it expands:

\(\displaystyle C_p = (5+f)R \)

Specific Heat Capacity of Polyatomic Gases measures of how much heat these gases can absorb before their temperature rises, considering all their degrees of freedom. It includes energy from translational, rotational, and vibrational motion. These are the specific heats at constant volume and pressure, respectively, and they depend on the number of vibrational modes (f).

Specific Heat Capacity of Solids

Specific heat capacity is a property that tells us how much heat energy is needed to raise the temperature of a substance. For solids, it’s the amount of heat required to raise the temperature of a certain mass of the solid by one degree Celsius (or one Kelvin).

In solids, specific heat capacity is influenced by lattice vibrations and the structure of the solid. Solids have a fixed, closely packed structure. This structure affects how they absorb and transfer heat. The specific heat capacity of a solid depends on its material properties, like the type of atoms, the arrangement of atoms, and the strength of the bonds between them.

Imagine you have a piece of metal and a piece of wood. If you put them both in the sun, the metal feels hotter much faster than the wood. That’s because metals generally have a lower specific heat capacity than wood, meaning they need less heat to increase their temperature.

Knowing the specific heat capacity of solids is important in many areas, like engineering, where materials are chosen based on how they handle heat. It’s also crucial in everyday life, like in cooking, where the specific heat capacity of cookware materials affects how food is cooked.

The Law of Equipartition of Energy states that each degree of freedom (movement option) of a particle has an average energy of (\(\displaystyle \frac{1}{2}k_BT \)).

In three dimensions, an atom has three degrees of freedom for movement, and since it oscillates back and forth, we count each dimension twice, leading to (\(\displaystyle 3 \times 2 \times \frac{1}{2}k_BT = 3k_BT \)) of energy per atom.

For a mole of solid, which contains Avogadro’s number (N_A) of atoms, the total internal energy (U) is:

\(\displaystyle U = 3k_BT \times N_A \)

Replacing (\(\displaystyle k_B \times N_A \)) with (R) (the gas constant), we get:

\(\displaystyle U = 3RT \)

Molar Specific Heat Capacity at Constant Pressure: If the pressure is constant and the solid doesn’t expand much (which is typical for solids), the change in volume (∆V) is nearly zero. So, the heat added (∆Q) is equal to the change in internal energy (∆U), and we can say:

\(\displaystyle \Delta Q = \Delta U \)

The molar specific heat capacity (C) to change the temperature by 1 unit is then:

\(\displaystyle C = 3R \)

Specific heat capacity of solids is required to raise the temperature of a solid by a certain amount. Internal energy includes the oscillation energy of atoms in the solid. Molar specific heat capacity is (3R) for solids, reflecting the energy stored in the oscillations of atoms.

How does the specific heat capacity of metals compare to that of insulators?

The specific heat capacity of metals generally differs from that of insulators, and here’s how:

Metals: Metals typically have a lower specific heat capacity compared to insulators. This means they require less heat energy to raise their temperature by 1 degree Celsius (or 1 Kelvin). Metals are good conductors of heat, so they tend to heat up and cool down quickly.

Insulators: Insulators, on the other hand, have a higher specific heat capacity. They absorb more heat before their temperature starts to rise significantly. Insulators are poor conductors of heat, which means they respond slowly to changes in temperature and are used to keep heat in or out.

The difference in specific heat capacities is due to the material’s atomic and molecular structures. Metals, with their free electrons, can transfer energy quickly, while insulators, with more complex molecular structures, tend to ‘trap’ heat in various vibrational and rotational modes. In practical terms, this is why metals feel colder on a chilly day and hotter on a warm day compared to insulators like wood or plastic.

Specific Heat Capacity of Water

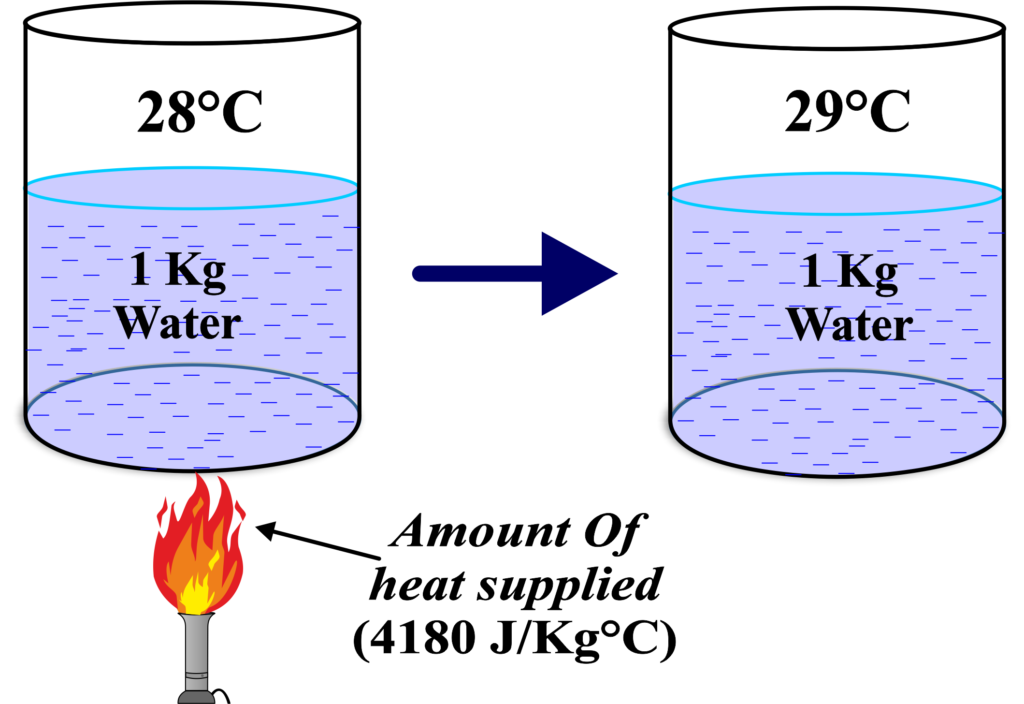
Specific heat capacity is a measure of how much heat energy is needed to raise the temperature of a substance. For water, it’s the amount of heat required to raise the temperature of a certain mass of water by one degree Celsius (or one Kelvin). Water has a high specific heat capacity of approximately 4.18 J/g°C, which means it can absorb a lot of heat before it gets hot.

Water has a high specific heat capacity, which means it can absorb a lot of heat before it gets hot. This property is due to the hydrogen bonds between water molecules, which need a significant amount of energy to break.

Water’s high specific heat capacity is crucial for regulating the Earth’s climate. It allows oceans to absorb large amounts of heat without a significant increase in temperature. It also makes water an excellent coolant for industrial processes and in-car radiators.

A water molecule is made up of three atoms: two hydrogen (H) atoms and one oxygen (O) atom. This triatomic structure gives water its unique properties.

Internal Energy (U): The internal energy of a substance is the total energy of all its molecules. For water, we consider the kinetic energy due to the movement of the molecules and the potential energy from the forces between them.

Each atom contributes to the internal energy through translational, rotational, and vibrational motion. Since a water molecule has three atoms, and each atom can move in three dimensions, we multiply by three for the translational motion:

\(\displaystyle U = 3 \times 3k_BT \times N_A \)

Simplifying, we get:

\(\displaystyle U = 9k_BT \times N_A \)

Since (R) (the gas constant) is equal to (\(\displaystyle k_B \times N_A \)), we can substitute (\(\displaystyle k_B \times N_A \)) with (R) to find the internal energy for one mole of water:

\(\displaystyle U = 9RT \)

The specific heat capacity at constant volume (C_v) for water can be derived from the internal energy. It’s the amount of heat required to raise the temperature of one mole of water by one degree Celsius:

\(\displaystyle C_v = \frac{\Delta U}{n\Delta T} \)

Since (∆U) for one mole (n = 1) and a temperature change of 1 degree (∆T = 1) is (9R), we have:

\(\displaystyle C_v = 9R \)

The value (9R) is a theoretical calculation based on treating water as a solid. In reality, water’s specific heat capacity is influenced by its liquid state and the hydrogen bonding between molecules.

The actual specific heat capacity of water is approximately (\(\displaystyle 4.18 \frac{J}{g°C}\) ) or (\(\displaystyle 4180 \frac{J}{kg°C} \)), which is quite high compared to many other substances. This high value is due to the strong hydrogen bonds that require more energy to break.

Why does water have such a high specific heat capacity?

Hydrogen Bonds in Water: Water molecules are polar, meaning they have a positive end and a negative end. The positive end is the hydrogen atoms, and the negative end is the oxygen atom. These polar ends allow water molecules to form hydrogen bonds with each other.

When water absorbs heat, these hydrogen bonds must be broken for the water molecules to move more freely and the temperature to rise. Breaking these bonds requires a significant amount of energy.

Conversely, when water cools down and the temperature decreases, hydrogen bonds form again, releasing a considerable amount of energy.

Because of these hydrogen bonds, water can absorb more heat before increasing in temperature compared to many other substances. This property allows water to regulate temperature in the environment and living organisms effectively.

So, the strong hydrogen bonds in water require more energy to overcome, leading to water’s high specific heat capacity. It’s one of the reasons why water is such a vital component of Earth’s climate system and why it’s used widely as a coolant in various technologies.

Uses of Specific Heat Capacity

Specific heat capacity is a property that plays a crucial role in various aspects of science and everyday life.

Climate Regulation: Water has a high specific heat capacity, which allows large bodies of water like oceans to absorb and store vast amounts of heat. This helps to regulate the Earth’s climate by moderating temperature changes.

Cooking: The specific heat capacity of materials determines how they are used in cooking. For example, metals with low specific heat capacities are used for frying pans because they heat up quickly.

Building Materials: In the construction industry, the specific heat capacities of materials affect how buildings respond to temperature changes. Materials with high specific heat capacity can help keep buildings cool in hot climates.

Thermal Insulators: Materials with high specific heat capacity are used as insulators. They can help maintain a consistent temperature in space by absorbing heat when the surroundings are hot and releasing it when it’s cooler.

Industrial Processes: In industries, specific heat capacity is important for designing systems that involve heating or cooling substances, such as chemical reactors and heat exchangers.

Thermal Comfort: Clothing and bedding materials are chosen based on their specific heat capacities to provide comfort in different temperatures.

Energy Storage: Substances with high specific heat capacities can be used in thermal energy storage systems to store excess heat, which can be used later when needed.

Understanding the specific heat capacity of substances helps us predict how they will behave in different thermal environments and is essential for various applications ranging from environmental science to culinary arts and engineering.

Also Read: Kinetic Theory of Gases

Solved Examples

Problem 1: A 2 kg block of aluminum (specific heat capacity (c = 900 J/kg.K) is heated from ( 25^∘C) to ( 75^∘C). Calculate the amount of heat energy required.

Solution: The amount of heat energy (Q) required to raise the temperature of a mass (m) by (∆T) is given by:

\(\displaystyle Q = mc\Delta T \)

Given: Temperature change (∆T = 75 – 25 = 50 K)

Calculate (Q):

\(\displaystyle Q = 2 \times 900 \times 50 \)
\(\displaystyle Q = 90,000 \, \text{J} \)

Therefore, the amount of heat energy required is ( 90,000 J).

Problem 2: Calculate the molar specific heat at constant volume (C_V) for a monatomic ideal gas. Given the universal gas constant ( R = 8.314 J/mol.K).

Solution: For a monatomic ideal gas, the molar specific heat at constant volume (C_V) is given by:

\(\displaystyle C_V = \frac{3}{2} R \)

Calculate (C_V):

\(\displaystyle C_V = \frac{3}{2} \times 8.314 \)
\(\displaystyle C_V = 12.471 \, \text{J/mol} \cdot \text{K} \)

Therefore, the molar specific heat at constant volume for a monatomic ideal gas is (12.471 J/mol.K).

Problem 3: How much heat is needed to raise the temperature of 500 g of water from (20^∘ C) to ( 80^∘C)? The specific heat capacity of water is ( 4.18 J/g.K).

Solution: Temperature change (∆T = 80 – 20 = 60K)

Calculate (Q):

\(\displaystyle Q = mc\Delta T \)
\(\displaystyle Q = 500 \times 4.18 \times 60 \)
\(\displaystyle Q = 125,400 \, \text{J} \)

Therefore, the heat needed is (125,400 J).

Problem 4: Calculate the molar specific heat at constant pressure (C_P) for a diatomic ideal gas. Given the universal gas constant ( R = 8.314 J/mol.K).

Solution: For a diatomic ideal gas, the molar specific heat at constant pressure (C_P) is given by:

\(\displaystyle C_P = \frac{7}{2} R \)

Calculate (C_P):

\(\displaystyle C_P = \frac{7}{2} \times 8.314 \)
\(\displaystyle C_P = 29.099 \, \text{J/mol} \cdot \text{K} \)

Therefore, the molar specific heat at constant pressure for a diatomic ideal gas is (29.099 J/mol.K).

Problem 5: A sample of (2 mol) of a polyatomic ideal gas (with (C_V = 3R) is heated at constant volume from (300 K) to (600 K). Calculate the heat energy supplied.

Solution: The heat energy (Q) required to raise the temperature of (n) moles of gas at constant volume is given by:

\(\displaystyle Q = nC_V\Delta T \)

Given: Temperature change (∆T = 600 – 300 = 300 K)

Calculate (Q):

\(\displaystyle Q = 2 \times 3 \times 8.314 \times 300 \)
\(\displaystyle Q = 2 \times 3 \times 8.314 \times 300 \)
\(\displaystyle Q = 14,965.2 \, \text{J} \)

Therefore, the heat energy supplied is (14,965.2 J).

Problem 6: A 500 g iron rod is heated from ( 25^∘C) to ( 75^∘C). If the specific heat capacity of iron is ( 450 J/kg.K), calculate the heat absorbed by the iron rod.

Solution: Calculate (Q),

\(\displaystyle Q = mc\Delta T \)
\(\displaystyle Q = 0.5 \times 450 \times 50 \)
\(\displaystyle Q = 11,250 \, \text{J} \)

Therefore, the heat absorbed by the iron rod is ( 11,250 J).

FAQs