Stokes’ law

Imagine it’s the mid-19th century, and scientists are fascinated by how things move in fluids. This is where Sir George Gabriel Stokes, a brilliant British scientist, steps into the picture. In 1851, Stokes was pondering over the movement of tiny particles in fluids. He noticed that small things like pollen grains didn’t just zip through water; they seemed to slow down as if the water was holding them back.

Stokes realized that this “holding back” was due to the fluid’s viscosity, which is just a fancy word for “thickness” or “stickiness”. Think of it like trying to walk through a room filled with honey versus a room filled with air. The honey room would slow you down a lot more, right? That’s viscosity in action!

So, Stokes started doing experiments and came up with a law that could predict how fast these small particles would fall in a fluid. He found out that the slower fall wasn’t just because of the fluid’s viscosity, but also the size of the particles and how fast they were moving to begin with.

His work was groundbreaking because it helped people understand not just why some things fall slowly in liquids, but also how to measure the viscosity of the liquid itself. And guess what? The unit of measurement for viscosity is even named after him – the stoke!

Stokes’ Law is super important because it’s used in all sorts of real-life applications, from figuring out how to separate oil from water to understanding how blood flows in our bodies. All of this came from Stokes’ curiosity about the world around him and his dedication to figuring out the rules that govern how things move in fluids.

What is Stokes’ Law?

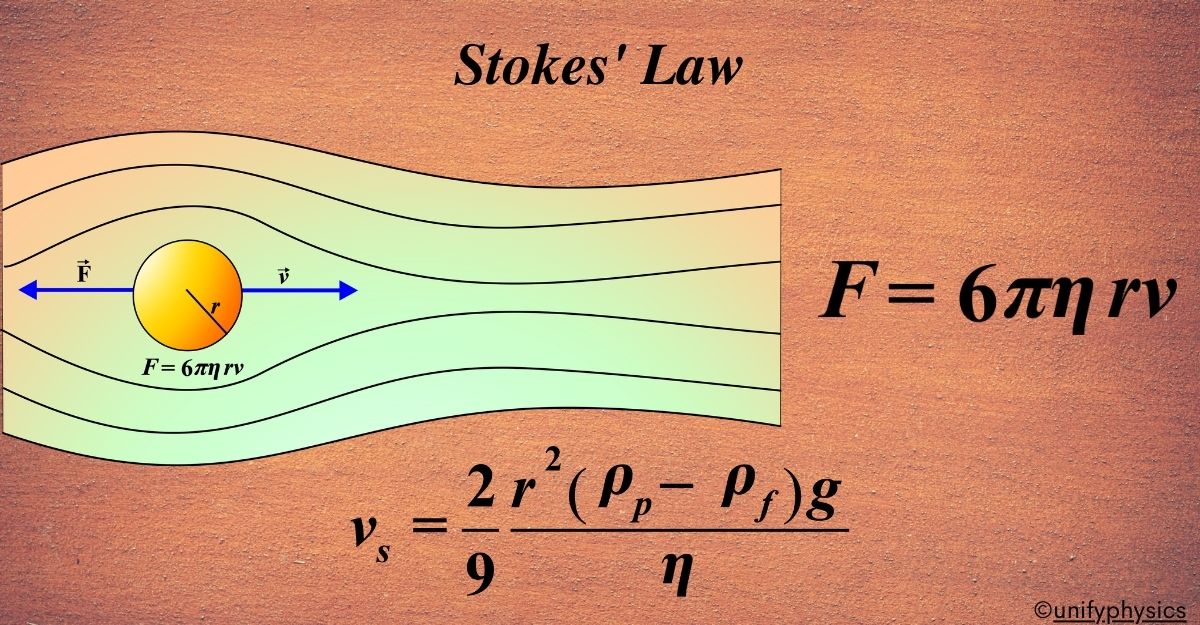
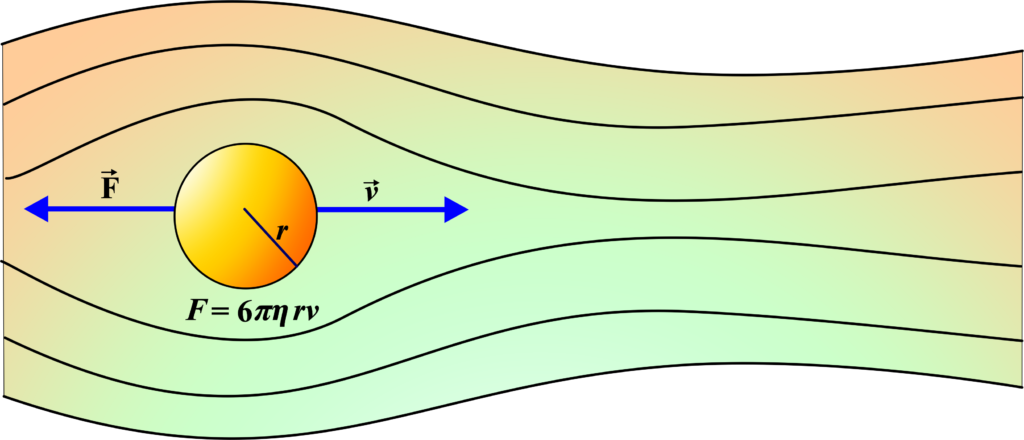
Stokes’ Law states that the drag force acting on a spherical object moving through a viscous fluid is directly proportional to the velocity of the object, the radius of the object, and the viscosity of the fluid.

Stokes’ Law describes the force of friction that acts on spherical objects when they move through a viscous fluid. It’s like how a ball falls slower through honey than through water because honey is thicker.

Imagine you have a tiny, smooth ball, and you drop it into a jar of syrup. You’ll notice that it doesn’t fall straight down like it would in the air; it takes its sweet time (pun intended). This slow motion is because the syrup is viscous, which means it’s thick and sticky, and it resists the movement of the ball.

Now, Stokes’ Law is like a recipe that tells us how to calculate the force that this syrup exerts on the ball to slow it down. This force is called the drag force, and it’s important because it tells us how fast the ball will eventually fall through the syrup without speeding up or slowing down anymore.

• The drag force is directly proportional to the syrup’s stickiness (viscosity), the size of the ball (its radius), and how fast the ball is trying to move (its velocity).

In other words, if you have a bigger ball, or if the syrup is stickier, or if you try to push the ball faster, the drag force will be stronger, and the ball will move slower.

So, Stokes’ Law helps us understand the motion of small objects in fluids, and it’s super useful in many areas of science and engineering, like designing equipment that needs to work with fluids, understanding natural phenomena, and even in medicine!

Stokes Law Formula

Imagine you’re playing with marbles in a pool of water. If you gently drop a marble into the water, it doesn’t sink straight down quickly; it takes its time, right? That’s because the water is pushing against the marble, trying to slow it down. This push is what we call the drag force, and Stokes’ Law gives us a way to calculate it. The formula looks like this:

\(\displaystyle\begin{equation}\label{eqn:1}\boxed{\boldsymbol{ F = 6 \pi \eta r v }} \end{equation}\)

• (F) is the drag force, which is the push from the water on the marble.
• (η) is the viscosity of the water, which tells us how thick or syrupy the water is.
• (r) is the radius of the marble, so a bigger marble feels a bigger push.
• (v) is the velocity of the marble as it sinks.

So, according to this formula, if the water is thicker (like honey), or if the marble is bigger, or if you try to push the marble down faster, the drag force will be greater.

Dimensional Formula: Now, let’s talk about the dimensional formula. This is like a secret code that tells us the type of physical quantity we’re dealing with, whether it’s length, mass, time, or a combination of these.

For the drag force (F), the dimensional formula is:

\(\displaystyle [F] = [MLT^{-2}] \)

When we look at the formula \(\displaystyle F = 6 \pi \eta r v \), we can break it down into dimensions too:

• (η) has dimensions of \(\displaystyle [ML^{-1}T^{-1}] \) (mass per length per time),
• (r) has dimensions of [L] (length),
• (v) has dimensions of [LT^-1] (length per time).

Putting it all together, the drag force (F) combines these dimensions to give us [MLT^-2], which matches the dimensions of force!

Conditions For Stokes’ Law

To make sure that Stokes’ Law can predict the drag force accurately, certain conditions must be met. Think of these conditions as the “rules of the game” for Stokes’ Law to work properly.

• Spherical Shape: The object falling through the fluid must be a perfect sphere, like a marble or a ball bearing. This is because Stokes’ Law is based on the math for spheres, and if the shape is different, the math gets way more complicated.
• Smooth Surface: The sphere should be as smooth as glass. Any roughness can change the way the fluid flows around the object, which would mess up our calculations.
• Uniform Density: The sphere needs to have the same density all the way through. If it’s denser in some parts than others, it won’t fall evenly, and again, our predictions would be off.
• Size Matters: The sphere should be small, but not too small. It should be much larger than the fluid’s molecules, but still small enough that it doesn’t cause any wild movements in the fluid.
• Laminar Flow: The fluid flow around the sphere must be smooth and orderly, which is called laminar flow. If the flow gets chaotic and turbulent, Stokes’ Law won’t apply.
• No Interference: The spheres shouldn’t be affecting each other’s movement. This means they need to be spaced far enough apart so they’re not bumping into each other or changing the way the fluid moves around them.
• Infinite Fluid: The fluid should extend infinitely in all directions. In real life, this isn’t possible, but we assume this to simplify the situation. It means the sphere shouldn’t be near walls or the bottom of the container, which could affect its fall.
• Slow Movement: The sphere must move slowly through the fluid. If it’s moving too fast, the conditions change, and Stokes’ Law won’t be accurate.

When all these conditions are just right, Stokes’ Law can tell us exactly how the fluid’s viscosity will slow down the sphere as it falls. It’s like having the perfect conditions for a game of marbles – if the ground is too bumpy or sloped, the game won’t work as expected. Similarly, for Stokes’ Law to work, we need the perfect “playing field” for our little spherical objects.

Stokes’ Law Derivation

To derive Stokes’ Law, we’ll start with the basic understanding that when a sphere moves through a viscous fluid, it experiences a drag force due to the fluid’s viscosity. This force opposes the sphere’s motion and is proportional to the sphere’s velocity, the fluid’s viscosity, and the sphere’s radius.

We begin with the assumption that the drag force (F) is directly proportional to the velocity of the sphere (v), the viscosity of the fluid (η), and the radius of the sphere (r). Mathematically, we express this as:

\(\displaystyle F \propto \eta r v \)

To convert this proportionality into an equation, we introduce a constant of proportionality, which we’ll call (k). The equation now looks like this:

\(\displaystyle F = k \eta r v \)

We use dimensional analysis to determine the value of (k). The dimensions of force are [MLT^-2] , and by equating the dimensions on both sides of the equation, we can solve for (k).

We know that the dimensions of viscosity (η) are [ML^-1T^-1] , the radius (r) has dimensions of [L], and the velocity (v) has dimensions of [LT^-1]. So, our equation in terms of dimensions is:

\(\displaystyle [MLT^{-2}] = k [ML^{-1}T^{-1}] [L] [LT^{-1}] \)

When we simplify the equation, we find that (k) must be dimensionless and have a value that makes the equation dimensionally consistent. Through experimental determination, Stokes found that (k) equals \(\displaystyle 6\pi \).

With the value of (k) determined, we arrive at the final form of Stokes’ Law:

\(\displaystyle F = 6\pi \eta r v \)

This equation tells us the drag force experienced by a sphere moving through a viscous fluid. It’s a fundamental result in fluid dynamics and helps us understand how objects move through fluids in many practical situations.

Terminal Velocity

Terminal velocity is the constant speed that a freely falling object eventually reaches when the resistance of the medium prevents further acceleration. In the context of Stokes’ Law, it’s when the frictional force equals the gravitational force, and the object falls at a steady rate.

When you drop a small ball in a jar of honey, initially, it starts to accelerate due to gravity. But very quickly, you’ll notice it stops speeding up and starts to fall at a steady speed. This steady speed is what we call the terminal velocity.

Now, why does this happen? As the ball speeds up, the drag force (which is the force the honey exerts to slow the ball down) increases. Eventually, this drag force becomes equal to the gravitational force pulling the ball down. When these two forces balance out, the net force on the ball becomes zero, and it stops accelerating. From this point on, the ball continues to fall at a constant speed, which is the terminal velocity.

Stokes’ Law helps us calculate this terminal velocity for small spherical objects in a viscous fluid. According to Stokes’ Law, the drag force (F) is given by:

\(\displaystyle F = 6\pi\eta rv \)

Here, (η) is the fluid’s viscosity, (r) is the radius of the sphere, and (v) is the velocity of the sphere.

At terminal velocity, the drag force (F) equals the gravitational force minus the buoyant force (which is the force due to the fluid displaced by the sphere). So, we can set up the equation:

\(\displaystyle 6\pi\eta rv = mg – \rho_{\text{fluid}} Vg \)

Where (m) is the mass of the sphere, (g) is the acceleration due to gravity, (ρ_fluid) is the density of the fluid, and (V) is the volume of the sphere.

From this equation, we can solve for the terminal velocity (v), which tells us how fast the sphere will fall through the fluid without accelerating further.

In simple terms, Stokes’ Law in the context of terminal velocity is all about finding that sweet spot where a sphere falls through a fluid at a constant speed because the forces of drag and gravity are perfectly balanced.

Settling Velocity

Settling velocity is typically used in the context of particles in a fluid, especially in sedimentation processes. It refers to the constant speed at which a particle settles or falls through a fluid, reaching a balance between gravitational forces and the resistance due to the fluid’s viscosity.

Imagine you’re at a beach, and you drop a small pebble into the water. You’ll notice that it doesn’t just zoom down to the bottom like it would if you dropped it in the air. Instead, it falls more slowly, right? This is because the water is resisting its fall. Now, the speed at which the pebble falls through the water without getting any faster or slower is what we call the settling velocity.

• When the pebble first hits the water, gravity pulls it down, making it accelerate.
• As it speeds up, the water pushes back against it more and more. This pushback is called the drag force.
• Eventually, the pebble reaches a speed where the drag force is just as strong as the pull of gravity. When these two forces balance out, the pebble stops accelerating and moves at a constant speed. This is the settling velocity.

Now, let’s connect this to Stokes’ Law. Stokes’ Law tells us how to calculate the drag force on small, spherical objects moving through a fluid like water or air. The law says that the drag force depends on the fluid’s viscosity (how thick or syrupy it is), the radius of the object, and the object’s velocity.

Using Stokes’ Law, we can calculate the settling velocity by setting the drag force equal to the gravitational force (minus any buoyant force if the object is in a liquid). The formula looks like this:

\(\displaystyle F_{\text{drag}} = 6\pi \eta r v_{\text{settling}} \)
\(\displaystyle F_{\text{gravity}} = mg \)

At settling velocity, \(\displaystyle F_{\text{drag}} = F_{\text{gravity}} \), so we can solve for (v_settling).

The settling velocity is the steady speed that an object reaches as it falls through a fluid, where the upward drag force due to the fluid’s viscosity balances the downward gravitational force.

Settling Velocity Derivation (spherical particle in a fluid)

Settling velocity is the constant speed achieved by a particle as it falls through a fluid, where the forces of gravity and the drag force due to the fluid’s viscosity are balanced.

When a particle falls through a fluid, it experiences two main forces:

• Gravitational force (F_g): pulling it downwards.
• Buoyant force (F_b): an upward force due to the displaced fluid.
• Drag force (F_d): an upward force opposing the motion due to the fluid’s viscosity.

The gravitational force is given by:

\(\displaystyle F_g = m_p g \)

where (m_p) is the mass of the particle and (g) is the acceleration due to gravity.

According to Archimedes’ principle, the buoyant force is equal to the weight of the fluid displaced by the particle:

\(\displaystyle F_b = \rho_f V_p g \)

where (ρ_f) is the density of the fluid and (V_p) is the volume of the particle.

Stokes’ Law gives us the drag force for a sphere moving at low Reynolds number (laminar flow) as:

\(\displaystyle F_d = 6\pi \eta r v_s \)

where (η) is the viscosity of the fluid, (r) is the radius of the particle, and (v_s) is the settling velocity.

At settling velocity, the sum of the buoyant force and the drag force equals the gravitational force:

\(\displaystyle F_b + F_d = F_g \)

Substituting the expressions for (F_b), (F_d), and (F_g) into the equilibrium condition, we get:

\(\displaystyle \rho_f V_p g + 6\pi \eta r v_s = m_p g \)

The mass of the particle can be expressed in terms of its density (ρ_p) and volume (V_p):

\(\displaystyle m_p = \rho_p V_p \)

Substituting (m_p) into the equilibrium condition and simplifying, we get:

\(\displaystyle \rho_f V_p g + 6\pi \eta r v_s = \rho_p V_p g \)

Rearrange the equation to solve for the settling velocity (v_s):

$$ v_s = \frac{(\rho_p – \rho_f) V_p g}{6\pi \eta r} $$

The volume of a spherical particle is:

\(\displaystyle V_p = \frac{4}{3}\pi r^3 \)

Substitute (V_p) into the equation for (v_s) and simplify:

\(\displaystyle\begin{equation}\label{eqn:2}\boxed{\boldsymbol{ v_s = \frac{2}{9}\frac{r^2 (\rho_p – \rho_f) g}{\eta} }} \end{equation}\)

And there we have it, the derived expression for the settling velocity of a spherical particle in a fluid. This formula shows that the settling velocity is directly proportional to the square of the particle’s radius, the difference in density between the particle and the fluid, and the acceleration due to gravity, and is inversely proportional to the fluid’s viscosity.

Also Read: Pascal’s law

Limitations of Stoke’s Law

Stokes’ Law is super helpful for predicting how spheres move in a fluid, but it doesn’t work in every situation. Here are some of the limitations:

Shape Matters: Stokes’ Law assumes that particles are perfectly spherical. In real life, particles can be all sorts of shapes, and if they’re not spherical, the law doesn’t apply.

Size Limitations: The law is meant for small particles, but not too small. If particles are too big, they can cause turbulence as they move through the fluid, and if they’re too small, they’re affected by Brownian motion (random movement of particles).

Smooth and Solid: The particles need to have a smooth surface and be solid. If they’re rough or squishy, the fluid will interact with them differently, and Stokes’ Law won’t be accurate.

Laminar Flow Only: The fluid flow around the particle must be smooth, which is called laminar flow. If the flow is turbulent (chaotic), then Stokes’ Law doesn’t work.

No Interactions: Stokes’ Law assumes that particles don’t affect each other’s movement. But in reality, particles can clump together or push each other around, especially if there are lots of them.

Uniform Fluid: The law assumes that the fluid is infinite and the same everywhere. But if there are variations in the fluid, like temperature or density changes, the law won’t be precise.

Slow Motion: Stokes’ Law applies to particles moving slowly through the fluid. If they’re moving fast, the conditions change, and the law won’t give the right answers.

Applications of Stoke’s Law in Real Life

Stokes’ Law isn’t just a theory; it has many practical uses in our daily lives and various scientific fields. Here are some examples:

• Settling of Particles: In water treatment plants, Stokes’ Law is used to design sedimentation tanks. These tanks help in separating out particles from water by allowing them to settle at the bottom, based on their size and the fluid’s viscosity.
• Formation of Raindrops: Ever wonder how raindrops form? Small water droplets in clouds have low terminal velocities, so they don’t fall right away. As they combine and grow, their terminal velocities increase, and eventually, they fall as rain. Stokes’ Law helps explain this process.
• Blood Tests: In medicine, Stokes’ Law is used in blood tests to measure the rate at which red blood cells settle in a test tube, which can indicate certain health conditions.
• Airborne Particles: Environmental scientists use Stokes’ Law to study the behavior of small particles in the atmosphere, like dust or pollutants, and how they settle.
• Sports Equipment Design: The drag force calculated by Stokes’ Law is important in designing sports equipment like golf balls or baseballs to optimize their performance in the air.
• Underwater Vehicles: Engineers use Stokes’ Law to design underwater vehicles, ensuring they can move efficiently through water.
• Parachutes: When a person jumps with a parachute, they reach a terminal velocity where the air resistance balances the gravitational pull, allowing for a safe descent. Stokes’ Law helps in understanding and calculating this terminal velocity.
• Oil Exploration: In the oil industry, Stokes’ Law is applied to separate drilling mud from valuable materials during the drilling process.

Solved Examples

Example 1: A spherical object with a radius of (0.05 m) and a density of (900 kg/m³) falls through a fluid with a viscosity of (0.002 Ns/m²). Calculate its terminal velocity.

Solution: Using Stokes’ law, the terminal velocity (v_t) can be calculated as:

\(\displaystyle v_t = \frac{2r^2(g – g’)}{9\eta} \)

Given: r = 0.05 m; g = 9.8 m/s², g’ = 0 (as the object is falling freely); η = 0.002 Ns/m²

Substituting the values:

\(\displaystyle v_t = \frac{2 \times (0.05)^2 \times 9.8}{9 \times 0.002} \)
\(\displaystyle v_t = \frac{0.0049 \times 9.8}{0.018} \)
\(\displaystyle v_t = \frac{0.047}{0.018} \)
\(\displaystyle v_t \approx 2.61 \, \text{m/s} \)

So, the terminal velocity of the spherical object is (2.61 m/s).

Example 2: Calculate the drag force acting on a spherical object with a radius of (0.1 m) falling through a fluid with a viscosity of (0.005 Ns/m²) at a velocity of (1 m/s).

Solution: The drag force (F_d) can be calculated using Stokes’ law as:

\(\displaystyle F_d = 6\pi \eta rv \)

Given: r = 0.1 m; η = 0.005 Ns/m²; v = 1 m/s

Substituting the values:

\(\displaystyle F_d = 6\pi \times 0.005 \times 0.1 \times 1 \)
\(\displaystyle F_d = 6\pi \times 0.0005 \)
\(\displaystyle F_d \approx 0.00942 \, \text{N} \)

So, the drag force acting on the spherical object is approximately (0.00942 N).

Example 3: A spherical particle with a radius of \(\displaystyle1 \times 10^{-4} m\) and density (2650 kg/m^{3) is settling in the} water. If the viscosity of water is \(\displaystyle 1 \times 10^{-3} Pa \cdot s\), find the settling velocity.

Solution: To find the settling velocity of the spherical particle in water, we can use Stokes’ law, which relates the settling velocity to the viscosity of the fluid, the radius of the particle, and the density difference between the particle and the fluid.

Stokes’ law for settling velocity is given by:

\(\displaystyle v_s = \frac{2}{9} \frac{r^2 ( \rho_p – \rho_f ) g}{\eta} \)

Given:

• Radius of the particle (r) = \(\displaystyle 1 \times 10^{-4} \) m
• Density of the particle (ρ_p )) = (2650 ) kg/m³
• Density of water (ρ_f )) = (1000 ) kg/m³
• Viscosity of water (η) = (1 \times 10^{-3} ) Pa·s
• Acceleration due to gravity (g) = (9.8 ) m/s²

Substituting the given values into Stokes’ law:

\(\displaystyle v_s = \frac{2}{9} \frac{(1 \times 10^{-4})^2 (2650 – 1000) \times 9.8}{1 \times 10^{-3}} \)

\(\displaystyle v_s = \frac{2}{9} \frac{1 \times 10^{-8} \times 1650 \times 9.8}{1 \times 10^{-3}} \)

\(\displaystyle v_s = \frac{2}{9} \frac{16170 \times 10^{-8}}{1 \times 10^{-3}} \)

\(\displaystyle v_s = \frac{2 \times 16170}{9 \times 10^5} \)

\(\displaystyle v_s = \frac{32340}{9 \times 10^5} \)

\(\displaystyle v_s = \frac{3593.33 \times 10^{-5}}{10^5} \)

\(\displaystyle v_s = 3.59333 \times 10^{-5} \, \text{m/s} \)

So, the settling velocity of the spherical particle in water is \(\displaystyle 3.59333 \times 10^{-5} \, \text{m/s}\).

FAQs