Streamline And Turbulent Flow

The concept of streamlined flow has been around for centuries, but it began to take shape with the work of scientists and mathematicians who were curious about how fluids move. People have always been fascinated by the movement of water in rivers and the way smoke rises in the air. Early civilizations had a practical understanding of fluid flow, which was essential for agriculture and architecture.

In the Renaissance, Leonardo da Vinci made detailed observations of water flow, sketching the patterns he saw. He was one of the first to describe the smooth patterns of water flowing around obstacles, which are related to streamlines. Fast forward to the 17th century, and Isaac Newton’s laws of motion provided a foundation for understanding the forces involved in fluid movement.

The study of fluid dynamics became more formalized with the work of Daniel Bernoulli and Claude-Louis Navier. Bernoulli’s principle, which relates pressure, velocity, and height in a moving fluid, is a cornerstone of fluid mechanics.

In the late 19th century, Osborne Reynolds, a British engineer, conducted experiments that led to a deeper understanding of streamline and turbulent flow. He introduced the Reynolds number, a dimensionless quantity that predicts the type of flow based on the fluid’s properties and flow conditions.

The work of Reynolds and his contemporaries laid the foundation for the field of fluid dynamics, which is the study of fluid flow. Over time, scientists developed mathematical models and equations to describe streamlined flow and predict when a fluid would transition to turbulent flow.

What are Streamlines?

Streamlines are imaginary lines that show the path of fluid particles in a steady flow. They are drawn such that the tangent to the streamline at any point is in the direction of the fluid velocity at that point.

Imagine you’re sitting by a calm river and you drop a leaf into the water. You’ll notice that the leaf starts to follow a smooth path as it flows downstream. If you could trace the path of the leaf or any other tiny particle in the water, you’d be drawing what we call a streamline.

Streamlines are like the tracks of fluid particles in motion. They are invisible lines that show us exactly how the fluid is moving at every point. Here’s what makes them special:

• Direction: The direction of the streamline at any point is the same as the direction of the fluid’s velocity at that point. So, if you were to place a tiny arrow on a streamline, it would point in the direction the fluid is flowing.
• No Crossing: Streamlines never cross each other. If they did, it would mean the fluid would have to be moving in two different directions at the same time at that point, which is impossible!
• Steady Flow: Streamlines represent steady flow, where the pattern of the flow doesn’t change over time. Even if the fluid keeps moving, the streamlines stay the same shape.

By looking at streamlines, we can visualize the flow of a fluid. They help us see if the flow is smooth and straight or if it’s swirling around.

So, streamlines are a really useful way to picture fluid flow, especially in diagrams and simulations. They help us understand and predict how fluids will behave, which is super important in fields like engineering and meteorology.

What is Streamline Flow?

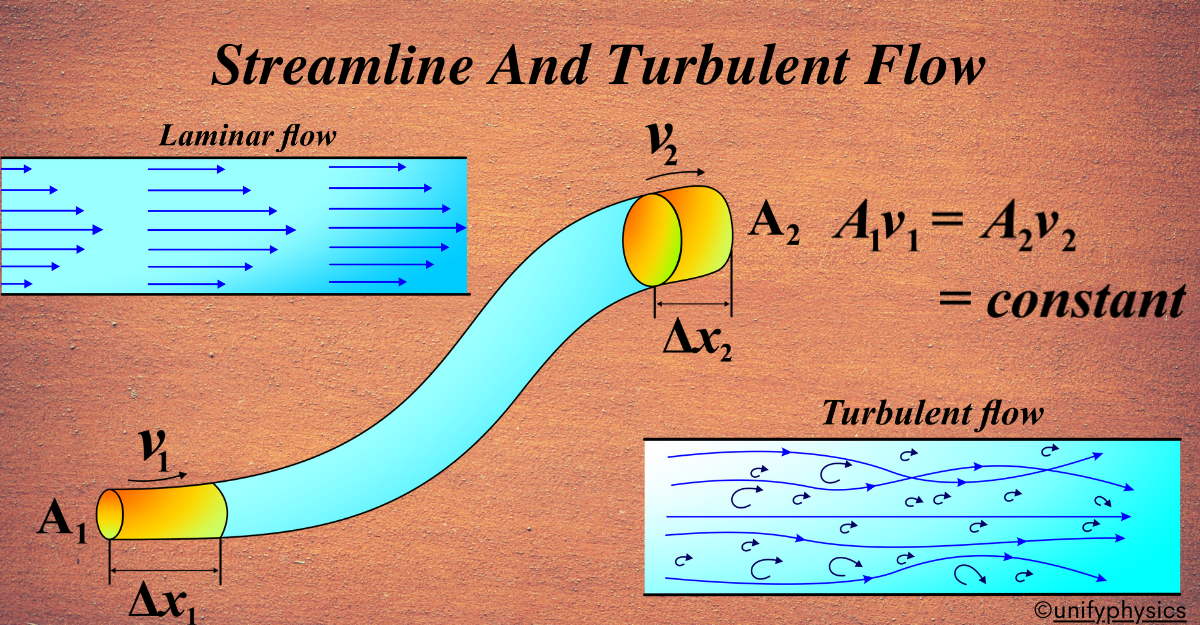
Streamline flow, or laminar flow, is a type of fluid flow where the fluid moves in parallel layers, with no disruption between the layers. The velocity of the fluid at any point is constant over time.

Streamline flow, also known as laminar flow, is a smooth pattern of fluid motion where every particle of the fluid follows a path called a streamline, and all these paths are parallel to each other. It’s like watching a group of athletes running in their lanes on a track; they don’t cross into each other’s lanes and maintain a steady pace.

Here’s what you need to know about streamline flow:

• Parallel Paths: In streamlined flow, fluid particles move in straight or gently curving paths that never intersect with one another.
• Consistent Speed: Each particle moves at a constant speed along its path. This means that if you were to watch a particle, it would keep moving steadily without speeding up or slowing down.
• Orderly Movement: There’s no mixing or swirling in streamlined flow. The fluid layers slide over one another smoothly, like sheets of paper sliding over each other.
• Predictable: Because the flow is so orderly, it’s easy to predict where a particle will go. This makes calculations and designs based on streamlined flow very reliable.
• Low Velocity: Streamline flow typically occurs at lower velocities. When the speed of the fluid increases too much, the flow can become turbulent.

In practical terms, you can think of streamlined flow as the kind of flow you see when honey pours out of a jar or when smoke rises smoothly from a candle.

Streamline Flow Equation (Equation of Continuity)

The equation of continuity states that for an incompressible fluid, the mass flow rate must remain constant from one cross-section to another.

The Equation of Continuity is a fundamental principle in fluid dynamics that applies to streamline (laminar) flow. It’s based on the conservation of mass, which tells us that fluid doesn’t just disappear or magically appear; it has to go somewhere.

\(\displaystyle\begin{equation}\label{eqn:1}\boxed{\boldsymbol{A_1 v_1 = A_2 v_2 }} \end{equation}\)

• (A) represents the cross-sectional area of the pipe or channel through which the fluid is flowing.
• (v) is the velocity of the fluid at that particular section.
• The subscripts (1) and (2) refer to two points along the flow.

It means that if you have a pipe with varying width, and fluid flows through it, the product of the area and the velocity at any two points is constant. So, if the pipe narrows down (the area gets smaller), the fluid has to speed up to keep the product the same. Conversely, if the pipe widens, the fluid slows down.

This equation helps us understand how fluids behave when they move through different shapes of pipes or channels. It’s crucial for designing systems like water supply networks, air conditioning ducts, and even for understanding blood flow in arteries.

Think of a river. In some places, it’s wide and the water flows gently. In other places, the river narrows, and the water rushes through quickly. The Equation of Continuity explains this behavior – the water speeds up where the river is narrow because the area decreases, so the velocity must increase to maintain the balance.

Derivation:

The Equation of Continuity is based on the principle of conservation of mass, which states that mass cannot be created or destroyed within a closed system.

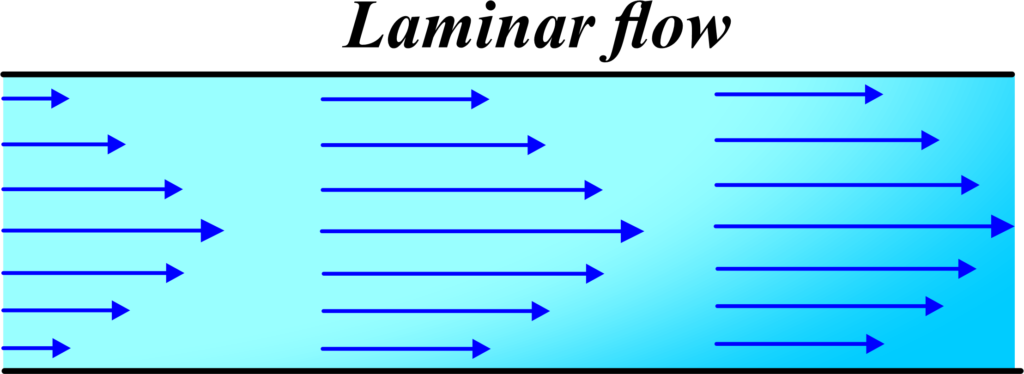
Imagine a pipe with varying cross-sectional areas through which an incompressible fluid (like water) is flowing. Let’s take two different sections of the pipe, section 1 with area (A₁) and section 2 with area (A₂).

In a small time interval (∆ t), the fluid will move a distance (∆ x₁) at section 1 with velocity (v₁) and (∆ x₂) at section 2 with velocity (v₂).

The volume of fluid passing through section 1 in time (∆ t) is (A₁ ∆ x₁), and through section 2 is (A₂∆ x₂).

The distance of each section of fluid travels is related to its velocity and time:

\(\displaystyle \Delta x_1 = v_1 \Delta t \)
\(\displaystyle \Delta x_2 = v_2 \Delta t \)

Since the fluid is incompressible, its density (ρ) remains constant. The mass of fluid passing through each section is the product of density and volume:

\(\displaystyle m_1 = \rho A_1 \Delta x_1 \)
\(\displaystyle m_2 = \rho A_2 \Delta x_2 \)

The mass entering section 1 must equal the mass leaving section 2 in the time (∆ t):

\(\displaystyle m_1 = m_2 \)
\(\displaystyle \rho A_1 \Delta x_1 = \rho A_2 \Delta x_2 \)

Replace (∆x₁ ) and (∆ x₂) with their respective expressions involving velocity and time:

\(\displaystyle \rho A_1 v_1 \Delta t = \rho A_2 v_2 \Delta t \)

The density (ρ) and time (∆ t) are the same on both sides of the equation, so they cancel out:

\(\displaystyle A_1 v_1 = A_2 v_2 \)

This gives us the Equation of Continuity for an incompressible fluid:

\(\displaystyle\begin{equation}\label{eqn:2}\boxed{\boldsymbol{A_1 v_1 = A_2 v_2 = \text{constant} }} \end{equation}\)

This equation tells us that the product of the cross-sectional area and the velocity at any two points along the pipe (or any conduit) is constant for an incompressible fluid. It implies that where the pipe narrows (small (A), the velocity (v) increases, and where the pipe widens (large A), the velocity (v) decreases.

Properties of Streamline Flow

Streamline flow, also known as laminar flow, is like a disciplined march of fluid particles, where each particle follows a specific path without wandering off. Here are the key properties:

• Parallel Layers: The fluid flows in parallel layers, with each layer sliding smoothly over the one below it, much like a stack of paper sliding over a desk.
• No Mixing: There’s no mixing or crossing between these layers. It’s as if each layer has its lane on a highway, and they all stick to their lanes.
• Constant Velocity: At any given point in the flow, the velocity of the fluid particles remains constant over time. If you were to watch a particle at a point, it would pass by at the same speed as the one before it.
• Orderly Paths: The motion of the fluid particles is orderly, with each following a path that’s predictable and steady. They move in straight lines or gentle curves that are parallel to the boundaries of the pipe or channel.
• Equation of Continuity: Streamline flow follows the equation of continuity, which means the product of the cross-sectional area (A) and the velocity (v) at any point is constant. So, \(\displaystyle A_1 v_1 = A_2 v_2 \), where 1 and 2 are two different points along the flow.
• Smooth Texture: When you look at a fluid in streamlined flow, it has a smooth texture. There are no ripples or eddies, and if you were to introduce a dye into the flow, it would form a thin line that follows the streamlines without dispersing.
• Low Reynolds Number: Streamline flow occurs at low Reynolds numbers, typically less than 2000, which indicates a smooth flow without turbulence.

What is Turbulent Flow?

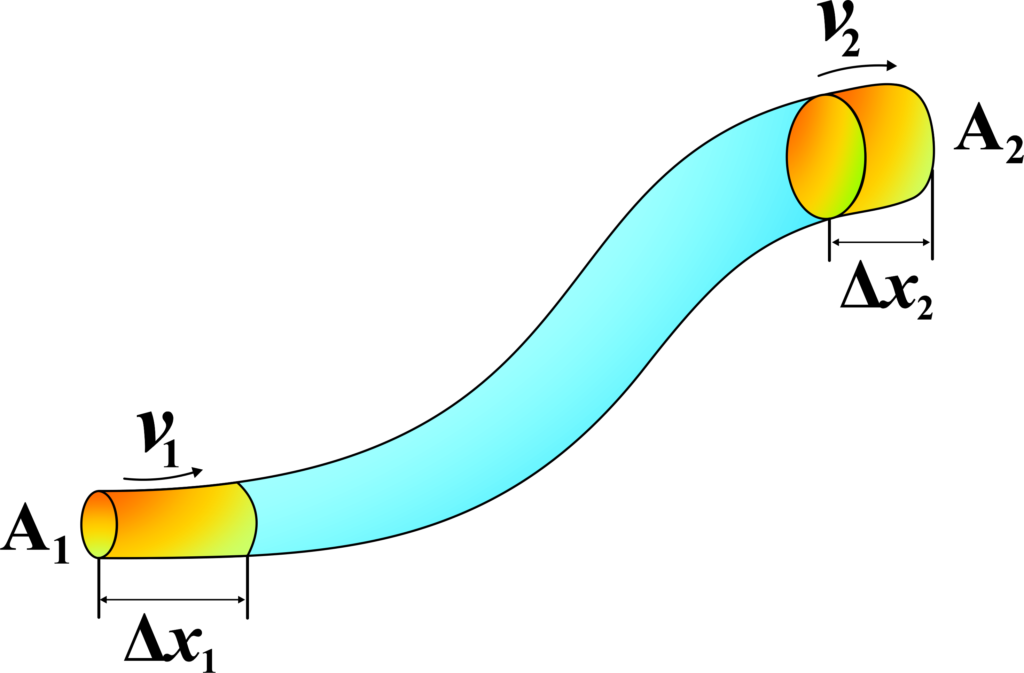
Turbulent flow is characterized by chaotic changes in pressure and flow velocity. It is the opposite of streamlined flow and occurs at high velocities or with large obstacles.

Turbulent flow is a type of fluid motion that is chaotic and unpredictable. Unlike streamlined flow, where the fluid moves in orderly layers, turbulent flow is characterized by irregular fluctuations and mixing. It’s like the difference between a crowd walking in an organized line and a bustling market where everyone is moving in different directions.

Here’s what makes turbulent flow stand out:

• Irregular Fluctuations: The speed and direction of the fluid at any point change continuously and randomly.
• Mixing: Fluid particles mix as they move, creating swirls and eddies.
• Eddies: These are small whirlpools or vortices within the fluid, which are a hallmark of turbulence.
• Energy Dissipation: Turbulent flow tends to dissipate energy through these eddies, which is why it requires more energy to maintain than laminar flow.
• Common in Nature: Many natural flows are turbulent, like the flow of rivers, wind, and blood through arteries.

Turbulent Flow Equation

There isn’t a single equation for turbulent flow due to its complexity, but the Navier-Stokes equations govern the motion of fluid particles in turbulent flow.

When we talk about turbulent flow, we’re dealing with a fluid motion that is chaotic and full of vortices, unlike the orderly layers of streamline flow. Now, there isn’t a single equation that can describe the entire state of a turbulent flow because of its complexity. However, we can use the Reynolds number to predict whether a flow will be laminar or turbulent.

The Reynolds number (Re) is a dimensionless value that helps determine the flow regime of a fluid. It’s given by the equation:

\(\displaystyle\begin{equation}\label{eqn:3}\boxed{\boldsymbol{ Re = \frac{\rho v D}{\eta} }} \end{equation}\)

• (ρ) is the fluid density in (kg/m³).
• (v) is the flow velocity in (m/s).
• (D) is the characteristic linear dimension (like the diameter of a pipe) in (m).
• (η) is the dynamic viscosity in (Pa.s).

A low Reynolds number indicates laminar flow, where viscous forces are dominant, and the flow is smooth and orderly. A high Reynolds number suggests turbulent flow, where inertial forces are dominant, leading to chaos and mixing within the fluid.

For a flow to transition from laminar to turbulent, the Reynolds number typically needs to exceed a critical value, which is around 2300 for flow in a circular pipe. Beyond this value, the flow becomes increasingly chaotic and turbulent.

Characteristics of a Turbulent Flow

Imagine you’re standing by a river, and you see water flowing smoothly in one area, but in another, it’s swirling and churning. That churning part is what we call turbulent flow. Here’s what makes it unique:

• Irregularity: Turbulent flow is unpredictable. Unlike the smooth and steady flow of water from a tap, turbulent flow is more rapid, where water moves erratically in all directions.
• Vortices and Eddies: In turbulent flow, you’ll find mini whirlpools or swirls, known as vortices and eddies. These are small pockets of rotational movement within the fluid.
• Mixing: Turbulent flow is great at mixing things up. If you pour some colored dye into a turbulent stream, you’ll see it quickly mix throughout the water, unlike in a smooth stream where it would stay in a neat line.
• Diffusion: Because of all the mixing, substances in turbulent flow spread out, or diffuse, much faster than in laminar flow.
• Energy Loss: Turbulent flow is a bit of an energy hog. It takes more energy to maintain because of all the chaotic movement and friction between the fluid layers.

To sum it up, turbulent flow is like a chaotic dance of fluid particles, moving in all directions, mixing things up, and using more energy. It’s the opposite of the orderly, layer-by-layer movement you see in laminar flow.

Different Correction Factors

When we study fluid flow, we often start with ideal conditions where the fluid is perfect, and everything flows smoothly. But in reality, fluids have properties like viscosity (stickiness) and can be compressed, which affects how they flow. That’s where correction factors come in. They help us adjust our calculations to match what actually happens in the real world.

Here are some key correction factors:

• Momentum Correction Factor: This factor, often denoted as (\beta), adjusts the momentum calculations to account for the fact that fluid velocity isn’t the same everywhere in a pipe. Fluid moves faster in the center than near the edges because of friction.
• Energy Correction Factor: Similar to the momentum correction factor, this adjusts the energy calculations because the energy distribution isn’t uniform across the pipe’s cross-section.
• Coefficient of Discharge: When fluid flows through an opening or a valve, not all of it gets through perfectly. This factor corrects for the amount of fluid that actually flows compared to the ideal flow.
• Friction Factor: Pipes aren’t perfectly smooth, and this roughness slows down the fluid. The friction factor accounts for the energy loss due to the pipe’s roughness.
• Expansion and Contraction Coefficients: When a pipe suddenly gets wider or narrower, the flow changes speed. These coefficients correct for the changes in pressure and velocity when the pipe’s diameter changes.

Correction factors are like the adjustments you make to a recipe when you’re cooking at high altitude. You know the basic recipe (the ideal fluid flow equations), but you need to tweak it a bit (apply correction factors) to get the best results (accurate predictions of real fluid flow). They’re essential tools for engineers and physicists to make sure that their designs work properly in the real world, not just on paper.

What is Reynolds Number?

The Reynolds number is a dimensionless quantity used to predict the flow regime in a fluid. Imagine you’re trying to slide down a water slide. If the water is flowing smoothly and you’re sliding down without any bumps, that’s like laminar flow. But if the water is gushing down and you’re getting jostled around, that’s like turbulent flow. The Reynolds number is like a score that tells us whether the flow is going to be smooth (laminar) or rough (turbulent).

• Reynolds Number (Re): It’s a number without any units (like how a score doesn’t have units like meters or seconds) that compares two forces in the fluid—inertial forces (which want to keep the fluid moving) and viscous forces (which want to slow it down).

The formula for the Reynolds number is

\(\displaystyle\begin{equation}\label{eqn:4}\boxed{\boldsymbol{ Re = \frac{\rho v L}{\mu}}} \end{equation}\)

– (ρ) is the fluid’s density (how much stuff is packed into it),
– (v) is the velocity (speed) of the fluid,
– (L) is a characteristic length (like the diameter of a pipe),
– (µ) is the dynamic viscosity (how sticky or thick the fluid is).

The Reynolds number helps us understand the type of flow we’ll see in a fluid. It’s a dimensionless number, meaning it doesn’t have any units like meters or seconds. It’s all about comparing two types of forces in the fluid: inertial forces (which are related to the mass of the fluid and want to keep the fluid moving) and viscous forces (which are related to the fluid’s stickiness and want to slow it down).

These forces depend on the mass of the fluid moving and its velocity. The mass of the fluid can be represented by its density (ρ), and when we multiply this by the velocity (v) and a characteristic length (L) like the diameter of a pipe, we get a measure of the inertial forces.

These forces depend on the fluid’s viscosity (µ) and the velocity gradient across the fluid. For our purposes, we’ll just consider the viscosity and the characteristic length.

To find the Reynolds number, we compare the inertial forces to the viscous forces. We do this by dividing the measure of inertial forces by the measure of viscous forces.

Putting it all together, we get the formula for the Reynolds number:

\(\displaystyle Re = \frac{\text{Inertial Forces}}{\text{Viscous Forces}} = \frac{\rho v L}{\mu} \)

• (Re) is the Reynolds number,
• (ρ) is the density of the fluid,
• (v) is the velocity of the fluid,
• (L) is a characteristic length (like the diameter of a pipe),
• (µ) is the dynamic viscosity of the fluid.

So, the Reynolds number is essentially a ratio of the tendency of the fluid to keep moving (inertia) versus its tendency to resist flow (viscosity). A higher Reynolds number indicates a higher likelihood of turbulent flow, while a lower number indicates laminar flow. A low Reynolds number (less than about 2000) means the flow is likely to be laminar—smooth and orderly. A high Reynolds number (more than about 4000) means the flow is likely to be turbulent—chaotic and mixed up. It’s like a battle between the fluid wanting to move freely and its stickiness trying to hold it back.

Also Read: Viscosity

Transition From Laminar Flow to Turbulent Flow

The transition occurs when the Reynolds number exceeds a critical value, typically around 2300 for flow in a circular pipe. The transition from laminar to turbulent flow is like going from a peaceful river to a wild rapid.

Imagine you’re at a water park sliding down a smooth, straight water slide. At first, the water around you is flowing nicely and smoothly, which is what we call laminar flow. But as you go faster or the slide gets bumpy, the water starts to swirl and create little whirlpools. This is the beginning of turbulent flow.

Here’s what happens during the transition:

• Laminar Flow: In laminar flow, the fluid moves in straight, orderly layers. It’s calm and predictable, like a gentle stream.
• Increasing Speed or Obstacles: As the fluid’s speed increases or it encounters obstacles (like bumps in our water slide), the flow starts to change.
• Instability: Small disturbances in the flow, which are normally smoothed out by the fluid’s viscosity, start to grow instead of dying down.
• Turbulent Flow: Eventually, these disturbances become so large that they dominate the flow, turning it into turbulent flow, which is chaotic and full of eddies and vortices.

The point at which this transition happens can be predicted by the Reynolds number. For most flows, when the Reynolds number exceeds about 2000, the flow tends to become turbulent. However, this transition doesn’t happen suddenly; it’s a gradual process where the flow can be a mix of laminar and turbulent, known as transitional flow.

Difference between Laminar and Turbulent Flow

A table that highlights the key differences between laminar flow and turbulent flow.

Aspect	Laminar Flow	Turbulent Flow
Flow Pattern	Smooth and orderly, with fluid moving in parallel layers.	Chaotic and irregular, with eddies and vortices.
Velocity	Velocity of the fluid is consistent and predictable.	Velocity varies significantly and unpredictably.
Layers	Fluid layers slide past each other smoothly with little to no mixing.	Fluid layers mix intensely due to the irregular movement.
Noise and Vibration	Generally quiet with minimal vibration.	Often noisy with significant vibration.
Energy Consumption	Lower energy loss due to less friction between layers.	Higher energy loss due to more friction and mixing.
Reynolds Number	Typically less than 2000.	Typically greater than 4000.
Applications	Suitable for processes requiring stable and predictable flow, like in inkjet printers.	Common in natural and industrial processes, like in rivers or HVAC systems.

Solved Examples

Example 1: Calculate the Reynolds number for water flow through a pipe with a diameter of (0.1 m), a flow velocity of (2 m/s), and a dynamic viscosity of \(\displaystyle 1 \times 10^{-3} \, \text{Pa} \cdot \text{s}\).

Solution: The Reynolds number (Re) can be calculated using the formula:

\(\displaystyle Re = \frac{\text{Density} \times \text{Velocity} \times \text{Diameter}}{\text{Dynamic viscosity}} \)

Given:

• Density of water (ρ) = (1000 kg/m³)
• Velocity (v) = (2 m/s)
• Diameter (D) = (0.1 m)
• Dynamic viscosity (η) = \(\displaystyle1 \times 10^{-3} \, \text{Pa} \cdot \text{s}\)

Substituting the given values:

\(\displaystyle Re = \frac{1000 \times 2 \times 0.1}{1 \times 10^{-3}} \)
\(\displaystyle Re = \frac{200}{1 \times 10^{-3}} \)]
\(\displaystyle Re = 2 \times 10^5 \)

So, the Reynolds number for the given flow is \(\displaystyle 2 \times 10^5\), indicating turbulent flow.

Example 2: Calculate the drag coefficient for an object experiencing laminar flow with a Reynolds number of (5000).

Solution: For laminar flow, the drag coefficient (C_d) can be calculated using empirical formulas or experimental data. For (Re < 2000), the Hagen-Poiseuille equation can be used:

\(\displaystyle C_d = \frac{24}{Re} \)

Given (Re = 5000), which falls in the laminar flow regime, we can use the above formula:

\(\displaystyle C_d = \frac{24}{5000} \)
\(\displaystyle C_d \approx 0.0048 \)

So, the drag coefficient for the laminar flow with (Re = 5000) is approximately (0.0048).

Example 3: A fluid with a density of (900 kg/m³) flows through a pipe that narrows from a radius of 0.3 m to 0.15 m. If the velocity of the fluid in the wider section is 1.5 m/s, what is the velocity in the narrower section?

Solution: Using the equation of continuity:

\(\displaystyle A_1v_1 = A_2v_2 \)

The cross-sectional areas are:

\(\displaystyle A_1 = \pi r_1^2 = \pi (0.3)^2 \)
\(\displaystyle A_2 = \pi r_2^2 = \pi (0.15)^2 \)

Now, we can find (v₂):

\(\displaystyle v_2 = \frac{A_1}{A_2} v_1 \)
\(\displaystyle v_2 = \frac{\pi (0.3)^2}{\pi (0.15)^2} \times 1.5 \)
\(\displaystyle v_2 = 4 \times 1.5 \)
\(\displaystyle v_2 = 6 \text{ m/s} \)

FAQs