The study of stress and strain dates back to the early days of engineering and physics, where understanding the behavior of materials under different forces was crucial for building structures.
The journey begins with the Renaissance genius Leonardo da Vinci, who sketched ideas for testing the strength of wires. Then came Galileo Galilei, who, in the early 17th century, investigated the breaking loads of rods and beams, laying the groundwork for understanding stress.
The English scientist Robert Hooke in 1660 discovered a principle that would become the cornerstone of elasticity and material science: Hooke’s Law. He found that, up to a certain point, the way a material deforms is proportional to the force applied to it.
The Bernoulli family, particularly Jakob Bernoulli, and the brilliant Leonhard Euler in the late 17th and early 18th centuries, made significant contributions. They began to describe deformation in terms of force per unit area (stress) and elongation per unit length (strain), which are the definitions we use today.
The term ‘elasticity’ was developed further by scientists like Edme Mariotte in France and Thomas Young in Britain in the 18th and 19th centuries. They explored how materials return to their original shape after being deformed, which is a property we now call ‘elasticity’.
The modern theory of stress and strain was significantly advanced in the 1940s and 1950s by Ronald S. Rivlin, who developed stress-strain relations for rubbery elastic materials and helped us understand the physical effects of nonlinearity in materials.
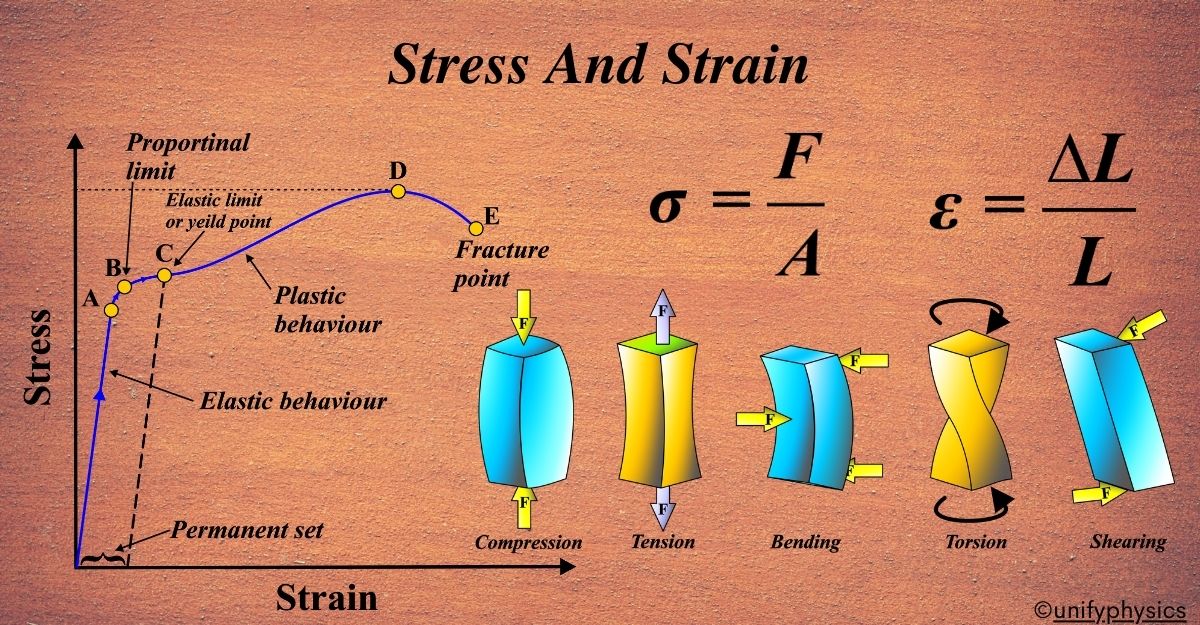
What is Stress?
Stress is defined as the force applied per unit area of a material. It’s like the pressure you feel when you push against a wall.
Imagine you’re trying to push a heavy box across the floor. The force you’re applying on the box over the area of contact is what we call Stress in physics. It’s a measure of how much force is acting on a certain area of a material.
In more scientific terms, stress is the internal force that particles of a material exert on each other when an external force is applied. It’s calculated by dividing the force (F) by the area (A) over which the force is distributed. Here’s the formula:
\(\displaystyle \sigma = \frac{F}{A} \)
where (σ) is the stress, (F) is the force you apply, and (A) is the area over which the force acts.
The unit of stress is the Pascal (Pa), which is equivalent to one Newton per square meter (N/m²). So, when you’re pushing that box, if you apply a force of one Newton over an area of one square meter, you’re exerting the stress of one Pascal.
Think of a bridge with cars driving over it. The weight of the cars applies a force to the bridge. The part of the bridge where the tires touch is the area over which the force is spread. The bridge experiences stress at those points, and engineers need to calculate this to make sure the bridge can handle the load.
Understanding stress is crucial because it helps us predict how materials will behave under different forces. Will the material stretch, compress, or maintain its shape?
So, stress is all about how much ‘push’ or ‘pull’ is happening in a material and how that might change its shape or volume. It’s a fundamental concept that helps us design and build the world around us.
Types of Stress
Stress, in the world of physics, is like the different ways you can pull or push on a spring. It’s all about how forces act on objects and what kind of ‘squeeze’ or ‘stretch’ they cause. Stress is generally divided into two main types based on how the force is applied to an object:
Normal Stress
This happens when the force is perpendicular to the surface. Imagine pressing your thumb straight down onto a sponge; that’s normal stress.
Tensile Stress
It’s a ‘pulling’ stress. When you stretch a rubber band, you’re applying tensile stress. When forces pull on an object and try to stretch it. Imagine you have a rubber band between your fingers. When you pull on both ends, you’re applying a force that stretches the rubber band. This stretching force is what we call Tensile Stress in physics.
Tensile Stress is a type of normal stress that occurs when a material is subjected to a force that tries to stretch it. It’s the ‘pulling’ stress acting perpendicular to the cross-sectional area of the material.
\(\displaystyle \sigma = \frac{F}{A} \)
where (σ) is the tensile stress, (F) is the pulling force applied, and (A) is the cross-sectional area over which the force acts.
Materials respond differently to tensile stress:
- Ductile materials can stretch more and handle tensile stress better.
- Brittle materials are more likely to break under tensile stress.
Elastic Modulus or Young’s Modulus is a measure of a material’s stiffness and is used to calculate how much it will stretch under tensile stress. The Ultimate Tensile Stress (UTS) is the maximum stress a material can withstand before it breaks.
Think of a steel cable holding up a heavy elevator. The weight of the elevator applies a pulling force on the cable, causing tensile stress. Engineers need to calculate this stress to ensure the cable can support the elevator without breaking. So, tensile stress is all about the ‘stretch’ in a material when it’s pulled.
Compressive Stress
It’s a ‘pushing’ stress. When you press both ends of a spring together, you’re applying compressive stress. Compressive Stress is when a material experiences a ‘pushing’ force that tries to reduce its size or volume. Imagine you’re holding a sponge between your hands. When you press your hands together, you’re squishing the sponge. This ‘squishing’ force is what we call Compressive Stress in physics.
Compressive Stress is a type of normal stress that occurs when a material is subjected to a force that tries to squash or compress it. It’s the ‘pushing’ stress acting perpendicular to the cross-sectional area of the material. Materials under compressive stress can either deform slightly and return to their original shape or permanently change shape, depending on the amount of stress and the material’s properties. The unit of compressive stress is also the Pascal (Pa), just like tensile stress.
Think of a column in a building that supports floors above. The weight of the floors applies a compressing force on the column, causing compressive stress. Engineers calculate this stress to ensure the column can support the weight without collapsing. Different materials have varying capacities to handle compressive stress. For example, concrete is strong under compression but weak under tension. So, compressive stress is all about the ‘squeeze’ in a material when it’s pushed.
Shear Stress
This occurs when the force is parallel to the surface. It’s like when you use scissors to cut paper; the blades apply shear stress. Shear Stress is a type of stress that occurs when forces act parallel to the surface of a material, causing layers to slide over each other. It’s like the force you use to shuffle a deck of cards; each card slides over the one below it.
Imagine you have a deck of cards. If you apply a force to the top card and slide it parallel to the card below, you’re creating what’s known as Shear Stress.
Shear Stress occurs when forces are applied parallel to the surface of a material, causing the layers to slide over each other. It’s like the force you use to cut with scissors: one blade pushes one way, the other blade pushes the opposite way, and the paper in between gets cut.
To visualize shear stress, think about:
- Spread butter on toast with a knife.
- The force you apply when you’re trying to shift a heavy book across a table.
Shear stress isn’t just a physics term; it’s part of everyday life. When you walk, the friction between your shoes and the ground creates shear stress. Even the earth experiences shear stress during an earthquake, as tectonic plates slide past each other. So, shear stress is all about the sliding and gliding of layers in materials when forces act parallel to those layers.
Various Types Of Stress
Let’s break down the various types of stress encountered in physics, including tension, compression, shear, bending, and torsion.
Tension: Imagine you’re pulling on a rope from both ends. Tension stress occurs when a material experiences a stretching force, pulling its molecules apart. Think of it like stretching a rubber band – the force pulls the material in opposite directions, causing it to elongate. This type of stress is common in structures like bridges, where the weight of the roadway pulls down on the cables.
Compression: Now, imagine you’re squashing a sponge. Compression stress occurs when a material experiences a pushing force that tries to reduce its size or volume. It’s like squeezing a soft object between your hands. Compression stress can cause materials to compact or buckle under the applied force. Think of how the columns in a building support the weight of the floors above, experiencing compression stress as they bear the load.
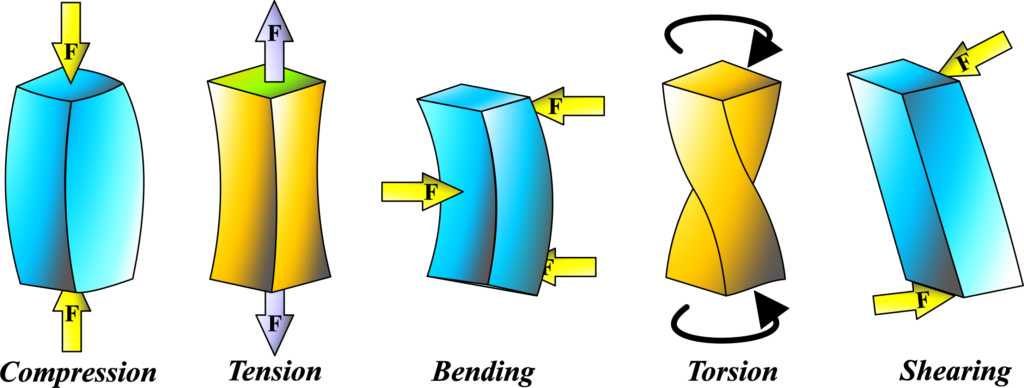
Shear: Picture sliding one hand against the other in opposite directions. Shear stress occurs when forces act parallel to each other but in opposite directions, causing layers of material to slide past each other. It’s like cutting through a piece of paper with scissors. Shear stress can cause materials to deform or fail along a plane. For example, think of how earthquakes generate shear stress along fault lines, causing rocks to slip past each other.
Bending: Imagine pushing down on one end of a ruler placed across a table. Bending stress occurs when a material is subjected to forces that bend it, causing one part to compress and the other to stretch. It’s like when you bend a stick or a beam. Bending stress is common in structures like bridges and beams, where the weight or load causes them to bend downward.
Torsion: Picture twisting a towel to wring out water. Torsion stress occurs when a material is twisted by a torque or twisting force applied at one end while the other end remains fixed. It’s like when you twist a screwdriver or a wrench. Torsion stress can cause materials to twist or deform along their length. For example, think of how a shaft in a car’s engine experiences torsion stress as it transmits power from the engine to the wheels.
These types of stress are essential in physics and engineering because they help us analyze and design structures and materials that can withstand various forces and loads. Whether it’s building bridges, designing machinery, or studying natural phenomena like earthquakes, knowing how different types of stress affect materials is crucial for solving real-world problems.
What is Strain?
Strain is the measure of deformation or change in shape due to applied stress. It’s a dimensionless quantity representing the relative change in shape. Think of a spring or a rubber band. When you pull on it, it stretches, right? Strain is a measure of how much something stretches or compresses when a force is applied to it.
In physics, strain is the change in shape or size of an object due to an applied force, compared to its original shape or size. It’s a way to describe how much an object is ‘strained’ by the force.
Strain is a ratio and doesn’t have any units—it’s a dimensionless quantity. It’s calculated by dividing the change in length, volume, or shape by the original length, volume, or shape. In other words, the amount of strain can be expressed as a change in length, volume, or shape relative to the original dimensions. For example, if you stretch a rubber band to twice its original length, the strain would be 1, or 100%. Strain can be caused by forces that pull (tensile), push (compressive), or slide (shear) an object.
Types of Strain:
There are different types of strain based on how the force is applied: When you pull on something and it stretches, like a rubber band or a spring, that’s tensile strain in action. It’s a measure of how much something has been stretched.
Tensile Strain
Tensile Strain is the change in length of an object under tensile stress (the pulling force) compared to its original length. It’s a way to describe how much an object has been elongated due to the applied force. Tensile strain is a dimensionless quantity, meaning it has no units.
To visualize tensile strain, think about:
- A balloon inflates as you fill it with air.
- A bridge expands on a hot day due to the heat.
Tensile Strain shows the deformation of materials under tensile stress, like stretching a rubber band. Materials with high tensile strain can stretch more without breaking.
So, tensile strain is all about how much ‘stretch’ an object undergoes when it’s pulled.
Compressive Strain
Compressive Strain is the deformation that occurs when an object is subjected to forces that push it together, causing it to shorten or decrease in volume. When you press on something and it gets shorter or smaller, like compressing a sponge, that’s compressive strain. It’s a measure of how much something has been squished.
Compressive Strain is the change in length of an object under compressive stress (the pushing force) compared to its original length. It’s a way to describe how much an object has been shortened due to the applied force. To visualize compressive strain, think about:
- A spring that gets shorter when you press it.
- A box that gets squished when something heavy is placed on it.
It’s a dimensionless quantity, meaning it doesn’t have units; it’s simply a ratio of the change in length to the original length. Understanding compressive strain is essential for materials that need to withstand squeezing forces, such as columns in buildings or the materials used in protective gear. So, compressive strain is all about how much ‘squeeze’ an object undergoes when it’s pushed.
Shear Strain
Shear Strain is the measure of how much the shape of an object changes due to shear stress. It represents the change in angle between two lines or planes within a material that were originally at right angles. Shear strain is denoted by the Greek letter gamma (γ) and is a dimensionless quantity, often measured in radians
Imagine you have a stack of papers. When you apply force to the top sheet and slide it sideways, the sheets no longer line up perfectly at the corners. This change in angle at the corners is what we call a Shear Strain.
Shear Strain is the measure of how much the shape of an object has changed due to shear stress. It’s not about stretching or compressing; it’s about the change in angle between different parts of the object. The shear strain does not involve a volume change; it’s purely a change in shape. To visualize shear strain, think about:
- The way layers of soil move relative to each other during a landslide.
- The distortion of the shape of a book when you apply force to its cover, sliding it against the pages.
So, shear strain is all about the change in angle due to sliding forces.
Stress-Strain Curve
A Stress-Strain Curve is a graph that shows the relationship between stress and strain for a material. It helps us understand how a material will behave when subjected to forces.
Imagine you’re testing a piece of material, like a rubber band or a metal wire, by stretching or compressing it. As you apply force to the material, you’re subjecting it to stress. Stress is like the pressure or force you’re exerting on the material.
Now, as you keep applying force, the material starts to deform. Deformation means it changes shape or size in response to the stress. This deformation is measured by something called strain. Strain is like how much the material stretches or compresses under the applied stress.
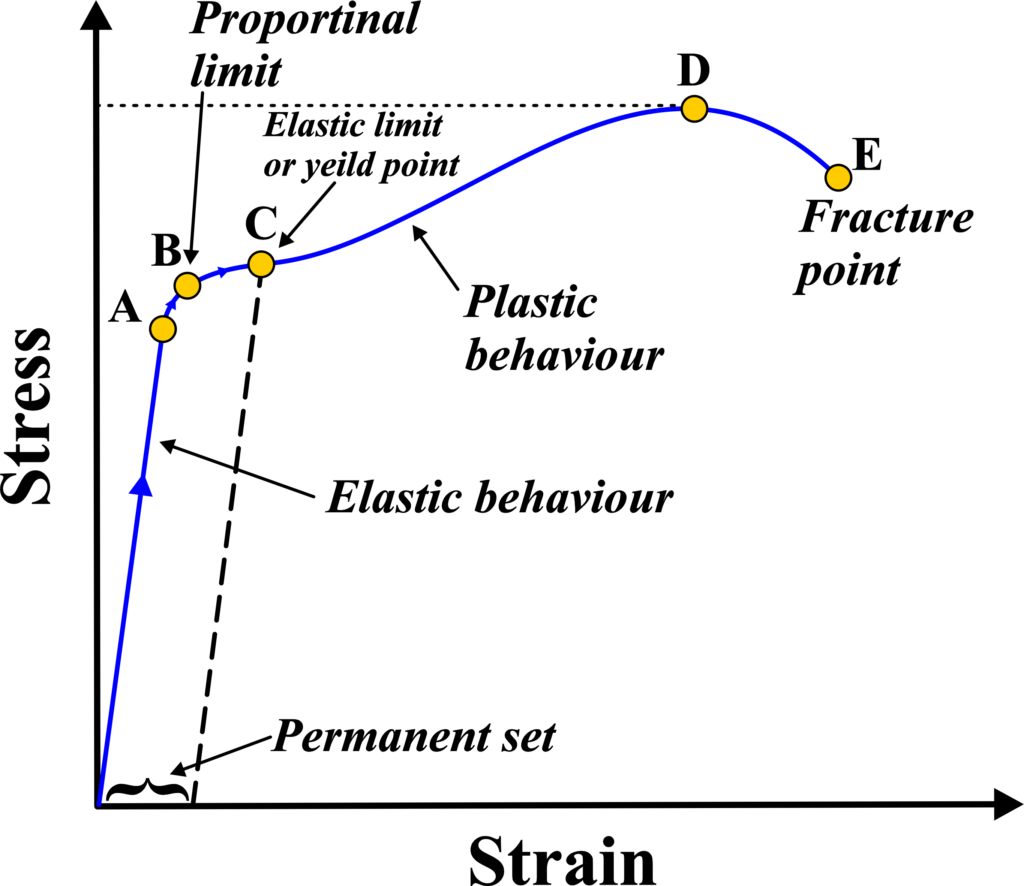
The stress-strain curve simply shows us how the material responds to different levels of stress. On the graph, stress is usually plotted on the y-axis (stress) and strain on the x-axis (strain).
At the beginning of the curve, when you apply a small amount of stress, the material behaves elastically. This means it deforms temporarily but returns to its original shape once you remove the force.
Think of stretching a rubber band and then letting go – it snaps back to its original size. As you increase the stress, you reach a point called the yield point. Beyond this point, the material starts to deform plastically. Plastic deformation means the material changes shape permanently, even after you remove the force. Picture bending a paperclip – once you bend it past a certain point, it stays bent.
Finally, if you keep increasing the stress, you’ll reach a breaking point called the ultimate tensile strength. This is the maximum stress the material can handle before it breaks.
The stress-strain curve typically consists of several distinct regions:
Proportional Limit: This is the initial straight part of the curve where stress and strain are directly proportional to each other. If you apply a force to a material, it will stretch, and the amount it stretches is directly related to the force. This is where Hooke’s Law applies, which says that the force needed to extend or compress a spring by some distance is proportional to that distance.
Elastic Region: In this region, the material will return to its original shape when the force is removed. It’s like a rubber band that you stretch and then let go—it snaps back to its original length. This region ends at the yield point.
Yield Point: The yield point is where the material starts to deform permanently. If you bend a paperclip back and forth, it eventually stays bent—that’s because it has passed its yield point. The material won’t return to its original shape entirely if the force is removed.
Ultimate Stress Point: This is the peak point on the curve and represents the maximum stress that the material can withstand while being stretched. Beyond this point, the material will start to neck and eventually break. It’s like stretching a piece of chewing gum until it snaps.
Fracture or Breaking Point: Finally, the fracture point is where the material breaks or fractures. If you’ve ever snapped a stick in half, you’ve taken the material past its ultimate stress point to its breaking point. This is the end of the stress-strain curve.
Strength Of Material
Ductile Materials
Ductile materials, such as mild steel, aluminum, and gold, offer the advantage of significant plastic deformation before breaking. Their ability to stretch into wires or bend into shapes without fracturing makes them ideal for structures subjected to stretching and bending forces.
- Ductile materials show a significant area under the curve in the plastic region, indicating they can undergo a lot of plastic deformation before breaking.
- The graph starts with a linear elastic region where Hooke’s Law applies.
- After the yield point, the material stretches significantly, showing a large plastic region before reaching the ultimate tensile strength and eventually breaking.
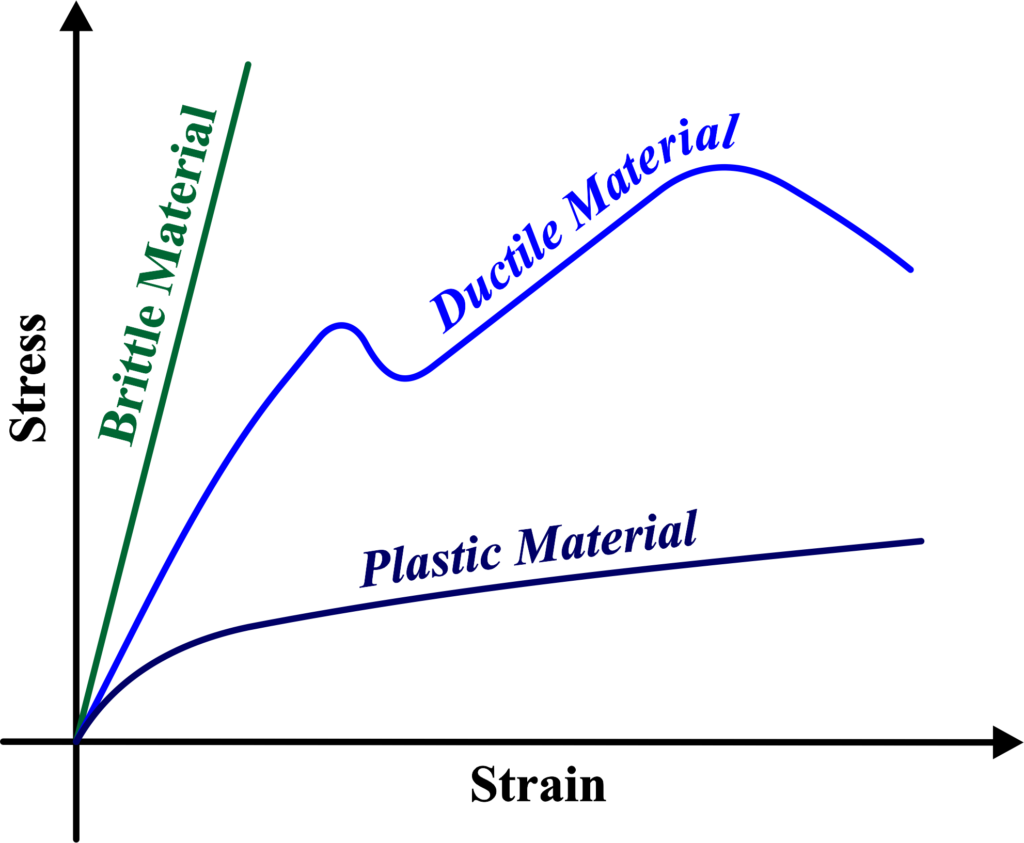
Brittle Materials
On the contrary, brittle materials like glass and ceramics lack this flexibility. They break with little to no plastic deformation, often fracturing abruptly under applied forces, posing challenges in applications where sudden failure is not acceptable.
- Brittle materials have a stress-strain curve with a very steep initial elastic region and very little to no plastic region.
- They break with little elastic and insignificant plastic deformation.
- The graph for brittle materials shows that they can handle stress up to a high point but will break suddenly without much warning.
Plastic Materials
Plastic materials, including many metals, exhibit a unique behavior under stress. They can deform permanently without breaking, thanks to their yield point where plastic deformation begins. Once deformed, these materials do not return to their original shape after the force is removed.
- Plastic materials can deform permanently under stress without breaking.
- Their stress-strain graph will show a yield point followed by a significant plastic region, indicating the material can be molded or permanently deformed¹.
These graphs are crucial in materials science as they help predict how a material will behave under stress, which is essential for designing safe and functional products and structures.
This property is advantageous in manufacturing processes where shaping and molding are required. Engineers must carefully consider these material properties when selecting materials for engineering applications, ensuring structural integrity, safety, and optimal performance in various scenarios. By understanding the characteristics of ductile, brittle, and plastic materials, engineers can make informed decisions that contribute to the success and reliability of their projects.
Also Read: Elastic Behavior Of Solids
Difference Between Stress And Strain
The main difference is that stress is the cause (force applied) and strain is the effect (deformation).
| Stress | Strain |
|---|---|
| It’s the force applied per unit area. | It’s the measure of deformation due to the applied force. |
| Stress has units, typically Pascals (Pa). | Strain is a dimensionless quantity; it has no units. |
| Stress can be tensile, compressive, or shear. | Strain can be tensile, compressive, or shear, corresponding to the type of stress. |
| It’s calculated using the formula: \(\displaystyle \sigma = \frac{F}{A} \) | It’s calculated as the change in dimension over the original dimension, for example, length: \(\displaystyle \epsilon = \frac{\Delta L}{L_0} \) |
| Stress describes the cause of deformation. | Strain describes the effect or result of stress. |
This table should help students differentiate between stress and strain, understanding that stress is about the ’cause’ (the force applied) and strain is about the ‘effect’ (how the material responds).
Hooke’s Law
Hooke’s Law states that the strain in a solid is directly proportional to the applied stress within the elastic limit of that solid.
Hooke’s Law is like a friend that tells us how springs behave when we stretch or squash them. Imagine you have a spring in your hand. Now, when you stretch the spring by pulling it, what happens? It gets longer, right? Hooke’s Law tells us that the force needed to stretch or squash a spring is directly proportional to how much you stretch or squash it.
In other words, the more you stretch the spring, the harder you have to pull. But here’s the cool part: Hooke’s Law also tells us that if you stretch the spring and then let go, it will bounce back to its original shape. It’s like the spring saying, “Hey, thanks for pulling me, but I’m going back to where I belong now!”
Hooke’s Law states that the force needed to extend or compress a spring by some distance is proportional to that distance, as long as the limit of elasticity (the material’s ability to return to its original shape) is not exceeded. The law is usually expressed by the equation:
\(\displaystyle F = kx \)
- (F) is the force applied to the spring,
- (k) is the spring constant (a measure of the stiffness of the spring),
- (x) is the extension or compression of the spring from its original length.
This principle doesn’t just apply to springs. It applies to any elastic material, like rubber bands or even the muscles in your body. Engineers use Hooke’s Law to design objects that need to return to their original shape after being deformed, like car suspensions and sports equipment.
Hooke’s Law only holds up to the elastic limit of the material. If you stretch a spring too much, it won’t return to its original shape—that’s when Hooke’s Law breaks down, and the material is said to be deformed plastically. In other words, Hooke’s Law is valid only up to the proportional limit; beyond this point, the material will not return to its original shape.
Hooke’s Law Applications
Hooke’s Law is used in designing springs and calculating the load they can handle. Hooke’s Law isn’t just a theory; it has practical uses in our daily lives and various scientific fields. Let’s look at some of the applications:
- Spring Scales: These devices measure weight by the stretch of a spring according to Hooke’s Law. The more the spring stretches, the heavier the object.
- Manometers: These instruments use springs to measure pressure. The change in pressure causes a spring to compress or extend, and Hooke’s Law helps calculate the pressure based on that movement.
- Mechanical Clocks: The balance wheel in a clock uses a spring. It oscillates back and forth, and Hooke’s Law ensures the clock keeps accurate time by regulating the wheel’s movement.
- Seismology: To measure earthquakes, seismographs use springs. When the ground shakes, the spring moves, and scientists use Hooke’s Law to interpret the data and understand the earthquake’s magnitude.
- Acoustics: In musical instruments like guitars, the strings vibrate according to Hooke’s Law, producing sound. The tension in the strings determines the pitch of the note.
- Suspension Systems: Cars and bikes have suspension systems with springs that absorb shocks. Hooke’s Law helps design these systems to ensure a smooth ride by predicting how the springs will react to bumps.
- Engineering and Construction: When designing buildings and bridges, engineers use Hooke’s Law to make sure the materials will handle stress without deforming permanently.
- Medical Devices: Some medical equipment, like stethoscopes and blood pressure cuffs, use springs that follow Hooke’s Law to function correctly.
- Sports Equipment: The springs in gym equipment and the elasticity in sports balls like basketballs and soccer balls are designed considering Hooke’s Law to ensure they perform as expected.
These applications show how Hooke’s Law helps us understand and predict the behavior of materials under force, making it a fundamental principle in science and engineering.
Hooke’s Law Disadvantages:
While Hooke’s Law is fundamental in understanding the behavior of elastic materials, it has its limitations:
- Limited to the Elastic Region: Hooke’s Law is only valid within the elastic limit of materials. If the material is stretched beyond this point, it won’t return to its original shape, and Hooke’s Law no longer applies.
- Small Forces and Deformations: The law provides accurate results only when the forces and deformations involved are small. For larger forces that cause significant deformations, the relationship between stress and strain may not be linear.
- Not Universal: Hooke’s Law isn’t a universal principle. It applies well to many materials but not all. Some materials deviate from the linear relationship even within their elastic limits.
- Solid Bodies Only: The law is most accurate for solid bodies. It doesn’t necessarily apply to other states of matter like liquids or gases where the behavior under stress can be very different.
Solved Examples
Example 1: A steel wire of length (2 m) and diameter (3 mm) is stretched by a force of (500 N). If Young’s modulus of steel is \(\displaystyle 2\times 10^{11} \, N/m^2\), calculate the stress and strain produced in the wire.
Solution: Given;
- Length of the wire, (L = 2 m)
- Diameter of the wire, (d = 3, mm = 0.003 m)
- Applied force, (F = 500, N)
- Young’s modulus of steel, \(\displaystyle Y = 2 \times 10^{11} \, N/m^2\)
First, we need to find the cross-sectional area of the wire:
\(\displaystyle A = \frac{\pi d^2}{4} \)
\(\displaystyle A = \frac{\pi \times (0.003)^2}{4} \)
\(\displaystyle A = \frac{\pi \times 0.000009}{4} \)
\(\displaystyle A = \frac{\pi}{4000000} \, m^2 \)
Now, we can calculate the stress (σ) using the formula:
\(\displaystyle \sigma = \frac{F}{A} \)
\(\displaystyle \sigma = \frac{500}{\frac{\pi}{4000000}} \)
\(\displaystyle \sigma = \frac{500 \times 4000000}{\pi} \, N/m^2 \)
\(\displaystyle \sigma \approx 159154.943 \, N/m^2 \)
Next, we calculate the strain (\(\displaystyle\epsilon\)) using Hooke’s law:
\(\displaystyle \epsilon = \frac{\sigma}{Y} \)
\(\displaystyle \epsilon = \frac{159154.943}{2 \times 10^{11}} \)
\(\displaystyle \epsilon \approx 7.958 \times 10^{-7} \)
So, the stress produced in the wire is approximately (159154.943 N/m2) and the strain produced is \(\displaystyle 7.958 \times 10^{-7}\).
Example 2: A copper wire of length (4, m) and diameter (2, mm) is stretched by a force of (300, N). If Young’s modulus of copper is \(\displaystyle 1.2 \times 10^{11} \), N/m2, calculate the stress and strain produced in the wire.
Solution: Given;
- Length of the wire, (L = 4, m)
- Diameter of the wire, (d = 2, mm = 0.002, m)
- Applied force, (F = 300, N)
- Young’s modulus of copper, \(\displaystyle Y = 1.2 \times 10^{11} \, N/m^2\)
First, we find the cross-sectional area of the wire:
\(\displaystyle A = \frac{\pi d^2}{4} \)
\(\displaystyle A = \frac{\pi \times (0.002)^2}{4} \)
\(\displaystyle A = \frac{\pi \times 0.000004}{4} \)
\(\displaystyle A = \frac{\pi}{1000000} \, m^2 \)
Now, we can calculate the stress (σ) using the formula:
\(\displaystyle \sigma = \frac{F}{A} \)
\(\displaystyle \sigma = \frac{300}{\frac{\pi}{1000000}} \)
\(\displaystyle \sigma = \frac{300 \times 1000000}{\pi} \, N/m^2 \)
\(\displaystyle \sigma \approx 95492.509 \, N/m^2 \)
Next, we calculate the strain (\(\displaystyle\epsilon\)) using Hooke’s law:
\(\displaystyle \epsilon = \frac{\sigma}{Y} \)
\(\displaystyle \epsilon = \frac{95492.509}{1.2 \times 10^{11}} \)
\(\displaystyle \epsilon \approx 7.958 \times 10^{-7} \)
So, the stress produced in the wire is approximately (95492.509 , N/m2) and the strain produced is \(\displaystyle7.958 \times 10^{-7}\).
Example 3: A rubber block of dimensions \(\displaystyle10 \, cm \times 5 \, cm \times 2 \, cm\) is subjected to a compressive force of (400 \, N). If Young’s modulus of rubber is \(\displaystyle 5 \times 10^6 \, N/m^2\), calculate the stress and strain produced in the rubber block.
Solution: Given;
- Dimensions of the rubber block: \(\displaystyle10 \, cm \times 5 \, cm \times 2 \, cm\)
- Applied force, (F = 400 , N)
- Young’s modulus of rubber, \(\displaystyle Y = 5 \times 10^6 \, N/m^2\)
First, we need to find the cross-sectional area of the block:
\(\displaystyle A = 10 \times 5 \, cm^2 = 50 \, cm^2 = 0.005 \, m^2 \)
Now, we can calculate the stress (σ):
\(\displaystyle \sigma = \frac{F}{A} = \frac{400}{0.005} = 80000 \, N/m^2 \)
Next, we calculate the strain (\(\displaystyle\epsilon\)) using Hooke’s law:
\(\displaystyle \epsilon = \frac{\sigma}{Y} = \frac{80000}{5 \times 10^6} = 0.016 \)
So, the stress produced in the rubber block is (80000, N/m2) and the strain produced is (0.016).
Example 4: A steel rod of length (1, m) and diameter (2, cm) is subjected to a tensile force of (1000, N). If Young’s modulus of steel is \(\displaystyle 2 \times 10^{11} \, N/m^2\), calculate the stress and strain produced in the rod.
Solution: Given;
- Length of the rod, (L = 1, m)
- Diameter of the rod, (d = 2, cm = 0.02, m)
- Applied force, (F = 1000, N)
- Young’s modulus of steel, \(\displaystyle Y = 2 \times 10^{11} \, N/m^2\)
First, we need to find the cross-sectional area of the rod:
\(\displaystyle A = \frac{\pi d^2}{4} = \frac{\pi (0.02)^2}{4} = \frac{\pi \times 0.0004}{4} = \frac{\pi}{10000} \, m^2 \)
Now, we can calculate the stress (σ):
\(\displaystyle \sigma = \frac{F}{A} = \frac{1000}{\frac{\pi}{10000}} = \frac{10000 \times 10000}{\pi} \, N/m^2 \approx 318309.886 \, N/m^2 \)
Next, we calculate the strain ((\epsilon)) using Hooke’s law:
\(\displaystyle \epsilon = \frac{\sigma}{Y} = \frac{318309.886}{2 \times 10^{11}} \approx 1.591 \times 10^{-6} \)
So, the stress produced in the rod is approximately (318309.886, N/m2) and the strain produced is \(\displaystyle1.591 \times 10^{-6}\).
Example 5: A copper wire of length (2, m) and diameter (1, mm) is stretched by a force of (400, N). If Young’s modulus of copper is \(\displaystyle 1.2 \times 10^{11} \, N/m^2\), calculate the stress and strain produced in the wire.
Solution: Given;
- Length of the wire, (L = 2, m)
- Diameter of the wire, (d = 1, mm = 0.001, m)
- Applied force, (F = 400, N)
- Young’s modulus of copper, \(\displaystyle Y = 1.2 \times 10^{11} \, N/m^2\)
First, we find the cross-sectional area of the wire:
\(\displaystyle A = \frac{\pi d^2}{4} = \frac{\pi (0.001)^2}{4} = \frac{\pi \times 0.000001}{4} = \frac{\pi}{4000000} \, m^2 \)
Now, we can calculate the stress (σ):
\(\displaystyle \sigma = \frac{F}{A} = \frac{400}{\frac{\pi}{4000000}} = \frac{400 \times 4000000}{\pi} \, N/m^2 \approx 318309.886 \, N/m^2 \)
Next, we calculate the strain (\(\displaystyle\epsilon\)) using Hooke’s law:
\(\displaystyle\epsilon = \frac{\sigma}{Y} = \frac{318309.886}{1.2 \times 10^{11}} \approx 2.652 \times 10^{-6} \)
So, the stress produced in the wire is approximately (318309.886, N/m2) and the strain produced is \(\displaystyle 2.652 \times 10^{-6}\).
Example 6: A rubber block of dimensions \(\displaystyle 15 \, cm \times 10 \, cm \times 5 \, cm\) is subjected to a compressive force of (600, N). If Young’s modulus of rubber is \(\displaystyle 4 \times 10^6 \, N/m^2\), calculate the stress and strain produced in the rubber block.
Solution: Given;
- Dimensions of the rubber block: \(\displaystyle15 \, cm \times 10 \, cm \times 5 \, cm\)
- Applied force, (F = 600, N)
- Young’s modulus of rubber, \(\displaystyle Y = 4 \times 10^6 \, N/m^2\)
First, we need to find the cross-sectional area of the block:
\(\displaystyle A = 15 \times 10 \, cm^2 = 150 \, cm^2 = 0.015 \, m^2 \)
Now, we can calculate the stress (σ):
\(\displaystyle \sigma = \frac{F}{A} = \frac{600}{0.015} = 40000 \, N/m^2 \)
Next, we calculate the strain (\(\displaystyle\epsilon\)) using Hooke’s law:
\(\displaystyle\epsilon = \frac{\sigma}{Y} = \frac{40000}{4 \times 10^6} = 0.01 \)
So, the stress produced in the rubber block is (40000, N/m2) and the strain produced is (0.01).
FAQs
What is the fundamental difference between stress and strain in the context of material physics?
Stress is the measure of the force applied per unit area of a material, indicating how much internal resistance the material offers against deformation. Strain, on the other hand, is the measure of deformation experienced by a material relative to its original size or shape when subjected to stress. In essence, stress represents the force applied, while strain represents the material’s response to that force.
How does the elastic modulus vary among different materials, and what does it signify?
Elastic modulus, often referred to as Young’s Modulus, varies significantly among different materials and is a fundamental property used to characterize a material’s stiffness or rigidity. Higher values of elastic modulus indicate stiffer materials that require more stress to produce a given amount of strain, whereas lower values signify more flexible materials.
Can you explain the concept of shear stress and its significance in material behavior?
Shear stress occurs when forces act parallel to the surface of a material, causing adjacent layers to slide past each other. It’s crucial to understand how materials deform under torsional or shear loading conditions. Shear stress is calculated as the force applied parallel to the surface divided by the area over which it’s applied.
How does the yield point relate to the stress-strain curve, and why is it important?
The yield point is the stress at which a material begins to exhibit plastic deformation, meaning it undergoes permanent changes in shape or size. On a stress-strain curve, it marks the transition from elastic to plastic behavior. Understanding the yield point is crucial for determining a material’s strength and designing structures to avoid permanent deformation.
What role does the ultimate tensile strength play in material engineering?
Ultimate tensile strength (UTS) is the maximum stress a material can withstand before fracturing or breaking under tension. It’s a critical parameter in material selection for engineering applications, as it indicates the material’s ability to withstand extreme loading conditions without failure. Materials with high UTS are preferred for applications requiring strength and durability.
How does strain hardening affect the behavior of materials under repeated loading?
Strain hardening, also known as work hardening, occurs when a material becomes stronger and less ductile due to plastic deformation. This phenomenon typically happens during repeated loading cycles, where the material undergoes incremental increases in strength. While strain hardening improves a material’s resistance to deformation, it may also lead to brittleness in some cases.
Can you explain the concept of engineering stress and engineering strain, and why are they used instead of true stress and true strain in practical applications?
Engineering stress and strain are calculated based on the original dimensions of a material, disregarding any changes in cross-sectional area or length during deformation. They provide a simplified approach for analyzing material behavior in engineering applications. True stress and strain, on the other hand, consider the instantaneous dimensions of the material, offering a more accurate representation but requiring complex measurements. In practical applications, engineering stress and strain are often used for their simplicity and ease of calculation.