Structure of Nucleus

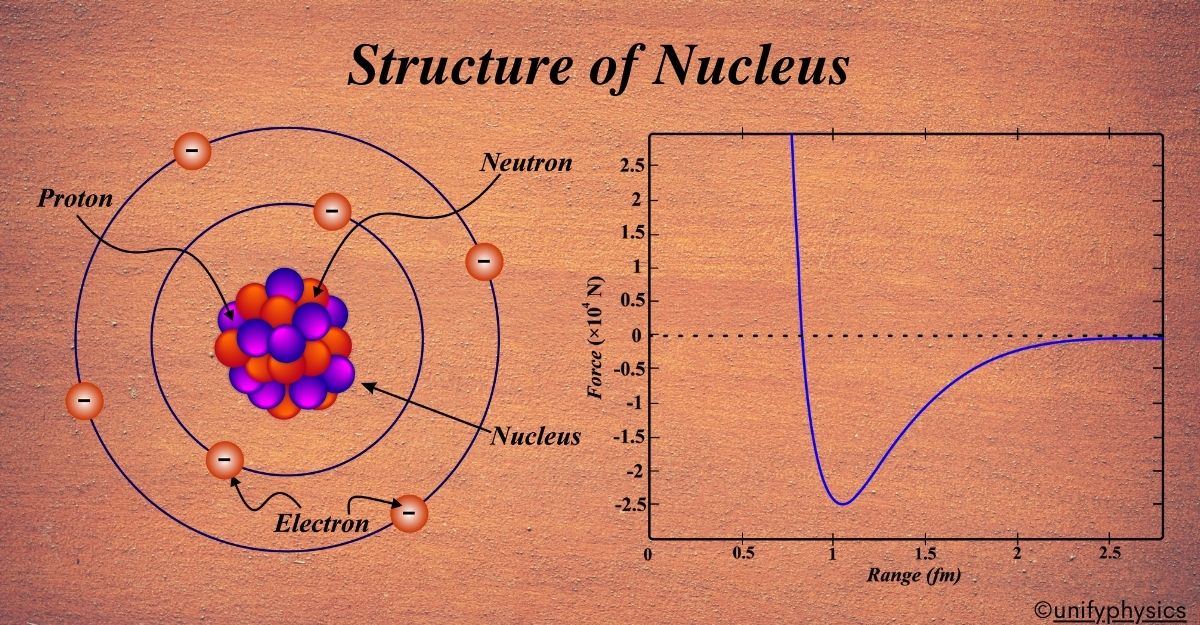
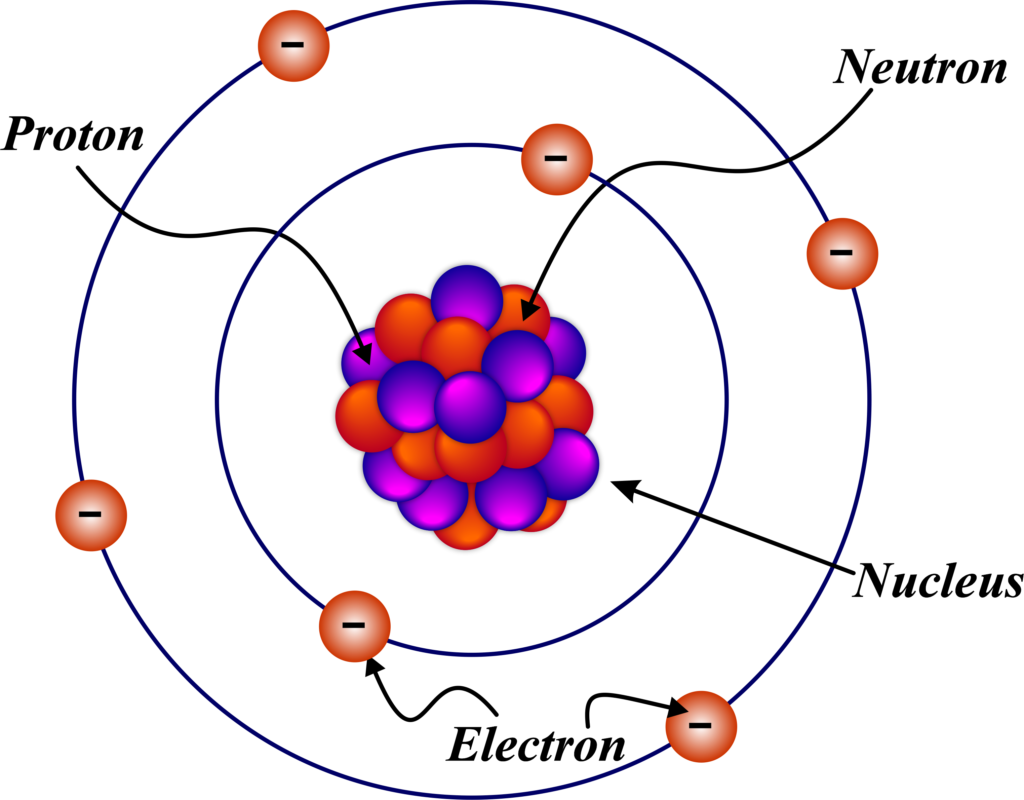
The journey into the heart of the atom began with Ernest Rutherford. In 1911, he proposed the nuclear model of the atom, which was a groundbreaking shift from the earlier plum pudding model suggested by J.J. Thomson. Rutherford’s model came as a result of the famous Gold Foil Experiment conducted by Hans Geiger and Ernest Marsden in 1909.

In this experiment, Rutherford directed a beam of alpha particles at a thin sheet of gold foil. He expected the particles to pass through with little deflection, as predicted by the plum pudding model. However, while most particles did pass straight through, some were deflected at large angles, and a few even bounced back.

Rutherford concluded that these observations could only be explained if the positive charge and most of the mass of the atom were concentrated in a tiny central core, which he called the nucleus. This nucleus was surrounded by a cloud of negatively charged electrons that occupied the rest of the atom’s volume.

Later, it was discovered that the nucleus is made up of protons, which carry a positive charge, and neutrons, which are neutral. This discovery was crucial because it explained why atoms didn’t collapse under electrostatic forces; the neutrons helped to buffer the repulsive forces between protons.

Rutherford’s discovery of the nucleus paved the way for the development of nuclear physics. It led to the understanding of nuclear forces, the discovery of the neutron by James Chadwick in 1932, and eventually the exploration of nuclear fission and fusion.

Terminology Related to the Nucleus of an Atom

Atomic Number (Z): The atomic number is denoted by (Z ) and represents the number of protons in the nucleus. It’s unique to each element and determines the element’s identity in the periodic table. For example, carbon has an atomic number of 6, which means every carbon nucleus has 6 protons.

Nucleons: Nucleons are the particles found in the nucleus, encompassing both protons and neutrons. They are held together by the strong nuclear force, which is much stronger than the electromagnetic force repelling the positively charged protons.

Atomic Mass Unit (u): The atomic mass unit is a standard unit of mass that quantifies atomic and molecular scale masses. One atomic mass unit is defined as one-twelfth the mass of a carbon-12 atom, approximately ( 1.66 × 10^-27) kilograms.

Nuclides: A nuclide is a specific type of nucleus characterized by its number of protons and neutrons. The term encompasses all the different possible nuclei of every element.

Radioactivity: Radioactivity is a phenomenon where unstable nuclei lose energy by emitting radiation. There are three main types of radioactive decay: alpha (α), beta (β), and gamma (γ) decay. Each type involves the nucleus releasing particles or energy to become more stable.

Alpha Particles: Alpha particles consist of two protons and two neutrons bound together. They are emitted from the nucleus during alpha decay, which typically occurs in very heavy elements.

Beta Particles: Beta particles are high-energy, high-speed electrons or positrons emitted by certain types of radioactive nuclei such as potassium-40. Beta decay can occur in two forms: (β^–) decay where a neutron turns into a proton and an electron, and (β⁺) decay where a proton turns into a neutron and a positron.

Gamma Rays: Gamma rays are high-frequency electromagnetic waves emitted from the nucleus. They often accompany alpha and beta decay, carrying away the excess energy from the nucleus.

Types of Nuclei

The nucleus of an atom can vary in its composition, leading to different types of nuclei. Here are the main categories:

Isotopes:

Isotopes are variants of a particular chemical element that have the same number of protons (and hence the same atomic number) but different numbers of neutrons. This means that while they are the same element, they have different mass numbers.

All isotopes of an element share the same chemical properties because they have the same number of electrons. However, their physical properties may differ due to the difference in mass. Most elements exist as a mixture of isotopes. For example, carbon naturally occurs mainly as Carbon-12 and Carbon-13, with a trace amount of Carbon-14.

Isotopes are often denoted by the element’s symbol followed by the mass number. For instance, the isotopes of hydrogen are protium (¹H), deuterium (²H), and tritium (³H), where the superscript indicates the mass number (the total number of protons and neutrons).

Examples:

• Carbon Isotopes: Carbon-12 has 6 protons and 6 neutrons, Carbon-13 has 6 protons and 7 neutrons, and Carbon-14 has 6 protons and 8 neutrons. Carbon-14 is radioactive and is used in radiocarbon dating.
• Hydrogen Isotopes: The most common isotope of hydrogen, protium, has no neutrons, deuterium has one neutron, and tritium has two neutrons. Tritium is also radioactive.

Some isotopes are unstable and radioactive. These isotopes can be used in medical treatments, as tracers in biological and chemical research, and in dating ancient objects. Stable isotopes do not undergo radioactive decay and are used in various scientific applications, including climate studies and forensic analysis.

Isobars:

Isobars are nuclei that have the same mass number but different atomic numbers. This means they have the same total number of protons and neutrons, but the distribution between these two types of nucleons is different.

The mass number (A) is the sum of the number of protons (Z) and the number of neutrons (N) in the nucleus. Isobars have the same mass number. Even though isobars have the same mass number, they are different chemical elements because they have different numbers of protons.

Example: An example of isobars would be Argon-40 (18 protons and 22 neutrons) and Calcium-40 (20 protons and 20 neutrons). Both have a mass number of 40 but differ in their atomic numbers.

Isobars can have different stabilities. Some may be stable, while others may be radioactive. Understanding isobars is important in nuclear chemistry and physics, as different isobars can participate in or result from nuclear reactions.

Isotones:

Isotones are nuclei that have the same number of neutrons but different numbers of protons. This means that while they have different atomic numbers and potentially belong to different elements, they share a common neutron count.

The defining characteristic of isotones is their neutron number. It remains constant across isotones. Isotones are not the same element, as their number of protons (and hence their atomic number) varies. This difference in proton number makes them distinct elements on the periodic table.

Example: An example of isotones would be Carbon-14 (6 protons and 8 neutrons) and Nitrogen-15 (7 protons and 8 neutrons). Both have 8 neutrons but differ in their proton count.

Isotones can provide insights into nuclear stability. Nuclei with the same number of neutrons can have different stability levels based on their proton count. Isotones are important in the study of nuclear reactions, especially in understanding how changes in neutron number affect nuclear properties.

Mirror Nuclei:

Mirror nuclei are pairs of nuclei where the number of protons in one nucleus is equal to the number of neutrons in the other, and vice versa. These pairs of nuclei have the same mass number but opposite proton and neutron numbers. Although the proton and neutron numbers are reversed, mirror nuclei have the same mass number because the sum of protons and neutrons remains constant.

In mirror nuclei, the number of protons in one nucleus is the same as the number of neutrons in its mirror counterpart. Mirror nuclei pairs have equal spins and the same parity, which means they share similar nuclear properties.

Examples:

• Carbon-14 and Oxygen-14: Carbon-14 has 6 protons and 8 neutrons, while Oxygen-14 has 8 protons and 6 neutrons. They are mirror nuclei because the proton number of one is the neutron number of the other.
• Nitrogen-15 and Oxygen-15: Nitrogen-15 has 7 protons and 8 neutrons, and Oxygen-15 has 8 protons and 7 neutrons. They also form a pair of mirror nuclei.

Isomer Nuclei:

Isomer nuclei are nuclei that have the same atomic number and mass number but exist in different energy states. This means they are the same element, with the same number of protons and neutrons, but their internal arrangements are different, leading to different energy levels.

Isomer nuclei belong to the same element because they have the same number of protons. Despite having the same atomic and mass numbers, isomer nuclei have different nuclear energy states. This can affect their nuclear properties, such as their stability and the way they decay. Some isomer nuclei are in metastable states, meaning they are not in the lowest possible energy state and can release energy as they transition to a more stable state.

Example: A common example of an isomer nucleus used in medical imaging is Technetium-99m. It has the same number of protons and neutrons as Technetium-99 but is in a higher energy state. It emits gamma rays as it decays to the lower energy state of Technetium-99.

Size of the Nucleus

The nucleus is incredibly small compared to the overall size of the atom. If we compare the size of the nucleus to the size of the atom, the nucleus is much smaller. The radius of a nucleus is about 10,000 times smaller than the radius of an atom.

Because of this vast difference in size, the volume of the nucleus is about 10^-12 times the volume of the atom. This means that the atom is mostly empty space. The size of the nucleus was first estimated through Rutherford’s gold foil experiment. By observing the scattering of alpha particles, scientists concluded that the nucleus occupies a very small portion of the atom’s volume.

The typical nuclear radius can be estimated using the formula

\(\displaystyle R = R_0 A^{1/3} \)

where (R₀) is a constant approximately equal to \(\displaystyle 1.2 \times 10^{-15} \text{m}\) and (A) is the atomic mass number, which is the total number of protons and neutrons in the nucleus.

We know that the volume of a sphere is given by ( \(\displaystyle\frac{4}{3}\pi r^3 \)), and the volume of the nucleus is proportional to the number of nucleons it contains. If we assume that each nucleon occupies roughly the same volume, then the volume of the nucleus should be proportional to the mass number (A).

Combining these ideas, we get:

\(\displaystyle \text{Volume of nucleus} = \frac{4}{3}\pi R^3 = kA \)

where (k) is a proportionality constant. To find (R), we rearrange the equation:

\(\displaystyle R^3 = \frac{3kA}{4\pi} \)

We introduce (R₀), which is defined such that (k) is absorbed into (R₀), and (R³₀ ) represents the volume occupied by one nucleon.

Therefore, we have:

\(\displaystyle R = R_0 A^{1/3} \)

This formula tells us that the radius of the nucleus increases with the cube root of the mass number, which means that as you add more nucleons, the nucleus gets bigger, but at a slower rate than the number of nucleons being added.

Density of Nucleus

The density of the nucleus is incredibly high due to its small size and the mass it contains. The density of a nucleus refers to its mass per unit volume. Despite the variety in size and mass of different nuclei, the density of nuclear matter is remarkably consistent across all nuclei.

The reason behind this uniform density is the nature of the strong nuclear force, which binds nucleons (protons and neutrons) together. This force works over a very short range and is independent of the type of nucleon. As a result, the nucleons are packed together in roughly the same density, no matter the size of the nucleus.

To give you an idea of how dense the nucleus is, consider this: if an object had the same density as a nucleus, a cube of it with sides measuring just 1 centimeter would weigh about 230 billion tonnes! That’s because the nuclear density is approximately (\(\displaystyle 2.3 \times 10^{17} \)) kg/m. Imagine squeezing the mass of a cruise ship into a volume as small as a sugar cube. That’s how dense the nucleus is. It’s this incredible density that makes the nucleus the tiny yet massive heart of the atom.

Density is defined as mass per unit volume. For a nucleus, we can express this as:

\(\displaystyle \text{Density} (\rho) = \frac{\text{Mass of nucleus}}{\text{Volume of nucleus}} \)

The mass of the nucleus is approximately equal to the mass number (A), which is the total number of protons and neutrons, as each nucleon (proton or neutron) has a mass of about 1 atomic mass unit (u).

The nucleus can be approximated as a sphere, and the volume of a sphere is given by:

\(\displaystyle V = \frac{4}{3}\pi r^3 \)

where (r) is the radius of the nucleus.

The radius of a nucleus is related to the mass number (A) by the empirical formula:

\(\displaystyle r = r_0 A^{1/3} \)

where (r₀) is a constant with a value of about (\(\displaystyle 1.2 \times 10^{-15} \)) meters.

Now, let’s put it all together. Substituting the expression for the radius into the volume formula, we get:

\(\displaystyle V = \frac{4}{3}\pi (r_0 A^{1/3})^3 \)

Simplifying, we find:

\(\displaystyle V = \frac{4}{3}\pi r_0^3 A \)

Now, substituting the expressions for mass and volume into the density equation, we have:

\(\displaystyle \rho = \frac{A \times 1 \text{ u}}{\frac{4}{3}\pi r_0^3 A} \)

Notice that the mass number (A) cancels out, leaving us with:

\(\displaystyle \rho = \frac{1 \text{ u}}{\frac{4}{3}\pi r_0^3} \)

Since 1 u is approximately (\(\displaystyle 1.66 \times 10^{-27} \)) kg and (r₀) is (\(\displaystyle 1.2 \times 10^{-15} \)) meters, we can calculate the numerical value for the density of the nucleus.

The final expression for the density of the nucleus is:

\(\displaystyle \rho = \frac{1.66 \times 10^{-27} \text{ kg}}{\frac{4}{3}\pi (1.2 \times 10^{-15} \text{ m})^3} \)

When you calculate this, you’ll find that the density of the nucleus is incredibly high, on the order of (\(\displaystyle 10^{17} \)) kg/m³, which is consistent across different nuclei. This derivation shows that the density of the nucleus is independent of the mass number (A), which is a fascinating aspect of nuclear physics.

Mass Defect

The mass defect is the difference between the mass of a nucleus and the sum of the masses of its individual nucleons. This difference is due to the binding energy that holds the nucleus together. Imagine you have a bunch of Lego blocks. Individually, each block has its own weight. Now, when you put them together to build a structure, you’d expect the total weight to be the sum of all the individual blocks, right? Surprisingly, in the atomic world, that’s not the case.

When protons and neutrons (which we can think of as atomic Lego blocks) come together to form a nucleus, the total mass of the nucleus is less than the sum of the masses of the individual protons and neutrons if they were separate. This missing mass is what we call the mass defect.

The mass defect occurs because when nucleons join to form a nucleus, some of their mass is converted into energy. This energy is what glues the nucleons together in the nucleus, known as the binding energy. It’s like paying a portion of the Lego blocks as a fee to stick together, and that fee is paid in the form of mass.

To calculate the mass defect, we use the formula:

\(\displaystyle \Delta m = (Zm_p + Nm_n) – M \)

• (∆ m) is the mass defect.
• (Z) is the number of protons.
• (m_p) is the mass of a proton.
• (N) is the number of neutrons.
• (m_n) is the mass of a neutron.
• (M) is the measured mass of the nucleus.

The mass defect tells us how much energy is holding the nucleus together. A larger mass defect means more energy is used to bind the nucleus, which usually indicates a more stable nucleus.

Example: Let’s say we have a helium nucleus with 2 protons and 2 neutrons. The predicted mass would be:

\(\displaystyle \text{Predicted Mass} = (2 \times 1.00728 \, \text{amu}) + (2 \times 1.00867 \, \text{amu}) \)

If the actual mass of the helium nucleus is found to be (4.00260 amu), then the mass defect would be:

\(\displaystyle \Delta M = (2 \times 1.00728 \, \text{amu}) + (2 \times 1.00867 \, \text{amu}) – 4.00260 \, \text{amu} \)

By calculating this, we can find the mass defect and understand that this ‘missing’ mass (0.0293 amu) is what has been converted into binding energy, holding the nucleus together.

Mass-Energy Equivalence Relation

The mass-energy equivalence is a fundamental principle of physics introduced by Albert Einstein. It tells us that mass and energy are two forms of the same thing and can be converted into each other. This is expressed in the famous equation:

\(\displaystyle E = mc^2 \)

E stands for energy, m represents mass, and c is the speed of light in a vacuum, which is about (3 × 10⁸) meters per second.

Imagine you have a tiny bit of matter, like a grain of sand. According to Einstein’s equation, if you could convert that entire grain of sand into pure energy, it would release an enormous amount of energy. That’s because the speed of light (c) is such a large number, and when you square it, it becomes huge!

This relation is crucial because it explains how the Sun and other stars produce energy. In the core of stars, hydrogen atoms fuse together to form helium, and some of their mass is converted into energy, lighting up the stars and providing warmth to planets like ours.

The equation also implies that a small amount of mass can be converted into a very large amount of energy, which is the principle behind nuclear power and atomic bombs. It’s a clear demonstration of how even a little mass contains a vast store of energy.

Also Read: Atomic Mass and Composition of Nucleus

Nuclear Force

The nuclear force is a strong force that acts between nucleons, overcoming the electrostatic repulsion between protons to keep the nucleus stable. The nuclear force, also known as the strong force, is one of the four fundamental forces of nature. It’s the glue that holds the nucleus of an atom together. Without it, the nucleus, which contains positively charged protons and neutral neutrons, would fly apart due to the repulsive electromagnetic force between the like-charged protons.

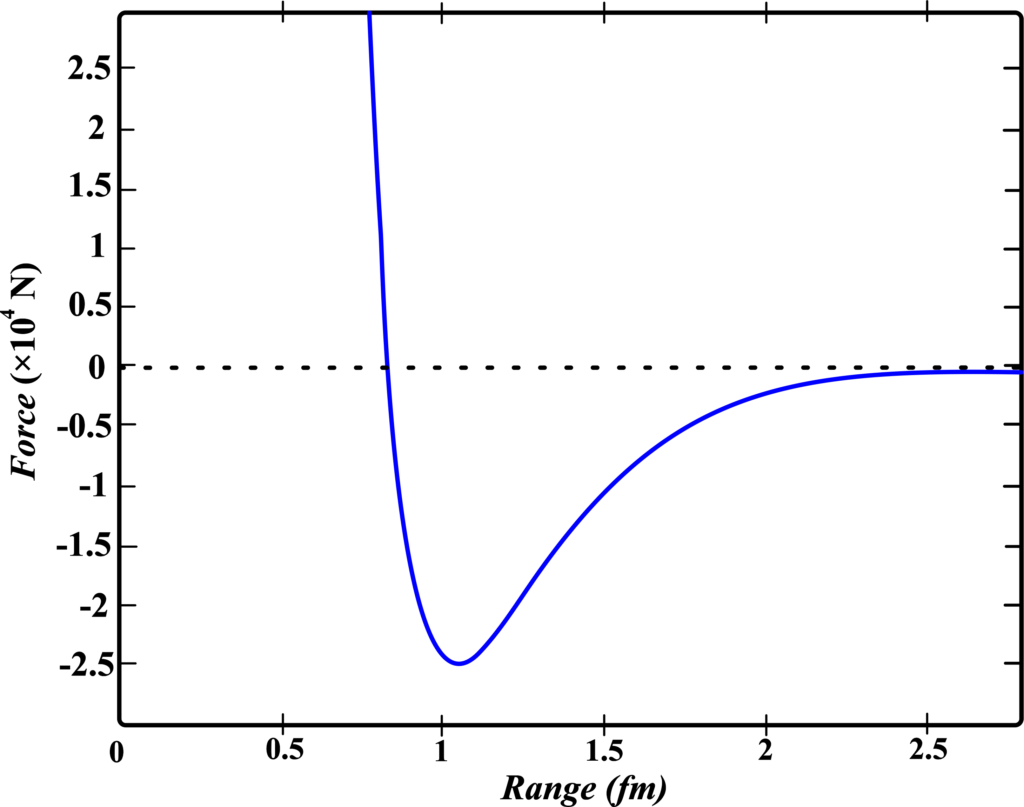
The nuclear force is incredibly strong, much stronger than the electromagnetic force that it needs to overcome. It’s about 10 million times stronger than the chemical binding forces that hold molecules together.

One of the most interesting things about the nuclear force is that it’s a short-range force. It’s extremely powerful at distances of about 1 femtometer (which is (\(\displaystyle 1 \times 10^{-15}\)) meters), but beyond 2.5 femtometers, its strength decreases rapidly.

Properties of Nuclear Force:

• Strength of Nuclear Force: The nuclear force is significantly stronger than both the Coulomb force, which acts between charged particles, and the gravitational force, which acts between masses. This superior strength allows the nuclear force to overcome the repulsive Coulomb force between the positively charged protons within the nucleus.
• Range and Saturation: The nuclear force has a very short range, dropping off rapidly beyond a few femtometers. Due to this, the force doesn’t increase indefinitely with more nucleons, leading to a consistent binding energy per nucleon in larger nuclei.
• Behavior at Different Distances: The potential energy between two nucleons is lowest at a distance of about 0.8 femtometers, indicating an attractive force at larger distances and a repulsive force at shorter distances.
• Charge Independence: The nuclear force is approximately equal whether it’s between two neutrons, a proton and a neutron, or two protons, showing that it doesn’t depend on the electric charge of the particles involved.

The nuclear force is the critical factor that allows nuclei to exist despite the repulsive forces between protons, and it operates in a way that is independent of the electric charge of the nucleons. Without the nuclear force, the universe as we know it wouldn’t exist.

Binding Energy

The binding energy is the energy required to disassemble a nucleus into its individual nucleons. It’s equivalent to the energy released when a nucleus is formed from separate nucleons. Binding energy is like the “glue” that holds the nucleus of an atom together. It’s the energy needed to break the nucleus into its individual protons and neutrons.

Protons are positively charged, and like charges repel each other. So, without something to keep them together, the nucleus would just fly apart. Binding energy is the force that overcomes this repulsion and keeps the nucleus intact.

When protons and neutrons come together to form a nucleus, they release energy. This released energy is the binding energy. It’s a bit like when you snap two magnets together; they stick because releasing energy makes the system more stable.

According to Einstein’s famous equation (\(\displaystyle E = mc^2 \)), mass can be converted into energy. When nucleons form a nucleus, some of their mass is converted into binding energy. This loss of mass is called the mass defect, and it’s what gives us the binding energy.

To find the binding energy, you calculate the mass defect first and then use Einstein’s equation to convert that mass into energy. The formula looks like this:

\(\displaystyle E_b = (\Delta m)c^2 \)

where (E_b) is the binding energy, (∆m) is the mass defect, and (c) is the speed of light.

The amount of binding energy tells us how stable a nucleus is. A higher binding energy means a more stable nucleus. It’s like a stronger glue holding everything together.

Binding Energy Per Nucleon

It’s the average energy needed to remove a single nucleon (either a proton or a neutron) from a nucleus. Think of it like the average breakup cost for taking one member out of a tightly-knit group. Measuring the binding energy for the whole nucleus doesn’t give us a fair comparison between different nuclei because they can have different numbers of nucleons. By looking at the energy per nucleon, we can compare how tightly bound nucleons are in different nuclei, regardless of their size.

To calculate the binding energy per nucleon, we take the total binding energy of the nucleus (which is the energy released when the nucleus is formed from individual protons and neutrons) and divide it by the number of nucleons in the nucleus.

The formula looks like this:

\(\displaystyle \text{Binding Energy per Nucleon} = \frac{\text{Total Binding Energy}}{\text{Number of Nucleons}} \)

A higher binding energy per nucleon means a more stable nucleus. Elements like iron have a high binding energy per nucleon, which is why they are so stable. On the other hand, elements with a lower binding energy per nucleon are less stable and more likely to undergo radioactive decay.

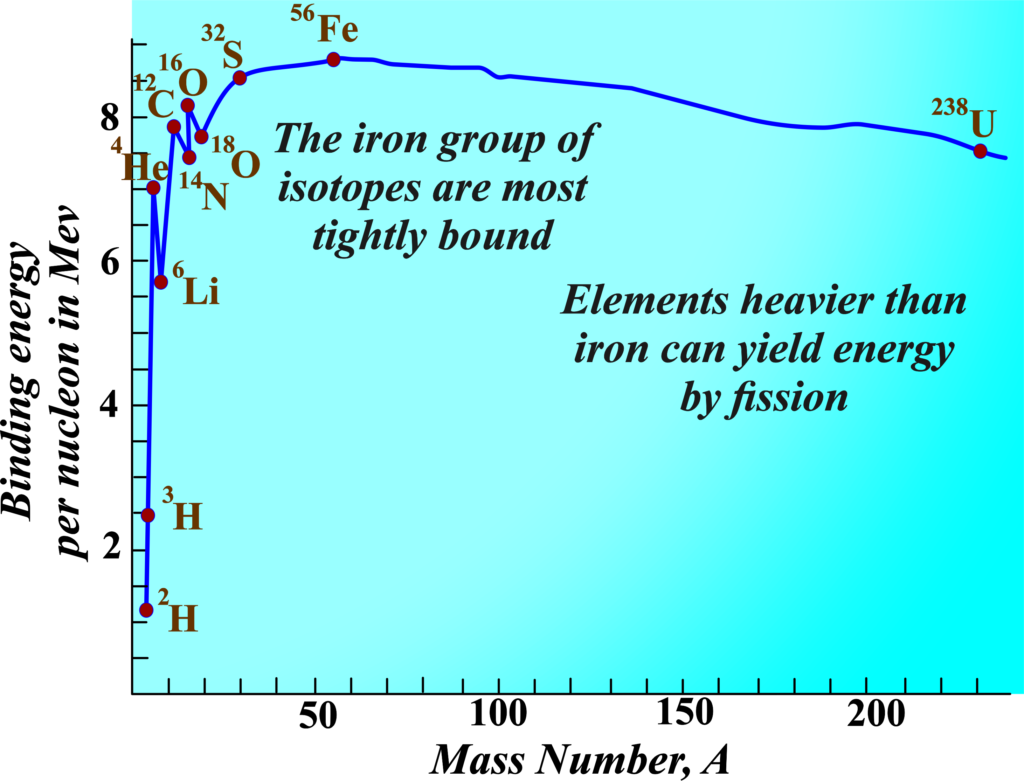
The Curve:

When we plot the binding energy per nucleon against the number of nucleons, we get a curve that peaks around elements like iron. This curve tells us that lighter and heavier nuclei are less tightly bound compared to mid-sized ones like iron.

• Stability of Middle-Size Nuclei: For nuclei with a mass number between 30 and 170, the binding energy per nucleon remains fairly constant, around 8.75 MeV for nuclei like iron (A = 56) and 7.6 MeV for uranium (A = 238).
• Variation in Binding Energy: Lighter nuclei (with A < 30) and heavier nuclei (with A > 170) have lower binding energy per nucleon, indicating they are less tightly bound compared to mid-sized nuclei.
• The nuclear force is short-ranged, affecting only the immediate neighbors within a nucleus. This leads to a saturation effect, where adding more nucleons doesn’t significantly change the binding energy per nucleon for large nuclei.
• In very heavy nuclei, like those with A = 240, the binding energy per nucleon is lower than in mid-sized nuclei. If such a heavy nucleus splits into two mid-sized nuclei, the process releases energy because the resulting nuclei are more tightly bound.
• Conversely, when two very light nuclei combine to form a heavier nucleus, the binding energy per nucleon increases, and the new nucleus is more stable, releasing energy during fusion.

The binding energy per nucleon is a key indicator of nuclear stability and plays a crucial role in nuclear reactions, such as fusion and fission.

Solved Examples

Problem 1: Calculate the mass defect and binding energy of the helium-4 nucleus (\(\displaystyle ^4_2\text{He}\)). The atomic mass of helium-4 is 4.002602 u. The masses of a proton and a neutron are 1.007276 u and 1.008665 u, respectively.

Solution: First, calculate the total mass of the individual nucleons:

\(\displaystyle \text{Mass of 2 protons} = 2 \times 1.007276 \, \text{u} = 2.014552 \, \text{u} \)

\(\displaystyle \text{Mass of 2 neutrons} = 2 \times 1.008665 \, \text{u} = 2.017330 \, \text{u}\)

Total mass of individual nucleons:

\(\displaystyle m_{\text{nucleons}} = 2.014552 \, \text{u} + 2.017330 \, \text{u} = 4.031882 \, \text{u} \)

Mass defect:

\(\displaystyle \Delta m = m_{\text{nucleons}} – m_{\text{nucleus}} \)

\(\displaystyle \Delta m = 4.031882 \, \text{u} – 4.002602 \, \text{u} \)

\(\displaystyle \Delta m = 0.029280 \, \text{u} \)

Convert mass defect to energy (1 u = 931.5 MeV):

\(\displaystyle E = \Delta m \times 931.5 \, \text{MeV/u} \)

\(\displaystyle E = 0.029280 \times 931.5 \)

\(\displaystyle E \approx 27.26 \, \text{MeV} \)

The mass defect of the helium-4 nucleus is 0.029280 u, and the binding energy is approximately 27.26 MeV.

Problem 2: Calculate the binding energy per nucleon for the helium-4 nucleus (\(\displaystyle ^4_2\text{He}\)).

Solution: Using the total binding energy from Problem 1:

\(\displaystyle \text{Total binding energy} = 27.26 \, \text{MeV} \)

Number of nucleons:

\(\displaystyle \text{Number of nucleons} = 4 \)

Binding energy per nucleon:

\(\displaystyle \text{Binding energy per nucleon} = \frac{\text{Total binding energy}}{\text{Number of nucleons}} \)

\(\displaystyle \text{Binding energy per nucleon} = \frac{27.26 \, \text{MeV}}{4} \)

\(\displaystyle \text{Binding energy per nucleon} = 6.815 \, \text{MeV} \)

The binding energy per nucleon for helium-4 is approximately 6.815 MeV.

Problem 3: Calculate the radius of the gold nucleus (\(\displaystyle ^{197}_{79}\text{Au}\)) using the empirical formula (\(\displaystyle R = R_0 A^{1/3} \)), where (\(\displaystyle R_0 = 1.2 \times 10^{-15} \)) meters.

Solution: Given: A = 197 

\(\displaystyle R_0 = 1.2 \times 10^{-15} \, \text{meters} \)

Calculate the radius:

\(\displaystyle R = R_0 A^{1/3} \)

\(\displaystyle R = 1.2 \times 10^{-15} \times 197^{1/3} \)

\(\displaystyle R \approx 1.2 \times 10^{-15} \times 5.83 \)

\(\displaystyle R \approx 6.996 \times 10^{-15} \, \text{meters} \)

The radius of the gold nucleus is approximately (\(\displaystyle 6.996 \times 10^{-15} \)) meters.

Problem 4: Calculate the energy equivalent of 1 gram of mass using Einstein’s mass-energy equivalence relation (\(\displaystyle E = mc^2 \)).

Solution: Given; \(\displaystyle m = 1 \, \text{gram} = 10^{-3} \, \text{kg} \)

\(\displaystyle c = 3 \times 10^8 \, \text{m/s} \)

Calculate the energy:

\(\displaystyle E = mc^2 \)

\(\displaystyle E = 10^{-3} \times (3 \times 10^8)^2 \)

\(\displaystyle E = 10^{-3} \times 9 \times 10^{16} \)

\(\displaystyle E = 9 \times 10^{13} \, \text{J} \)

The energy equivalent of 1 gram of mass is (\(\displaystyle 9 \times 10^{13} \)) joules.

Problem 5: Given that the nuclear force is approximately 100 times stronger than the electromagnetic force, and the electromagnetic force between two protons is (\(\displaystyle 1.44 \times 10^{-9} \)) N, calculate the approximate strength of the nuclear force.

Solution: Given: \(\displaystyle F_{\text{electromagnetic}} = 1.44 \times 10^{-9} \, \text{N} \)

\(\displaystyle \text{Nuclear force is 100 times stronger} \)

Calculate the nuclear force:

\(\displaystyle F_{\text{nuclear}} = 100 \times F_{\text{electromagnetic}} \)

\(\displaystyle F_{\text{nuclear}} = 100 \times 1.44 \times 10^{-9} \)

\(\displaystyle F_{\text{nuclear}} = 1.44 \times 10^{-7} \, \text{N} \)

The approximate strength of the nuclear force is (\(\displaystyle 1.44 \times 10^{-7} \)) N.

Problem 6: Calculate the mass defect and binding energy of deuterium (\(\displaystyle ^2_1\text{H})\)). The atomic mass of deuterium is 2.014102 u. The masses of a proton and a neutron are 1.007276 u and 1.008665 u, respectively.

Solution: First, calculate the total mass of the individual nucleons:

\(\displaystyle \text{Mass of 1 proton} = 1.007276 \, \text{u} \)

\(\displaystyle \text{Mass of 1 neutron} = 1.008665 \, \text{u} \)

The total mass of individual nucleons:

\(\displaystyle m_{\text{nucleons}} = 1.007276 \, \text{u} + 1.008665 \, \text{u} = 2.015941 \, \text{u} \)

Mass defect:

\(\displaystyle \Delta m = m_{\text{nucleons}} – m_{\text{nucleus}} \)

\(\displaystyle \Delta m = 2.015941 \, \text{u} – 2.014102 \, \text{u} \)

\(\displaystyle\Delta m = 0.001839 \, \text{u} \)

Convert mass defect to energy (1 u = 931.5 MeV):

\(\displaystyle E = \Delta m \times 931.5 \, \text{MeV/u} \)

\(\displaystyle E = 0.001839 \times 931.5 \)

\(\displaystyle E \approx 1.714 \, \text{MeV} \)

The mass defect of deuterium is 0.001839 u, and the binding energy is approximately 1.714 MeV.

FAQs