The concept of surface energy has its roots in the observations and experiments of many scientists over the years. It’s a story of curiosity and discovery that spans centuries.
Long before the term “surface energy” was coined, people noticed that water behaved strangely at times. For example, water droplets form spheres, and some insects can walk on water without sinking. These observations hinted at some unseen force at work.
In the 18th century, scientists began to study these phenomena more systematically. Thomas Young and Pierre-Simon Laplace were among the first to describe the forces that act at the interfaces of liquids and gases, leading to the concept of surface tension.
The term “surface energy” itself was introduced to explain the work required to increase the surface area of a liquid or solid. It quantifies the disruption of intermolecular bonds that occurs when a surface is created. This was a significant step because it connected the macroscopic behavior of materials with the microscopic interactions between molecules.
Today, we understand that surface energy is a measure of the excess energy at the surface of a material compared to its bulk. When you cut a solid body into pieces, you disrupt bonds and increase the surface area, which increases the surface energy. This understanding helps us in various applications, from manufacturing to medicine.
With the advent of modern technology, scientists have developed methods to measure surface energy accurately. The contact angle method, for example, involves observing the angle at which a liquid droplet rests on a solid surface to calculate the surface energy.
What Is Surface Energy?
Surface energy is the work needed to increase the surface area of a material. Imagine stretching a rubber band; you work against the elastic forces. Similarly, when you create more surface area in a liquid, you work against the molecules’ cohesive forces.
Surface Energy is like the “skin” of a liquid or solid. Imagine you have a balloon. The rubber on the surface is stretched and under tension, right? That’s similar to surface energy. The energy exists at the surface of a material because the particles (like atoms or molecules) at the surface are not as tightly packed or bonded as those inside.
- Inside a Material: Particles are happy because they’re surrounded by friends (other particles) on all sides.
- At the Surface: Particles are a bit lonely because they have fewer neighbors. This makes them cling to their neighbors more strongly, creating a sort of ‘skin’ on the material.
For liquids, this ‘skin’ is what allows insects to walk on water and droplets to form beads on a car after it rains. For solids, it’s what makes materials like metals strong and able to hold their shape.
So, surface energy is the extra energy that these surface particles have because they’re not all surrounded by other particles. It’s a measure of how much work you’d have to do to break those stronger bonds at the surface to create more surface area.
Understanding Surface Energy through Water Droplets:
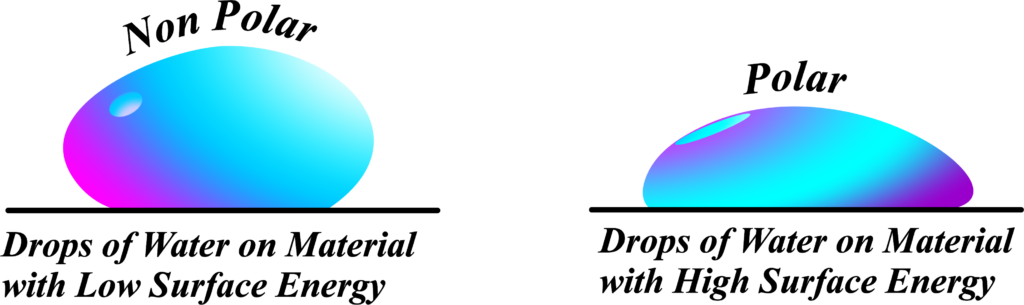
The image illustrates the behavior of water droplets on two different types of surfaces: one with low surface energy (nonpolar) and one with high surface energy (polar). This helps us understand how surface energy influences the shape and spreading of a liquid drop.
Low Surface Energy (Nonpolar Surface)
On the left side of the image, the water droplet is on a material with low surface energy. Because the surface is nonpolar, the cohesive forces within the water molecules are stronger than the adhesive forces between the water molecules and the surface. This causes the water droplet to form a more rounded shape, minimizing its contact area with the surface.
- Low Surface Energy: The material has weak adhesive forces with water.
- Nonpolar Surface: There is little to no attraction between the water and the surface.
- Droplet Shape: The droplet is more spherical, indicating strong cohesive forces within the water.
High Surface Energy (Polar Surface)
On the right side of the image, the water droplet is on a material with high surface energy. The surface is polar, which means it has strong adhesive forces with the water molecules. This causes the water to spread out more, forming a flatter droplet.
- High Surface Energy: The material has strong adhesive forces with water.
- Polar Surface: There is significant attraction between the water and the surface.
- Droplet Shape: The droplet spreads out, indicating strong adhesive forces with the surface.
On low surface energy (nonpolar) surfaces, water forms a rounded droplet due to stronger cohesive forces within the water. On high surface energy (polar) surfaces, water spreads out more due to stronger adhesive forces between the water and the surface.
This concept is crucial in various applications, such as coating technologies, painting, and waterproofing materials, where controlling the interaction between liquids and surfaces is essential.
Surface Energy Formula
When we talk about the Surface Energy Formula, we’re looking at how to calculate the amount of energy present on the surface of a material. It’s like figuring out how much energy it takes to create a new ‘skin’ on the material.
Here’s the formula in its simplest form:
\(\displaystyle \text{Surface Energy} (\gamma) = \frac{\text{Work Done} (W)}{\text{New Surface Area Created} (A)} \)
- Work Done (W): This is the energy you need to put in to stretch or break the material to create a new surface.
- New Surface Area Created (A): This is the extra area you’ve added to the surface by stretching or breaking it.
So, if you imagine blowing up a balloon, the work you do to blow air into the balloon is stretching the rubber and creating more surface area. The surface energy is the work done per unit area of that new balloon surface.
In mathematical terms, if you did 1 Joule of work to create 1 square meter of new surface, then the surface energy would be:
\(\displaystyle \gamma = \frac{1 \text{ Joule}}{1 \text{ m}^2} = 1 \text{ J/m}^2 \)
This formula helps us understand how much energy is stored on the surface of materials, which is super important in fields like material science, engineering, and even biology!
The surface energy is always positive because you’re putting energy into the system to create that new surface. It’s a fundamental concept that explains why materials behave the way they do at their boundaries.
Surface Energy Units and Dimensions
The SI unit of surface energy is Joules per square meter (J/m²), which can also be expressed as Newtons per meter.
| System of Units | Unit | Dimensions |
|---|---|---|
| S.I. | Newton/meter (N/m) | [M1L0T-2] |
| CGS | Dyne/centimeter (dyn/cm) | [M1L0T-2] |
| MKS | Kilogram-force/meter (kgf/m) | [M1L0T-2] |
Dimensions: This tells us what types of physical quantities are involved in measuring surface energy. The dimensions [M1L0T-2] mean that surface energy involves mass (M), no length (L), and is inversely related to the square of time (T).
This table should help you visualize and compare the different units and dimensions used to measure surface energy across various systems.
To put it simply, the units and dimensions of surface energy tell us about the ‘strength’ of the surface ‘skin’ of a material. It’s like measuring how much force is needed to stretch or break that ‘skin’ over a certain distance. Understanding these units and dimensions helps us compare the surface energy of different materials and predict how they will behave in various situations.
Free Energy on the Surface
Surface-free energy is the potential energy stored on the surface of a liquid due to the stretching of the surface. Free Energy on the Surface, also known as surface free energy or interfacial free energy, is the energy associated with the creation of a surface. It quantifies the disruption of intermolecular bonds when a new surface is formed.
Mathematically, the surface free energy (γ) is defined as the work (W ) required to create a unit area (A) of the surface without any volume change. The formula is:
\(\displaystyle \gamma = \frac{W}{A} \)
Now, let’s consider a liquid surface. The molecules at the surface have higher potential energy compared to those inside because they are not fully surrounded by other molecules. This extra potential energy is what we refer to as surface-free energy.
For a liquid, if we want to increase the surface area by a small amount (dA), we need to do work against the surface tension (σ). The work done (dW) is directly proportional to the surface tension and the change in area:
\(\displaystyle dW = \sigma \times dA \)
So, if we increase the surface area of a liquid by (dA), the increase in the free energy (dγ) is:
\(\displaystyle d\gamma = \sigma \times dA \)
This relationship shows that the surface tension is the force per unit length that must be overcome to increase the surface area, and the work done in overcoming this force is stored as surface-free energy.
Also Read: Bernoulli’s Principle
Relation Between Surface Energy and Surface Tension
Surface energy and surface tension are closely related. Surface tension is the force per unit length along the surface, which is responsible for the ‘skin-like’ behavior of liquids. The relation between them can be described as:
\(\displaystyle \text{Surface Energy} = \text{Surface Tension} \times \text{Change in Area} \)
Imagine you have a soap bubble. The bubble has a thin film of soap water that forms its surface. This film wants to shrink to the smallest possible size because of a force called surface tension. Now, if you want to make the bubble bigger, you need to work against this force.
Surface tension is the force that acts along the surface of a liquid, trying to minimize its area. It’s measured as the force per unit length. Surface energy, on the other hand, is the work done to increase the surface area of the liquid. It’s like the energy ‘cost’ of creating more surface.
Here’s the cool part: the work you do to stretch the bubble (which increases the surface area) is stored as surface energy. So, the more you stretch, the more surface energy you have.
The relation between them is pretty straightforward:
- When you increase the surface area by a tiny amount, the increase in surface energy is equal to the surface tension times the increase in area.
- In formula terms, it looks like this:
\(\displaystyle \text{Increase in Surface Energy} = \text{Surface Tension} \times \text{Increase in Area} \)
So, if the surface tension is like the ‘price per square meter’ of the surface, then the surface energy is the ‘total price’ you pay for the extra surface you create.
Surface tension is the ‘cost per unit area’ of creating a new surface, and surface energy is the total ‘cost’ for the entire new surface. They’re two sides of the same coin, and understanding this relationship helps us explain why liquids form droplets, why bubbles are spherical, and many other phenomena in nature.
Surface Tension and Surface Energy Relationship
Surface tension (σ) is directly proportional to surface energy (γ). The higher the surface energy of a liquid, the stronger the attractive forces between molecules at the surface, resulting in higher surface tension. Mathematically, the relationship is given by:
\(\displaystyle \sigma = \gamma \)
For liquids at their boiling points, surface tension and surface energy are closely related. Liquids with stronger intermolecular forces have higher surface energies and, consequently, higher surface tensions.
Excess Pressure Inside a Liquid Drop and a Bubble
A small water droplet maintains its shape due to surface tension. The surface tension can be defined by the formula:
\(\displaystyle \sigma = \frac{F}{L} \)
- (σ) is the surface tension of the liquid,
- (F) is the force acting per unit length,
- (L) is the length over which the force acts.
The fact that droplets don’t collapse indicates that the internal pressure (pi) inside the droplet is higher than the external pressure (po). The excess pressure (p) can be calculated as:
\(\displaystyle p = p_i – p_o \)
For a spherical droplet, the outside force is given by:
\(\displaystyle \text{Outside Force} = p \times \text{surface area of the drop} = (p_i – p_o) \times 4 \pi r^2 \)
where (r) is the radius of the droplet.
Calculating Work Done and Potential Energy
To increase the surface area of the droplet, the work done (dW) is:
\(\displaystyle dW = \text{Outside Force} = (p_i – p_o) \times 4 \pi r^2 \cdot dr \)
The work done by the excess pressure is stored as potential energy. The increase in potential energy (P.E.) due to surface tension is:
\(\displaystyle \text{Increase in P.E.} = \sigma \times \text{increase in surface area} \)
Considering a small increase in radius (dr):
\(\displaystyle \sigma \times [4 \pi (r + dr)^2 – 4 \pi r^2] = \sigma \times 8 \pi r \cdot dr \)
Thus,
\(\displaystyle dW = \text{Increase in P.E.} \)
Implies,
\(\displaystyle (p_i – p_o) \times 4 \pi r^2 \cdot dr = \sigma \times 8 \pi r \cdot dr \)
Simplifying,
\(\displaystyle (p_i – p_o) = \frac{2\sigma}{r} \)
Therefore, the excess pressure (p) inside a droplet is:
\(\displaystyle p = \frac{2\sigma}{r} \)
For bubbles, which have two free surfaces, like soap bubbles, the formula is:
\(\displaystyle p = \frac{4\sigma}{r} \)
When dealing with surfaces in contact with other materials (like fluids or solids), surface energy depends on how molecules interact across the interface. If the molecules attract each other, it lowers the surface energy. If they repel each other, it increases the surface energy.
Overall, surface energy should be thought of as the energetic state at the boundary between two different materials. It is influenced by the interaction and affinity between the molecules of both materials at the interface.
Solved Examples
Example 1: Calculate the work required to increase the radius of a soap bubble from 2 cm to 4 cm. The surface tension of the soap solution is 0.03 N/m.
Solution: Surface energy (E) is given by:
\(\displaystyle E = \sigma \cdot A \)
For a soap bubble, there are two surfaces (inner and outer), so the total surface area is:
\(\displaystyle A = 2 \cdot 4\pi r^2 = 8\pi r^2 \)
Initial radius (r1) = 2 cm = 0.02 m
Final radius (r2) = 4 cm = 0.04 m
Initial surface area (A1):
\(\displaystyle A_1 = 8\pi (0.02)^2 = 8\pi \cdot 0.0004 = 0.0032\pi \, \text{m}^2 \)
Final surface area (A2):
\(\displaystyle A_2 = 8\pi (0.04)^2 = 8\pi \cdot 0.0016 = 0.0128\pi \, \text{m}^2 \)
Change in surface area (∆A):
\(\displaystyle \Delta A = A_2 – A_1 = 0.0128\pi – 0.0032\pi = 0.0096\pi \, \text{m}^2 \)
Work done (W) to increase the radius:
\(\displaystyle W = \sigma \cdot \Delta A = 0.03 \cdot 0.0096\pi \)
\(\displaystyle W = 0.000288\pi \, \text{J} \)
\(\displaystyle W \approx 0.000904 \, \text{J} \)
So, the work required to increase the radius is approximately (0.000904 J).
Example 2: Calculate the change in surface energy when a single water droplet of radius 1 mm splits into 1000 identical smaller droplets. The surface tension of water is 0.072 N/m.
Solution: Initial radius (r1) = 1 mm = 0.001 m; Number of smaller droplets (n) = 1000
Volume of one large droplet (V):
\(\displaystyle V = \frac{4}{3} \pi r_1^3 \)
Volume of one smaller droplet (Vs):
\(\displaystyle V_s = \frac{V}{n} = \frac{4}{3} \pi r_1^3 / 1000 \)
\(\displaystyle r_s = \left( \frac{r_1^3}{1000} \right)^{1/3} = \frac{r_1}{10} = 0.0001 \, \text{m} \)
Initial surface area (A1):
\(\displaystyle A_1 = 4 \pi r_1^2 = 4 \pi (0.001)^2 = 4 \pi \cdot 0.000001 = 0.000004\pi \, \text{m}^2 \)
The total surface area of smaller droplets (As):
\(\displaystyle A_s = n \cdot 4 \pi r_s^2 = 1000 \cdot 4 \pi (0.0001)^2 \)
\(\displaystyle A_s = 1000 \cdot 4 \pi \cdot 0.00000001 = 0.00004\pi \, \text{m}^2 \)
Change in surface area (∆A):
\(\displaystyle \Delta A = A_s – A_1 = 0.00004\pi – 0.000004\pi = 0.000036\pi \, \text{m}^2 \)
Change in surface energy (∆E):
\(\displaystyle \Delta E = \sigma \cdot \Delta A = 0.072 \cdot 0.000036\pi \)
\(\displaystyle \Delta E = 0.000002592\pi \, \text{J} \)
\(\displaystyle \Delta E \approx 0.00000814 \, \text{J} \)
So, the change in surface energy is approximately (0.00000814 J).
Example 3: Determine the height to which water will rise in a capillary tube of radius 0.5 mm if the surface tension of water is 0.072 N/m and the density of water is (1000 kg/m3). Assume the contact angle is zero.
Solution: The height (h) of capillary rise is given by:
\(\displaystyle h = \frac{2\sigma \cos \theta}{\rho g r} \)
Given:
- Surface tension (σ) = 0.072 N/m
- Density of water (ρ) = (1000 kg/m3)
- Radius of capillary (r) = 0.5 mm = (0.0005 m)
- Contact angle (θ) = 0 (so cos θ = 1))
- Acceleration due to gravity (g) = (9.8 m/s2)
Substituting the values:
\(\displaystyle h = \frac{2 \times 0.072 \times 1}{1000 \times 9.8 \times 0.0005} \)
\(\displaystyle h = \frac{0.144}{4.9 \times 10^{-1}} \)
\(\displaystyle h = \frac{0.144}{0.49} \)
\(\displaystyle h \approx 0.293 \, \text{m} \)
So, the height to which water will rise in the capillary tube is approximately 0.293 m or 29.3 cm.
Example 4: A liquid has a surface tension of 0.076 N/m at (20∘C) and 0.072 N/m at (40∘ C). Calculate the percentage decrease in surface tension due to the increase in temperature.
Solution: Initial surface tension (σ1) = 0.076 N/m
Final surface tension (σ2) = 0.072 N/m
Percentage decrease in surface tension (%∆σ):
\(\displaystyle \%\Delta \sigma = \frac{\sigma_1 – \sigma_2}{\sigma_1} \times 100 \)
Substituting the values:
\(\displaystyle \%\Delta \sigma = \frac{0.076 – 0.072}{0.076} \times 100 \)
\(\displaystyle \%\Delta \sigma = \frac{0.004}{0.076} \times 100 \)
\(\displaystyle \%\Delta \sigma \approx 5.26\% \)
So, the percentage decrease in surface tension due to the increase in temperature is approximately (5.26%).
Example 5: If a spherical droplet of water with a radius of 3 mm splits into 8 smaller droplets of equal size, calculate the new surface area created. Assume the surface tension of water is 0.072 N/m.
Solution: Initial radius (R) = 3 mm = 0.003 m; Number of smaller droplets (n) = 8
Volume of one large droplet (V):
\(\displaystyle V = \frac{4}{3} \pi R^3 \)
Volume of one smaller droplet (Vs):
\(\displaystyle V_s = \frac{V}{n} = \frac{4}{3} \pi R^3 / 8 \)
\(\displaystyle r_s = \left( \frac{R^3}{8} \right)^{1/3} = \frac{R}{2} = 0.0015 \, \text{m} \)
Initial surface area (A1):
\(\displaystyle A_1 = 4 \pi R^2 = 4 \pi (0.003)^2 = 4 \pi \cdot 0.000009 = 0.000036\pi \, \text{m}^2 \)
The total surface area of smaller droplets (As):
\(\displaystyle A_s = n \cdot 4 \pi r_s^2 = 8 \cdot 4 \pi (0.0015)^2 \)
\(\displaystyle A_s = 8 \cdot 4 \pi \cdot 0.00000225 = 0.000072\pi \, \text{m}^2 \)
The new surface area created:
\(\displaystyle \Delta A = A_s – A_1 = 0.000072\pi – 0.000036\)
\(\displaystyle pi = 0.000036\pi \, \text{m}^2 \)
So, the new surface area created is \(\displaystyle 0.000036\pi \, \text{m}^2\).
Example 6: A capillary tube of radius 0.1 mm is dipped vertically into a liquid of density 800 kg/m³. The liquid rises to a height of 6 cm in the tube. Calculate the surface tension of the liquid. Assume the contact angle is zero.
Solution: Height of rise (h) = 6 cm = 0.06 m
Radius of capillary (r) = 0.1 mm = (0.0001 m)
Density of liquid (ρ) = 800 kg/m³
Contact angle (θ) = 0 (so cos θ= 1))
Acceleration due to gravity (g) = (9.8 m/s2)
The height of capillary rise is given by:
\(\displaystyle h = \frac{2\sigma \cos \theta}{\rho g r} \)
Solving for (σ):
\(\displaystyle \sigma = \frac{h \rho g r}{2 \cos \theta} \)
\(\displaystyle \sigma = \frac{0.06 \times 800 \times 9.8 \times 0.0001}{2 \times 1} \)
\(\displaystyle \sigma = \frac{0.06 \times 800 \times 9.8 \times 0.0001}{2} \)
\(\displaystyle \sigma = \frac{0.04704}{2} \)
\(\displaystyle \sigma = 0.02352 \, \text{N/m} \)
So, the surface tension of the liquid is (0.02352 N/m).
FAQs
What is surface energy, and how is it defined in the context of physics?
Surface energy is the amount of energy required to increase the surface area of a liquid by a unit area. It is a measure of the cohesive forces acting at the surface of a liquid, which cause the surface to behave like a stretched elastic membrane. Surface energy is typically measured in joules per square meter (J/m²).
How does surface energy relate to surface tension in liquids?
Several factors affect the surface energy of a liquid, including temperature, the nature of the liquid (its molecular composition and intermolecular forces), and the presence of impurities or surfactants. Generally, surface energy decreases with increasing temperature, as thermal motion reduces the cohesive forces between molecules.
How is surface energy measured experimentally?
Surface energy can be measured using several methods, including the sessile drop method, where a drop of liquid is placed on a solid surface and the contact angle is measured; the Wilhelmy plate method, where a thin plate is dipped into the liquid and the force is measured; and the capillary rise method, where the height of liquid rise in a capillary tube is measured. Each method provides insights into the surface tension, which is directly related to surface energy.
Can you explain how surface energy influences the behavior of droplets on surfaces?
Surface energy influences the wetting behavior of droplets on surfaces. High surface energy surfaces tend to attract liquid molecules, causing droplets to spread out and form a low contact angle (good wetting). Low surface energy surfaces repel liquid molecules, causing droplets to bead up and form a high contact angle (poor wetting). This behavior is important in applications such as coatings, adhesives, and waterproof materials.
What role does surface energy play in phenomena like capillarity and adhesion?
Surface energy plays a crucial role in capillarity, where liquid rises or falls in a narrow tube due to the interaction between the liquid and the tube’s surface. High surface energy of the liquid and tube material enhances capillary action. In adhesion, surface energy determines how well two materials stick together. High surface energy materials typically adhere better because of stronger intermolecular forces at the interface.
How do surfactants affect the surface energy of liquids, and what are some practical applications of this effect?
Surfactants are substances that reduce the surface energy of liquids by concentrating at the surface and disrupting the cohesive forces between liquid molecules. This reduction in surface energy lowers surface tension, allowing liquids to spread more easily on surfaces. Practical applications of surfactants include detergents, which help water spread and penetrate fabrics for better cleaning, and emulsifiers, which stabilize mixtures of immiscible liquids like oil and water.
