Surface Tension

The concept of surface tension has fascinated scientists for centuries. The ancient Greeks first observed it, and one of the earliest recorded observations was by Hero of Alexandria, a Greek mathematician, and engineer, around 10 AD – 70 AD. He noticed the effects of surface tension in his experiments and inventions, such as the water clock, which utilized capillarity.

However, it wasn’t until the 18th century that the phenomenon began to be studied more scientifically. In 1751, Johann Andreas Segner, a German scientist, introduced the concept of surface tension of liquids and attempted to describe capillary action mathematically.

The term “surface tension” itself was coined in the 19th century by two prominent scientists: Thomas Young and Pierre-Simon Laplace. They were interested in understanding the forces that act on the surface of a liquid and developed the mathematical framework that described these forces.

Young and Laplace’s work laid the foundation for modern surface science, and their theories are still used today to explain various phenomena related to liquids. Their contributions helped to establish surface tension as a key concept in physics, particularly in fluid mechanics.

Through the years, the study of surface tension has evolved, and scientists have developed various methods to measure and understand this force. Despite its long history of scientific observation, the complexity of surface tension and its interactions at different interfaces is still a subject of ongoing research.

What is Surface Tension?

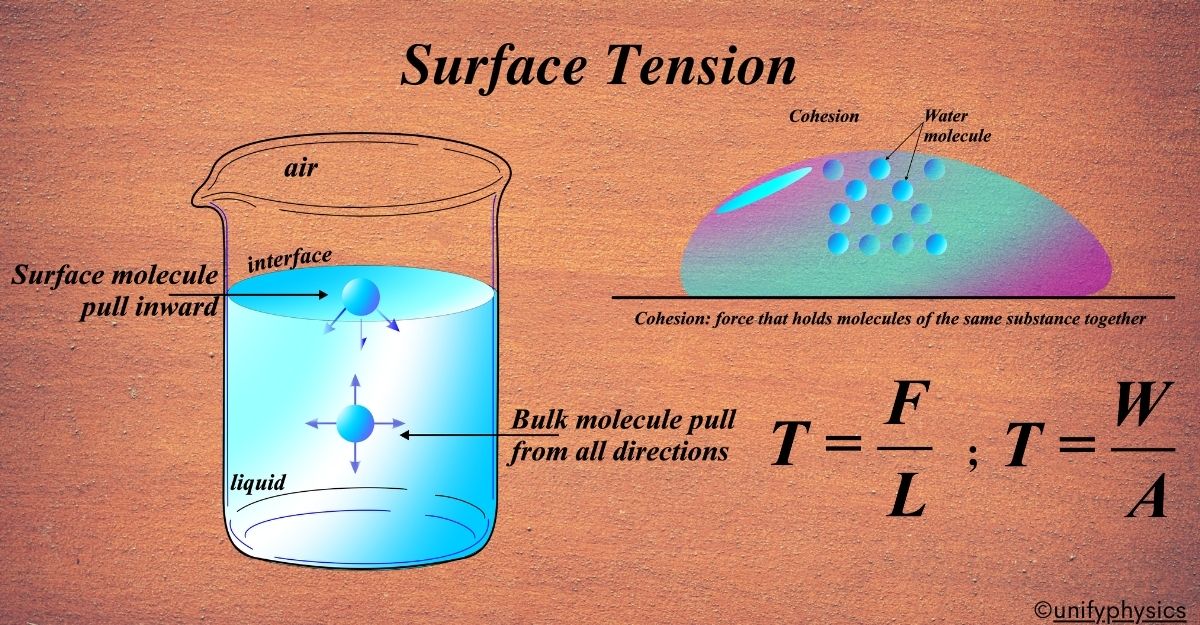
Surface tension (σ) is the force that acts on the surface of a liquid, causing it to behave as if it were covered with a stretched elastic membrane. This force arises because molecules at the surface of the liquid experience a net inward force due to the cohesive interactions with neighboring molecules. As a result, the surface tends to minimize its area, creating a high tension.

Imagine you’re trying to fill a glass with water, and you keep pouring until the water forms a dome above the rim without spilling over. This is possible because of a property of liquids called surface tension.

Surface tension is like an invisible skin on the surface of liquids. It’s the reason why raindrops are spherical, why you can float a needle on water if you place it gently, and why some insects can walk on water without sinking.

But what exactly is it? Well, surface tension is the result of the attraction between the molecules of a liquid. Molecules in the middle of the liquid are surrounded by other molecules and are pulled equally in all directions. However, molecules at the surface don’t have molecules above them, so they’re pulled more strongly toward the other molecules next to and below them. This creates a sort of ‘net’ that makes the surface under tension, just like a stretched elastic band.

This tension forces the liquid to take up the smallest possible surface area. For a drop of water, the smallest area is a sphere, which is why drops are usually round.

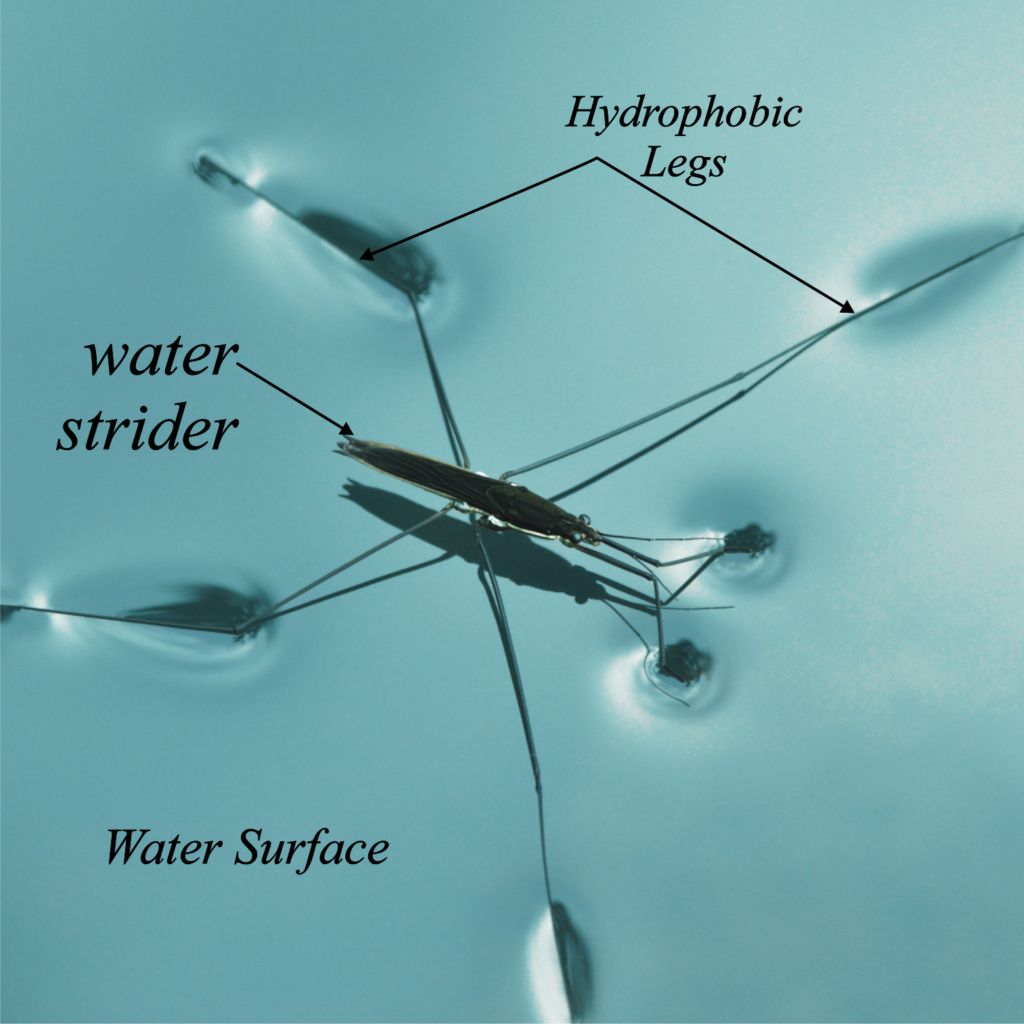
Certain spiders, such as water striders, can walk on the surface of water without sinking. This seemingly miraculous ability is due to surface tension. Let’s break down how this works:

The weight of the spider creates a downward force, but this force is counteracted by the surface tension of the water. As long as the spider’s weight is less than the force provided by the surface tension, it will not break through the surface. The spider moves carefully, causing minimal disturbance to the water’s surface, which helps it maintain its position without sinking.

How Surface Tension Supports the Spider

• Force Distribution: The spider’s legs spread out its weight over a larger area, which means the force exerted on any single point is minimal.
• Surface Film: The surface tension creates a supporting “film” that can hold the spider up.
• Hydrophobic Legs: The spider’s legs repel water, helping it stay on the surface and not get wet, which also aids in staying above water.

Formula, Unit, and Dimension of Surface Tension

Surface tension can be thought of as the strength of the surface of a liquid. To measure this strength, we use a formula that relates the force exerted by the surface tension to the length over which this force acts. The formula is:

\(\displaystyle T = \frac{F}{L} \)

Here,(T) stands for surface tension, (F) is the force exerted along the surface of the liquid, and (L) is the length of the line over which the force is acting. Imagine pulling a wire loop out of a soapy solution; the force you feel is the surface tension acting along the perimeter of the wire.

Unit of Surface Tension: The unit of surface tension in the International System of Units (SI) is Newton per meter (N/m). This unit tells us how much force is acting per unit length of the surface.

Dimension of Surface Tension: In physics, every physical quantity can be expressed in terms of basic dimensions. For surface tension, the dimensional formula is: [M¹ L⁰ T^-2]

This means surface tension is dimensionally represented as mass (M) to the power of 1, length (L) to the power of 0 (since it’s per meter, it cancels out), and time (T) to the power of -2.

Surface Tension at the Molecular Level

At the molecular level, surface tension is the result of the greater attraction that molecules on the surface experience from the molecules beneath them, compared to the air above. This imbalance of forces makes the surface act like a stretched elastic membrane.

When we talk about surface tension, we’re looking at the behavior of liquid molecules at the very surface compared to those inside the liquid. At the molecular level, surface tension is all about how the molecules interact with each other.

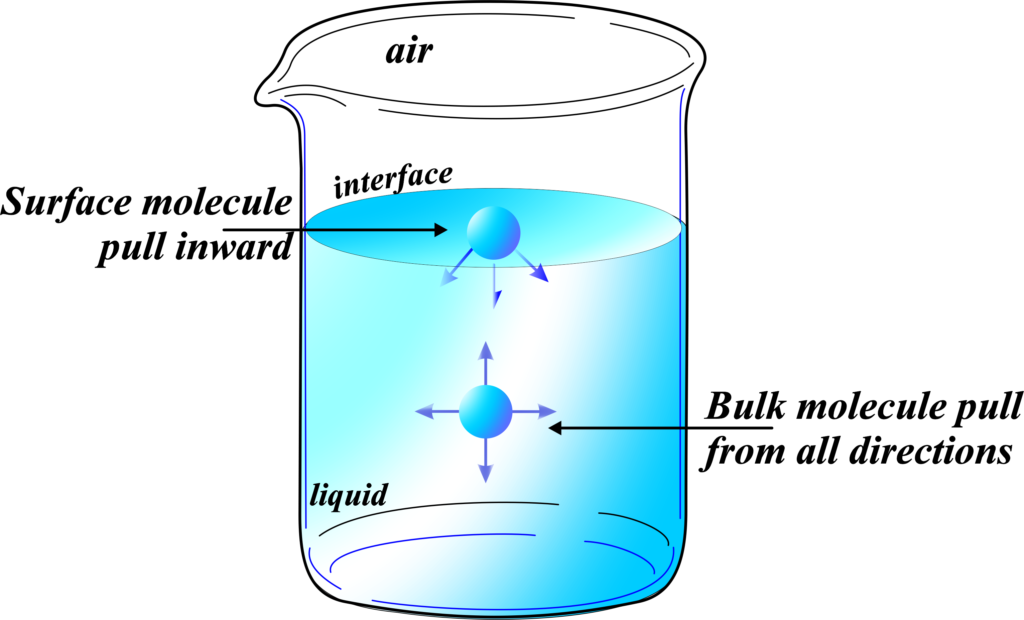
Inside a liquid, each molecule is surrounded by other molecules. These molecules are attracted to each other by forces known as intermolecular forces. Because they’re surrounded, the forces they experience from their neighbors are balanced out in all directions.

However, the molecules at the surface are a different story. They don’t have any liquid molecules above them, only air or maybe another liquid or solid. This means the forces on surface molecules are not balanced. They feel a stronger pull from the molecules below and beside them than from the air above. This imbalance causes the surface molecules to be pulled inward, towards the rest of the liquid.

This inward pull makes the surface of the liquid contract and behaves as if it’s covered by an invisible film. This is what we observe as surface tension. It’s like a stretched elastic sheet, trying to shrink into the smallest possible area. This is why drops of water tend to be round and why you can fill a glass slightly above the brim without the water spilling over.

At the molecular level, surface tension is the result of the cohesive forces between the molecules. Cohesive forces are the intermolecular forces that make molecules stick together. They are strongest at the surface where the molecules are pulled inward, creating tension.

What Causes Surface Tension?

Surface tension is caused by intermolecular forces such as Van der Waals forces, which draw the liquid particles together. Along the surface, particles are pulled toward the rest of the liquid, creating a state of tension.

Have you ever wondered why water beads up on a freshly waxed car or why some insects can skim across a pond without sinking? The answer lies in a fascinating property of liquids called surface tension.

Surface tension is caused by the cohesive forces between liquid molecules. These are the forces that make molecules stick together. Now, imagine each water molecule as a tiny magnet. Inside the liquid, each molecule is pulled equally in all directions by its neighboring molecules. But at the surface, there are no water molecules above, so the ‘magnets’ only pull sideways and downwards.

This imbalance creates a sort of ‘skin’ on the liquid’s surface, which is strong enough to hold up light objects and even some small creatures. This ‘skin’ is what we call surface tension.

So, when you see a drop of water holding its shape or an insect walking on water, it’s the surface tension at work, created by the invisible ‘magnetic’ forces between the molecules pulling together to minimize the surface area and create that tension.

Van der Waals force:

At a molecular level, the main force behind this is the Van der Waals force, which is a type of attraction between molecules. It’s not as strong as the bond that holds molecules together in a solid, but it’s powerful enough to make the surface of a liquid act like a stretched elastic membrane.

When we talk about surface tension, we’re talking about the ‘stickiness’ of the surface of a liquid. This ‘stickiness’ is due to a type of force called the Van der Waals force.

Imagine each molecule in a liquid as a tiny ball that can stick to other balls around it. The Van der Waals force is like the invisible ‘glue’ that holds these balls together. It’s not as strong as the glue that holds the molecules in a solid, but it’s just enough to give liquids a surface that can resist some force.

Now, the Van der Waals force is a combination of three different forces:

• London Dispersion Forces: These are like temporary ‘magnets’ created when the electrons in a molecule crowd to one side, making one side slightly negative and the other slightly positive.
• Dipole-Dipole Interactions: These happen between molecules that are permanent ‘magnets’ (they have a positive side and a negative side) and they line up so that opposite charges attract.
• Hydrogen Bonds: These are special dipole-dipole interactions that happen when hydrogen is involved, and they’re particularly strong ‘magnets’.

In the context of surface tension, these forces work at the surface of a liquid to pull the molecules toward each other and towards the interior of the liquid. This creates a sort of ‘film’ on the surface that’s under tension – hence the name surface tension.

So, when you see water forming droplets on a leaf or filling up a glass just above the rim without spilling, it’s the Van der Waals force in action, creating surface tension and allowing the liquid to maintain its shape against gravity and other forces.

Cohesion and Surface Tension:

Cohesion refers to the attractive force between molecules of the same substance. In liquids, this cohesive force pulls the molecules at the surface inward, leading to surface tension.

When we talk about surface tension, we’re talking about the ‘stickiness’ at the surface of liquids. This ‘stickiness’ is due to a property called cohesion.

Cohesion is the force that holds molecules of the same substance together. Think of it like a team of people holding hands. The stronger they hold hands, the less likely they are to let go when pulled. In a liquid, molecules ‘hold hands’ with their neighbors through forces called intermolecular forces.

Now, at the surface of a liquid, the molecules don’t have neighbors above them, so they hold on even tighter to the ones next to and below them. This creates a sort of ‘skin’ on the liquid’s surface, which is strong enough to hold up light objects and even some small creatures. This ‘skin’ is what we call surface tension.

So, cohesion is the ‘holding hands’ part, and surface tension is the ‘skin’ that forms because of that. It’s like when you stretch a rubber band; the tension you feel is similar to the surface tension created by cohesive forces in a liquid.

At the molecular level, molecules on the surface are pulled inward by cohesive forces, reducing the surface area. Molecules inside the liquid experience zero net force, since they have neighbors on all sides.

This concept is important because it explains why drops of water are round, why soap helps clean dishes, and why water can climb up a thin tube against gravity—a process called capillary action.

Factors Affecting Surface Tension

Surface tension isn’t always the same; it can change based on different conditions. Here are some key factors that can affect it:

• Temperature: Just like a rubber band becomes looser when heated, surface tension decreases as the temperature goes up. This happens because the molecules move faster and aren’t as close together, reducing the ‘stickiness’ between them. At a certain high temperature, called the critical temperature, surface tension becomes zero because the liquid turns into a gas.
• Impurities: Adding different substances to a liquid can change its surface tension. For example, salt can make the surface tension of water go up because it changes how water molecules stick to each other. On the other hand, soap can reduce surface tension, which is why it helps clean things by making water spread out more easily.
• Nature of the Liquid: Different liquids have different surface tensions. Water has a higher surface tension compared to alcohol because the forces between water molecules are stronger.
• Presence of Surfactants: Surfactants are special substances that can greatly reduce surface tension. They do this by getting in between the liquid’s molecules and pushing them apart. Detergents and soaps contain surfactants, which is why they can break up grease and dirt so well.
• Oxidation: When a liquid is exposed to air, it can undergo oxidation, which can affect its surface tension. For instance, oxygen from the air can decrease the surface tension of certain substances.

These factors is important because they can influence how a liquid behaves in different situations. For example, knowing about surfactants can help explain why some insects can walk on water: they release substances that lower the water’s surface tension right under their feet.

Methods of Measurement of Surface Tension

Surface tension is a key property of liquids, and measuring it helps us understand how liquids behave. There are several methods to measure surface tension, each with its unique approach:

• Capillary Rise Method: This method uses the rise of a liquid in a thin tube, or capillary, to measure surface tension. When a capillary tube is placed in a liquid, the liquid will rise in the tube due to surface tension. The height to which the liquid rises is related to its surface tension.
• Wilhelmy Plate Method: In this method, a thin, vertical plate is dipped into the liquid, and the force required to pull it out is measured. This force is directly related to the surface tension of the liquid.
• Du Noüy Ring Method: Similar to the Wilhelmy plate, this method uses a ring instead of a plate. The ring is submerged in the liquid, and the force required to lift it from the liquid’s surface is measured to determine the surface tension.
• Drop Weight Method: Here, the weight of a drop that detaches from a dropper is used to calculate the surface tension. The larger the surface tension, the heavier the drop that can be suspended before it falls.
• Pendant Drop Method: A drop is suspended from a needle, and its shape is analyzed to determine the surface tension. The drop’s shape changes based on the surface tension of the liquid.
• Bubble Pressure Method: This method measures the pressure needed to blow a bubble in the liquid. The pressure at which a bubble is formed is related to the surface tension.
• Sessile Drop Method: A drop is placed on a solid surface, and its shape is analyzed. The contact angle that the drop makes with the surface can be used to calculate the surface tension.
• Spinning Drop Method: A drop of liquid is placed inside another liquid with a different density. When the system is spun, the drop stretches and the surface tension can be calculated based on the drop’s shape.
• Stalagmometric Method: This method involves counting the number of drops that fall from a liquid dropper in a given time. The size and weight of the drops are related to the surface tension.

These methods allow scientists and engineers to measure surface tension in various scenarios, from simple classroom experiments to complex industrial processes.

Given below in a table is the surface tension of various liquids:

Liquid	Surface Tension (N/m)
Water	0.07275
Mercury	0.485
Ethanol	0.02239
Glycerol	0.06340
Acetone	0.02397
Diethyl Ether	0.01710
Olive Oil	0.0328
Hexane	0.01840
Silicone Oil	0.021
Carbon Tetrachloride	0.02704

These values are typically measured at room temperature (around 20°C or 68°F) and can vary with temperature, impurities, and other factors. Observing the table of surface tension values for various liquids, we can make the following points:

• Water has a relatively high surface tension of 0.07275 N/m, which is why it forms droplets and can sustain small objects on its surface due to the cohesive forces between water molecules.
• Mercury stands out with the highest surface tension value of 0.485 N/m in the table, significantly higher than the other liquids, which is characteristic of its dense and cohesive nature.
• Ethanol and Acetone have much lower surface tension values (0.02239 N/m and 0.02397 N/m, respectively), indicating that they spread more easily on surfaces and evaporate faster than water.
• Glycerol has a surface tension value (0.06340 N/m) closer to water, reflecting its more viscous and sticky nature.
• Olive Oil and Hexane show lower surface tension values (0.0328 N/m and 0.01840 N/m, respectively), which explains their ability to spread thinly over surfaces.
• Silicone Oil and Carbon Tetrachloride have surface tensions lower than water but higher than most organic solvents listed, which may influence their behavior in mixtures and applications.

These observations help us understand the relative ‘stickiness’ or ‘stretchiness’ of the liquid surfaces, which is crucial for applications ranging from industrial processes to biological systems.

Also Read: Surface Energy

What is Angle of Contact?

The angle of contact is the angle at which a liquid interface meets a solid surface. It quantifies the wettability of a solid by the liquid.

Imagine you have a small droplet of water resting on a flat surface, like a leaf or a table. If you look closely at the point where the edge of the water droplet touches the surface, you’ll notice that it’s not just sitting flat; it makes a curve. This curve forms an angle with the surface, and that’s what we call the Angle of Contact.

The angle of Contact is the angle formed where the liquid surface meets the solid surface. To be more precise, it’s the angle between the tangent to the liquid surface at the point of contact and the solid surface itself, measured inside the liquid.

Here’s how you can visualize it:

1. Place a drop of water on a clean glass slide.
2. Look at the drop from the side to see the curve where the water meets the glass.
3. The angle formed by the curve of the water and the glass is the Angle of Contact.

This angle tells us a lot about how the liquid interacts with the solid. If the angle is less than 90 degrees, the liquid spreads out over the surface, which means it wets the surface well. This is called a wetting liquid. If the angle is more than 90 degrees, the liquid doesn’t spread out much and forms a droplet instead. This is called a non-wetting liquid.

The Angle of Contact depends on three things:

• The nature of the liquid (like water or oil)
• The solid surface it’s on (like glass or plastic)
• The surrounding environment (like air or another liquid)

It’s an important concept because it helps us understand and predict how liquids will behave on different surfaces, which is super useful in things like painting, printing, and even in nature, like how water beads up on a leaf.

Applications of Surface Tension

Surface tension is not just a concept in physics books; it’s a phenomenon that we encounter in our daily lives and various industries. Here are some fascinating applications:

• Water Striders: Ever seen insects that seem to skate across the surface of a pond? They can do this because their legs distribute their weight in such a way that they don’t break the surface tension of the water.
• Needles Floating on Water: With careful placement, a needle can be made to float on water. This is because the surface tension of water supports the needle’s weight without letting it sink.
• Detergents and Soaps: These everyday items reduce the surface tension of water, making it easier for the water to spread and clean surfaces by breaking down grease and dirt.
• Antiseptics: Products like Dettol have a low surface tension, which allows them to spread quickly over a surface, providing better coverage when disinfecting.
• Capillary Action: This is the ability of a liquid to flow in narrow spaces without the assistance of external forces. It’s why plants can draw water from their roots up to their leaves and why a paper towel absorbs spills.
• Medical Applications: Surface tension is crucial in the formation of droplets, which is important in medical diagnostics. It’s used in the design of assays and lab-on-a-chip devices that can perform multiple laboratory functions on a single chip.
• Inkjet Printing: Printers use surface tension to control the droplets of ink. The ink must have the right surface tension to form perfect droplets that create clear, crisp images and text.
• Food Industry: Surface tension plays a role in the characterization of products like oils, emulsions, and foams, which are essential in food processing and quality control.
• Bubble Formation: Bubbles and foams in drinks like beer and cappuccinos are all about surface tension. It’s also why you can blow bubbles with soapy water.
• Paints and Coatings: The surface tension of paints is adjusted to ensure they spread evenly over a surface and provide a smooth finish.

These examples show how surface tension is not just a theoretical concept but a practical one that affects many aspects of our lives and technology.

Solved Examples

Example 1: A glass capillary tube with a radius of 0.2 mm is vertically dipped in water. If the surface tension of water is 0.072 N/m and the contact angle is zero, calculate the height to which water rises in the tube. The density of water is (1000 kg/m³).

Solution: The height (h) of capillary rise is given by:

\(\displaystyle h = \frac{2\sigma \cos \theta}{\rho g r} \)

Given:

• Surface tension (σ) = 0.072 N/m
• Contact angle (θ) = 0 (so; cosθ = 1))
• Density of water (ρ) = (1000 kg/m³)
• Radius of capillary (r) = 0.2 mm = 0.0002 m
• Acceleration due to gravity (g) = (9.8 m/s²)

Substituting the values:

\(\displaystyle h = \frac{2 \times 0.072 \times 1}{1000 \times 9.8 \times 0.0002} \)
\(\displaystyle h = \frac{0.144}{1.96} \)
\(\displaystyle h \approx 0.0735 \, \text{m} \)

So, the height to which water rises in the tube is approximately (0.0735 m) or 7.35 cm.

Example 2: A spherical water droplet has a radius of 1 mm. Calculate the excess pressure inside the droplet if the surface tension of water is 0.072 N/m.

Solution: The excess pressure (∆ P) inside a spherical droplet is given by:

\(\displaystyle \Delta P = \frac{2\sigma}{r} \)

Given: Surface tension (σ) = 0.072 N/m; Radius (r) = 1 mm = 0.001 m

Substituting the values:

\(\displaystyle \Delta P = \frac{2 \times 0.072}{0.001} \)
\(\displaystyle \Delta P = \frac{0.144}{0.001} \)
\(\displaystyle \Delta P = 144 \, \text{Pa} \)

So, the excess pressure inside the droplet is (144 Pa).

Example 3: Calculate the work done in blowing a soap bubble from a radius of 2 cm to 4 cm. The surface tension of the soap solution is 0.03 N/m.

Solution: The surface energy (E) of a soap bubble (with two surfaces) is given by:

\(\displaystyle E = \sigma \cdot 2 \cdot 4\pi r^2 = 8\pi \sigma r^2 \)

Initial radius (r₁) = 2 cm = 0.02 m ; Final radius (r₂) = 4 cm = 0.04 m

Initial surface energy (E₁):

\(\displaystyle E_1 = 8\pi \times 0.03 \times (0.02)^2 \)
\(\displaystyle E_1 = 8\pi \times 0.03 \times 0.0004 \)
\(\displaystyle E_1 = 0.0096\pi \, \text{J} \)

Final surface energy (E₂):

\(\displaystyle E_2 = 8\pi \times 0.03 \times (0.04)^2 \)
\(\displaystyle E_2 = 8\pi \times 0.03 \times 0.0016 \)
\(\displaystyle E_2 = 0.0384\pi \, \text{J} \)

Change in surface energy (∆ E):

\(\displaystyle \Delta E = E_2 – E_1 = 0.0384\pi – 0.0096\pi \)
\(\displaystyle \Delta E = 0.0288\pi \, \text{J} \)
\(\displaystyle \Delta E \approx 0.0905 \, \text{J} \)

So, the work done in blowing the soap bubble is approximately (0.0905 J}.

Example 4: Compare the capillary rise of water and mercury in a capillary tube of radius 0.1 mm. The surface tension of water is 0.072 N/m with a contact angle of (0^∘), and for mercury, the surface tension is 0.465 N/m with a contact angle of (140^∘). The densities are (1000 kg/m³) for water and (13500 kg/m³) for mercury.

Solution: Height (h) of capillary rise is given by:

\(\displaystyle h = \frac{2\sigma \cos \theta}{\rho g r} \)

For water:

\(\displaystyle \sigma = 0.072 \, \text{N/m}, \)
\(\displaystyle \theta = 0^\circ \, (\cos 0^\circ = 1), \)
\(\displaystyle \rho = 1000 \, \text{kg/m}^3, \)
\(\displaystyle r = 0.1 \, \text{mm} = 0.0001 \, \text{m}, \)
\(\displaystyle g = 9.8 \, \text{m/s}^2 \)

\(\displaystyle h_{\text{water}} = \frac{2 \times 0.072 \times 1}{1000 \times 9.8 \times 0.0001} \)
\(\displaystyle h_{\text{water}} = \frac{0.144}{0.98} \)
\(\displaystyle h_{\text{water}} \approx 0.147 \, \text{m} \)

For mercury:

\(\displaystyle \sigma = 0.465 \, \text{N/m}, \)
\(\displaystyle \theta = 140^\circ \, (\cos 140^\circ = -\cos 40^\circ = -0.766), \)
\(\displaystyle \rho = 13500 \, \text{kg/m}^3, \)
\(\displaystyle r = 0.1 \, \text{mm} = 0.0001 \, \text{m}, \)
\(\displaystyle g = 9.8 \, \text{m/s}^2 \)

\(\displaystyle h_{\text{mercury}} = \frac{2 \times 0.465 \times (-0.766)}{13500 \times 9.8 \times 0.0001} \)
\(\displaystyle h_{\text{mercury}} = \frac{-0.7113}{1.323} \)
\(\displaystyle h_{\text{mercury}} \approx -0.538 \, \text{m} \)

The negative sign indicates a depression rather than a rise. So, the capillary rise of water is approximately (0.147 m) (14.7 cm), and mercury shows a depression of approximately (0.538 m) (53.8 cm).

Example 5: Calculate the surface energy required to form a liquid film of area (0.1 m²) if the surface tension of the liquid is 0.05 N/m.

Solution: Surface energy (E) is given by:
[ E = \sigma \cdot A ]

Given: Surface tension (σ) = 0.05 N/m; Area (A) = 0.1 m²

\(\displaystyle E = 0.05 \times 0.1 \)
\(\displaystyle E = 0.005 \, \text{J} \)

So, the surface energy required to form the liquid film is (0.005 J).

FAQs