The story of Earth’s magnetic field is as old as the planet itself. It’s a tale of discovery, mystery, and scientific breakthroughs. Long before the term “magnetic field” was coined, ancient navigators used lodestones, naturally magnetized pieces of the mineral magnetite, to navigate the seas. The Chinese were among the first to notice that these stones always pointed in the same direction when suspended freely, leading to the creation of the first compasses.
The first scientific measurement of Earth’s magnetic field occurred in the 16th century. In 1544, George Hartmann measured the vertical component of the field. This was a significant step forward because it showed that the Earth’s magnetic field had a direction and strength that could be quantified.
Fast forward to the 19th century, when Carl Friedrich Gauss developed a way to measure the intensity of the magnetic field in 1833. He also proposed that the field could be due to electric currents in the Earth’s interior.
One of the most intriguing aspects of Earth’s magnetic field is its ability to reverse. Studies of the ocean floor and volcanic rocks have shown that the magnetic poles have switched places multiple times throughout Earth’s history. These geomagnetic reversals have occurred at irregular intervals, averaging several hundred thousand years apart.
Today, we understand that Earth’s magnetic field is generated by the dynamo effect in the outer core. The movement of molten iron and nickel generates electric currents, which in turn create the magnetic field. This theory was solidified in the 20th century as scientists developed a better understanding of the Earth’s interior.
What Is Earth’s Magnetic Field?
Earth’s magnetic field, also known as the geomagnetic field, is an invisible force field that extends from the Earth’s interior into space. It protects our planet from solar winds and cosmic rays.
Imagine a giant bar magnet placed at the center of the Earth, tilted slightly from the north-south axis. This is what Earth’s magnetic field is like. It’s an invisible force that extends from the Earth’s interior out into space, creating a protective shield known as the magnetosphere.
Earth’s magnetic field acts like a protective blanket. It shields us from the solar wind, which is a stream of charged particles emitted by the Sun. Without this magnetic field, these particles could strip away the ozone layer that protects us from harmful ultraviolet radiation.
The geomagnetic field is primarily dipolar, meaning it has two main poles, much like a regular bar magnet. These are the geomagnetic North and South poles. However, unlike a simple bar magnet, the Earth’s magnetic field gets distorted as it goes away from the surface due to various influences like the solar wind and the conditions of space.
This field extends several tens of thousands of kilometers into space, forming the magnetosphere. This region is where the Earth’s magnetic field interacts with solar and cosmic particles, deflecting them and thus playing a crucial role in maintaining our atmosphere and protecting life on Earth.
An interesting fact about Earth’s magnetic poles is that they are not fixed. They wander over time. The North Magnetic Pole, for example, is currently found in Northern Canada and is slowly moving. This movement is normal and part of the dynamic nature of the Earth’s magnetic field.
If we could see the magnetic field lines, they would travel in closed, continuous loops, emerging near the magnetic poles. Near the poles, these lines are nearly vertical, and as we move away from the poles, they become more horizontal.
When we use a compass, its needle aligns with these invisible magnetic field lines, pointing toward the Magnetic North Pole. However, this is not the same as the Geographic North Pole, which is a fixed location defined by Earth’s rotational axis.
So, Earth’s magnetic field is a dynamic and complex force that not only guides compasses but also protects our planet from the harsh environment of space. It’s a fundamental part of Earth’s natural defense system, making life possible as we know it.
Theory of Earth’s Magnetism
The Dynamo Effect
At the heart of Earth’s magnetism is the Dynamo Effect. Imagine the Earth’s core as a bustling kitchen where the convection currents of molten iron and nickel are like boiling soup. These currents move because of the heat escaping from the core, and as they do, they carry charged particles with them.
These moving charges are like tiny electric currents, and when electric currents move, they create a magnetic field. This is the same principle that makes electromagnets work in science labs. So, the Earth’s core is like a natural dynamo – a generator of magnetic fields.
At the center of our planet lies the core, which is split into two parts: the solid inner core and the liquid outer core. The outer core is composed of molten iron and nickel, and it’s always on the move due to the heat escaping from the inner core.
As the Earth rotates, the liquid metal in the outer core moves around. This movement is essential because it carries electric charges with it. When electric charges move, they create a magnetic field—this is the basic principle behind any electric generator, and the Earth’s core is no different. It’s a natural dynamo.
For the Dynamo Effect to work, you need three ingredients:
- Conducting Fluid: The molten iron in the outer core is an excellent conductor of electricity.
- Rotation: The Earth’s rotation provides the necessary twist, organizing the flow of the molten metal.
- Energy Source: The heat from the inner core keeps the metal liquid and moving.
The Dynamo Effect is self-sustaining. The movement of the molten metal generates a magnetic field, which in turn induces more electric currents in the fluid. These currents then reinforce the magnetic field, and the cycle continues.
If we could see the Earth’s magnetic field, it would look like a series of lines looping from one pole to the other. Near the poles, these lines are nearly vertical, and they become more horizontal as you move towards the equator.
Convection currents in the outer core, driven by heat from the inner core, are what keep this dynamo going. These currents are like the conveyor belts that transport the electric charges and maintain the magnetic field over astronomical timescales.
Thanks to the Dynamo Effect, Earth has a magnetic field that extends far into space, forming the magnetosphere. This field protects us from solar winds and cosmic radiation, making life on Earth possible. The ionosphere, a layer of Earth’s atmosphere, becomes ionized due to solar radiation and contributes to Earth’s magnetism.
Ionization in the Atmosphere
High above the Earth’s surface, starting at about 50 km and extending up to several hundred kilometers, lies a layer of the atmosphere known as the ionosphere. This region is special because it’s filled with ions and free electrons, created by the action of solar radiation on the atoms and molecules of air.
The Sun is constantly emitting a stream of ultraviolet rays and other forms of radiation. When these rays hit the upper atmosphere, they have enough energy to knock electrons off the atoms and molecules they encounter. This process is called ionization.
The ionosphere is ionized by solar radiation, and it plays a crucial role in atmospheric electricity. It forms the inner edge of the magnetosphere, the area where Earth’s magnetic field interacts with solar and cosmic particles.
In the ionosphere, ions and electrons are free to move. They’re influenced by Earth’s magnetic field, which guides their motion. This interaction between charged particles and the magnetic field contributes to the overall magnetism of our planet.
The intensity of ionization in the atmosphere changes with the time of day and the seasons. During the day, the Sun’s rays are more direct, leading to higher levels of ionization. This daily variation affects the current in the ionosphere, which in turn influences the Earth’s magnetic field.
The ionosphere is not just a scientific curiosity; it has practical implications. It affects radio propagation, allowing radio waves to travel over long distances by bouncing off the ionized layers. It also impacts GPS signals that pass through this layer, making it a critical factor in modern communication and navigation systems.
So, the ionization of the atmosphere is a key piece in the puzzle of Earth’s magnetism. It’s a dynamic process, influenced by the Sun, that plays a significant role in shaping the magnetic environment of our planet.
What Causes Earth’s Magnetism?
The primary cause is the dynamo effect in the Earth’s outer core, where convection currents of molten iron generate magnetic fields. Imagine the Earth as a giant electric motor. At the center of this motor is the Earth’s core, which is made up of two parts: a solid inner core and a liquid outer core. The outer core is filled with molten iron and nickel, and it’s always on the move.
The movement of this molten metal is key to generating Earth’s magnetic field. As the Earth rotates, the liquid metal in the outer core swirls and flows. This flow of conductive material generates electric currents. These currents, in turn, create a magnetic field around the planet. This process is known as the geodynamo.
The heat escaping from the inner core is what keeps the metal in the outer core molten and moving. It’s like the fuel that powers the geodynamo. Without this heat, the motion would stop, and so would the generation of the magnetic field.
This magnetic field created by the geodynamo extends far out into space and forms what we call the magnetosphere. The magnetosphere acts like an invisible shield, protecting us from solar winds and cosmic rays that could strip away our atmosphere, including the ozone layer that keeps us safe from harmful ultraviolet radiation.
The beauty of the geodynamo is that it’s a self-sustaining process. The magnetic field it creates also helps to induce more electric currents in the outer core, which then strengthens the magnetic field even more. It’s a continuous cycle that has been going on for billions of years.
In simple terms, Earth’s magnetism is caused by the dynamo effect in the outer core. The heat-driven movement of molten iron generates electric currents, which in turn create the magnetic field that envelops our planet. It’s a fascinating natural phenomenon that not only makes compasses work but also keeps life on Earth safe from space’s dangers.
Components of Earth’s Magnetic Field
(i) Magnetic Inclination: The angle at which the magnetic field lines intersect the Earth’s surface.
Magnetic inclination, also known as dip angle or magnetic dip, is the angle between the Earth’s magnetic field lines and the horizontal plane at any given location.
It tells us how steeply the magnetic field lines dive into the Earth or emerge out of it. Magnetic inclination is a measure of how the Earth’s magnetic field interacts with the planet’s surface.
Imagine you’re holding a compass not flat in your hand, but vertically. In certain places on Earth, the compass needle won’t stay horizontal; instead, it will tilt up or down. This tilt is what we call the magnetic inclination. Near the equator, the inclination is close to zero, meaning the field lines are almost horizontal. At the equator, there’s a special line called the aclinic line, where the dip is zero degrees. Here, the magnetic field lines are parallel to the Earth’s surface. But as you move towards the poles, the inclination increases, and the field lines become more vertical.
The Earth’s magnetic field isn’t uniform; it changes depending on where you are. At the magnetic equator, the inclination is zero — the field lines run parallel to the Earth’s surface. But as you move towards the poles, the field lines curve and enter the Earth at steeper angles, increasing the inclination.
- Positive Inclination: When the north end of the compass needle tilts downwards (Northern Hemisphere).
- Negative Inclination: When the north end tilts upwards (Southern Hemisphere).
The magnetic inclination is represented by the letter I. The formula to calculate it is:
\(\displaystyle I = \tan^{-1}\left(\frac{Z}{H}\right) \)
- Z is the intensity of the magnetic field in the vertical direction.
- H is the intensity of the magnetic field in the horizontal direction.
This formula helps us understand the three-dimensional nature of the Earth’s magnetic field. It’s crucial for navigation, geophysics, and understanding how the Earth interacts with cosmic forces. At the magnetic equator, θ is 90 degrees, so I is 0, meaning the field lines are horizontal. As we move towards the poles, θ decreases, and I increase, indicating that the field lines become more vertical.
In 1544, George Hartmann first discovered the dip angle, and later in 1581, Robert Norman developed the dip circle, an instrument to measure the magnetic inclination. Now scientists use an instrument called a dip circle to measure magnetic inclination. It’s like a compass, but instead of a flat base, it has a circular one that allows the needle to pivot vertically. By observing the angle at which the needle settles, scientists can determine the magnetic inclination at that location.
Understanding magnetic inclination is crucial for navigation and for studying the Earth’s magnetic field. It helps in correcting compass readings for accurate navigation and also provides insights into the structure of the Earth’s interior and the geodynamo process that generates the magnetic field.
(ii) Magnetic Declination: The angle between magnetic north and true north at a particular location.
Magnetic declination, sometimes called magnetic variation, is the angle between magnetic north and true north at a particular location on Earth’s surface. It’s an essential concept for navigation because it helps correct compass readings to point to true north.
The Earth’s magnetic north, where a compass needle points, is not the same as the geographic north pole.
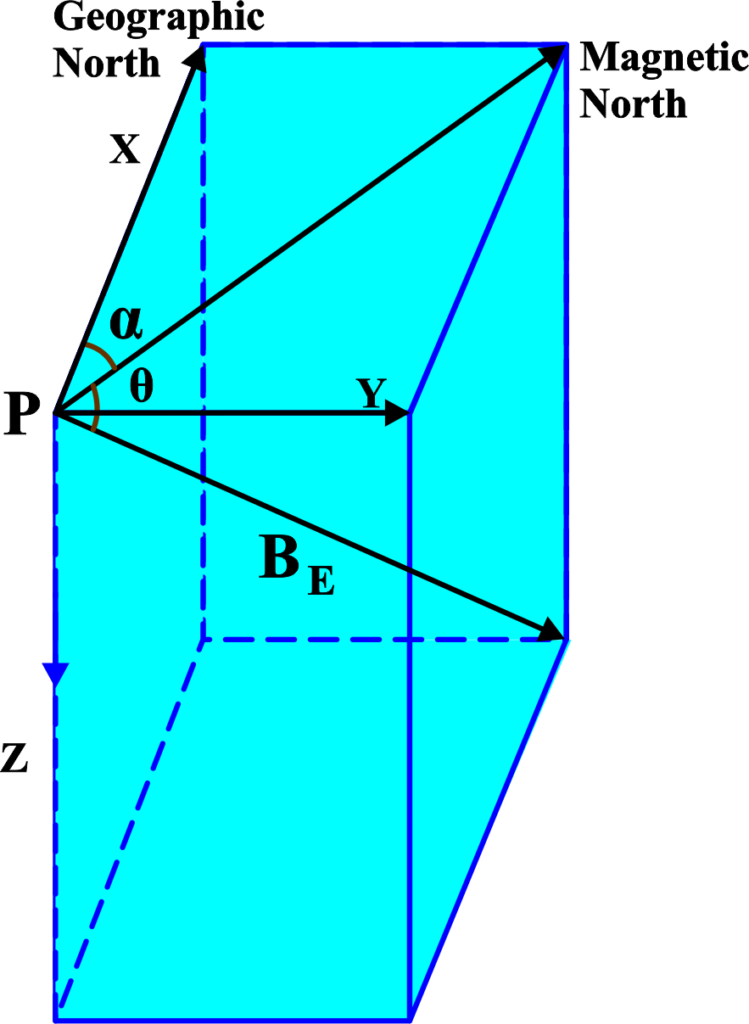
The magnetic north is located in northern Canada, not at the geographic North Pole. This misalignment is what we call magnetic declination.
Magnetic declination is measured as an angle. It can be positive or negative:
- Positive Declination: When magnetic north is east of true north.
- Negative Declination: When magnetic north is west of true north.
When navigating with a compass, if you don’t account for magnetic declination, you could end up off course. For example, if you’re trying to head straight north according to your compass, but the declination at your location is 10 degrees east, you’ll need to adjust your path 10 degrees west to find true north.
Isogonic lines connect points on the Earth’s surface that share a constant declination value. Agonic lines are those in which the declination value is zero.
The equation for magnetic declination is given by:
\(\displaystyle D = \tan^{-1}\left(\frac{Y}{X}\right) \)
X and Y are components of the Earth’s magnetic field in the north and east directions, respectively.
Magnetic declination isn’t the same everywhere and it changes over time due to the shifting of the Earth’s magnetic field. This means navigators need up-to-date information about the declination for their specific location. Magnetic declination varies depending on both location and time due to several factors:
- Geological Variations: Areas with higher concentrations of iron ore can affect local magnetic fields.
- Temporal Changes: The Earth’s magnetic field changes over time, which can alter declination values. For instance, the UK experienced a shift from a one-degree westerly declination in 2014 to zero degrees by 2020.
- Secular Change: It’s estimated that magnetic declination changes by about 20 to 2.5 degrees every hundred years.
Think of the Earth with two sets of north-south lines: one for geographic poles and one for magnetic poles. The angle where these two sets of lines intersect at your location is the magnetic declination.
(iii) Horizontal Component (H): The part of the magnetic field that runs parallel to the Earth’s surface.
The Earth’s magnetic field can be thought of as having different components based on direction. One of these is the horizontal component, denoted as H. It represents the part of the magnetic field that runs parallel to the Earth’s surface.
If you were to use a compass, the needle aligns with the Earth’s magnetic field. The compass needle lies in the horizontal plane and points towards the magnetic north. This direction, parallel to the ground, is the direction of the horizontal component H.
To measure H, scientists use instruments like magnetometers that can isolate this component from the total magnetic field. The strength of H varies depending on your location on Earth. Near the equator, H is stronger because the field lines are more horizontal. As you move towards the poles, H decreases because the field lines dip more into the Earth.
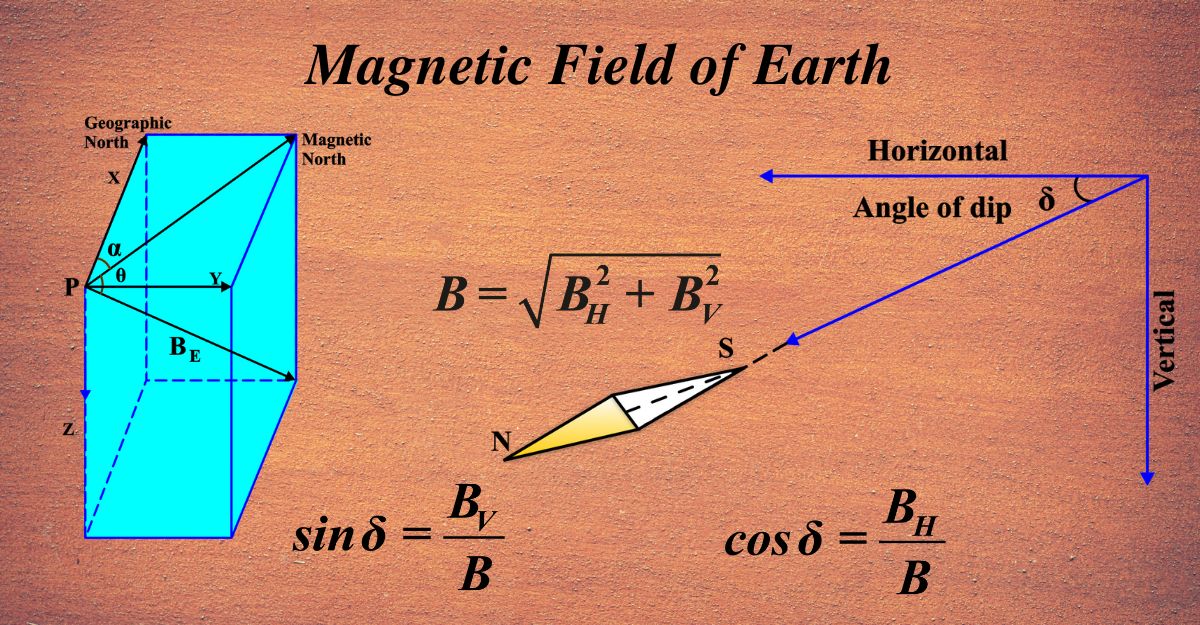
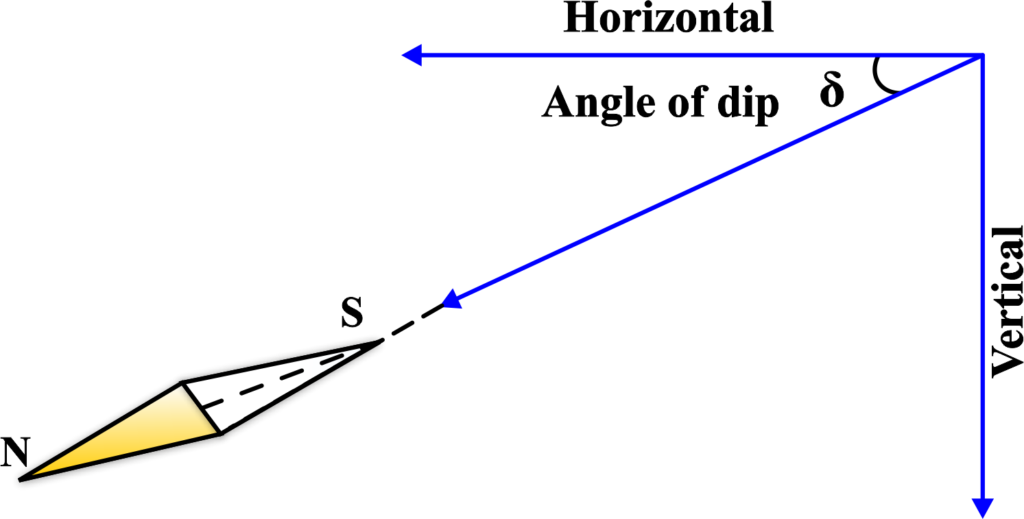
The strength of the horizontal component can be calculated using the total magnetic field strength (B) and the angle of dip (δ). The formula is:
\(\displaystyle B_H = B \cos \delta \)
- B is the total magnetic field strength.
- δ is the angle of dip, which is the angle between the total magnetic field and the horizontal plane.
The cosine function is used because it relates the adjacent side of a right-angled triangle (in this case, B_H) to the hypotenuse (B), given an angle (δ). Since BH lies along the horizontal plane, it’s the ‘adjacent side’ when considering the angle of dip.
The horizontal component is crucial when calculating other aspects of the Earth’s magnetic field, such as the total field strength or the magnetic inclination. It’s also used in navigation and for understanding the Earth’s magnetosphere.
For example, when pilots navigate using magnetic compasses, they need to consider H to ensure they’re on the correct heading. Similarly, wildlife that navigates using the Earth’s magnetic field, like migratory birds, are likely attuned to this component.
(iv) Vertical Component (V): The part of the magnetic field that runs perpendicular to the Earth’s surface.
The vertical component of Earth’s magnetic field is the part of the field that points directly down into the ground or directly up out of the Earth, depending on your location. It’s perpendicular to the horizontal component (H) and is a key factor in determining the overall shape and direction of the magnetic field lines.
If you could see Earth’s magnetic field lines, they would emerge from the southern hemisphere, curve through space, and re-enter the Earth in the northern hemisphere. At the poles, these lines are nearly vertical, which means the vertical component (V) is at its maximum. At the equator, the field lines are parallel to the surface, so the vertical component (V) is zero.
To measure the vertical component, scientists use instruments like fluxgate magnetometers. These devices can isolate (V) from the total magnetic field and provide precise measurements of its strength at various locations on Earth’s surface.
The strength of the vertical component can be calculated using the total magnetic field strength (B) and the angle of dip (δ). The formula is:
\(\displaystyle B_V = B \sin \delta \)
- B is the total magnetic field strength.
- δ is the angle of dip, which is the angle between the total magnetic field and the horizontal plane.
The sine function is used because it relates the opposite side of a right-angled triangle (in this case, BV) to the hypotenuse (B), given an angle (δ). Since BV is perpendicular to the Earth’s surface, it’s the ‘opposite side’ when considering the angle of dip.
The vertical component is crucial for understanding how the Earth’s magnetic field interacts with solar winds and cosmic rays. It also plays a significant role in the auroras near the poles, where the vertical component guides charged particles from the Sun into the Earth’s atmosphere, resulting in beautiful light displays.
So, the vertical component (V) of Earth’s magnetic field is a fundamental aspect of geomagnetism. It’s the part of the magnetic field that points vertically and varies from zero at the equator to its maximum at the poles.
Meaning of True North:
True North, also known as geographic north or geodetic north, is the direction along the Earth’s surface towards the geographic North Pole. It’s the point where the Earth’s axis of rotation intersects the Earth’s surface in the Northern Hemisphere.
True North is different from magnetic north, which is the direction that a compass needle points. Magnetic north can vary from place to place and over time due to changes in the Earth’s magnetic field.
True North is crucial for accurate navigation and mapping. It provides a constant reference point that can be used to orient maps and navigate using the stars. When navigators or GPS systems refer to “north,” they usually mean True North.
To find True North, you can use a compass and adjust for the local magnetic declination, which is the angle between magnetic North and True North at your location. Alternatively, you can use the position of the stars, like Polaris (the North Star), which lies almost directly above the North Pole.
In physics, understanding True North is part of learning about the Earth’s rotation, coordinate systems, and magnetic fields. So, True North is a fundamental concept in navigation and Earth sciences. It’s the fixed point on the globe that helps us determine direction and position, separate from the shifting magnetic north.
Meaning of Magnetic North:
Magnetic North is the direction that the needle of a compass points to, which is approximately towards the Earth’s North Magnetic Pole. It’s important to note that this is not the same as True North, which is the direction towards the geographic North Pole.
A compass works because its magnetic needle aligns with the Earth’s magnetic field. Since the Earth itself acts like a giant magnet with a magnetic field extending from pole to pole, the compass needle is drawn towards the North Magnetic Pole.
Magnetic North is crucial for navigation, especially before the advent of modern GPS technology. Explorers, hikers, and sailors have relied on compasses to find their way for centuries. The ability of a compass needle to consistently point towards Magnetic North has been a fundamental tool for orientation.
While True North is a fixed point on the globe, Magnetic North moves over time. This movement is due to changes in the Earth’s magnetic field, which is generated by the movement of molten iron in the planet’s outer core. The location of the North Magnetic Pole shifts slightly each year.
Because there is a difference between Magnetic North and True North, navigators must adjust their compass readings by a certain angle known as magnetic declination. This angle varies depending on your location on the Earth’s surface.
Magnetic North is not only different from True North but also changes over time. These changes can be gradual or, over geological timescales, quite dramatic, such as when the magnetic poles reverse. Understanding Magnetic North is not just about knowing where it is now, but also about understanding how it can change.
In simple terms, Magnetic North is the direction that a compass needle points towards, which aligns with the Earth’s magnetic field. It’s a dynamic point that can move and even flip completely, differing from the fixed geographic North Pole.
The Formula for Earth’s Magnetic Field
The Earth’s magnetic field at any location can be described by its total intensity B, which is the combination of two perpendicular components: the horizontal component BH and the vertical component BV. The angle between B and the horizontal plane is known as the Angle of Dip (δ).
Horizontal Component (BH) is the part of the magnetic field that lies parallel to the Earth’s surface. Vertical Component BV is the part of the magnetic field that points straight down into the Earth or straight up out of it.
The tangent of the angle of dip is the ratio of the vertical component to the horizontal component:
\(\displaystyle \tan \delta = \frac{B_V}{B_H} \)
The sine of the angle of dip is the ratio of the vertical component to the total magnetic field:
\(\displaystyle \sin \delta = \frac{B_V}{B} \)
The cosine of the angle of dip is the ratio of the horizontal component to the total magnetic field:
\(\displaystyle \cos \delta = \frac{B_H}{B} \)
From trigonometry, we know that the square of the sine plus the square of the cosine of an angle equals 1:
\(\displaystyle \sin^2 \delta + \cos^2 \delta = 1 \)
Substituting the expressions for sine and cosine in terms of BV and BH, we get:
\(\displaystyle \left(\frac{B_V}{B}\right)^2 + \left(\frac{B_H}{B}\right)^2 = 1 \)
Multiplying through by (B2) gives us:
\(\displaystyle B_V^2 + B_H^2 = B^2 \)
Taking the square root of both sides, we find the expression for the total magnetic field intensity (B):
\(\displaystyle B = \sqrt{B_H^2 + B_V^2} \)
This formula tells us that the total strength of the Earth’s magnetic field is the square root of the sum of the squares of its horizontal and vertical components. It’s a fundamental concept that helps us understand the three-dimensional nature of Earth’s magnetic environment.
The Earth’s magnetic field is a vector field with both magnitude and direction, and its total intensity at any point can be calculated using the horizontal and vertical components. This understanding is crucial for applications like navigation, where knowing the precise direction and strength of the magnetic field is essential.
Also Read: Torque on Current Loop, Magnetic Dipole
Variations in Earth’s Magnetic Field
The Earth’s magnetic field isn’t constant; it changes due to various factors. Here are some key variations:
- Secular Variation: The magnetic axis of the Earth slowly changes its orientation over time. This is due to the Earth’s spin and the fluid motion of its molten outer core. The cycle of this variation is about 960 years.
- Eleven-year Sunspot Cycle: Every eleven years, the number of sunspots—regions of strong magnetic fields on the Sun—peaks. These sunspots can affect the Earth’s magnetic field because they influence the amount of solar radiation and charged particles reaching our planet.
- Daily and Annual Variation: The Earth’s magnetic field experiences daily and yearly changes. Ultraviolet rays from the Sun ionize the Earth’s atmosphere, which generates currents and, consequently, magnetic fields. These variations are most noticeable in the ionosphere and can affect communication systems.
- Lunar Variations: The Moon also affects the Earth’s magnetic field. The Moon’s gravitational pull affects the Earth’s ionosphere, especially during lunar eclipses, causing variations in the magnetic field.
- Irregular and Aperiodic Variation: Sometimes, the Earth’s magnetic field experiences sudden, unpredictable changes. Increased solar activity can cause more intense ionization in the Earth’s atmosphere, leading to stronger currents and magnetic fields.
The Earth’s magnetic field is dynamic, influenced by celestial bodies like the Sun and Moon, and by the activity within its core. These variations are important to understand because they can affect navigation, satellite operations, and even animal migration patterns.
Solved Examples
Problem 1: How does the Dynamo Effect relate to other celestial bodies?
The Dynamo Effect is not unique to Earth; it’s a universal process that can occur in various celestial bodies, including planets, moons, stars, and even asteroids. The Dynamo Effect describes how a rotating, convecting, and electrically conducting fluid can maintain a magnetic field over astronomical time scales. This theory is used to explain the magnetic fields of many celestial bodies.
Planets and Moons: Just like Earth, other planets such as Mercury and the gas giants (Jupiter, Saturn, Uranus, and Neptune) have magnetic fields generated by dynamo processes in their cores. For instance, Jupiter’s strong magnetic field is attributed to the dynamo effect occurring in its metallic hydrogen core.
The Moon and Mars also show evidence of past magnetic fields, suggesting they once had dynamo activity in their cores. Although Mars does not have a global magnetic field today, magnetized rocks on its surface indicate it had a strong field billions of years ago.
Stars: Stars, including our Sun, generate magnetic fields through the dynamo effect as well. In stars, the conducting fluid is the plasma that makes up the star’s outer layers. The rotation of the star and the convection of plasma contribute to the generation of the magnetic field.
Small Celestial Bodies: Recent discoveries have complicated our understanding of the dynamo theory. For example, magnetized rocks from ancient meteorites and an active dynamo field on Mercury suggest that even small or quickly cooling celestial bodies can generate self-sustaining magnetic fields.
The Dynamo Effect is a fundamental process that shapes the magnetic properties of celestial bodies across the universe. Understanding the dynamo effect in celestial bodies helps us infer their internal structures and histories. A magnetic field indicates the presence of a metallic core, which in turn suggests a history of large-scale melting and differentiation.
Problem 2: At a certain location, the Earth’s total magnetic field (B) is (50 µT), and the angle of dip is (60∘). Calculate the horizontal and vertical components of the Earth’s magnetic field.
Solution: The horizontal component (BH) and vertical component (BV) of the Earth’s magnetic field can be calculated using the formulas:
\(\displaystyle B_H = B \cos \delta \)
\(\displaystyle B_V = B \sin \delta \)
Given:\(\displaystyle B = 50 \, \mu\text{T} = 50 \times 10^{-6} \, \text{T} \); (ẟ= 60∘)
\(\displaystyle B_H = 50 \times 10^{-6} \cos 60^\circ \)
\(\displaystyle B_H = 50 \times 10^{-6} \times \frac{1}{2} \)
\(\displaystyle B_H = 25 \times 10^{-6} \, \text{T} \)
\(\displaystyle B_V = 50 \times 10^{-6} \sin 60^\circ \)
\(\displaystyle B_V = 50 \times 10^{-6} \times \frac{\sqrt{3}}{2} \)
\(\displaystyle B_V = 25\sqrt{3} \times 10^{-6} \, \text{T} \)
\(\displaystyle B_V \approx 43.3 \times 10^{-6} \, \text{T} \)
The horizontal component is (25 µT) and the vertical component is (43.3 µT).
Problem 3: The horizontal and vertical components of the Earth’s magnetic field at a location are (30 µT) and (40 µT) respectively. Calculate the angle of dip at this location.
Solution: The angle of dip (ẟ) can be calculated using the formula:
\(\displaystyle \tan \delta = \frac{B_V}{B_H} \)
Given: BH = 30 µT, BV = 40 µT.
\(\displaystyle \tan \delta = \frac{40 \times 10^{-6}}{30 \times 10^{-6}} \)
\(\displaystyle \tan \delta = \frac{40}{30} \)
\(\displaystyle \tan \delta = \frac{4}{3} \)
\(\displaystyle \delta = \tan^{-1} \left( \frac{4}{3} \right) \)
\(\displaystyle \delta \approx 53.13^\circ \)
The angle of dip at this location is approximately (53.13∘).
Problem 4: At a location, the horizontal component of the Earth’s magnetic field is ( 20 µT), and the angle of dip is (45∘). Calculate the total magnetic field at this location.
Solution: The total magnetic field (B) can be calculated using the horizontal component (BH) and the angle of dip (ẟ ) with the formula:
\(\displaystyle B = \frac{B_H}{\cos \delta} \)
Given:\(\displaystyle B_H = 20 \, \mu\text{T} = 20 \times 10^{-6} \, \text{T}\), (ẟ= 45∘)
\(\displaystyle B = \frac{20 \times 10^{-6}}{\cos 45^\circ} \)
\(\displaystyle B = \frac{20 \times 10^{-6}}{\frac{1}{\sqrt{2}}} \)
\(\displaystyle B = 20 \times 10^{-6} \times \sqrt{2} \)
\(\displaystyle B \approx 28.28 \times 10^{-6} \, \text{T} \)
The total magnetic field at this location is approximately (28.28 µT).
Problem 5: If the total magnetic field of the Earth at a certain place is (60 µT) and the horizontal component is (30 µT), find the inclination or dip angle at that place.
Solution: The angle of dip (ẟ) can be calculated using the formula:
\(\displaystyle \sin \delta = \frac{B_V}{B} \)
First, we find (BV):
\(\displaystyle B^2 = B_H^2 + B_V^2 \)
\(\displaystyle B_V = \sqrt{B^2 – B_H^2} \)
Given: \(\displaystyle B = 60 \, \mu\text{T} = 60 \times 10^{-6} \, \text{T}\); \(\displaystyle B_H = 30 \, \mu\text{T} = 30 \times 10^{-6} \, \text{T}\)
\(\displaystyle B_V = \sqrt{(60 \times 10^{-6})^2 – (30 \times 10^{-6})^2} \)
\(\displaystyle B_V = \sqrt{3600 \times 10^{-12} – 900 \times 10^{-12}} \)
\(\displaystyle B_V = \sqrt{2700 \times 10^{-12}} \)
\(\displaystyle B_V = 51.96 \times 10^{-6} \, \text{T} \)
Now, calculate (ẟ):
\(\displaystyle \tan \delta = \frac{B_V}{B_H} \)
\(\displaystyle \tan \delta = \frac{51.96 \times 10^{-6}}{30 \times 10^{-6}} \)
\(\displaystyle \tan \delta = 1.732 \)
\(\displaystyle \delta = \tan^{-1} (1.732) \)
\(\displaystyle \delta \approx 60^\circ \)
The inclination or dip angle at that place is approximately (60∘).
Problem 6: At a location, the total magnetic field of the Earth is (50 µT), and the inclination (dip angle) is (30∘). Find the horizontal and vertical components of the Earth’s magnetic field at this location.
Solution: The horizontal component (BH) and vertical component (BV) of the Earth’s magnetic field can be calculated using the total magnetic field (B) and the angle of dip (ẟ):
\(\displaystyle B_H = B \cos \delta \)
\(\displaystyle B_V = B \sin \delta \)
Given: \(\displaystyle B = 50 \, \mu\text{T} = 50 \times 10^{-6} \, \text{T}\); (ẟ= 30∘)
\(\displaystyle B_H = 50 \times 10^{-6} \cos 30^\circ \)
\(\displaystyle B_H = 50 \times 10^{-6} \times \frac{\sqrt{3}}{2} \)
\(\displaystyle B_H = 25\sqrt{3} \times 10^{-6} \, \text{T} \)
\(\displaystyle B_H \approx 43.3 \times 10^{-6} \, \text{T} \)
\(\displaystyle B_V = 50 \times 10^{-6} \sin 30^\circ \)
\(\displaystyle B_V = 50 \times 10^{-6} \times \frac{1}{2} \)
\(\displaystyle B_V = 25 \times 10^{-6} \, \text{T} \)
The horizontal component is (43.3 µT) and the vertical component is (25 µT).
FAQs
What is the Earth’s magnetic field?
The Earth’s magnetic field, also known as the geomagnetic field, is the magnetic field that extends from the Earth’s interior out into space. It is generated by the movement of molten iron and other metals in the Earth’s outer core and acts like a giant bar magnet with a magnetic north and south pole.
How does the Earth’s magnetic field protect us?
The Earth’s magnetic field protects us by deflecting charged particles from the sun, known as the solar wind, and cosmic rays from outer space. This protective barrier called the magnetosphere, prevents these harmful particles from stripping away the atmosphere and reaching the surface.
Why does the Earth have a magnetic field?
The Earth’s magnetic field is generated by the dynamo effect, which is the result of the motion of conductive fluids in the Earth’s outer core. The movement of these fluids generates electric currents, which in turn produce magnetic fields. The combination of these fields creates the overall geomagnetic field.
What are the magnetic poles, and how do they differ from the geographic poles?
The magnetic poles are the points on the Earth’s surface where the geomagnetic field is vertical. The magnetic north pole is where the field lines point straight down, and the magnetic south pole is where they point straight up. These differ from the geographic poles, which are the fixed points where the Earth’s axis of rotation meets the surface.
How do compasses work in relation to the Earth’s magnetic field?
Compasses work by aligning a magnetized needle with the Earth’s magnetic field. The needle points towards the magnetic north pole, which allows navigators to determine direction. Because the magnetic poles shift over time, compass readings must sometimes be adjusted for magnetic declination.
What is magnetic declination?
Magnetic declination is the angle between magnetic north (the direction a compass needle points) and true north (the direction along the Earth’s surface towards the geographic North Pole). This angle varies depending on where you are on the Earth’s surface and changes over time due to the movement of the magnetic poles.
How does the Earth’s magnetic field vary over time?
The Earth’s magnetic field varies over time due to changes in the flow of molten metals in the outer core. These changes can cause the magnetic poles to wander and even reverse, a phenomenon known as geomagnetic reversal. Additionally, the strength of the magnetic field can fluctuate over periods ranging from years to millennia.