The concept of materials expanding with heat has likely been observed since ancient times, as people noticed that hot days could cause doors to stick or metals to become more pliable.
The scientific study of thermal expansion began during the Renaissance. This period marked the birth of modern science, with scholars starting to quantify and create theories about natural phenomena.
In the 17th Century, Robert Hooke was among the first to suggest using the freezing point of water as a reference point for temperature measurement, which is crucial for understanding thermal expansion.
Then Ole Christensen Rømer proposed the idea of using fixed points, like the freezing and boiling points of water, to create a temperature scale, which helped in studying thermal expansion.
The invention of thermometers, which used liquids like alcohol or mercury, allowed for more precise measurements of temperature changes and, consequently, thermal expansion. The development of gas laws and the concept of absolute zero provided a deeper understanding of how substances expand and contract with temperature changes.
Today, thermal expansion is a well-understood phenomenon with applications in everyday technology, from the design of bridges and railways to the functioning of thermostats and electronic devices.
What is Thermal Expansion?
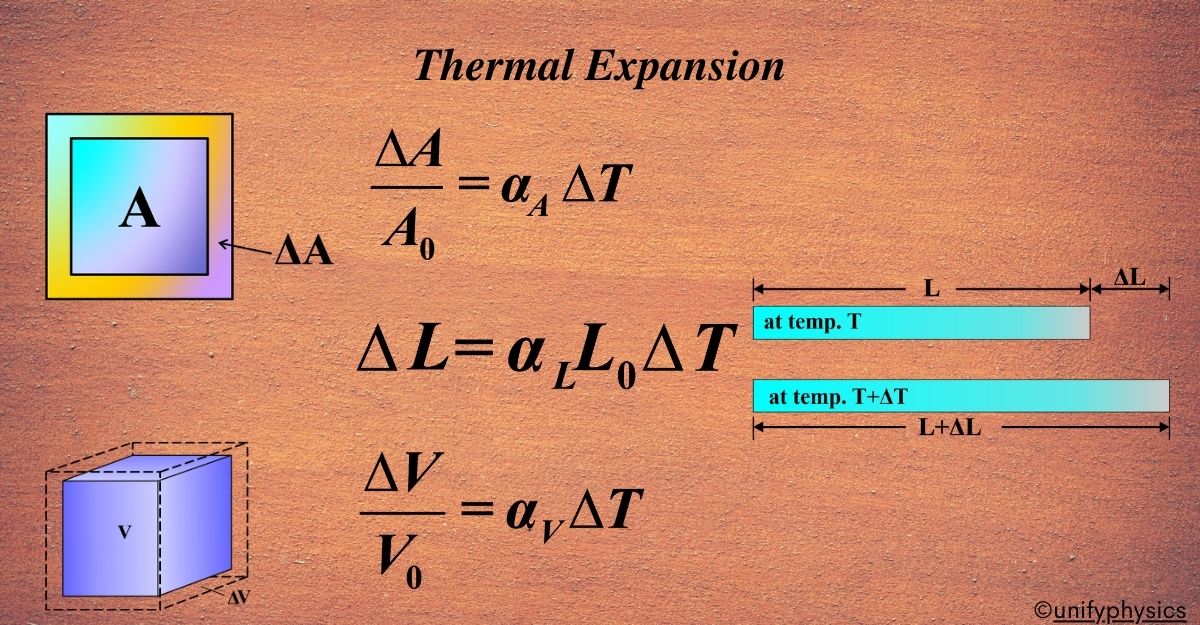
Thermal expansion is a phenomenon that occurs in solids, liquids, and gases. When heat is applied to an object or body, it undergoes expansion. This expansion refers to the change in dimension, such as length, density, area, or volume, caused by the increase in temperature. As the substance is heated, its kinetic energy rises, leading to thermal expansion.
“The increase in the dimensions of a body due to the increase in its temperature is called thermal expansion.”
Thermal expansion is of three types:
- Linear Expansion
- Area Expansion
- Volume Expansion
Also Read: Heat
Linear expansion
This is an expansion in the dimension of the length of a solid body. It takes place only in solids. To explain linear expansion, we take a simple example of a ruler scale. Figure shows a ruler scale of length L at temperature T. If the temperature of scale increases, due to thermal expansion, its length also increases. It is observed that on increasing temperature by ΔT, the expansion in its length ΔL is directly proportional to the rise in temperature ΔT as

Notably, larger objects tend to experience more expansion due to the greater number of molecules involved. The increase in intermolecular spacing occurs uniformly, leading to proportional changes in dimensions. Therefore, we can conclude that the expansion in length, denoted as ΔL, is directly proportional to the initial length of the scale.
\(\displaystyle \Delta L \propto \Delta T \)
\(\displaystyle \Delta L \propto L \)
\(\displaystyle \Delta L \propto L\Delta T \)
\(\displaystyle \Delta L = \alpha L\Delta T \)
\(\displaystyle L_{f} = L + \Delta L \)
\(\displaystyle L_{f} = L(1 + \alpha \Delta T)\)
Where, α – is the proportionality constant which depends on the material of the body is called the coefficient of linear expansion.
Theoretically, α is a constant. However, in practice, it has been observed that the value of α varies with temperature. Additionally, the relationship between α and temperature can also change depending on the temperature range being considered. But for a short range of temperature α can be taken as a constant.
Coefficient of Linear Expansion
The coefficient of linear expansion refers to a material’s property that quantifies how much its length changes when subjected to a change in temperature. It represents the fractional change in length per degree of temperature change and is a significant factor in understanding how materials respond to thermal fluctuations.
“Coefficient of Linear Expansion is the rate of change of unit length per unit degree change in temperature”
The coefficient of linear expansion can be mathematically written as
\(\displaystyle {{\alpha }_{L}}=\frac{{\frac{{dL}}{{dT}}}}{{{{L}_{0}}}}\) or \(\displaystyle \frac{{\Delta L}}{{{{L}_{0}}}}={{\alpha }_{L}}\Delta T\)
The linear expansion coefficient is an intrinsic property that characterizes the behavior of each material and, as such, it varies from one material to another. This coefficient determines how much a material’s length will change when subjected to a temperature increase. The expansion rate largely relies on the cohesive force between the atoms within the material. Cohesive force represents the binding force between two or more atoms, resisting their separation.
In simpler terms, cohesive force hinders the atoms from moving apart. When cohesive force is strong, the expansion of a material will be relatively low for a given rise in temperature. Conversely, materials with weaker cohesive forces will experience more significant expansion with a unit increase in temperature.
Soft metals, like Lead, possess low melting points and can be easily compressed. Due to these characteristics, when heated, Lead will exhibit faster expansion with each incremental rise in temperature. This behavior highlights how a material’s intrinsic properties, such as its cohesive force and melting point, significantly influence its response to changes in temperature and subsequent expansion.
Area Expansion
The area thermal expansion coefficient is a measure that links changes in temperature to alterations in the area dimensions of a material. It represents the fractional change in area for every degree of temperature change. Area expansion pertains to the broadening or enlarging an object’s surface, essentially increasing the space occupied by its surface.

This two-dimensional material expansion is dependent on the temperature of the object. Whenever the temperature changes, causing the volume of the object to change, the area expands accordingly.
\(\displaystyle \frac{{\Delta A}}{{{{A}_{0}}}}={{\alpha }_{A}}\Delta T\)
Regardless of the object’s initial size, its length, volume, and area change due to thermal expansion. The extent of area expansion is directly proportional to the temperature change. The rate of expansion is influenced by two crucial factors: temperature and material properties. Kinetic energy facilitates the expansion of the material, contributing to its enlargement as the temperature increases. In essence, area expansion showcases how materials respond to thermal fluctuations by stretching their surface area and adapting to changes in temperature.
Coefficient of Area Expansion
The coefficient of area expansion, denoted by the symbol “αA” is a measure that quantifies the relationship between the change in area of an object and the corresponding temperature change. It represents the extent to which the area of a substance expands or contracts as the temperature increases or decreases.
When the coefficient of area expansion is positive (αA > 0), it means that the area of the object increases with a temperature rise. As the temperature increases, the particles within the material gain energy and move more vigorously, increasing the average distance between them. This increase in inter-particle spacing leads to the expansion of the material’s area. Conversely, when the coefficient of area expansion is negative (αA < 0), it indicates that the area of the object decreases as the temperature rises. In such cases, the particles in the material contract and move closer together as the temperature increases, causing the area to reduce.
Volume Expansion
Volume expansion, also known as volumetric expansion, is the phenomenon where the volume of a material increases with an increase in temperature and decreases with a decrease in temperature.
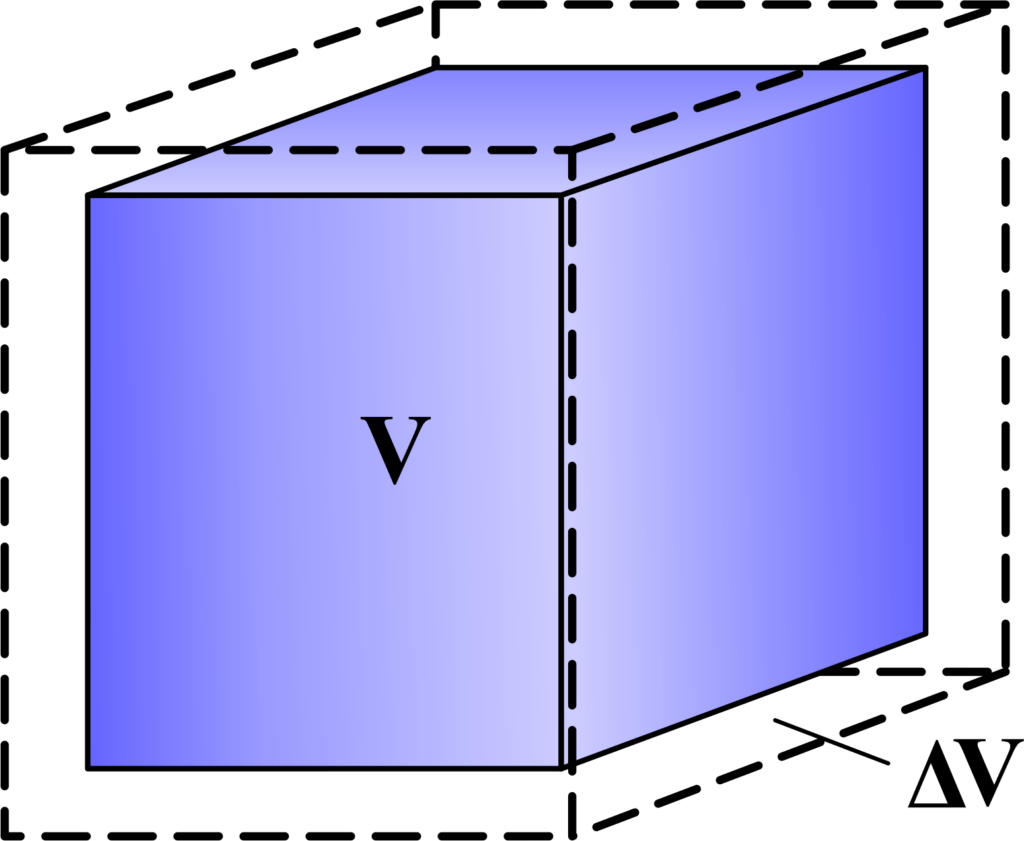
Like linear and area expansion, volume expansion is a result of the response of materials to changes in thermal energy.
Despite the temperature change, the expansion coefficient remained constant, resulting in a relatively minor increase in volume compared to the original volume.
Coefficient of Volume Expansion
The degree of volume expansion divided by the temperature change is known as the coefficient of volume expansion (αV).
\(\displaystyle \frac{{\Delta V}}{{{{V}_{0}}}}={{\alpha }_{V}}\Delta T\)
This coefficient varies for different materials and provides insight into how much a material’s volume will change for a given change in temperature. When the coefficient of volume expansion is positive (αV> 0), the volume of the material increases with increasing temperature. Conversely, when it is negative (αV < 0), the volume decreases with increasing temperature.
Thermal Expansion of Solids, Liquids and Gases
Thermal expansion is a natural phenomenon that causes bodies to change their dimensions, including length, area, density, or volume, in response to changes in temperature. When a substance is heated, the kinetic energy of its particles increases, leading to their increased movement and separation from one another.
Solid: Solids are characterized by tightly packed particles with minimal gaps between them, making them highly resistant to compression. Their shape and volume remain fixed, and they exhibit rigidity, with particles only vibrating about their mean positions. The attractive forces between solid particles are unyielding, contributing to their stable structure. Examples of solids include ice, wood, sugar, and rocks.
Liquid: In contrast to solids, the particles in liquids are less tightly packed, allowing them to flow and take the shape of their container. While liquids still have less space between their particles compared to gases, their compression is not as challenging as in solids. Liquids have a fixed volume but can adapt to various shapes. Diffusion in liquids occurs more readily than in solids due to the increased freedom of movement. Common examples of liquids are water, milk, coffee, and blood.
Gas: Gaseous particles are much farther apart, and the force of attraction between them is nearly negligible, allowing them to move independently and freely. Gases have no fixed shape or volume and readily expand to fill the available space. Their high level of particle mobility makes gases easy to compress. Diffusion in gases occurs at a faster rate compared to both solids and liquids. Examples of gases include air, oxygen, nitrogen, and carbon dioxide.
Solve Examples
Example 1: A steel rod of length 2 meters and initial temperature 20°C is heated until its length becomes 2.01 meters. Calculate the change in length if the coefficient of linear expansion of steel is (1.2 ×10-5/°C).
Solution: Given, Initial length, (L0 = 2) m ; Final length, (L = 2.01) m ; Initial temperature, (T0 = 20°C) ; Coefficient of linear expansion, (α = 1.2 \times 10-5/°C)
Change in length, (∆ L = L – L0 ). Using the formula for linear expansion:
\(\displaystyle \Delta L = L_0 \alpha (T – T_0) \)
Substituting the given values:
\(\displaystyle \Delta L = (2 \, \text{m}) \times (1.2 \times 10^{-5}/°C) \times (T – 20°C) \)
When the length becomes 2.01 meters, the temperature change (T – T0) is:
\(\displaystyle \Delta L = (2 \, \text{m}) \times (1.2 \times 10^{-5}/°C) \times (T – 20°C) = 0.01 \, \text{m} \)
\(\displaystyle T – 20°C = \frac{0.01 \, \text{m}}{(2 \, \text{m}) \times (1.2 \times 10^{-5}/°C)} \)
\(\displaystyle T – 20°C = 4166.67 \, \text{°C} \)
Therefore, the final temperature is (T = 4186.67°C), and the change in length is (0.01) meters.
Example 2: A brass rod of length 1 meter at 20°C is heated to 120°C. If the coefficient of linear expansion of brass is (2.0 × 10-5/°C), calculate the change in length.
Solution: Given, Initial length, (L0 = 1) m ; Initial temperature, (T_0 = 20°C) ; Final temperature, (T = 120°C) ; Coefficient of linear expansion, (α = 2.0 × 10-5/°C)
Using the formula for linear expansion:
\(\displaystyle \Delta L = L_0 \alpha (T – T_0) \)
Substituting the given values:
\(\displaystyle \Delta L = (1 \, \text{m}) \times (2.0 \times 10^{-5}/°C) \times (120°C – 20°C) \)
\(\displaystyle \Delta L = (1 \, \text{m}) \times (2.0 \times 10^{-5}/°C) \times (100°C) = 0.002 \, \text{m} \)
Therefore, the change in length is (0.002) meters.
Example 3: A copper wire of length 3 meters and initial temperature 25°C is cooled until its length becomes 2.99 meters. If the coefficient of linear expansion of copper is (1.7 × 10-5/°C), calculate the temperature change.
Solution: Given, Initial length, (L0 = 3) m ;Final length, (L = 2.99) m; Initial temperature, (T0 = 25°C);
Coefficient of linear expansion, (α = 1.7 × 10-5/°C)
Using the formula for linear expansion:
\(\displaystyle \Delta L = L_0 \alpha (T – T_0) \)
We need to find the temperature change (T – T0).
\(\displaystyle \Delta L = (3 \, \text{m}) \times (1.7 \times 10^{-5}/°C) \times (T – 25°C) = -0.01 \, \text{m} \)
\(\displaystyle T – 25°C = \frac{-0.01 \, \text{m}}{(3 \, \text{m}) \times (1.7 \times 10^{-5}/°C)} \)
\(\displaystyle T – 25°C ≈ -1960.78 \, \text{°C} \)
Therefore, the final temperature is (T ≈ 2039.22°C), and the temperature change is approximately (-1960.78°C).
FAQs
Why do train tracks have gaps between them, especially in hot climates?
Train tracks are made of metal, which expands when heated. In hot weather, the metal tracks expand, and without gaps, they might buckle or warp. The gaps allow for the expansion without causing damage.
Why do some substances expand more than others when heated?
The extent to which a substance expands when heated depends on its coefficient of thermal expansion, which is unique to each material. Substances with higher coefficients expand more compared to those with lower coefficients. This is due to differences in the atomic structure and bonding within the material.
How does thermal expansion affect bridges and large structures?
Large structures like bridges are designed with expansion joints to accommodate thermal expansion. Without these joints, the expansion of the materials due to temperature changes could cause stress, leading to structural damage or failure.
Why do glass objects such as bottles crack when exposed to sudden temperature changes?
Glass has a relatively low coefficient of thermal expansion compared to other materials. When subjected to rapid temperature changes, such as pouring hot liquid into a cold glass or vice versa, different parts of the glass expand or contract at different rates, leading to internal stress and potential cracking.
Why are expansion loops installed in pipelines?
Expansion loops are installed in pipelines to accommodate the thermal expansion and contraction of the materials due to temperature changes. Without these loops, the pipes could experience stress, leading to leaks or structural damage. Expansion loops provide flexibility, allowing the pipeline to expand and contract without causing damage to the system.