Thermodynamic Equilibrium

The journey into understanding thermodynamic equilibrium began in the 19th century. It was a time when steam engines were transforming the world, and scientists were curious about how to make them more efficient. This curiosity led to the birth of thermodynamics as a field of study.

Sadi Carnot, often called the “father of thermodynamics,” laid the groundwork with his reflections on the power of heat in 1824. He pondered on how to get the best work out of steam engines and introduced the concept of a Carnot cycle, which is a theoretical model that defines the maximum possible efficiency a heat engine can achieve.

Rudolf Clausius and William Thomson (Lord Kelvin) further developed these ideas, leading to the formulation of the first and second laws of thermodynamics. Clausius introduced the concept of entropy in 1865, which is a measure of disorder or randomness in a system.

Josiah Willard Gibbs, an American scientist, brought a monumental change by introducing the concept of chemical potential and free energy. His work in the late 19th century provided a way to predict whether a chemical reaction would occur spontaneously.

Thermodynamic equilibrium became a cornerstone concept, defining a state where a system is perfectly balanced—no net flows of matter or energy, no changes in pressure, temperature, or composition. It’s like a perfectly calm day where everything is still, and nothing changes unless an external force acts upon it.

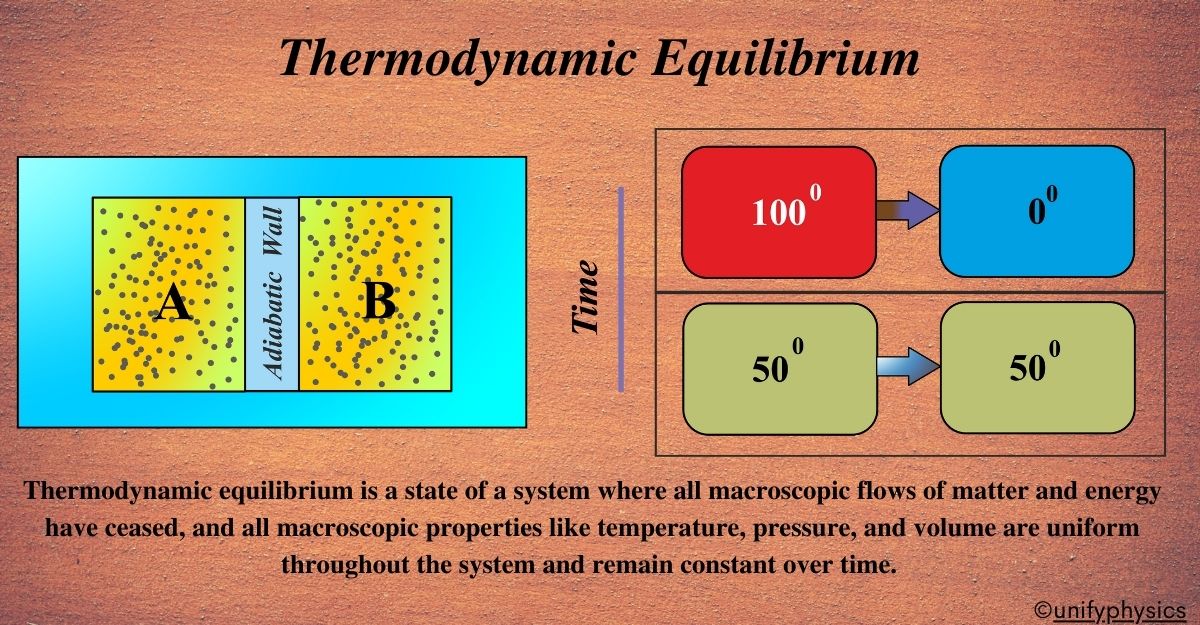
What is Thermodynamic Equilibrium

Thermodynamic Equilibrium is a state where a system’s macroscopic properties like pressure, temperature, and volume are uniform throughout and do not change over time. It’s like a calm sea where the water is still, and there are no waves or currents.

Thermodynamic equilibrium is a state in which a thermodynamic system, whether it’s a simple gas or a complex industrial process, has reached a condition where its properties—such as temperature, pressure, and density—remain uniform and constant over time. In this state, there is no net flow of matter or energy within the system or between the system and its surroundings.

In thermodynamic equilibrium, the macroscopic properties of the system do not undergo any net change. Temperature, pressure, and other relevant parameters remain constant. While it’s a state of apparent stillness, thermodynamic equilibrium doesn’t mean that individual particles within the system are static. There’s a dynamic balance with particles still moving and interacting, but these movements result in no net change at the macroscopic level.

Imagine you have a room with air spread out evenly, and the temperature is the same everywhere. This room is like a system in Thermodynamic Equilibrium. It’s a state where everything in the system is balanced and stable. There are no drafts of wind (no net flow of matter) and no spots that are hotter or colder than others (no net flow of energy). Everything is calm and unchanging.

In more scientific terms, Thermodynamic Equilibrium is when a system’s properties, such as temperature, pressure, and volume, are uniform and constant over time. It’s like having a perfectly even and still pond where every part of the water is at rest relative to every other part.

• If you have a hot cup of coffee in a room, initially, the coffee is hot, and the room is cooler.
• Over time, the heat from the coffee spreads out into the room until the coffee and the room are at the same temperature.
• When they reach the same temperature, and there’s no more heat flowing from the coffee to the room, they are in Thermal Equilibrium.
• If the coffee cup is also not moving and no chemical reactions are happening in the coffee, then the coffee and the room are in Thermodynamic Equilibrium.

So, Thermodynamic Equilibrium is like a state of perfect peace in a system where nothing is changing, and if you want to change anything, you have to put in some effort or energy.

types of thermodynamic equilibrium

There are several types of thermodynamic equilibrium, each dealing with specific aspects.

Chemical Equilibrium

Chemical equilibrium stands as a cornerstone concept in the study of chemical reactions, offering profound insights into the dynamic nature of molecular transformations. For 12th-grade physics students venturing into the realm of chemistry, comprehending the principles governing chemical equilibrium is essential.

The Nature of Chemical Equilibrium:

In a system undergoing a chemical reaction, chemical equilibrium is attained when the rates of the forward and reverse reactions reach an equilibrium state. Contrary to popular belief, equilibrium does not imply that reactions cease; rather, it signifies a dynamic balance where the rates of both forward and reverse reactions are equal. Despite continuous transformations between reactants and products, there is no net change in their concentrations, thus maintaining stability within the system.

For every chemical reaction at equilibrium, there exists an equilibrium constant (K) that quantitatively expresses the ratio of product concentrations to reactant concentrations. This constant serves as a crucial predictive tool, offering insights into the direction in which the reaction will proceed. By analyzing the equilibrium constant, scientists can discern whether a reaction favors the formation of products or the consumption of reactants under given conditions.

Imagine a busy marketplace where people are constantly buying and selling goods. Now, if at any given moment, the number of items being bought is equal to the number of items being sold, the market is said to be in a state of balance. This is similar to what happens in a chemical reaction at equilibrium.

In chemistry, Chemical Equilibrium is like that balanced marketplace but with molecules. It’s a state in a chemical reaction where the rate at which the reactants are turning into products is the same as the rate at which the products are turning back into reactants⁶. This doesn’t mean the reactions have stopped; they’re still happening, but the amounts of reactants and products remain constant over time.

Let’s take a simple chemical reaction where substance A and substance B react to form substance C and substance D:

\(\displaystyle A + B \rightleftharpoons C + D \)

At the start, A and B are reacting to form C and D. As C and D start to accumulate, they also begin to react with each other to recreate A and B. Eventually, the reaction reaches a point where A and B are forming C and D at the same rate C and D are forming A and B. This is the point of equilibrium.

It’s important to note that chemical equilibrium is dynamic. This means that even though the overall amounts of reactants and products stay the same, the molecules are still moving and reacting. It’s a bit like a dance where the dancers (molecules) are constantly switching partners (reacting), but the number of dancing couples (reactant and product concentrations) remains unchanged.

The conditions of the reaction, like temperature and pressure, can shift this equilibrium. If you change the conditions, it’s like changing the music in our dance analogy—the dancers might switch partners faster or slower, affecting the balance.

Mechanical equilibrium

Mechanical equilibrium is a state in which a physical system experiences no net force and is either at rest or moving with constant velocity. It is a fundamental concept in classical mechanics and is crucial for understanding the stability and motion of objects.

In a state of mechanical equilibrium, the vector sum of all external forces acting on the system is zero. This implies that there is no unbalanced force to cause linear acceleration. For systems involving rotation, mechanical equilibrium also requires that the net torque (the rotational equivalent of force) is zero. This ensures no angular acceleration or rotational motion.

Think of a book lying flat on a table. It’s not moving, right? That’s because it’s in Mechanical Equilibrium. This means that all the forces acting on the book are perfectly balanced. The table pushes up on the book with the same force that gravity is pulling it down. Since these forces are equal and opposite, the book stays still.

• Balanced Forces: In mechanical equilibrium, forces are in balance. If you push on something with the same force from opposite sides, it won’t move. That’s what’s happening with our book on the table.
• No Acceleration: Because the forces are balanced, there’s no acceleration. According to Newton’s First Law of Motion, an object at rest will stay at rest unless acted upon by an unbalanced force. So, if our book isn’t accelerating, it’s in equilibrium.
• Net Force is Zero: When we say ‘net force,’ we mean the sum of all forces acting on an object. If this sum is zero, the object is in mechanical equilibrium. For our book, the force of gravity (downward) and the force of the table (upward) cancel each other out, making the net force zero.

Types of Mechanical Equilibrium:

Static Equilibrium

In static equilibrium, the system is at rest. All forces and torques are balanced, resulting in no linear or angular motion. It’s like a book sitting on a table where the force of gravity is balanced by the normal force. An example is a book lying on a table in static equilibrium. The force due to gravity is balanced by the normal force from the table, and there is no net force or torque.

Imagine a sculpture perfectly balanced on a pedestal. No matter where you look, it’s not tipping over or spinning—it’s just still. This is what we call Static Equilibrium in physics.

In Static Equilibrium, an object is completely at rest, and two main conditions are met:

• No Net Force: The sum of all forces acting on the object is zero. It’s like a tug-of-war where both teams are equally strong, and the rope doesn’t move.
• No Net Torque: The sum of all torques (forces that cause rotation) is also zero. Think of a seesaw with two people of equal weight sitting at equal distances from the pivot point; the seesaw doesn’t tilt either way.

This means the object isn’t sliding or moving from one place to another. All the pushes and pulls cancel out. The object isn’t spinning or rotating. All the twists and turns balance each other out.

To understand static equilibrium, physicists often draw free-body diagrams. These diagrams show all the forces acting on an object with arrows. If the object is in static equilibrium, all the arrows representing forces should create a shape that closes back on itself, indicating no net force.

Translational Equilibrium: Translational Equilibrium is a state in physics where the net force acting on an object is zero, resulting in the object having zero linear acceleration. This means that the object may either be at rest or moving with a constant velocity because no unbalanced forces are causing it to accelerate.

For an object to be in translational equilibrium, the sum of all forces acting on it must be zero. This means that the object will not start moving or change its motion if it’s already moving at a constant velocity. Mathematically, we can express this as:

\(\displaystyle \sum \vec{F} = 0 \)

Here, (\(\displaystyle \sum \vec{F}\) ) represents the vector sum of all forces. If this sum equals zero, our object is in translational equilibrium.

In simpler terms, if you have forces acting on an object from different directions, and they all cancel each other out, then the object won’t start moving or change its motion. It’s like a game of tug-of-war where both teams are equally strong, and the rope stays in the middle, not moving to either side. That’s translational equilibrium — a perfect balance of forces ensuring no change in motion.

Think of a book lying flat on a table. Gravity pulls it down, and the table pushes it up with an equal force. These forces are balanced, so the book stays put.

So, Translational Equilibrium is all about balance. It’s the reason why buildings don’t collapse under their weight and why we can walk without falling over. It’s a state of perfect harmony where all the forces cancel each other out, leading to a peaceful standstill or a smooth, unchanging motion.

Example: Consider a ladder leaning against a wall without slipping. Here, the ladder finds itself in static equilibrium, with the gravitational force harmonizing seamlessly with the wall’s normal force, ensuring steadfast stability. A bridge arch that holds its shape without collapsing.

Rotational Equilibrium: Rotational Equilibrium is a state in which a system experiences no net torque and therefore has a constant rotational velocity. This means that all the torques acting on the system are balanced, resulting in no angular acceleration. In other words, the object is either stationary or rotating at a steady rate without speeding up or slowing down.

Mathematically, rotational equilibrium can be expressed as:

\(\displaystyle \sum \tau = 0 \)

Here, ( \(\displaystyle\sum \tau\) ) represents the vector sum of all torques acting on the object. If this sum equals zero, the object is in rotational equilibrium.

In simpler terms, if you have several forces trying to rotate an object around a pivot point, and they all cancel each other out, then the object won’t start spinning or change its spinning motion. It’s like a perfectly balanced wheel that spins smoothly without any wobble. That’s a rotational equilibrium — a perfect balance of rotational forces.

Imagine a spinning top that’s spinning smoothly on a table. It’s not wobbling or slowing down; it’s just spinning perfectly. This top is in Rotational Equilibrium. It means that the top is spinning at a constant speed and there’s no net torque acting on it to change its rotational velocity.

To fully grasp rotational equilibrium, we need to understand torque. A torque is like a twist or a force that causes objects to rotate. The amount of torque depends on two things: The force applied and the distance from the point where the force is applied to the axis of rotation (this distance is called the ‘lever arm’).

An object is in rotational equilibrium when:

• The sum of all torques acting on it is zero (\(\displaystyle\sum \tau = 0 \)).
• There’s no angular acceleration, which means the object is either stationary or rotating at a constant speed.

Examples: A ceiling fan running at a steady speed is in rotational equilibrium because the torques from the motor and the air resistance balance out. A balanced seesaw that’s not moving is in rotational equilibrium because the clockwise and counterclockwise torques are equal. So, Rotational Equilibrium is all about the balance of forces in rotation. It’s what keeps spinning objects steady and predictable.

Dynamic Equilibrium

In dynamic equilibrium, the system is in motion but at a constant velocity. Forces are balanced to maintain a steady speed. An example is a car moving at a constant speed on a straight road. If the driving force equals the resistive forces (friction, air resistance), the car is in dynamic equilibrium.

Imagine you’re on a skateboard, gliding smoothly down a gentle slope. You’re not speeding up or slowing down, just cruising at a constant speed. This is a real-life example of Dynamic Equilibrium in mechanics.

• Constant Velocity: In dynamic equilibrium, an object is moving, but it’s doing so at a steady pace — constant speed and direction. It’s like a car on a highway maintaining a speed of 60 km/h without accelerating or decelerating.
• Balanced Forces: Even though the object is in motion, the forces acting on it are in perfect balance. This means there’s no net force causing the object to change its state of motion.
• No Acceleration: Since the forces are balanced, according to Newton’s First Law, the object will continue in its state of motion at a constant velocity because there’s no unbalanced force to cause acceleration.

So, dynamic equilibrium is all about maintaining a consistent, unchanging motion. It’s the state of balance not just when things are still, but also when they’re on the go.

Example: Visualize a satellite gracefully orbiting the Earth, balancing the relentless pull of gravity with its tangential velocity. In this scenario, the satellite maintains dynamic equilibrium, perpetually tracing its celestial path without deviation. A fan spinning at a constant speed is in dynamic equilibrium because the electrical torque from the motor and the air resistance are equal and opposite.

Read Also: Thermal Expansion

Thermal Equilibrium

Thermal equilibrium is a state in which two or more bodies, or systems, that are in physical contact with each other, have the same temperature. In this state, there is no net flow of heat between the systems. It is a fundamental concept in thermodynamics and plays a crucial role in understanding heat transfer.

In thermal equilibrium, the temperatures of the interacting systems are equal. Temperature is a measure of the average kinetic energy of particles in a system. Thermal equilibrium implies that there is no net transfer of heat between the systems. While individual particles may exchange energy, there is no overall flow of heat.

Achieving thermal equilibrium often involves allowing the systems to interact for a sufficiently long time. It’s a reversible process where the exchange of energy reaches a balanced state. If there is a temperature difference between two systems, heat will flow from the hotter system to the cooler one until thermal equilibrium is reached. At equilibrium, the temperature gradient is zero.

Imagine you have two cups of water, one hot and one cold. If you pour them into a single container and wait a bit, you’ll notice that the water reaches a consistent temperature. This is Thermal Equilibrium—a state where the temperature is the same throughout the entire system. We look into the science behind the balance

• Uniform Temperature: In thermal equilibrium, there’s no temperature difference within the system. This means there’s no heat flow from one part to another because all parts are at the same temperature.
• Zeroth Law of Thermodynamics: This law states that if two systems are each in thermal equilibrium with a third system, then they are in thermal equilibrium with each other. It’s like saying if person A is as tall as person C, and person B is also as tall as person C, then person A and B are of the same height.
• Energy Exchange: When two objects at different temperatures come into contact, heat energy flows from the hotter object to the cooler one. This continues until both objects reach the same temperature—that’s when they’re in thermal equilibrium.
• No Net Heat Flow: Once thermal equilibrium is reached, there’s no net flow of heat between the objects. They can still exchange energy, but the exchange is equal in both directions, so there’s no overall change.

Examples:

• Placing a hot object and a cold object in contact until they reach the same temperature.
• Allowing a cup of hot coffee to cool until the coffee and the surrounding air are in thermal equilibrium.

Thermal equilibrium forms the basis for concepts like the Zeroth Law of Thermodynamics, which asserts that if two systems are each in thermal equilibrium with a third system, then they are in thermal equilibrium with each other.

Thermal equilibrium represents a balanced state where there is no spontaneous flow of heat between systems, and their temperatures are equal. This concept is foundational in the study of heat and energy transfer.

An Isolated Body’s Internal Thermal Equilibrium:

When an isolated body reaches a state where its temperature is uniform and does not change over time. Imagine you have a thermos flask that’s completely sealed and insulated. Inside, there’s a hot drink. Now, this thermos is so good that no heat can escape or enter it—it’s isolated from the rest of the world. Over time, the temperature inside the thermos becomes uniform, and then it stays that way. This is what we mean by an isolated body’s internal thermal equilibrium³.

• No External Influence: Since the body is isolated, there’s no heat exchange with the environment. It’s all about what’s happening inside the body itself.
• Uniform Temperature: Eventually, every part of the isolated body reaches the same temperature. There’s no ‘hot’ or ‘cold’ spot left; it’s all even.
• No Macroscopic Change: Once thermal equilibrium is achieved internally, you won’t see any visible changes. The temperature is stable, and if you could measure it at different points inside the body, it would be the same everywhere.

An isolated body has its intrinsic characteristics, like the specific heat capacity of the material it’s made of. These characteristics determine how the body will eventually distribute its internal energy to reach equilibrium. So, An Isolated Body’s Internal Thermal Equilibrium is about reaching a state of even temperature throughout the body without any external help. It’s like a perfectly mixed smoothie with the same flavor and temperature in every sip—nothing changes as long as it’s sealed off from the outside world.

Also Read: Thermodynamic System

Application of Thermodynamic Equilibrium

The concept of Thermodynamic Equilibrium has a wide range of applications in physics and engineering. Here are some key applications:

Heat Engines: Heat engines, like those in cars and power plants, operate by bringing a working substance (like gas or steam) through cycles of thermodynamic processes. At certain points in these cycles, the substance is brought into thermodynamic equilibrium to efficiently convert heat into work.

Refrigerators and Heat Pumps: Refrigerators and heat pumps achieve cooling effects by exploiting the principles of thermodynamic equilibrium. They transfer heat from a cooler place to a warmer place, which is against the natural direction of heat flow, by ensuring the refrigerant reaches equilibrium at different stages of the refrigeration cycle.

Predicting Chemical Reactions: In chemistry, understanding thermodynamic equilibrium allows scientists to predict whether a chemical reaction will occur spontaneously. It helps in calculating the equilibrium constant for reactions, which is crucial for industrial chemical processes.

Material Science: The study of phase transitions in materials, like melting and solidification, relies on the principles of thermodynamic equilibrium. It’s essential for designing materials with specific properties and for understanding the behavior of materials under different temperatures and pressures.

Astrophysics: In astrophysics, the concept is used to understand the life cycle of stars, which involves complex processes of nuclear fusion and gravitational collapse. Stars are often modeled as being in thermodynamic equilibrium to simplify these complex processes.

Climate Science: Thermodynamic equilibrium plays a role in climate science and meteorology. For example, the Earth’s atmosphere is often assumed to be in radiative equilibrium, which helps in modeling and predicting weather patterns.

Biological Systems: Even in biology, thermodynamic equilibrium is important for understanding processes like osmosis and diffusion across cell membranes, which are vital for cell function and homeostasis.

Solved Examples

Problem 1: Two bodies, A and B, are in thermal contact. Body A has a mass of 2 kg and a specific heat capacity of 400 J/kg·K. Body B has a mass of 3 kg and a specific heat capacity of 600 J/kg·K. Initially, the temperature of body A is (T_A = 300 K) and the temperature of body B is (T_B = 350 K). Calculate the final temperature of the system when thermal equilibrium is reached, assuming no heat is lost to the surroundings.

Solution: In thermal equilibrium, the heat lost by body B will be equal to the heat gained by body A. Let the final temperature be (T_f). Heat lost by body B:

\(\displaystyle Q_B = m_B c_B (T_B – T_f) \)
\(\displaystyle Q_B = 3 \times 600 \times (350 – T_f) \)
\(\displaystyle Q_B = 1800 \times (350 – T_f) \)

Heat gained by body A:

\(\displaystyle Q_A = m_A c_A (T_f – T_A) \)
\(\displaystyle Q_A = 2 \times 400 \times (T_f – 300) \)
\(\displaystyle Q_A = 800 \times (T_f – 300) \)

Since (Q_B = Q_A):

\(\displaystyle 1800 \times (350 – T_f) = 800 \times (T_f – 300) \)

Solve for (T_f):

\(\displaystyle 1800 \times 350 – 1800 T_f = 800 T_f – 800 \times 300 \)
\(\displaystyle 630000 – 1800 T_f = 800 T_f – 240000 \)
\(\displaystyle 630000 + 240000 = 1800 T_f + 800 T_f \)
\(\displaystyle 870000 = 2600 T_f \)
\(\displaystyle T_f = \frac{870000}{2600} \)
\(\displaystyle T_f = 334.6 \, \text{K} \)

Therefore, the final temperature of the system at thermal equilibrium is approximately (334.6 K).

Problem 2: A piston-cylinder arrangement contains an ideal gas at an initial pressure of (100 kPa) and a volume of (0.5 m³). The piston is then compressed slowly, keeping the temperature constant, until the pressure reaches (200 kPa). Calculate the final volume of the gas.

Solution: For an isothermal process (constant temperature), the ideal gas law applies:

\(\displaystyle P_1 V_1 = P_2 V_2 \)

Given: Initial pressure, (P₁ = 100 kPa); Initial volume, (V₁ = 0.5 m³); Final pressure, (P₂ = 200 kPa)

Solve for the final volume, (V₂):

\(\displaystyle V_2 = \frac{P_1 V_1}{P_2} \)
\(\displaystyle V_2 = \frac{100 \times 0.5}{200} \)
\(\displaystyle V_2 = \frac{50}{200} \)
\(\displaystyle V_2 = 0.25 \, \text{m}^3 \)

Therefore, the final volume of the gas is (0.25 m³).

Problem 3: For the reaction (\(\displaystyle \text{N}_2(g) + 3\text{H}_2(g) \rightleftharpoons 2\text{NH}_3(g) \)), the equilibrium constant (K_c) at a certain temperature is 1.6. If the initial concentrations are (\(\displaystyle [\text{N}_2] = 1 \, \text{M}), ([\text{H}_2] = 2 \, \text{M}), and ([\text{NH}_3] = 0 \, \text{M}\)), calculate the equilibrium concentrations of all species.

Solution: Let the change in concentration of (\(\displaystyle\text{N}_2\)) be (-x). Then, the change in concentration of (\(\displaystyle\text{H}_2\)) is (-3x), and the change in concentration of (\(\displaystyle\text{NH}_3) is ( +2x \)).

At equilibrium:

\(\displaystyle [\text{N}_2] = 1 – x \)
\(\displaystyle [\text{H}_2] = 2 – 3x \)
\(\displaystyle [\text{NH}_3] = 2x \)

The equilibrium constant (K_c) is given by:

\(\displaystyle K_c = \frac{[\text{NH}_3]^2}{[\text{N}_2][\text{H}_2]^3} \)
\(\displaystyle 1.6 = \frac{(2x)^2}{(1 – x)(2 – 3x)^3} \)

Simplify the equation:

\(\displaystyle 1.6 = \frac{4x^2}{(1 – x)(2 – 3x)^3} \)

Solving this cubic equation is complex and typically requires numerical methods. For competitive exams, a simplified assumption might be provided to estimate (x), or it could be solved graphically or using iterative methods. Here, assume (\(\displaystyle x \approx 0.2\)) for a simpler approximation.

Substitute (x = 0.2) back to check:

\(\displaystyle [\text{N}_2] \approx 1 – 0.2 = 0.8 \, \text{M} \)
\(\displaystyle [\text{H}_2] \approx 2 – 3 \times 0.2 = 1.4 \, \text{M} \)
\(\displaystyle [\text{NH}_3] \approx 2 \times 0.2 = 0.4 \, \text{M} \)

Therefore, the equilibrium concentrations are approximately:

\(\displaystyle [\text{N}_2] \approx 0.8 \, \text{M} \)
\(\displaystyle [\text{H}_2] \approx 1.4 \, \text{M} \)
\(\displaystyle [\text{NH}_3] \approx 0.4 \, \text{M} \)

Problem 4: A uniform beam of length 5 m and mass 10 kg is pivoted at one end. A 20 kg weight is placed 3 m from the pivot. Calculate the reaction force at the pivot when the system is in static equilibrium.

Solution: In static equilibrium, the sum of torques around the pivot must be zero. Let the pivot be at point A. The weight of the beam acts at its center (2.5 m from the pivot), and the 20 kg weight acts 3 m from the pivot.

The torque due to the weight of the beam:

\(\displaystyle \tau_{\text{beam}} = (10 \, \text{kg} \times 9.8 \, \text{m/s}^2) \times 2.5 \, \text{m} \)
\(\displaystyle \tau_{\text{beam}} = 98 \, \text{N} \times 2.5 \, \text{m} \)
\(\displaystyle \tau_{\text{beam}} = 245 \, \text{Nm} \)

The torque due to the 20 kg weight:

\(\displaystyle\tau_{\text{weight}} = (20 \, \text{kg} \times 9.8 \, \text{m/s}^2) \times 3 \, \text{m} \)
\(\displaystyle \tau_{\text{weight}} = 196 \, \text{N} \times 3 \, \text{m} \)
\(\displaystyle \tau_{\text{weight}} = 588 \, \text{Nm} \)

The sum of torques must be zero for static equilibrium:

\(\displaystyle \tau_{\text{beam}} + \tau_{\text{weight}} = \tau_{\text{reaction}} \)
\(\displaystyle 245 + 588 = \tau_{\text{reaction}} \)
\(\displaystyle \tau_{\text{reaction}} = 833 \, \text{Nm} \)

The reaction force at the pivot must balance the torques:

\(\displaystyle F_{\text{reaction}} = \frac{\tau_{\text{reaction}}}{L} = \frac{833 \, \text{Nm}}{5 \, \text{m}} \)
\(\displaystyle F_{\text{reaction}} = 166.6 \, \text{N} \)

Therefore, the reaction force at the pivot is (\(\displaystyle 166.6 \, \text{N}\)).

Problem 5: A car is moving at a constant speed of 60 km/h on a straight road. The drag force acting on the car is (\(\displaystyle 400 \, \text{N}\)). Calculate the power required to maintain this speed.

Solution: Power (P) required to maintain a constant speed against a force (drag force) is given by:

\(\displaystyle P = F \times v \)

Given: Drag force, F = 400 N; Speed, (\(\displaystyle v = 60 \, \text{km/h} = 60 \times \frac{1000}{3600} \, \text{m/s} = 16.67 \, \text{m/s} \))

Calculate the power:

\(\displaystyle P = 400 \, \text{N} \times 16.67 \, \text{m/s} \)
\(\displaystyle P = 6668 \, \text{W} \)
\(\displaystyle P = 6.668 \, \text{kW} \)

Therefore, the power required to maintain a constant speed of 60 km/h is approximately (6.668 kW).

Problem 6: For the reaction (\(\displaystyle \text{H}_2(g) + \text{I}_2(g) \rightleftharpoons 2\text{HI}(g) \)), the equilibrium concentrations at a certain temperature are (\(\displaystyle [\text{H}_2] = 0.1 \, \text{M}), ([\text{I}_2] = 0.1 \, \text{M}\)), and (\(\displaystyle [\text{HI}] = 0.5 \, \text{M}\)). Calculate the equilibrium constant (K_c) for the reaction.

Solution: The equilibrium constant (K_c) is given by:

\(\displaystyle K_c = \frac{[\text{HI}]^2}{[\text{H}_2][\text{I}_2]} \)

Given:
(\(\displaystyle [\text{H}_2] = 0.1 \, \text{M}\))
(\(\displaystyle [\text{I}_2] = 0.1 \, \text{M}\))
(\(\displaystyle [\text{HI}] = 0.5 \, \text{M}\))

Calculate (K_c):

\(\displaystyle K_c = \frac{(0.5)^2}{0.1 \times 0.1} \)
\(\displaystyle K_c = \frac{0.25}{0.01} \)
\(\displaystyle K_c = 25 \)

Therefore, the equilibrium constant (K_c) for the reaction is (25).

FAQs