The 19th century was a period of remarkable scientific discovery, particularly in the field of electromagnetism. Before this era, electricity and magnetism were thought to be unrelated phenomena.
The real breakthrough came in 1820 when Ørsted, a Danish physicist, discovered that a compass needle was deflected when placed near a wire carrying an electric current. This was the first evidence that electricity could create a magnetic field.
Shortly after Ørsted’s discovery, Ampère showed that two parallel wires carrying currents attract or repel each other depending on the direction of the currents. This interaction was due to the magnetic fields created by the electric currents.
The work of Ørsted and Ampère set the stage for other scientists to further explore and eventually unify the concepts of electricity and magnetism into a single theory of electromagnetism.
Faraday made the next significant leap. He discovered electromagnetic induction, showing that a changing magnetic field could produce an electric current in a wire. This principle is the basis for generators and transformers.
Maxwell was the one who synthesized all previous discoveries into a comprehensive set of equations, now known as Maxwell’s equations. These equations describe how electric and magnetic fields are generated and altered by each other and by charges and currents. With the foundation laid by these great scientists, the concept of magnetic dipoles and the torque on current loops could be understood.
Torque
Imagine you’re trying to open a tight jar lid. The force you apply to the lid and the distance from the center of the lid where you apply this force combine to create a twisting or rotational force. This is what we call torque in physics.
Torque is a measure of the force that can cause an object to rotate about an axis. Just like a force causes an object to move, torque causes an object to spin.
The formula for torque is:
\(\displaystyle \tau = F \times r \times \sin(\theta) \)
The unit of torque is the Newton-meter (Nm). It’s a combination of the unit of force (Newtons) and the unit of distance (meters). So, if you apply a force of 1 Newton at a distance of 1 meter from the axis, you’re generating 1 Newton-meter of torque.
Think of a see-saw. If you push down on the end farthest from the pivot point, it’s easier to lift the person on the other side. That’s because you’re applying a larger torque due to the greater distance from the pivot. If you tried pushing closer to the middle, you’d have to use much more force to achieve the same effect.
Torque is crucial because it’s the key to rotation. Without torque, we wouldn’t have things like car engines, wind turbines, or even simple door handles working the way they do. It’s all about using force effectively to create rotation.
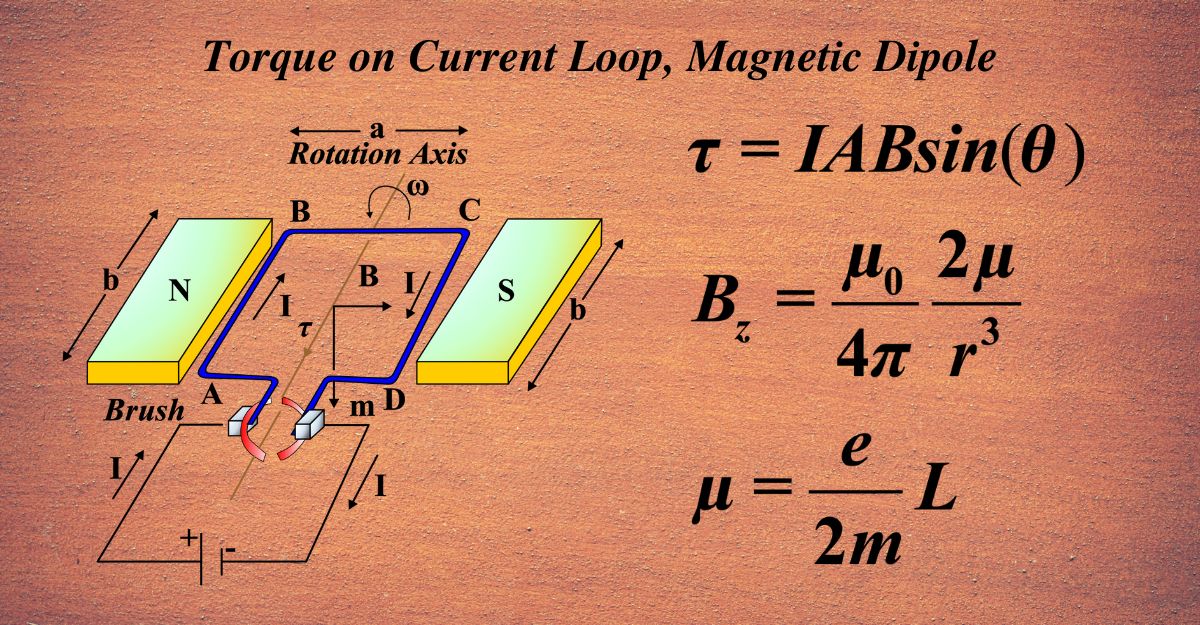
Torque on Current Loop, Magnetic Dipole
A magnetic dipole is created by a current loop. When this loop is placed in a magnetic field, it experiences a torque. This torque tends to align the dipole with the magnetic field.
Torque on Current Loop: Imagine a loop of wire through which an electric current is flowing. This loop is placed in a magnetic field, which is an invisible field around a magnet where magnetic forces are exerted.
The magnetic field interacts with the electric current in the loop. This interaction causes a force to act on the loop. This force doesn’t push the loop in any direction; instead, it causes the loop to rotate. This rotational force is what we call torque.
Magnetic Dipole: Now, let’s talk about the term magnetic dipole. It’s like a tiny bar magnet with a north and south pole, created by the current loop. Because it has two poles (di- means two), it creates a magnetic field similar to a bar magnet.
The strength of this magnetic dipole is measured by something called the magnetic dipole moment. It’s a vector that points from the south to the north pole of the dipole.
Torque on a Magnetic Dipole: When our current loop (the magnetic dipole) is in a magnetic field, it experiences torque. A rectangular loop carrying a current (I) is placed in a magnetic field (B). The loop has a length (a) and width (b), making the area (A = a×b ).
- Parallel Arms: The arms of the loop parallel to the magnetic field experience no force because the magnetic force is perpendicular to the current and the field.
- Perpendicular Arms: The arms perpendicular to the magnetic field experience a force. This force is given by (\(\displaystyle F = I \times b \times B \)) for each arm.
Even though forces (F1) and (F2) act on the perpendicular arms, they are equal and opposite, leading to no net force on the loop. However, these forces are not aligned, creating a couple that results in a torque.
The torque (τ) is the force times the distance from the axis of rotation (which is half the width of the loop, (a/2)) times the sine of the angle (θ) between the magnetic field and the normal to the loop’s plane. So, the torque on one side is (\(\displaystyle F_1 \times (a/2) \times \sin(\theta) \)), and the same for the other side.
Combining the torques from both sides, we get:
\(\displaystyle \tau = F_1 \times \frac{a}{2} \times \sin(\theta) + F_2 \times \frac{a}{2} \times \sin(\theta) \)
Since (F1 = F2 = I×b×B ), we can substitute and simplify:
\(\displaystyle \tau = I \times b \times B \times \frac{a}{2} \times \sin(\theta) + I \times b \times B \times \frac{a}{2} \times \sin(\theta) \)
\(\displaystyle \tau = 2 \times I \times b \times B \times \frac{a}{2} \times \sin(\theta) \)
\(\displaystyle \tau = I \times a \times b \times B \times \sin(\theta) \)
And since (A = a×b ), the final expression for torque is:
\(\displaystyle \tau = I \times A \times B \times \sin(\theta) \)
The torque tends to rotate the loop such that it aligns with the magnetic field. If (θ = 0) or (θ= 180) degrees, the torque is zero because the loop is already aligned with the field.
The product ( I ×A ) is known as the magnetic dipole moment (µ), which is a measure of the strength of the magnetic dipole.
Remember, the key takeaway is that the torque tries to align the current loop with the magnetic field, and this interaction is described by the torque equation involving the current, the area of the loop, the magnetic field, and the angle of alignment.
Rectangular loop carrying a steady current:
A rectangular current loop is simply a piece of wire bent into a rectangular shape with an electric current flowing through it. This loop can be characterized by its length (l) and width (b), and the current (I) that flows through it.
When a current flows through this loop, it creates a magnetic field around it. The right-hand rule can determine the direction of this magnetic field: if you point the thumb of your right hand in the direction of the current, your fingers will curl in the direction of the magnetic field lines.
This setup is important because it’s the simplest form of a magnetic dipole, a fundamental component in many electrical devices, like motors and generators. The magnetic field created by the current loop interacts with other magnetic fields, which can cause the loop to experience forces and torques.
The magnetic field created by a rectangular current loop is more complex than a circular loop because of the corners, but the basic principles are the same. The field lines form closed loops that go around the wire, and the strength of the field depends on the current and the size of the loop.
If this rectangular loop is placed in another magnetic field, such as the Earth’s magnetic field or that of a nearby magnet, it will experience a torque. This torque will try to align the loop’s magnetic field with the external field. The expression for this torque is:
\(\displaystyle \tau = I \cdot A \cdot B \cdot \sin(\theta) \)
where (τ) is the torque, (I) is the current, (A) is the area of the loop (l ×b), (B) is the external magnetic field, and (θ) is the angle between the normal to the loop and the magnetic field. The current in the loop creates a magnetic field, and when placed in an external magnetic field, the loop experiences a torque that depends on the current, the area of the loop, the external magnetic field, and the angle of alignment.
Torque On A Rectangular Current Loop In A Uniform Magnetic Field
Consider a rectangular loop of wire with width (b) and length (l), carrying a steady current (I). This loop is placed in a uniform magnetic field (B). The sides of the loop perpendicular to the magnetic field experience forces due to the interaction of the magnetic field with the current. These forces are equal in magnitude but opposite in direction, given by:
\(\displaystyle F = I \cdot b \cdot B \)
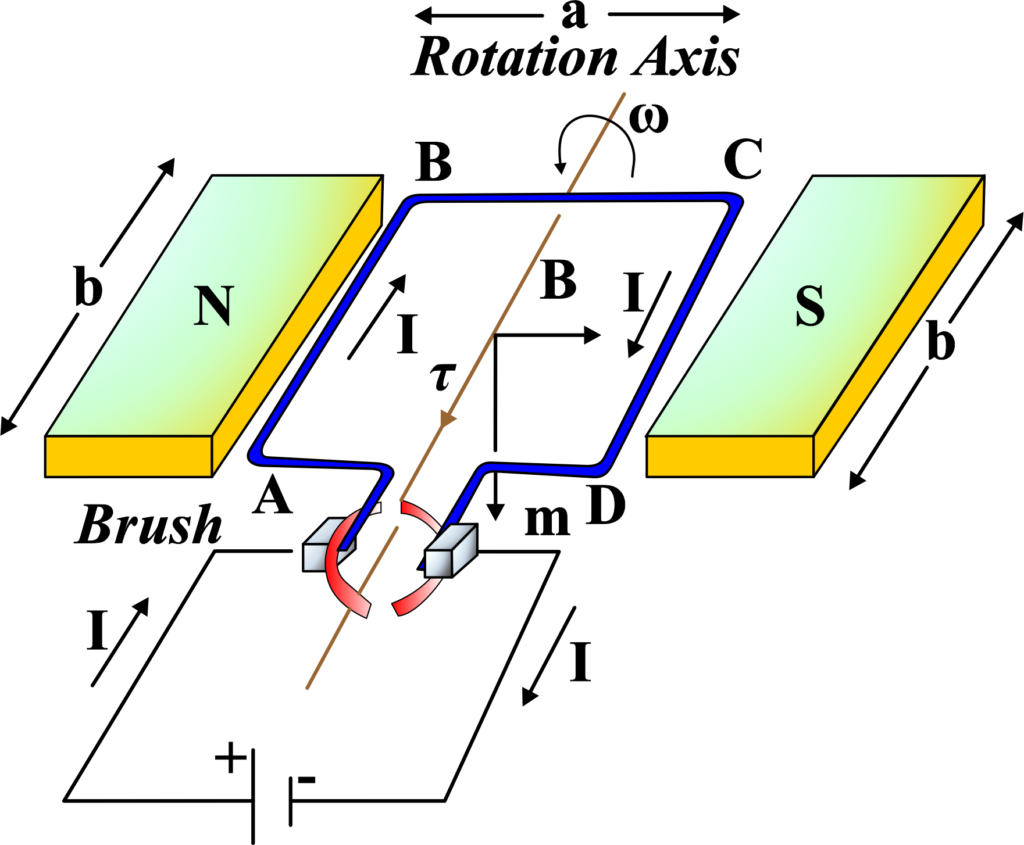
Torque (τ) is the product of force and the perpendicular distance from the axis of rotation to the line of action of the force. For one side of the loop, the torque is:
\(\displaystyle \tau_1 = F \cdot \frac{l}{2} \)
For the other side, it’s the same, so the total torque on the loop is:
\(\displaystyle \tau_{total} = 2 \cdot \tau_1 = 2 \cdot F \cdot \frac{l}{2} = F \cdot l \)
Substitute the expression for force (F) into the torque equation:
\(\displaystyle \tau_{total} = I \cdot b \cdot B \cdot l \)
The area (A) of the rectangular loop is (\(\displaystyle l \cdot b \)). So, we can write the torque as:
\(\displaystyle \tau_{total} = I \cdot A \cdot B \)
If the plane of the loop makes an angle (θ) with the magnetic field, the torque is maximized when the plane is perpendicular to the field and minimized when it’s parallel. The final expression for torque, considering the angle, is:
\(\displaystyle \tau = I \cdot A \cdot B \cdot \sin(\theta) \)
The derived expression for the torque on a rectangular current loop in a uniform magnetic field is:
\(\displaystyle \tau = I \cdot A \cdot B \cdot \sin(\theta) \)
This expression tells us that the torque depends on the current, the area of the loop, the strength of the magnetic field, and the angle at which the loop is oriented with respect to the field.
Magnetic Dipole
A magnetic dipole is like a tiny bar magnet with a north and a south pole. It’s the simplest form of a magnet that you can have. Just as a bar magnet has two poles, a magnetic dipole has two magnetic poles separated by a small distance.
A magnetic dipole can be formed by a loop of wire carrying an electric current. The current creates a magnetic field, and this field has a direction. If you use the right-hand thumb rule—where your thumb points in the direction of the current and your fingers curl in the direction of the magnetic field—you can determine the direction of the magnetic field created by the current loop.
The strength and orientation of a magnetic dipole are described by its magnetic dipole moment. This is a vector quantity, which means it has both magnitude and direction. The magnitude of the magnetic dipole moment depends on the current in the loop and the area of the loop. The formula for the magnetic dipole moment (µ) is:
\(\displaystyle \mu = I \cdot A \)
The direction of the magnetic dipole moment is given by the right-hand thumb rule. If you curl your fingers in the direction of the current, your thumb will point in the direction of the magnetic dipole moment.
Unlike electric charges, which can exist separately as positive or negative charges, magnetic poles always come in pairs—north and south. There are no magnetic monopoles. This means that magnetic field lines always form closed loops, starting from the north pole and ending at the south pole.
Circular Current Loop As A Magnetic Dipole
Let’s derive the expression for the magnetic field at a point on the axis of a circular current loop and show how it acts as a magnetic dipole. This derivation is based on the Biot-Savart Law, which describes the magnetic field generated by a current-carrying element.
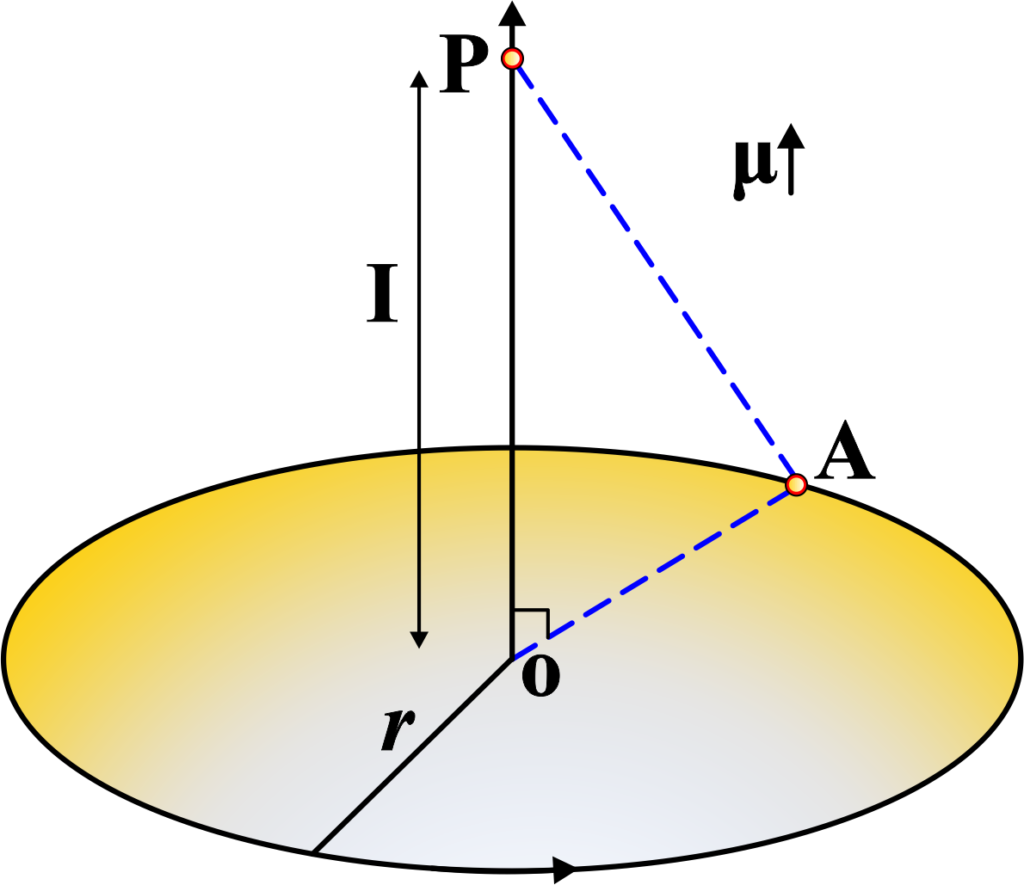
Consider a circular loop of radius (r) with a current (I) flowing through it. The loop is centered at the origin of our coordinate system, and its plane is perpendicular to the z-axis.
The Biot-Savart Law gives the magnetic field (\(\displaystyle \textbf{dB} \)) at a point in space due to a small segment of current (I) of length (\(\displaystyle\textbf{dl}\)):
$$ \textbf{dB} = \frac{\mu_0}{4\pi} \frac{I \textbf{dl} \times \hat{\textbf{r}}}{r^2} $$
where, (\(\displaystyle\hat{\textbf{r}}\)) is the unit vector from the current element to the point of interest, and (r) is the distance between them.
We want to find the magnetic field at a point (P) on the z-axis, a distance (z) from the center of the loop. Due to the symmetry of the problem, the magnetic field at (P) due to the current loop will only have a component along the z-axis, which we’ll call (Bz).
Each small segment of current (\(\displaystyle\textbf{dl}\)) contributes to (Bz). The contribution (dBz) from a small segment is:
$$ dB_z = \frac{\mu_0}{4\pi} \frac{I dl \sin(\theta)}{(r^2 + z^2)} $$
where (θ) is the angle between (\(\displaystyle\textbf{dl}\)) and (\(\displaystyle\hat{\textbf{r}}\)), which is always 90 degrees since (\(\displaystyle\textbf{dl}\)) lies in the plane of the loop and (\(\displaystyle\hat{\textbf{r}}\)) points radially outward. Therefore, (sin(θ) = 1).
To find the total magnetic field (Bz) at point (P), we integrate (dBz) over the entire loop:
\(\displaystyle B_z = \int dB_z = \frac{\mu_0}{4\pi} I \int \frac{dl}{(r^2 + z^2)} \)
Since (dl) is the circumference of the loop, (\(\displaystyle dl = 2\pi r \)), and the integral simplifies to:
\(\displaystyle B_z = \frac{\mu_0}{4\pi} \frac{I (2\pi r)}{(r^2 + z^2)} \)
Simplifying the expression for (Bz), we get:
\(\displaystyle B_z = \frac{\mu_0 I r^2}{2(r^2 + z^2)^{3/2}} \)
The magnetic dipole moment (\(\displaystyle\vec{\mu}\)) of the loop is given by:
\(\displaystyle \vec{\mu} = I \cdot A \cdot \hat{k} = I \cdot \pi r^2 \cdot \hat{k} \)
where (\(\displaystyle\hat{k}\)) is the unit vector along the z-axis.
The magnetic field (Bz) due to a magnetic dipole at a point on its axis is given by:
\(\displaystyle B_z = \frac{\mu_0}{4\pi} \frac{2 \mu}{r^3} \)
where (µ) is the magnitude of the magnetic dipole moment.
The derived expression for the magnetic field (Bz) due to a circular current loop at a point (P) on its axis shows that the loop acts as a magnetic dipole. The field decreases with the cube of the distance from the loop, similar to the electric field of an electric dipole. This derivation demonstrates the dipole nature of the magnetic field created by a circular current loop.
Magnetic dipole moment of a revolving electron
An electron revolving around a nucleus can be thought of as a tiny current loop, which gives rise to a magnetic dipole moment. Just as a current-carrying loop generates a magnetic field, so does the revolving electron. This is important in atomic and nuclear physics.
The magnetic dipole moment of a revolving electron is a measure of the magnetic effect produced by the circular motion of the electron around the nucleus. It is analogous to the electric dipole moment of two opposite charges separated by a distance.

Consider an electron of charge (–e) and mass m, revolving around a nucleus of charge +Ze in a circular orbit of radius r and velocity v, as shown in the Bohr model of the atom.
The electron can be regarded as a tiny current loop since it carries a negative charge and moves in a circular path.
The magnetic dipole moment (µ) due to the orbital motion of an electron is given by the product of the current and the area of the orbit:
\(\displaystyle \mu = I \cdot A \)
The current equivalent (I) of a revolving electron is the charge of the electron (e) divided by the time period of one revolution (T):
\(\displaystyle I = \frac{e}{T} \)
The area (A) of the electron’s orbit is the area of the circle with radius (r) (the distance of the electron from the nucleus):
\(\displaystyle A = \pi r^2 \)
By combining the expressions for current and area, we get the magnetic dipole moment due to the electron’s orbital motion:
\(\displaystyle \mu = \frac{e}{T} \cdot \pi r^2 \)
The angular momentum (L) of the electron is related to its magnetic dipole moment. The angular momentum for an electron in orbit is given by:
\(\displaystyle L = m \cdot v \cdot r \)
where (m) is the mass of the electron, (v) is its velocity, and (r) is the radius of the orbit.
The magnetic dipole moment due to the orbital motion of the electron is then proportional to its angular momentum:
\(\displaystyle \mu = \frac{e}{2m} \cdot L \)
The factor (\(\displaystyle\frac{e}{2m}\)) is known as the gyromagnetic ratio for the electron. In addition to the orbital magnetic dipole moment, electrons also have a spin magnetic dipole moment due to their intrinsic spin. This is a fundamental property of electrons, just like their charge or mass.
Also Read: The Force Between Two Parallel Current Carrying Conductor
Solved Examples
Problem 1: A rectangular loop with dimensions (\(\displaystyle 0.2 \, \text{m} \times 0.3 \, \text{m} \)) carries a current of (5 A). It is placed in a uniform magnetic field of (0.4 T) with its plane perpendicular to the magnetic field. Calculate the torque acting on the loop.
Solution: The torque (τ) on a current loop in a magnetic field is given by:
\(\displaystyle \tau = I A B \sin\theta \)
Given: (I = 5 A), (\(\displaystyle A = 0.2 \times 0.3 \, \text{m}^2 = 0.06 \, \text{m}^2 \)), (B = 0.4 T)
\(\displaystyle \tau = 5 \times 0.06 \times 0.4 \times 1 \)
\(\displaystyle \tau = 0.12 \, \text{N} \cdot \text{m} \)
The torque acting on the loop is (\(\displaystyle 0.12 \, \text{N} \cdot \text{m}\)).
Problem 2: A circular loop of radius (0.1 m) carries a current of (3A). Calculate the magnetic dipole moment of the loop.
Solution: The magnetic dipole moment (µ) of a current-carrying loop is given by:
\(\displaystyle \mu = I A \)
The area (A) of a circular loop is:
\(\displaystyle A = \pi r^2 \)
Given: (I = 3A), (r = 0.1 m)
\(\displaystyle A = \pi (0.1)^2 \)
\(\displaystyle A = 0.01 \pi \, \text{m}^2 \)
\(\displaystyle \mu = 3 \times 0.01 \pi \)
\(\displaystyle \mu = 0.03 \pi \, \text{A} \cdot \text{m}^2 \)
\(\displaystyle \mu \approx 0.0942 \, \text{A} \cdot \text{m}^2 \)
The magnetic dipole moment of the loop is approximately (\(\displaystyle 0.0942 \, \text{A} \cdot \text{m}^2 \)).
Problem 3: A circular loop of radius (0.05 m) carries a current of (2 A). It is placed in a uniform magnetic field of (0.3 T) such that the plane of the loop is parallel to the magnetic field. Calculate the torque acting on the loop.
Solution: The torque (τ) on a current loop in a magnetic field is given by:
\(\displaystyle \tau = \mu B \sin\theta \)
The magnetic dipole moment (µ) is:
\(\displaystyle \mu = I A \)
\(\displaystyle A = \pi r^2 \)
Given: (I = 2 A), (r = 0.05 m)
\(\displaystyle A = \pi (0.05)^2 \)
\(\displaystyle A = 0.0025 \pi \, \text{m}^2 \)
\(\displaystyle \mu = 2 \times 0.0025 \pi \)
\(\displaystyle \mu = 0.005 \pi \, \text{A} \cdot \text{m}^2 \)
\(\displaystyle \mu \approx 0.0157 \, \text{A} \cdot \text{m}^2\)
\(\displaystyle \tau = 0.0157 \times 0.3 \times 1 \)
\(\displaystyle \tau \approx 0.0047 \, \text{N} \cdot \text{m} \)
The torque acting on the loop is approximately (\(\displaystyle 0.0047 \, \text{N} \cdot \text{m} \)).
Problem 4: An electron revolves around a nucleus in a circular orbit of radius (\(\displaystyle 0.05 \, \text{nm}\) ) with a frequency of (\(\displaystyle 2 \times 10^{15} \, \text{Hz} \)). Calculate the magnetic dipole moment of the electron.
Solution: The magnetic dipole moment (µ ) of a revolving electron is given by:
\(\displaystyle \mu = I A \)
The current (I) is given by:
\(\displaystyle I = e f \)
(\(\displaystyle e = 1.6 \times 10^{-19} \, \text{C} \)) (charge of the electron), (f) is the frequency
The area ( A ) of the circular orbit is:
\(\displaystyle A = \pi r^2 \)
Given: (\(\displaystyle r = 0.05 \, \text{nm} = 0.05 \times 10^{-9} \, \text{m} \)), (\(\displaystyle f = 2 \times 10^{15} \, \text{Hz} \))
\(\displaystyle I = 1.6 \times 10^{-19} \times 2 \times 10^{15} \)
\(\displaystyle I = 3.2 \times 10^{-4} \, \text{A} \)
\(\displaystyle A = \pi (0.05 \times 10^{-9})^2 \)
\(\displaystyle A = \pi (2.5 \times 10^{-21}) \)
\(\displaystyle A \approx 7.85 \times 10^{-21} \, \text{m}^2 \)
\(\displaystyle \mu = 3.2 \times 10^{-4} \times 7.85 \times 10^{-21} \)
\(\displaystyle \mu \approx 2.51 \times 10^{-24} \, \text{A} \cdot \text{m}^2 \)
The magnetic dipole moment of the electron is approximately (\(\displaystyle 2.51 \times 10^{-24} \, \text{A} \cdot \text{m}^2 \)).
Problem 5: A magnetic dipole with a moment of (\(\displaystyle 1.5 \, \text{A} \cdot \text{m}^2 \)) is placed in a uniform magnetic field of (\(\displaystyle 0.2 \, \text{T} \)). The angle between the magnetic field and the dipole is (60∘). Calculate the torque acting on the dipole.
Solution: The torque (τ) on a magnetic dipole in a magnetic field is given by:
\(\displaystyle \tau = \mu B \sin\theta \)
Given: (\(\displaystyle \mu = 1.5 \, \text{A} \cdot \text{m}^2 \)), (\(\displaystyle B = 0.2 \, \text{T} \)).
\(\displaystyle \tau = 1.5 \times 0.2 \times \sin 60^\circ\)
\(\displaystyle \sin 60^\circ = \frac{\sqrt{3}}{2}\)
\(\displaystyle \tau = 1.5 \times 0.2 \times \frac{\sqrt{3}}{2} \)
\(\displaystyle \tau = 0.15 \sqrt{3} \)
\(\displaystyle \tau \approx 0.26 \, \text{N} \cdot \text{m} \)
The torque acting on the dipole is approximately (\(\displaystyle 0.26 \, \text{N} \cdot \text{m} \)).
Problem 6: A magnetic dipole with a moment of (\(\displaystyle 2 \, \text{A} \cdot \text{m}^2 \)) is placed in a uniform magnetic field of (0.3 T). Calculate the potential energy of the dipole when the angle between the magnetic field and the dipole is (45∘).
Solution: The potential energy (U) of a magnetic dipole in a magnetic field is given by:
\(\displaystyle U = -\mu B \cos\theta \)
Given: (\(\displaystyle\mu = 2 \, \text{A} \cdot \text{m}^2 \)), (\(\displaystyle B = 0.3 \, \text{T}\) ).
\(\displaystyle U = -2 \times 0.3 \times \cos 45^\circ \)
\(\displaystyle \cos 45^\circ = \frac{1}{\sqrt{2}} \)
\(\displaystyle U = -2 \times 0.3 \times \frac{1}{\sqrt{2}} \)
\(\displaystyle U = -0.6 \times \frac{1}{\sqrt{2}} \)
\(\displaystyle U = -0.6 \times 0.707 \)
\(\displaystyle U \approx -0.424 \, \text{J} \)
The potential energy of the dipole is approximately (-0.424 J).
FAQs
What is the torque on a current-carrying loop in a magnetic field?
The torque on a current-carrying loop in a magnetic field is the rotational force that acts on the loop due to the interaction between the magnetic field and the current. This torque tends to rotate the loop to align its plane perpendicular to the magnetic field lines.
How does the orientation of a current loop affect the torque experienced in a magnetic field?
The torque experienced by a current loop in a magnetic field depends on the angle between the plane of the loop and the magnetic field. The torque is maximum when the plane of the loop is parallel to the field and zero when it is perpendicular.
What is a magnetic dipole moment?
A magnetic dipole moment is a vector quantity that represents the strength and orientation of a magnetic dipole. It is a measure of the tendency of a magnetic object, like a current loop or a magnet, to align with a magnetic field.
How is the magnetic dipole moment of a current loop defined?
The magnetic dipole moment of a current loop is defined as the product of the current flowing through the loop and the area enclosed by the loop. It points perpendicular to the plane of the loop, following the right-hand rule.
What is the significance of the magnetic dipole moment in understanding magnetic materials?
The magnetic dipole moment is crucial in understanding the magnetic properties of materials. It helps explain the behavior of materials in external magnetic fields, their magnetization, and their alignment within magnetic domains in ferromagnetic materials.
How does the torque on a magnetic dipole in a uniform magnetic field manifest?
The torque on a magnetic dipole in a uniform magnetic field causes the dipole to experience a rotational force that tends to align the dipole moment with the magnetic field. This alignment minimizes the potential energy of the system.
Can a current loop or magnetic dipole experience a net force in a uniform magnetic field?
In a uniform magnetic field, a current loop or magnetic dipole experiences no net force, only a torque. The magnetic forces on opposite sides of the loop are equal in magnitude but opposite in direction, canceling each other out. However, if the field is non-uniform, a net force can act on the dipole, causing translational motion.