Total Internal Reflection

The concept of TIR has been known since ancient times, but it was not until the 17th century that significant progress was made in understanding it. The history of TIR is closely linked with the development of the wave theory of light.

People have long observed the effects of TIR, such as the sparkling of diamonds and the mirages seen on hot days. However, these phenomena were not scientifically explained as TIR until much later. In 1611, Johannes Kepler, a German mathematician and astronomer, discovered the phenomenon of TIR. He noticed that at a certain angle, light would not pass through a medium boundary but instead reflect back entirely.

The wave theory, proposed by Christiaan Huygens in the late 17th century, provided a framework for understanding light behavior, including TIR. However, it was not widely accepted until the 19th century.

Augustin-Jean Fresnel, a French engineer and physicist, made significant contributions to the wave theory of light. In 1823, he explained TIR in terms of wave theory, which added to the evidence supporting this theory of light. Fresnel’s work helped to explain why light reflects entirely at the boundary of two media under certain conditions.

Fresnel also invented the Fresnel rhomb, a device that uses TIR to modify the polarization of light. This invention further demonstrated the practical applications of TIR and the wave theory of light. Through these historical milestones, the understanding of TIR evolved from mere observation to a well-defined scientific principle. This journey reflects the broader development of optics and the gradual acceptance of the wave theory of light, which is now fundamental to modern physics and numerous technologies.

What is Total Internal Reflection?

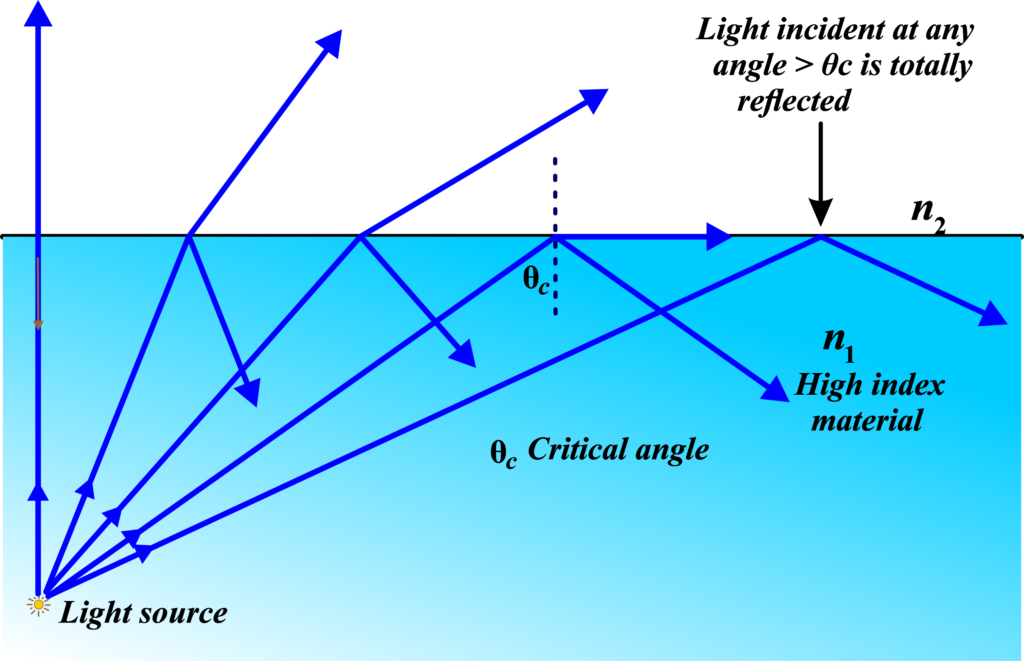
Total Internal Reflection is a phenomenon where a light ray completely reflects back into a medium from its boundary with another medium, without any refraction occurring. This happens when light travels from a denser medium to a rarer medium, like from water to air.

Total Internal Reflection is defined as the complete reflection of a light ray within a medium, such as water or glass, from the surrounding surfaces back into the medium. This means that when light tries to pass from a medium like water into the air, it doesn’t break through the surface; instead, it turns back into the water.

Imagine shining a flashlight from underwater to the surface. If you aim the flashlight directly upwards, the light passes through the water surface into the air. But if you gradually tilt the flashlight, there comes a point where no light gets out—the light is completely reflected back into the water. This is TIR in action.

A scientific example of TIR is what happens in a diamond. Diamonds have a very high refractive index, which means they can bend light significantly. When light enters a diamond, it hits the internal surfaces at such angles that it’s completely reflected within the diamond rather than passing out. This total internal reflection of light rays within the diamond causes it to sparkle brilliantly.

This principle of TIR is not just a fascinating aspect of physics but also a fundamental concept that explains why certain materials behave the way they do with light. It’s a perfect example of the laws of physics creating a visually stunning effect that we can observe in everyday life.

Conditions for Total Internal Reflection

For TIR to take place, two specific conditions must be met:

1) Transition from a Denser to a Rarer Medium

The light ray must move from a medium where it travels slower due to a higher refractive index (denser medium) to a medium where it travels faster due to a lower refractive index (rarer medium). This is like a car moving from a dirt road onto asphalt; the change in speed affects its direction.

For TIR to occur, light must move from a medium where it travels more slowly to one where it can travel faster. This is typically from a denser medium to a rarer medium. The terms ‘denser’ and ‘rarer’ refer to the optical density of the materials, not their physical weight or size.

Denser Medium: A medium is considered optically denser if it has a higher refractive index. In such a medium, light slows down. Examples of denser media include water, glass, and diamond.

Rarer Medium: A rarer medium has a lower refractive index, allowing light to speed up as it enters. Air is a common example of a rarer medium.

When light travels from a denser medium to a rarer medium, it bends away from the normal line (an imaginary line perpendicular to the boundary surface). If the angle at which the light hits the boundary (the angle of incidence) is large enough, the light won’t just bend—it will reflect back entirely into the denser medium. This is what we call Total Internal Reflection.

A practical example of this is when you look at a straw in a glass of water. Above the water, the straw appears in one location, but below the water, it seems to shift. This shift is due to the light bending as it moves from water to air. If you were to look at the straw from a very shallow angle, at some point, you would see the light reflecting off the water’s surface instead of coming out—this is TIR happening right before your eyes.

2) Incidence Angle Greater Than the Critical Angle

The angle at which the light hits the boundary (angle of incidence) must be larger than a certain limit known as the critical angle. If the angle of incidence is less than this critical angle, the light will pass through the boundary; if it’s greater, the light will reflect back into the denser medium.

For TIR to occur, the angle at which the light ray strikes the boundary of two media must be greater than a certain threshold known as the critical angle. This critical angle is specific to the pair of media involved.

Incidence Angle: This is the angle between the incoming light ray and an imaginary line called the normal, which is perpendicular to the surface at the point of contact.

Critical Angle: This is the smallest angle of incidence at which light can still undergo refraction. When the incidence angle exceeds this critical angle, refraction ceases to occur, and all the light is reflected back into the denser medium.

If you’re standing by a pool at night with a flashlight, and you shine the light towards the water at a steep angle, the light enters the water and spreads out. But as you lower the angle (making it more shallow), you’ll reach a point where the light doesn’t enter the water anymore—it all reflects off the surface and lights up the area around you instead. That point, where the light transitions from entering the water to reflecting off it, is when you’ve hit the critical angle.

When the incidence angle is greater than the critical angle, the light “decides” it cannot pass through to the less dense medium and opts to stay within the denser medium, leading to TIR. This is a natural consequence of how light behaves at the interface of two media with different optical densities.

These conditions are essential for TIR to occur. Without them, light would simply refract, or bend, as it passes from one medium to another, rather than reflecting entirely within the original medium.

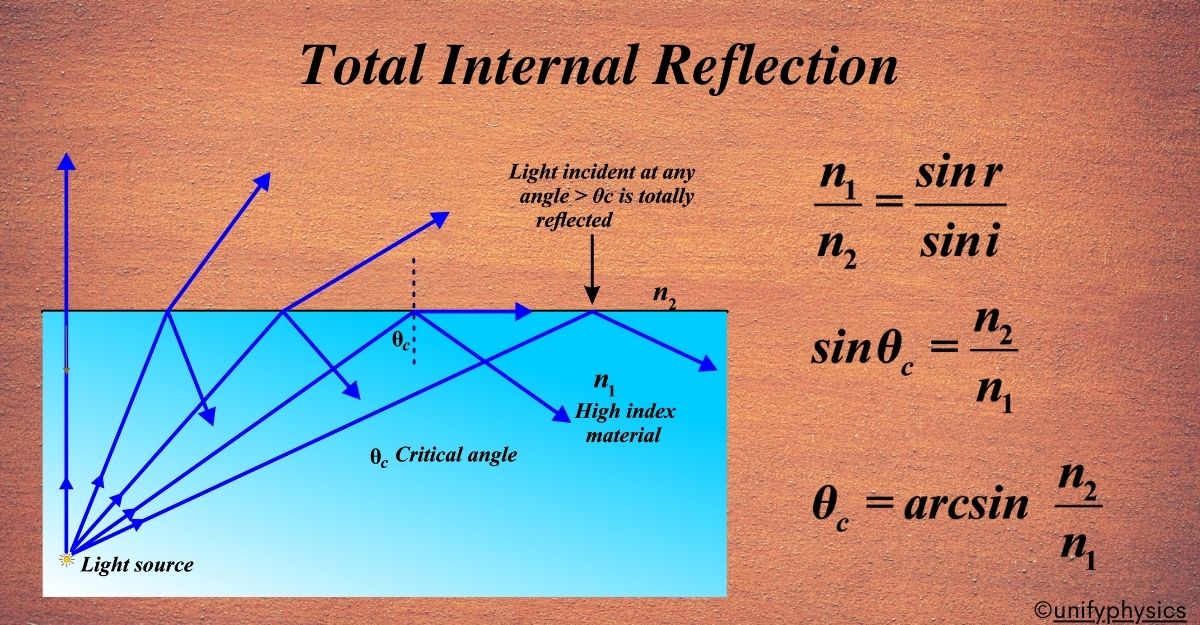
Total Internal Reflection Formula

The Total Internal Reflection (TIR) formula is a mathematical way to describe the conditions under which TIR occurs. It’s derived from Snell’s Law, which relates the angles of incidence and refraction to the refractive indices of the two media involved.

When light travels from a denser medium to a rarer medium, it bends away from the normal. If the angle of incidence is large enough, the light will not pass into the rarer medium at all; instead, it will reflect back entirely into the denser medium. This is Total Internal Reflection.

The formula for TIR can be expressed as:

\(\displaystyle\begin{equation}\label{eqn:1}\boxed{\boldsymbol{ \frac{n_1}{n_2} = \frac{\sin r}{\sin i} }} \end{equation}\)

Here, (n₁) is the refractive index of the denser medium, (n₂) is the refractive index of the rarer medium, (i) is the angle of incidence, and (r) is the angle of refraction.

In the case of TIR, the angle of refraction (r) becomes 90 degrees, which is the maximum value for (sin r). Therefore, the formula simplifies because (\(\displaystyle \sin(90^\circ) \)) is equal to 1. So, the formula becomes:

\(\displaystyle\frac{n_1}{n_2} = \frac{1}{\sin i}\)

This formula tells us that TIR happens when the sine of the angle of incidence is greater than the ratio of the refractive indices of the two media. It’s a neat equation that helps predict when TIR will occur based on the properties of the materials and the angle at which light hits the boundary between them.

Also Read: Mirror Equation

Critical Angle

The critical angle is the minimum angle of incidence above which TIR occurs. It can be calculated using the formula:

\(\displaystyle\begin{equation}\label{eqn:2}\boxed{\boldsymbol{ \sin \theta_c = \frac{n_2}{n_1} }} \end{equation}\)

where (θ_c) is the critical angle.

The critical angle is the specific angle of incidence at which the angle of refraction is exactly 90 degrees. This means that when light travels from a denser medium to a rarer medium at this angle, it refracts along the boundary, never actually leaving the denser medium.

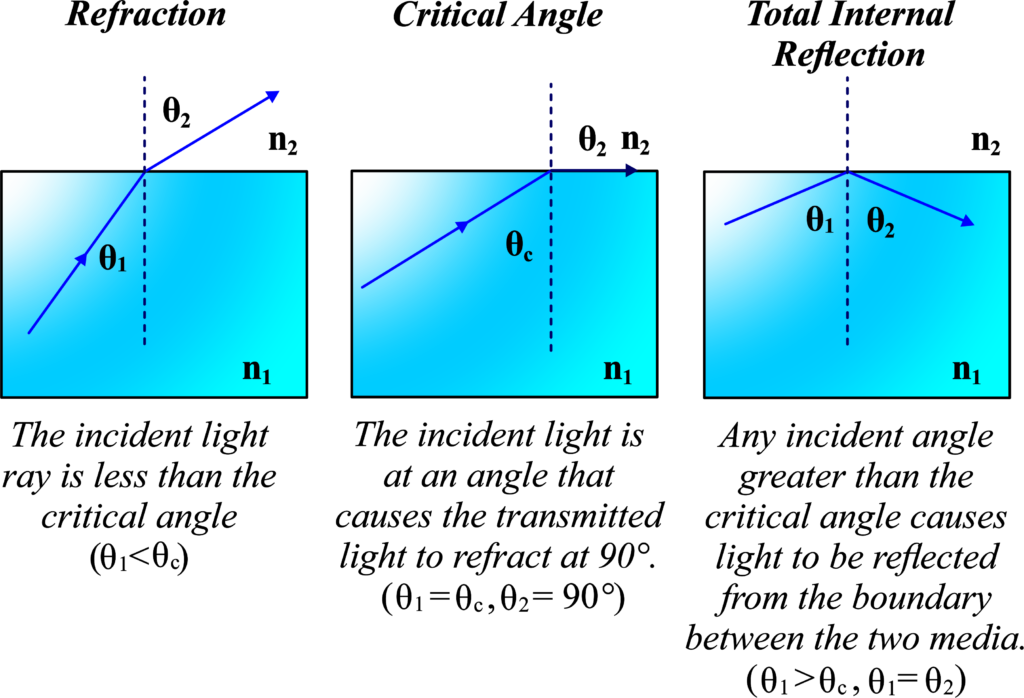
To understand this, imagine you’re holding a laser pointer inside a glass of water. If you point it straight up, the light exits the water. As you slowly tilt the laser pointer towards the side of the glass, the light starts to bend more and more upon exiting. There’s a particular angle where the light runs exactly along the surface of the water—this is the critical angle. If you tilt the laser pointer even further, the light doesn’t exit the water at all; it reflects back inside. That’s TIR happening, and it only occurs when the angle of incidence is greater than the critical angle.

The value of the critical angle depends on the combination of materials involved. For example, for the water-to-air boundary, the critical angle is approximately 48.6 degrees. This angle is unique to each pair of media because it’s determined by their refractive indices. The critical angle is the threshold angle of incidence for TIR to occur. It’s a precise value that marks the transition from refraction to total internal reflection when light moves from a denser to a rarer medium.

To derive the expression for the critical angle, we’ll start with Snell’s Law, which relates the angles and refractive indices of two different media.

Snell’s Law states that the product of the refractive index of the first medium (n₁) and the sine of the angle of incidence (θ_i) is equal to the product of the refractive index of the second medium (n₂) and the sine of the angle of refraction (θ_r).

\(\displaystyle n_1 \cdot \sin(\theta_i) = n_2 \cdot \sin(\theta_r) \)

The angle of refraction (θ_r) is 90 degrees, which means the light ray grazes along the boundary. At this angle, the sine of the angle of refraction is equal to 1.

\(\displaystyle n_1 \cdot \sin(\theta_c) = n_2 \cdot \sin(90^\circ) \)

\(\displaystyle n_1 \cdot \sin(\theta_c) = n_2 \)

We want to find the critical angle, so we rearrange the equation to solve for θc.

\(\displaystyle \sin(\theta_c) = \frac{n_2}{n_1} \)

To get the critical angle itself, we take the inverse sine (arcsin) of both sides.

\(\displaystyle\begin{equation}\label{eqn:3}\boxed{\boldsymbol{ \theta_c = \arcsin\left(\frac{n_2}{n_1}\right)}} \end{equation}\)

Here, (θ_c) is the critical angle, (n₁) is the refractive index of the denser medium, and (n₂) is the refractive index of the rarer medium. This derived expression tells us that the critical angle depends on the ratio of the refractive indices of the two media involved.

This derivation shows that the critical angle is the angle of incidence for which the refracted ray would travel along the boundary, leading to total internal reflection when the incidence angle is greater than this critical angle.

Examples of Total Internal Reflection

Optical Fibre

TIR keeps Light signals within the core of the optical fiber, allowing for high-speed data transmission over long distances. An optical fiber is a thin glass or plastic strand designed to carry light along its length. Inside the fiber, light travels through the core, which is the central part made of a denser material. Surrounding the core is the cladding, which has a lower refractive index.

When light enters the fiber, it does so at a particular angle that allows it to bounce back and forth within the core without escaping. This bouncing is due to TIR. Each time the light hits the boundary between the core and the cladding, it’s reflected back into the core if the angle of incidence is greater than the critical angle. This keeps the light trapped inside the core as it zigzags down the fiber.

The core’s material has a higher refractive index than the cladding, which means it’s optically denser. Because of this difference in refractive index, light hitting the core-cladding boundary at a shallow angle (greater than the critical angle) undergoes TIR. The light is totally internally reflected, and it continues to travel down the length of the fiber.

Imagine you’re inside a very long, straight tunnel, and you have a bouncy ball that you can throw against the walls. If you throw the ball straight ahead, it’ll just come back to you. But if you throw it at an angle towards the wall, it’ll bounce off the wall and continue down the tunnel. If you keep throwing it at the right angle, it’ll bounce from side to side all the way down the tunnel without ever coming out. That’s similar to how light behaves in an optical fiber, with the walls of the tunnel representing the core-cladding boundary where TIR occurs.

Mirage

A mirage is an optical illusion caused by TIR, where layers of air at different temperatures cause light from the sky to bend and create the appearance of water. It makes it seem like there is water on the ground when there isn’t any. This happens because of TIR.

When the ground is very hot, it heats the air above it. This hot air is less dense and has a lower refractive index than the cooler air above it. Light rays coming down from the cooler, denser air into the hot, less dense air bend (or refract) away from the normal line (an imaginary line perpendicular to the boundary between the two air layers). As the light rays keep bending, they eventually hit the boundary at an angle greater than the critical angle, which causes them to undergo TIR.

Instead of continuing to bend and reach the ground, the light rays reflect off the hot air layer and travel back up, creating the appearance of water. This is because the reflected light from the sky resembles the way light reflects off a water surface.

The scientific reason behind this is the gradient in the refractive index of the air caused by the temperature difference. The refractive index keeps decreasing as you move closer to the hot ground. This gradient causes the light rays to bend gradually until they reflect internally, creating the mirage.

Diamond

Diamonds sparkle brilliantly because of TIR, as light entering the diamond is reflected multiple times within before emerging. A diamond’s brilliance and sparkle are largely due to TIR. Diamonds have a very high refractive index, which means they can bend light significantly. When light enters a diamond, it is refracted (bent) at the first interface it encounters. As the light travels inside the diamond, it hits the internal surfaces at angles greater than the critical angle, which is quite small for diamonds due to their high refractive index.

Because the angles of incidence are greater than the critical angle, the light undergoes TIR, reflecting back and forth within the diamond. This process traps the light inside, causing it to interact with the diamond’s facets multiple times before finally emerging. The result is the characteristic sparkle that diamonds are known for.

The critical angle for diamond-air boundaries is around 24 degrees, which is much lower than for many other materials. This means that even light entering the diamond at relatively shallow angles can experience TIR. The precise cutting of diamonds into multi-faceted shapes is designed to maximize this effect, ensuring that most of the light entering a diamond will be totally internally reflected.

Applications of Total Internal Reflection

Total Internal Reflection (TIR) is not just a fascinating physical phenomenon but also has numerous practical applications that have significant impacts on our daily lives and various industries.

• Fiber Optics: One of the most important applications of TIR is in fiber optics. Optical fibers are thin strands of glass or plastic that use TIR to transmit light over long distances. Inside these fibers, light bounces back and forth without escaping, allowing for the transmission of data in telecommunications and internet connections.
• Medical Endoscopes: TIR is used in medical endoscopes, which are devices that allow doctors to look inside the human body. The light travels through the optical fibers in the endoscope, reflecting internally to illuminate and visualize internal organs without invasive surgery.
• Periscopes: Used in submarines and other areas where direct line-of-sight observation is not possible, periscopes use prisms to reflect images through a tube, allowing one to see over or around obstacles. TIR ensures that the image transmitted is bright and clear.
• Binoculars and Telescopes: Many optical devices, such as binoculars and telescopes, use prisms that rely on TIR to reflect and rotate images for better viewing. The prisms can turn the image right-side-up or extend the path of light to allow for more compact designs.
• Reflectors and Road Safety: Reflectors on roads, often called cat’s eyes, use TIR to reflect the headlights of vehicles back to the driver’s eyes, making lanes and road edges visible at night. This application of TIR significantly enhances road safety.
• Cameras: Single-lens reflex (SLR) cameras use a pentaprism that relies on TIR to reflect light from the lens up to the viewfinder. This allows photographers to see exactly what the lens is capturing.

These applications show how TIR is integral to many technologies that we rely on every day. From internet communications to medical diagnostics and road safety, the principles of TIR are being utilized to make our lives easier and safer.

Facts of Total Internal Reflection

Total Internal Reflection (TIR) is a phenomenon that has some intriguing facts associated with it.

• Occurs at the Boundary: TIR happens when light reaches the boundary between two different media, specifically from a denser medium to a rarer medium.
• No Light Escapes: During TIR, all the light is reflected back into the denser medium. Unlike regular reflection, there is no transmission of light into the rarer medium.
• Depends on Refractive Index: The occurrence of TIR is dependent on the refractive indices of the two media involved. The greater the difference in refractive indices, the more likely TIR is to occur.
• Critical Angle is Key: The critical angle is the minimum angle of incidence for which TIR occurs. It varies depending on the media involved and is always less than 90 degrees.
• Efficiency: TIR is highly efficient because there is no loss of light through transmission. This makes it ideal for applications where light needs to be contained, such as in fiber optics.
• Temperature Affects Critical Angle: The critical angle can change with temperature because it affects the refractive index of the media. Generally, as the temperature increases, the critical angle also increases.
• Used in Nature and Technology: TIR is not just a laboratory phenomenon; it occurs in nature, like in mirages, and is used in various technologies, from medical devices to communication systems.

Solved Examples

Example 1: Calculate the critical angle for the interface between diamond (refractive index = 2.42) and air (refractive index = 1.0).

Solution: The critical angle (θ_c) is given by:

\(\displaystyle\sin \theta_c = \frac{n_2}{n_1}\)

Given: n₁ = 2.42 (diamond); n₂ = 1.0 (air)

Substitute the values:

\(\displaystyle\sin \theta_c = \frac{1.0}{2.42} \approx 0.4132\)

Now find (θ_c):

\(\displaystyle\theta_c = \sin^{-1}(0.4132) \approx 24.41^\circ\)

The critical angle for the interface between diamond and air is approximately 24.41°.

Example 2: A light ray travels from glass (refractive index = 1.5) to water (refractive index = 1.33). Determine the minimum angle of incidence for total internal reflection to occur.

Solution: Total internal reflection occurs when the angle of incidence is greater than the critical angle. The critical angle (θ_c) is given by:

\(\displaystyle\sin \theta_c = \frac{n_2}{n_1}\)

Given: n₁ = 1.5 (glass); n₂ = 1.33 (water)

Substitute the values:

\(\displaystyle\sin \theta_c = \frac{1.33}{1.5} \approx 0.8867\)

Now find (θ_c):

\(\displaystyle\theta_c = \sin^{-1}(0.8867) \approx 62.46^\circ\)

The minimum angle of incidence for total internal reflection to occur when traveling from glass to water is approximately 62.46°.

Example 3: A light ray travels from water (refractive index = 1.33) into glass (refractive index = 1.5). If the angle of incidence in water is 50°, determine if total internal reflection occurs. If not, calculate the angle of refraction in the glass.

Solution: First, determine if total internal reflection occurs by comparing the angle of incidence to the critical angle. The critical angle (θ_c) is given by:

\(\displaystyle\sin \theta_c = \frac{n_2}{n_1}\)

Given: n₁ = 1.33 (water) ; n₂ = 1.5 (glass)

Substitute the values:

\(\displaystyle\sin \theta_c = \frac{1.33}{1.5} \approx 0.8867\)

Now find (θ_c):

\(\displaystyle\theta_c = \sin^{-1}(0.8867) \approx 62.46^\circ\)

Since the angle of incidence (50°) is less than the critical angle (62.46°), total internal reflection does not occur. Next, use Snell’s Law to find the angle of refraction (θ₂):

\(\displaystyle n_1 \sin \theta_1 = n_2 \sin \theta_2\)

Substitute the values:

\(\displaystyle 1.33 \sin 50^\circ = 1.5 \sin \theta_2\)

Since (\(\displaystyle\sin 50^\circ \approx 0.766\)):

\(\displaystyle 1.33 \times 0.766 = 1.5 \sin \theta_2\)
\(\displaystyle 1.018 \approx 1.5 \sin \theta_2\)
\(\displaystyle\sin \theta_2 = \frac{1.018}{1.5} \approx 0.6787\)

Now find (θ₂):

\(\displaystyle\theta_2 = \sin^{-1}(0.6787) \approx 42.65^\circ\)

Total internal reflection does not occur. The angle of refraction in the glass is approximately 42.65°.

Example 4: A light ray is incident on one face of an equilateral glass prism (refractive index = 1.52) at an angle of 45°. Calculate the angle of refraction inside the prism and determine if total internal reflection occurs at the second face.

Solution: First, use Snell’s Law to find the angle of refraction ((\theta_2)) inside the prism:

\(\displaystyle n_1 \sin \theta_1 = n_2 \sin \theta_2\)

Given: n₁ = 1.0 (air); n₂ = 1.52 (glass); \(\displaystyle\theta_1 = 45^\circ \)

Substitute the values:

\(\displaystyle 1.0 \sin 45^\circ = 1.52 \sin \theta_2\)

Since (\sin 45^\circ = 0.7071):

\(\displaystyle 0.7071 = 1.52 \sin \theta_2\)
\(\displaystyle\sin \theta_2 = \frac{0.7071}{1.52} \approx 0.4652\)

Now find (θ₂):

\(\displaystyle\theta_2 = \sin^{-1}(0.4652) \approx 27.78^\circ\)

Since the prism is equilateral, the angle of incidence at the second face is:

\(\displaystyle 60^\circ – 27.78^\circ = 32.22^\circ\)

To check for total internal reflection at the second face, calculate the critical angle (θ_c):

\(\displaystyle\sin \theta_c = \frac{1.0}{1.52} \approx 0.6579\)
\(\displaystyle\theta_c = \sin^{-1}(0.6579) \approx 41.14^\circ\)

Since the angle of incidence (32.22°) is less than the critical angle (41.14°), total internal reflection does not occur. The angle of refraction inside the prism is approximately 27.78°, and total internal reflection does not occur at the second face.

Example 5: A light pipe uses total internal reflection to guide light. If the light pipe is made of a material with a refractive index of 1.6 and is surrounded by air, calculate the maximum angle of incidence inside the pipe for which total internal reflection occurs.

Solution: Total internal reflection occurs when the angle of incidence is greater than the critical angle. The critical angle (θ_c) is given by:

\(\displaystyle\sin \theta_c = \frac{n_2}{n_1}\)

Given: n₁ = 1.6 (light pipe material); n₂ = 1.0 (air)

Substitute the values:

\(\displaystyle\sin \theta_c = \frac{1.0}{1.6} = 0.625\)

Now find (θ_c):

\(\displaystyle\theta_c = \sin^{-1}(0.625) \approx 38.68^\circ\)

Since we need the maximum angle of incidence inside the pipe, we take the complementary angle to the critical angle:

\(\displaystyle\theta_{\text{max}} = 90^\circ – \theta_c = 90^\circ – 38.68^\circ \approx 51.32^\circ\)

The maximum angle of incidence inside the light pipe for total internal reflection to occur is approximately 51.32°.

FAQs