Types of Semiconductors

The journey of semiconductors began in the early 19th century when their unique properties were first observed. However, it wasn’t until the 20th century that semiconductors found their place in the heart of electronic devices.

Initially, semiconductors were just curious materials that didn’t fit neatly into the categories of conductors or insulators. Their conductivity seemed to increase with temperature, which was opposite to the behavior of metals. The first practical use of semiconductors in electronics was the cat’s-whisker detector in 1904. This was a type of diode and an essential component in early radio receivers¹.

The real breakthrough came with the invention of the transistor in 1947 by Bardeen and Brattain at Bell Laboratories, followed by Shockley’s invention of the junction transistor in 1948. This marked the beginning of the transistor era, leading to the miniaturization and efficiency of electronic devices.

In 1958, the integrated circuit was invented, which allowed multiple electronic components to be fabricated on a single piece of semiconductor material. This innovation paved the way for modern electronics, computers, and the digital age.

Silicon quickly became the most widely used semiconductor material due to its abundance and favorable electronic properties. Later, other materials like germanium and gallium arsenide were explored for different applications.

The process of doping—adding impurities to the semiconductor—created two main types of semiconductors:

• N-type: Where the material has an excess of electrons.
• P-type: Where the material has an excess of holes (positive charge carriers).

These doped semiconductors are known as extrinsic semiconductors, and they are fundamental to creating semiconductor junctions, which are the building blocks of diodes, transistors, and all semiconductor devices.

Today, we’re looking at even more advanced semiconductor types with structures like SOI (Silicon On Insulator) and multigate devices, which continue to push the boundaries of what’s possible in electronics and computing.

Electrons and Holes in Semiconductors

In the world of semiconductors, we deal with materials that are not quite conductors and not quite insulators. They have a unique place in the electrical conductivity spectrum because of their ability to conduct electricity under certain conditions. This behavior is largely due to the presence of electrons and holes.

Electrons in Semiconductors: Electrons are subatomic particles with a negative charge, found in all atoms. In conductors, these electrons are free to move about, which is why metals conduct electricity so well. In semiconductors, however, electrons can move only if they have enough energy to jump from the valence band (where they are bound to atoms) to the conduction band (where they are free to move).

When an electron gains enough energy (for example, from heat or light), it can leap into the conduction band, leaving behind a vacancy in the valence band. This vacancy is what we call a hole.

Holes in Semiconductors: A hole is essentially the absence of an electron in the valence band. It’s a bit like an empty seat in a crowded theater—if someone gets up and moves to a different spot, they leave an empty seat behind. In a semiconductor, when an electron moves, it leaves behind a hole that can also move as neighboring electrons jump in to fill it.

This movement of holes is akin to a positive charge moving through the material, which is why we can think of holes as positive charge carriers. When an electric field is applied to a semiconductor, both electrons and holes contribute to the flow of current.

When we talk about current in semiconductors, we’re talking about the movement of both electrons and holes. They move in opposite directions when an electric field is applied:

• Electrons move toward the positive side because they are negatively charged.
• Holes move toward the negative side because they behave like positive charges.

This dance between electrons and holes is what allows semiconductors to conduct electricity and is the fundamental principle behind semiconductor devices like diodes and transistors.

Electron recombines with a hole:

When an electron recombines with a hole in a semiconductor, it’s a process where the electron falls from the conduction band to fill the vacancy in the valence band that the hole represents. This recombination results in the annihilation of both the electron and the hole. There are two main types of recombination:

Radiative Recombination: In radiative recombination, the electron transitions directly from the conduction band to the valence band and releases energy in the form of a photon. This is the principle behind light-emitting diodes (LEDs) and laser diodes, where the emitted light is a direct result of electron-hole recombination.

Non-Radiative Recombination: Non-radiative recombination does not emit photons; instead, the energy is released as heat or vibrations in the crystal lattice, known as phonons. This type of recombination can occur through different mechanisms, such as defect-mediated recombination or Auger recombination, where the energy is transferred to another electron or hole, which then dissipates it as heat.

The recombination of electrons and holes is a fundamental process in semiconductors, affecting their electrical and optical properties. It plays a crucial role in the operation of various semiconductor devices, from solar cells to transistors.

Mobility of Electrons and Holes

Mobility is a measure of how quickly charge carriers (which can be electrons or holes) can move through a semiconductor when an electric field is applied. It’s like measuring how fast a person can walk when the wind is pushing them along.

Electrons: In semiconductors, electrons are negatively charged particles that can move freely in the conduction band. Their mobility is affected by how easily they can navigate through the crystal lattice of the semiconductor. If the lattice has many impurities or defects, it’s like a path with lots of obstacles, and the electrons can’t move as quickly.

Holes: Holes are the positive charge carriers in a semiconductor. They are essentially the absence of an electron in the valence band. When an electron leaves its place in the lattice, it creates a hole that can move around just like an electron. The mobility of holes is typically less than that of electrons because the holes are moving in a more crowded environment—the valence band.

Temperature plays a significant role in mobility. As the temperature increases, the semiconductor’s atoms vibrate more. This increased vibration can scatter the charge carriers, making it harder for them to move through the material. It’s like trying to walk faster in a crowd that’s also moving.

The mobility of electrons and holes is crucial because it determines how well the semiconductor will conduct electricity. High mobility means that charge carriers can respond quickly to electric fields, which is important for the performance of electronic devices like transistors and solar cells.

Electron Mobility (µ_n): Electron mobility is a measure of how quickly an electron can move through a semiconductor when an electric field is applied.

• Electric Field (E): This is what causes the electrons to move. It’s like a slope on which the electrons can slide down.
• Force (F): When an electric field is applied, a force is exerted on the electrons. According to Newton’s second law, ( F = ma ), where ( m ) is mass and ( a ) is acceleration.
• Charge of an Electron (e): This is a fundamental property of electrons that determines how they interact with the electric field.

Now, the force exerted on an electron in an electric field is given by:

\(\displaystyle F = eE \)

This force causes the electron to accelerate. However, in a semiconductor, the electrons frequently collide with impurities and lattice vibrations, which hinders their acceleration. This leads to a concept called the average time between collisions (τ), which is the average time an electron travels before it hits something and scatters.

The acceleration can be given as:

\(\displaystyle a = \frac{F}{m} \)

But since we’re considering the average effect over many collisions, we use the effective mass (m*) of the electron, which accounts for the interaction of the electron with the crystal lattice. So, the equation becomes:

\(\displaystyle a = \frac{eE}{m^*} \)

Now, the average velocity an electron reaches due to this acceleration before it collides is called the drift velocity (v_d). Since (v_d = a τ), we can write:

\(\displaystyle v_d = \frac{eE}{m^*} \tau \)

Electron mobility is defined as the drift velocity per unit electric field, so:

\(\displaystyle \mu_n = \frac{v_d}{E} \)

Substituting the expression for (v_d) into the mobility equation, we get:

\(\displaystyle \mu_n = \frac{e \tau}{m^*} \)

And there you have it! The expression for electron mobility (µ_n) shows that it depends on the charge of the electron, the average time between collisions, and the effective mass of the electron in the semiconductor. This expression helps us understand why some materials make better semiconductors than others: if the electrons can move easily (high mobility), the material will be more conductive.

Fermi Level in Semiconductors

The Fermi level is the energy level at which the probability of finding an electron is 50%. It’s crucial to understand how semiconductors behave.

In simple terms, the Fermi Level is like the water level in a tank. It represents the highest energy level that electrons can occupy at absolute zero temperature (−273.15 °C) in a semiconductor. At this temperature, electrons fill up the energy states up to a certain point—this point is the Fermi Level.

The Fermi Level is important because it tells us about the electrical properties of a material. In a semiconductor:

• If the Fermi Level is closer to the conduction band (where electrons can move freely), it’s easier for electrons to jump up from the valence band (where they are usually stuck) and conduct electricity.
• If the Fermi Level is closer to the valence band, it’s harder for electrons to make that jump and become free to conduct electricity.

While the Fermi Level is defined at absolute zero, it also affects how the semiconductor behaves at higher temperatures. As the temperature increases, electrons gain energy and can move to higher energy levels, which changes the way electricity flows through the material.

Think of the Fermi Level as a marker of electron energy in a semiconductor. It’s not about the actual movement of electrons, but rather about their potential to move. Knowing where the Fermi Level lies helps predict how the semiconductor will conduct electricity and respond to changes like temperature or impurities.

Expression for Position of the Fermi Level

To derive the expression for the position of the Fermi Level in a semiconductor, we’ll start with some basic principles and work our way to the formula. The Fermi Level, denoted as (E_F), is the energy level at which the probability of finding an electron is 50% at absolute zero temperature.

Fermi-Dirac Distribution: At absolute zero, all the energy states below the Fermi Level are filled, and all the states above are empty. The Fermi-Dirac distribution function, which gives the probability of an energy state being occupied by an electron, is given by:

\(\displaystyle f(E) = \frac{1}{1 + e^{\frac{E – E_F}{k_B T}}} \)

• f(E) is the probability of an energy state at energy ( E ) being occupied.
• (E) is the energy of the state.
• (E_F) is the Fermi Level.
• (k_B) is Boltzmann’s constant.
• (T) is the temperature in Kelvin.

At Absolute Zero: At ( T = 0 ) K, the distribution function simplifies because any energy state (E) higher than (E_F) will have a probability of 0, and any state with (E) lower than (E_F) will have a probability of 1.

Intrinsic Semiconductors: For intrinsic (pure) semiconductors at absolute zero, the Fermi Level lies exactly in the middle of the band gap, which is the energy difference between the valence band and the conduction band.

Deriving (E_F): The position of the Fermi Level in an intrinsic semiconductor can be approximated at room temperature by considering the intrinsic carrier concentration (n_i), which is the number of free electrons or holes in the semiconductor. The expression for (n_i) is:

\(\displaystyle n_i = \sqrt{N_c N_v} e^{-\frac{E_g}{2k_B T}} \)

(N_c) and (N_v) is the effective density of states in the conduction and valence bands, respectively. (E_g) is the band gap energy.

The intrinsic carrier concentration is also related to the Fermi Level by the equation:

\(\displaystyle n_i = N_c e^{-\frac{E_c – E_F}{k_B T}} \)

where (E_c) is the energy of the conduction band minimum.

By equating the two expressions for (n_i) and solving for (E_F), we get:

\(\displaystyle E_F = E_c – k_B T \ln\left(\frac{N_c}{n_i}\right) \)

And since (n_i) is also equal to (\(\displaystyle N_v e^{-\frac{E_F – E_v}{k_B T}} \)), where (E_v) is the energy of the valence band maximum, we can also write:

\(\displaystyle E_F = E_v + k_B T \ln\left(\frac{n_i}{N_v}\right) \)

Combining these two expressions and considering that (E_F) is approximately in the middle of the band gap for intrinsic semiconductors, we can find the position of the Fermi Level relative to the band edges. This derivation shows how the Fermi Level is positioned based on the intrinsic properties of the semiconductor and its temperature.

The Lattice Bond Theory, often referred to as the Band Theory, is a fundamental concept in semiconductor physics. It explains how atoms bond in a solid and how this affects the material’s electrical properties.

Lattice Bond Theory of the Semiconductor

Atomic Bonds in Solids: In a semiconductor, atoms are arranged in a regular, repeating pattern called a lattice. Each atom forms bonds with its neighbors using its outermost electrons, also known as valence electrons.

Energy Bands: Because of the proximity of atoms in a solid, the energy levels of their valence electrons can’t be distinct. Instead, they merge to form bands:

Valence Band: This is the energy band formed by the valence electrons. It’s completely filled with electrons at an absolute zero temperature.

Conduction Band: This is the higher energy band that is empty at absolute zero but can be occupied by electrons at higher temperatures or when external energy is provided.

Band Gap: Between the valence band and the conduction band, there’s an energy gap known as the band gap. Electrons need to gain energy equal to or greater than this band gap to jump from the valence band to the conduction band and contribute to electrical conduction.

Deriving the Band Gap Expression: The band gap energy (E_g) can be expressed in terms of the potential energy between two atoms and the distance between them. However, the exact derivation involves quantum mechanics and is beyond the scope of high school physics. But we can understand it conceptually:

When two atoms come close together, their potential energy changes due to the interaction between their electrons and nuclei. The potential energy as a function of the distance between two atoms has a minimum value when the atoms are at an equilibrium distance, forming a stable bond.

If we provide enough energy to overcome this potential energy (the band gap energy), the electron can break free from the bond and move to the conduction band.

Covalent Bonds and Electron Movement: In semiconductors like silicon, each atom shares its valence electrons with four neighboring atoms, forming covalent bonds. When energy is provided (like heat or light), some electrons gain enough energy to break free from these bonds and move to the conduction band, leaving behind holes in the valence band.

Effective Mass: As electrons move through the lattice, they are affected by the periodic potential of the lattice. This gives them an effective mass (( m^* )), which is different from the free electron mass. The effective mass is a key parameter in the band theory and affects the mobility of the charge carriers.

Types of Semiconductors

Semiconductors are materials that have a conductivity between conductors and insulators, which can be modified by doping or external factors. Semiconductors are widely used in electronic devices, such as diodes, transistors, and integrated circuits.

There are two main types of semiconductors: intrinsic and extrinsic. Intrinsic semiconductors are pure semiconductors without any significant impurities or dopants. They have equal numbers of electrons and holes, which are the charge carriers that contribute to the electric current.

Extrinsic semiconductors are semiconductors that have been doped with impurities that either donate or accept electrons, creating an excess of either electrons (n-type) or holes (p-type). Extrinsic semiconductors have higher conductivity than intrinsic semiconductors.

Intrinsic Semiconductors

In intrinsic semiconductors, such as pure silicon, the crystal lattice structure plays a critical role in determining the material’s electrical properties. An intrinsic semiconductor is a pure semiconductor material with no intentional doping, meaning it does not contain any added impurities to modify its electrical properties. In an intrinsic semiconductor, the electrical conduction is primarily determined by the inherent properties of the semiconductor material itself, without the influence of external factors such as impurities or temperature.

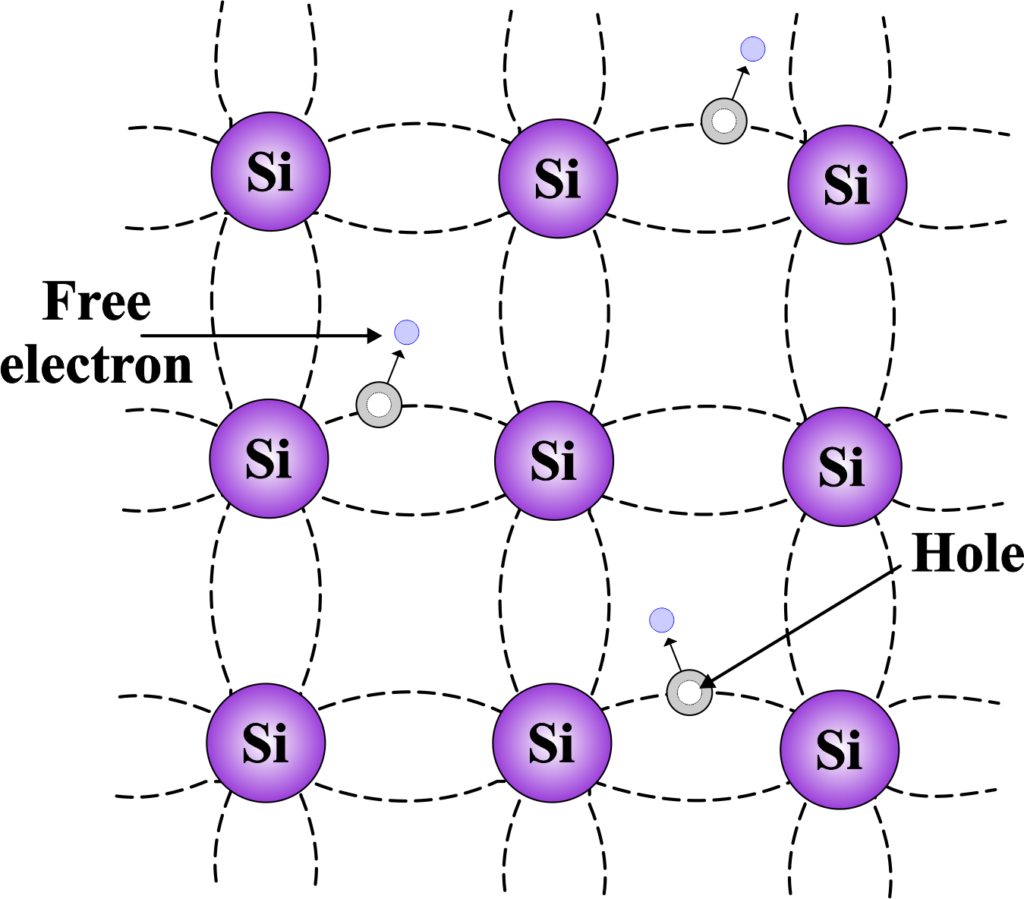
Silicon (Si) has a crystalline structure in which each silicon atom forms four covalent bonds with its neighboring silicon atoms, resulting in a tetrahedral arrangement. This gives rise to a three-dimensional crystal lattice.

The electrons in a silicon crystal are arranged in energy bands. The valence band is the band of energy levels where electrons are typically found in their normal, non-excited state. The conduction band is the higher energy band where electrons can move freely when excited.

Intrinsic semiconductors like silicon have a specific energy gap, known as the band gap, between the valence and conduction bands. For silicon, the band gap is around 1.1 electron volts (eV).

The electronic configuration of silicon is (1s² 2s² 2p⁶ 3s² 3p²). The outermost shell (valence shell) has 4 electrons, and these are the ones primarily involved in covalent bonding. Even at absolute zero temperature, some electrons in the valence band can gain energy through thermal excitation and move to the conduction band, leaving behind holes (vacant electron positions) in the valence band. This process creates electron-hole pairs.

\(\displaystyle n_{e}=n_{h}=n_{i}\)

\(\displaystyle\ n_{e} n_{h}=n_{i}^{2}\)

Where, n_e= electron density ; n_h= holre density ; n_i=intricsic carrier density

The intrinsic carrier concentration increases with temperature, as higher temperatures provide more thermal energy for electrons to move to the conduction band. In intrinsic semiconductors, the concentration of electrons in the conduction band is equal to the concentration of holes in the valence band. Intrinsic semiconductors have limited electrical conductivity at room temperature due to the relatively small number of thermally generated electron-hole pairs.

Intrinsic Carrier Concentration (n_i)

Intrinsic carrier concentration refers to the number of charge carriers (electrons and holes) in a pure semiconductor without any doping. At thermal equilibrium, the number of electrons (n) is equal to the number of holes (p), and this common value is the intrinsic carrier concentration (n_i).

• The density of States: The density of states in the conduction band (N_C) and the valence band (N_V) tells us how many states are available for electrons and holes to occupy at a given energy level.
• Maxwell-Boltzmann Approximation: At energies close to the edges of the conduction and valence bands, we can use the Maxwell-Boltzmann statistics to approximate the probability that a state at a certain energy will be occupied by an electron or hole.
• Effective Mass: Electrons and holes have an effective mass (m_e) and (m_h) that differs from their actual mass due to interactions with the lattice.
• Boltzmann’s Constant and Temperature: Boltzmann’s constant (k) and the absolute temperature (T) of the semiconductor play a role in the distribution of electrons and holes.
• Band Gap Energy: The band gap energy (E_g) is the energy difference between the conduction band and the valence band.

Using these concepts, the intrinsic carrier concentration is given by the product of the square root of the density of states for electrons and holes, multiplied by the exponential of the negative band gap energy divided by twice the product of Boltzmann’s constant and the temperature:

\(\displaystyle n_i = \sqrt{N_C N_V} e^{-\frac{E_g}{2kT}} \)

This expression tells us that the intrinsic carrier concentration depends on the temperature and the material’s band gap energy. As the temperature increases, or as the band gap energy decreases, (n_i) increases, meaning there are more charge carriers available for conduction.

Conductivity of Intrinsic Semiconductors (σ)

Electrical conductivity (σ) is a measure of a material’s ability to conduct electric current. In the case of intrinsic semiconductors, this conductivity comes from two types of charge carriers: free electrons and holes.

In intrinsic semiconductors, the number of free electrons (n) is equal to the number of holes (p), and both are equal to the intrinsic carrier concentration (n_i). The charge of an electron (e) is a fundamental constant.

The mobility of electrons (µ_n) and holes (µ_p) indicates how easily they can move through the semiconductor when an electric field is applied. The current density (J) due to electrons and holes can be expressed as:

\(\displaystyle J = J_n + J_p \)

where (\(\displaystyle J_n = e n \mu_n E \)) and (\(\displaystyle J_p = e p \mu_p E \)), with (E) being the electric field. The electrical conductivity is the current density per unit electric field, so:

\(\displaystyle \sigma = \frac{J}{E} \)

Substituting the expressions for (J_n) and (J_p) into the conductivity equation, we get:

\(\displaystyle \sigma = e (n \mu_n + p \mu_p) \)

Since (n = p = n_i) for intrinsic semiconductors, the expression simplifies to:

\(\displaystyle \sigma = e n_i (\mu_n + \mu_p) \)

This expression tells us that the conductivity of an intrinsic semiconductor depends on the intrinsic carrier concentration and the sum of the mobilities of electrons and holes. It shows that as the number of charge carriers or their mobility increases, the conductivity of the semiconductor also increases.

Extrinsic Semiconductor

An extrinsic semiconductor is a semiconductor material intentionally modified by the introduction of impurities through a process known as doping. Unlike pure intrinsic semiconductors, which exhibit limited electrical conductivity, extrinsic semiconductors are tailored to enhance their electronic properties for specific applications.

Doping introduces controlled amounts of foreign atoms into the semiconductor crystal lattice, altering its electrical behavior by either increasing the concentration of free electrons (N-type doping) or creating additional holes for charge carriers (P-type doping). Understanding the principles of extrinsic semiconductors is essential for advancing semiconductor technology and driving innovation in electronics.

N- Type Semiconductor

N-type semiconductors are materials intentionally doped with impurities that provide excess electrons. The introduction of donor atoms, such as phosphorus, increases the concentration of free electrons in the crystal lattice. These additional electrons become the majority charge carriers, enhancing the material’s electrical conductivity. N-type semiconductors play a crucial role in the construction of electronic devices, contributing to the functionality of transistors and other semiconductor components. The choice of dopant depends on whether you want to create an N-type semiconductor or a P-type semiconductor. Here are some common dopants for both types:

We took antimony (Sb) as a donor impurity in an N-type semiconductor and are discussing its behavior. N-type semiconductors can be created by doping with antimony (Sb) as a donor impurity. Antimony, from Group V of the periodic table, introduces extra electrons into the crystal lattice of the semiconductor material. These additional electrons become the majority charge carriers in the N-type semiconductor, facilitating enhanced electrical conductivity. Antimony-doped N-type semiconductors are commonly used in electronic devices, contributing to their functionality.

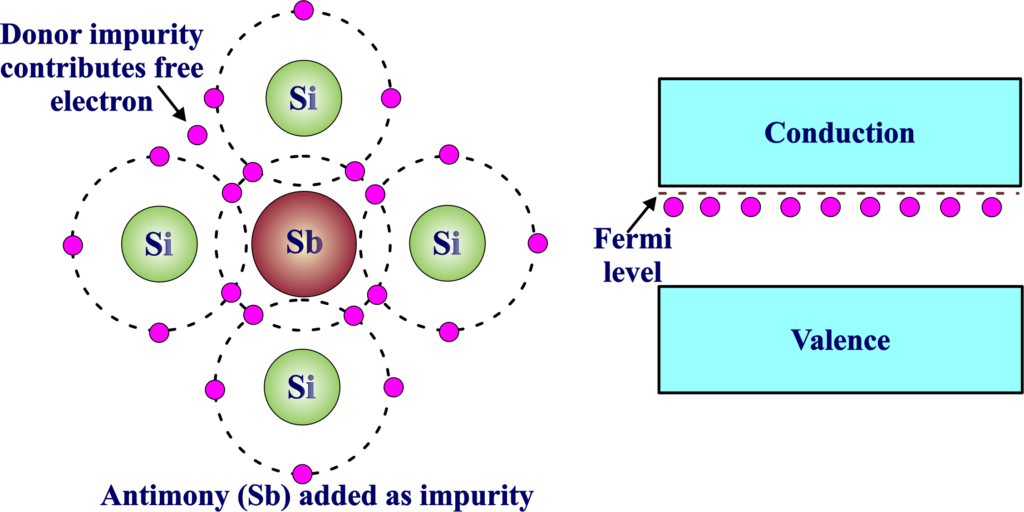
Antimony has five valence electrons (Group V). When antimony is incorporated into the crystal lattice of a semiconductor material like silicon, it replaces a silicon atom and introduces an additional electron. This extra electron becomes a mobile charge carrier.

In an N-type semiconductor doped with antimony, the majority of charge carriers are electrons. These electrons come from the extra electrons introduced by the antimony atoms. The concentration of electrons in the conduction band is higher than the concentration of holes in the valence band.

Fermi Level: The Fermi level is a concept used to describe the energy level at which there is a 50% probability of finding an electron. In an N-type semiconductor, the Fermi level is closer to the conduction band because there are more electrons in the conduction band than in the valence band. The Fermi level plays a crucial role in determining the population of electrons and holes in the material. In equilibrium, the Fermi level remains constant throughout the material, and it helps define the separation between occupied and unoccupied electronic states.

The introduction of antimony as a donor impurity shifts the Fermi level closer to the conduction band, indicating a higher probability of finding electrons at energy levels associated with the conduction band. N-type semiconductors doped with antimony are widely used in electronic devices. These semiconductors are crucial for components like transistors, where efficient electron conduction is essential for amplification and switching functions.

Common dopants for N-type semiconductors introduce extra electrons into the crystal lattice. Examples include:

• Phosphorus (P): Phosphorus is a Group V element and has five valence electrons. When used as a dopant, it introduces an extra electron, creating an N-type semiconductor.
• Arsenic (As): Similar to phosphorus, arsenic is also a Group V element and serves as a dopant to increase electron concentration in the semiconductor.

P- Type Semiconductor

A P-type semiconductor is created by intentionally introducing dopant atoms into a semiconductor material, creating “holes” or vacant electron positions in the crystal lattice. This creates an acceptor level near the valence band, where the gallium atom can accept an electron from a neighboring silicon atom, leaving behind a hole.

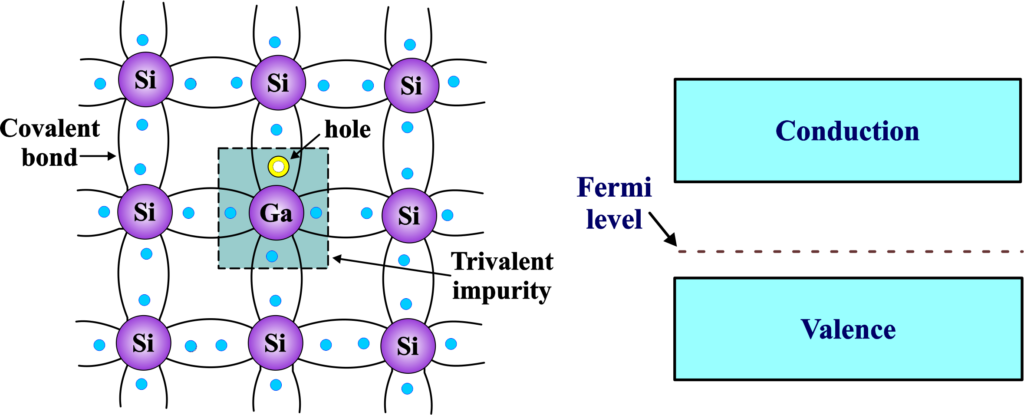
Gallium is a Group III element, meaning it has three valence electrons. When gallium is introduced as a dopant into a semiconductor material, such as silicon, it replaces a silicon atom in the crystal lattice. The incorporation of gallium introduces a deficit of one electron in the crystal lattice because gallium has one less valence electron compared to silicon. This missing electron creates a positively charged vacancy or “hole” in the lattice.

In a P-type semiconductor doped with gallium, the majority of charge carriers are holes. These holes represent positions where electrons are missing, and they act as positive charge carriers when electrons from neighboring atoms move to fill these vacancies. As electrons move to fill the holes created by gallium doping, they leave behind new holes in the lattice. This process creates electron-hole pairs, where holes become the dominant charge carriers.

The fermi level is the energy level where there is a 50% probability of finding an electron at absolute zero temperature. In a p-type semiconductor, the fermi level is closer to the valence band than the conduction band, because there are more holes than electrons. This shift reflects the increased concentration of holes associated with the presence of gallium as a dopant.

P-type semiconductors doped with gallium are essential for the fabrication of various electronic devices, such as PNP transistors and diodes. These devices leverage the flow of positive charge carriers (holes) for their operation.

Common dopants for P-type semiconductors introduce extra “holes” or vacancies into the crystal lattice. Examples include:

• Boron (B):
  • Boron is a Group III element with three valence electrons. When boron is introduced as a dopant in silicon, it creates a “hole” or vacancy in the crystal lattice by accepting an electron from a neighboring silicon atom. This process results in the formation of P-type behavior.
• Aluminum (Al):
  • Aluminum, another Group III element, can be employed as a dopant to achieve P-type behavior. Like boron and gallium, aluminum introduces holes in the crystal lattice.

These dopant elements are from Group III of the periodic table, which means they have fewer valence electrons than the semiconductor host material (like silicon). When they replace silicon atoms in the crystal lattice, they create a deficiency of electrons, leading to P-type conductivity.

Difference Between Intrinsic and Extrinsic Semiconductors

Intrinsic Semiconductors:

• Pure Material: Intrinsic semiconductors are made of a pure semiconductor material without any significant doping.
• Equal Carriers: The number of electrons is equal to the number of holes.
• Temperature Dependent: Their conductivity is highly temperature-dependent because it relies on thermal energy to excite electrons from the valence band to the conduction band.

Extrinsic Semiconductors:

• Doped Material: Extrinsic semiconductors are created by introducing impurities into the intrinsic semiconductor.
• Increased Conductivity: The doping process increases the conductivity significantly.
• Types of Doping:
• N-type: Doping with elements that have more valence electrons than the semiconductor material, adding extra electrons as majority carriers.
• P-type: Doping with elements that have fewer valence electrons, creating holes as majority carriers.

Conceptual Difference:

The primary difference lies in the electrical conductivity and the majority of charge carriers. Intrinsic semiconductors have lower conductivity and equal numbers of electrons and holes. Extrinsic semiconductors have higher conductivity due to the additional charge carriers introduced by doping.

To help students visualize this, you might say that an intrinsic semiconductor is like a classroom where every student (electron) has a seat (hole). When the class is in session (at absolute zero), every seat is taken. As the room warms up (temperature increases), some students stand up (electrons move to the conduction band), leaving empty seats (holes).

In contrast, an extrinsic semiconductor is like a classroom where new students (extra electrons or holes) are brought in. Now, there are either more students than seats (n-type) or more seats than students (p-type), which changes the dynamic of the room (conductivity of the material).

Also Read: Energy Bands In Solids

Examples of Semiconductors

Silicon (Si)

• Most Common: Silicon is the most widely used semiconductor material. It’s abundant, relatively easy to purify, and has properties that make it ideal for a wide range of electronic devices.
• Applications: Used in microchips, transistors, solar cells, and more.

Germanium (Ge)

• Germanium was used in early semiconductor devices before silicon became the preferred material.
• Applications: Still used in some applications like infrared optics and certain transistors.

Gallium Arsenide (GaAs)

• High-Speed Devices: Gallium arsenide is known for its high electron mobility, which makes it suitable for high-speed and high-frequency applications.
• Applications: Used in microwave and millimeter-wave circuits, LEDs, and solar cells.

Indium Phosphide (InP)

• Optoelectronics: Indium phosphide has excellent optoelectronic properties, meaning it can efficiently convert electrical signals into light and vice versa.
• Applications: Used in high-speed and high-frequency electronics, fiber optic communication systems, and photonic devices.

Silicon Carbide (SiC)

• High-Temperature and Power: Silicon carbide can operate at high temperatures and power levels, making it suitable for harsh environments.
• Applications: Used in power electronic devices, such as power converters and high-voltage switches.

Cadmium Selenide (CdSe)

• Quantum Dots: Cadmium selenide is used to make quantum dots, which are tiny semiconductor particles that have unique optical properties due to their size.
• Applications: Used in displays, photodetectors, and solar cells.

These are just a few examples of semiconductors, each with its own set of properties that make it suitable for specific applications.

Solved Examples

Problem 1: Calculate the intrinsic carrier concentration (n_i) in germanium at 300 K. The effective density of states in the conduction band (N_c) is (\(\displaystyle 1.04 \times 10^{19} \text{ cm}^{-3}\)), the effective density of states in the valence band (N_v) is (\(\displaystyle 6.0 \times 10^{18} \text{ cm}^{-3}\)), and the energy gap (E_g) of germanium is 0.66 eV.

Solution: The intrinsic carrier concentration (n_i) is given by:

\(\displaystyle n_i = \sqrt{N_c N_v} e^{-\frac{E_g}{2kT}} \)

Given: E_g = 0.66 eV
\(\displaystyle N_c = 1.04 \times 10^{19} \text{ cm}^{-3}\)
\(\displaystyle N_v = 6.0 \times 10^{18} \text{ cm}^{-3}\)
T = 300 K)
\(\displaystyle k = 8.617 \times 10^{-5} \text{ eV/K}\)

First, calculate the exponential term:

\(\displaystyle \frac{E_g}{2kT} = \frac{0.66}{2 \times 8.617 \times 10^{-5} \times 300} = \frac{0.66}{0.051702} \approx 12.76 \)

Now, calculate the intrinsic carrier concentration:

\(\displaystyle n_i = \sqrt{1.04 \times 10^{19} \times 6.0 \times 10^{18}} e^{-12.76}\)
\(\displaystyle n_i = \sqrt{6.24 \times 10^{37}} e^{-12.76} \)
\(\displaystyle n_i = 2.5 \times 10^{18} e^{-12.76} \)

\(\displaystyle e^{-12.76} \approx 2.85 \times 10^{-6} \)

So,

\(\displaystyle n_i \approx 2.5 \times 10^{18} \times 2.85 \times 10^{-6} \)
\(\displaystyle n_i \approx 7.12 \times 10^{12} \text{ cm}^{-3} \)

Therefore, the intrinsic carrier concentration in germanium at 300 K is approximately (\(\displaystyle 7.12 \times 10^{12} \text{ cm}^{-3}\).

Problem 2: Given the electron mobility (µ_n) in silicon is (\(\displaystyle 1350 \text{ cm}^2/\text{V·s}\)) and the hole mobility (µ_p) is (\(\displaystyle 480 \text{ cm}^2/\text{V·s}\)), calculate the total conductivity of intrinsic silicon at 300 K. The intrinsic carrier concentration (n_i) is (\(\displaystyle 1.5 \times 10^{10} \text{ cm}^{-3}\).

Solution: The conductivity (\sigma) of an intrinsic semiconductor is given by:

\(\displaystyle \sigma = q n_i (\mu_n + \mu_p) \)

where (q) is the charge of an electron (\(\displaystyle 1.6 \times 10^{-19} \text{ C}\).

Given:
\(\displaystyle \mu_n = 1350 \text{ cm}^2/\text{V·s}\)
\(\displaystyle\mu_p = 480 \text{ cm}^2/\text{V·s}\)
\(\displaystyle n_i = 1.5 \times 10^{10} \text{ cm}^{-3}\)

Calculate the conductivity:

\(\displaystyle\sigma = 1.6 \times 10^{-19} \times 1.5 \times 10^{10} \times (1350 + 480) \)
\(\displaystyle\sigma = 1.6 \times 1.5 \times 1830 \times 10^{-9} \text{ S/cm} \)
\(\displaystyle\sigma = 2.4 \times 1830 \times 10^{-9} \text{ S/cm} \)
\(\displaystyle\sigma = 4392 \times 10^{-9} \text{ S/cm} \)
\(\displaystyle\sigma = 4.392 \times 10^{-6} \text{ S/cm} \)

Therefore, the conductivity of intrinsic silicon at 300 K is approximately (\(\displaystyle 4.392 \times 10^{-6} \text{ S/cm}\).

Problem 3: Calculate the Fermi level position (E_F) in intrinsic silicon at 300 K. The bandgap (E_g) is 1.12 eV, and the effective density of states in the conduction band (N_c) and valence band (N_v) are (\(\displaystyle 2.8 \times 10^{19} \text{ cm}^{-3}\)) and (\(\displaystyle 1.04 \times 10^{19} \text{ cm}^{-3}\)) respectively.

Solution: In an intrinsic semiconductor, the Fermi level (E_F) is given by:

\(\displaystyle E_F = \frac{E_c + E_v}{2} + \frac{3}{4} kT \ln \left( \frac{N_v}{N_c} \right) \)

Given:
E_g = 1.12 eV
\(\displaystyle E_c = E_v + E_g\)
\(\displaystyle N_c = 2.8 \times 10^{19} \text{ cm}^{-3}\)
\(\displaystyle N_v = 1.04 \times 10^{19} \text{ cm}^{-3}\)
T = 300 K
\(\displaystyle k = 8.617 \times 10^{-5} \text{ eV/K}\)

Calculate the logarithmic term:

\(\displaystyle \ln \left( \frac{N_v}{N_c} \right) = \ln \left( \frac{1.04 \times 10^{19}}{2.8 \times 10^{19}} \right) = \ln (0.3714) \approx -0.991 \)

Now, calculate the Fermi level position:

\(\displaystyle E_F = \frac{E_v + (E_v + E_g)}{2} + \frac{3}{4} kT \ln \left( \frac{N_v}{N_c} \right) \)
\(\displaystyle E_F = \frac{2E_v + 1.12}{2} + \frac{3}{4} \times 8.617 \times 10^{-5} \times 300 \times (-0.991) \)
\(\displaystyle E_F = E_v + 0.56 – 0.191 \)
\(\displaystyle E_F = E_v + 0.369 \text{ eV} \)

Therefore, the Fermi level in intrinsic silicon at 300 K is approximately (\(\displaystyle 0.369 \text{ eV}\)) above the valence band edge.

Problem 4: A silicon sample is doped with (\(\displaystyle 5 \times 10^{15}\)) phosphorus atoms per cm³. Calculate the conductivity of the n-type silicon at 300 K. Assume the electron mobility (µ_n) is (\(\displaystyle 1350 \text{ cm}^2/\text{V·s}\)).

Solution: In n-type silicon, the majority of carriers are electrons, and the carrier concentration (n) is approximately equal to the doping concentration (N_D).

Given:
\(\displaystyle N_D = 5 \times 10^{15} \text{ cm}^{-3}\)
\(\displaystyle\mu_n = 1350 \text{ cm}^2/\text{V·s}\)
\(\displaystyle q = 1.6 \times 10^{-19} \text{ C}\)

The conductivity (σ) is given by:

\(\displaystyle\sigma = q n \mu_n \)

Since (\(\displaystyle n \approx N_D\)):

\(\displaystyle\sigma = 1.6 \times 10^{-19} \times 5 \times 10^{15} \times 1350 \)
\(\displaystyle\sigma = 1.6 \times 5 \times 1350 \times 10^{-4} \text{ S/cm}\)
\(\displaystyle\sigma = 10800 \times 10^{-4} \text{ S/cm} \)
\(\displaystyle\sigma = 1.08 \text{ S/cm} \)

Therefore, the conductivity of the n-type silicon at 300 K is approximately (\(\displaystyle 1.08 \text{ S/cm}\)).

FAQs