The story of uniform circular motion begins with the ancient Greeks. Aristotle was one of the first to observe that celestial bodies like the stars and planets moved in what seemed to be perfect circles in the sky. He believed that the heavens were perfect and unchanging, and thus the circular motion was the most fitting.
Fast forward to the Renaissance, and the narrative takes a significant turn with Nicolaus Copernicus. He proposed the revolutionary idea that the Earth and other planets revolved around the Sun in circular orbits. This heliocentric model was a stark departure from the Earth-centered model of the universe that had been widely accepted for centuries.
Tycho Brahe, an astronomer known for his incredibly precise observations of the stars and planets, provided the data that would later be crucial in understanding uniform circular motion. Although he didn’t believe in Copernicus’s heliocentric model, his detailed records were invaluable.
Using Brahe’s data, Johannes Kepler discovered that the planets’ orbits were not perfect circles but ellipses, with the Sun at one focus. However, his work on orbital motion laid the groundwork for understanding motion in a central force field, which is key to understanding uniform circular motion.
Finally, Sir Isaac Newton formulated his laws of motion and universal gravitation, which explained why planets and other objects followed elliptical paths and how they could move in uniform circular motion under certain conditions. Newton’s laws provided the mathematical framework to describe uniform circular motion fully.
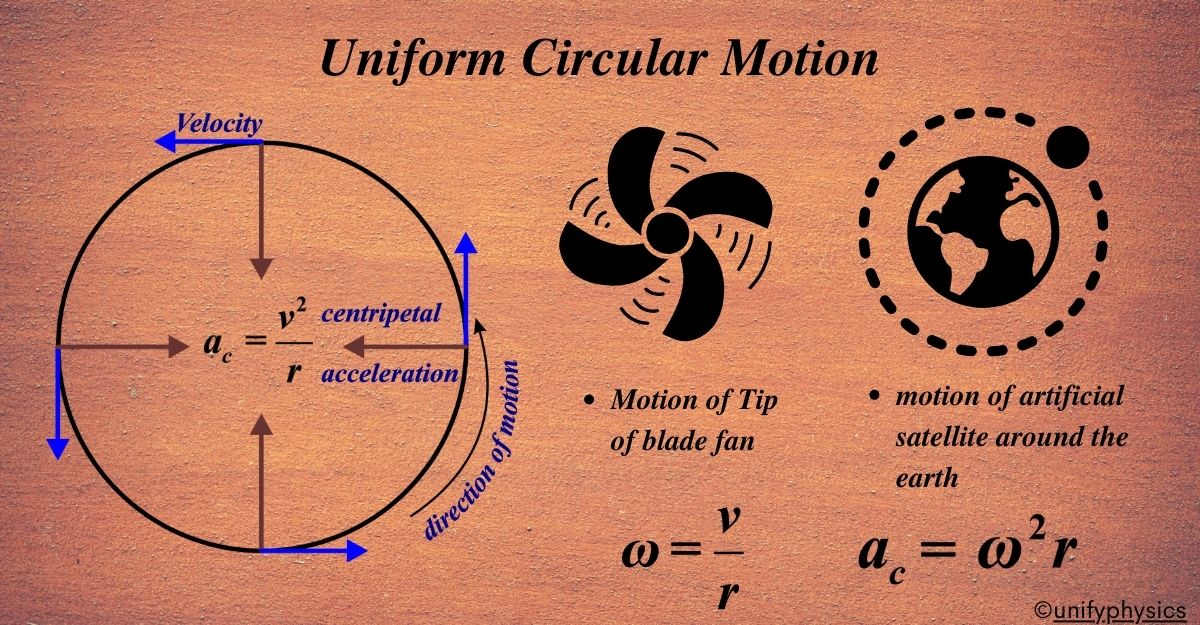
Today, we understand uniform circular motion as the motion of an object traveling in a circular path at a constant speed. The direction of the object’s velocity changes continuously, making it an accelerated motion, even though the speed is constant. This concept is fundamental in physics and is applied in everything from designing roller coasters to understanding the orbits of satellites.
Uniform circular motion is a tale of observation, revolution, and mathematical genius. It’s a journey from the ancient Greeks’ star-gazing to the precise calculations that allow us to send satellites into space and explore the universe beyond our planet.
What Is Uniform Circular Motion?
Uniform Circular Motion (UCM) occurs when an object moves along a circular path at a constant speed. While the speed remains unchanged, the direction of velocity is continuously changing, making UCM an accelerated motion due to the constant change in direction.
Imagine you’re on a merry-go-round. You’re moving in a circle, and if the merry-go-round is spinning at a steady rate, you’re experiencing uniform circular motion. In UCM, an object moves along a circular path with a constant speed—not velocity, but speed. That’s an important distinction because even though the speed doesn’t change, the direction of the object’s velocity is always changing as it moves around the circle.
Constant Speed, Changing Direction: The key to UCM is that the object keeps the same speed around the circle. But since it’s constantly changing direction, it’s accelerating. This might seem strange because we usually think of acceleration as speeding up or slowing down. In UCM, the acceleration comes from the change in direction, not speed.
What keeps an object moving in a circle? It’s a force called centripetal force. This force is always directed towards the center of the circle and is what causes the object to follow a curved path. Without this force, the object would fly off in a straight line.
In UCM, while the speed is constant, the velocity is not. Velocity is speed with direction. Since the direction is always changing as the object moves around the circle, the velocity is constantly changing too—even though the speed is steady.
The Role of Acceleration: Because the direction of velocity changes, there’s always an acceleration towards the center of the circle, known as centripetal acceleration. This acceleration is perpendicular to the velocity of the object at every instant, which means it only changes the direction of the velocity, not its magnitude.
In true UCM, there’s no acceleration along the tangent to the circle—that’s why the speed is constant. If there were tangential acceleration, the speed would change, and the motion would no longer be uniform⁴.
The mathematics of UCM involves the relationship between the speed of the object, the radius of the circle, and the centripetal acceleration. The formula is
\(\displaystyle\begin{equation}\label{eqn:1}\boxed{\boldsymbol{a_{c} = \frac{v^2}{r} }} \end{equation}\)
where (ac) is the centripetal acceleration, (v) is the speed, and (r) is the radius of the circle.
Understanding UCM is crucial for many real-world applications, from designing car tires that can grip the road during turns to calculating the orbits of satellites. It’s a fundamental concept that shows how even a constant speed can lead to acceleration due to a change in direction.
Centripetal Acceleration
In UCM, the centripetal acceleration is the acceleration directed towards the center of the circle. It’s responsible for changing the direction of velocity, and keeping the object in circular motion.
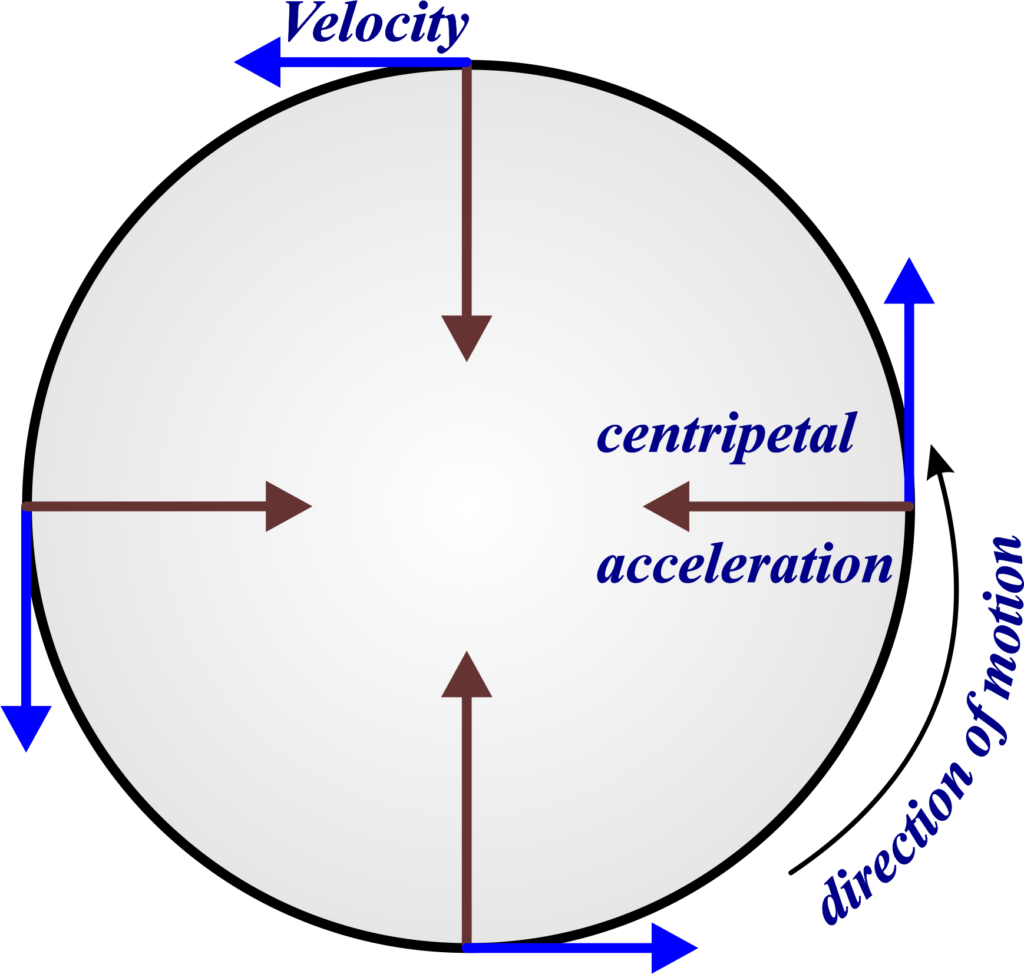
Think of centripetal acceleration as the unseen force that keeps a car turning on a curved track instead of shooting straight off the road. It’s the same thing that keeps you pressed against the wall in a spinning carnival ride.
Centripetal acceleration is the acceleration that occurs when an object moves in a circular path.
It always points towards the center of the circle and is responsible for changing the direction of the object’s velocity.
- Direction Matters: Even if an object is moving at a constant speed in a circle, its velocity is changing because velocity includes direction. Since the direction is always changing in a circle, the velocity is too.
- Towards the Center: The acceleration is directed radially inward, towards the center of the circle. This inward pull is what keeps the object moving in a circle.
- The Formula: The magnitude of centripetal acceleration (ac) is calculated by the formula \(\displaystyle (a_c = \frac{v^2}{r})\), where (v) is the speed of the object, and (r) is the radius of the circular path.
- Units: Just like any acceleration, centripetal acceleration is measured in meters per second squared (m/s2).
Examples: When you take a sharp turn in a car, you’re experiencing centripetal acceleration pulling you into the curve.
- Planets: Earth’s orbit around the Sun involves centripetal acceleration keeping it in a nearly circular path.
- Sports: A figure skater pulling in their arms to spin faster is creating a greater centripetal acceleration by reducing the radius of their spin.
Experiment: A simple experiment to understand this concept is to tie a ball to a string and spin it in a circle. The string is pulling the ball towards the center, providing the centripetal force, and the ball’s change in direction is a result of the centripetal acceleration.
Centripetal acceleration is essential for anything that moves in a circle. Without it, objects would move in straight lines, and circular motion as we know it wouldn’t exist.
Also Read: Acceleration
Equations of Motion for Uniform Circular Motion
The equations of motion for UCM relate the centripetal acceleration to the tangential velocity (v) and the radius (r) of the circular path.
At the heart of UCM is a simple yet powerful equation that relates the speed of an object moving in a circle to the radius of that circle and the centripetal acceleration it experiences:
\(\displaystyle a_{c} = \frac{v^2}{r} \)
- (ac) is the centripetal acceleration, directed towards the center of the circle.
- (v) is the constant speed of the object in the circular path.
- (r) is the radius of the circular path.
Centripetal Acceleration tells us how much the object is accelerating toward the center of the circle. Even though the object’s speed is constant, this acceleration is what keeps changing its direction. The constant speed in UCM is the rate at which the object moves along the circumference of the circle. The distance from the center of the circle to the object. A larger radius means a larger circle for the object to move around.
Angular Relationships: In UCM, we often talk about angular speed (ω), which is the rate at which the object rotates around the circle:
\(\displaystyle\begin{equation}\label{eqn:2}\boxed{\boldsymbol{\omega = \frac{v}{r} }} \end{equation}\)
The centripetal acceleration can also be expressed in terms of angular speed:
\(\displaystyle\begin{equation}\label{eqn:3}\boxed{\boldsymbol{a_{c} = \omega^2 r }} \end{equation}\)
This shows that the centripetal acceleration is proportional to the square of the angular speed and the radius of the circle.
Mass: When we introduce mass (m) into the equation, we get the centripetal force (Fc) required to keep the object in circular motion:
\(\displaystyle F_{c} = m \cdot a_c \)
Time Period and Frequency: Two other important concepts in UCM are the time period (( T )) and frequency (( f )):
- Time Period (T): The time it takes for one complete revolution around the circle.
- Frequency (f): The number of complete revolutions per second, which is the inverse of the time period (\(\displaystyle f = \frac{1}{T} \)).
These equations of motion for UCM allow us to predict and understand the behavior of objects in circular paths. So, when you’re spinning a ball on a string or watching the planets move in the night sky.
Nonuniform Circular Motion
Nonuniform Circular Motion differs from UCM in that the speed of the object is not constant. It involves both radial (centripetal) acceleration and tangential acceleration, which changes the magnitude of velocity. This type of motion is more complex and requires additional forces to maintain the circular path.
Imagine you’re on a merry-go-round that’s starting to speed up or slow down while you’re going around in a circle. This is different from uniform circular motion, where the speed is constant. In nonuniform circular motion, the speed of the object changes as it moves along the circular path.
Characteristics
- Changing Speed: Unlike uniform circular motion, the object’s speed in nonuniform circular motion is not constant. It can speed up or slow down.
- Velocity Vector: The velocity vector is always tangent to the circle, meaning it points along the path the object is moving at any instant.
- Angular Speed: The angular speed (how fast the object is rotating around the circle) is not constant, which means the object can rotate faster or slower at different times.
- Angular Acceleration: There’s an angular acceleration present, which means the rate at which the object is rotating around the circle is changing.
Components of Acceleration: In nonuniform circular motion, the acceleration vector doesn’t just point toward the center of the circle. It has two components:
- Radial Acceleration (aR): Directed towards the center of the circle, responsible for changing the direction of the velocity.
- Tangential Acceleration (aT): Tangent to the circle, responsible for changing the speed of the object.
The radial component of acceleration is given by the same formula as in uniform circular motion:
\(\displaystyle a_{R} = \frac{v^2}{r} \)
However, the speed (v) is no longer constant over time. The tangential acceleration, which changes the speed, is given by:
\(\displaystyle a_{T} = \frac{dv}{dt} \)
where (dv/dt) is the rate of change of speed with respect to time.
Examples:
- Cars on a Curvy Road: When a car speeds up or brakes while turning, it’s undergoing nonuniform circular motion.
- Roller Coasters: As a roller coaster car goes through loops, it often speeds up and slows down, which is a perfect example of nonuniform circular motion.
Nonuniform circular motion is important for designing safe amusement park rides, understanding the orbits of comets (which can speed up and slow down), and many other practical applications.
Solved Examples
Problem 1: A particle moves in a circular path of radius (2 m) with a constant speed of (3 m/s). Calculate the centripetal acceleration.
Solution: Centripetal acceleration (ac) is given by:
\(\displaystyle a_c = \frac{v^2}{r} \)
Where: v = 3 m/s; r = 2 m
\(\displaystyle a_c = \frac{3^2}{2} = \frac{9}{2} = 4.5 \, \text{m/s}^2 \)
Thus, the centripetal acceleration is (4.5 m/s2 ).
Problem 2: A ball of mass (0.5 kg) is attached to a string and swung in a horizontal circle of radius (1 m) with a speed of (4 m/s). Calculate the tension in the string.
Solution: The tension in the string provides the centripetal force:
\(\displaystyle T = F_c = \frac{mv^2}{r} \)
Where: m = 0.5 kg; v = 4 m/s; r = 1 m.
\(\displaystyle T = \frac{0.5 \times 4^2}{1} = \frac{0.5 \times 16}{1} = 8 \, \text{N} \)
Thus, the tension in the string is (8 N).
Problem 3: A toy car moves in a circular track of radius (10 m) with a speed of (5 m/s). Calculate the period of rotation.
Solution: The period (T) is given by:
\(\displaystyle T = \frac{2\pi r}{v} \)
Where: r = 10 m; v = 5 m/s.
\(\displaystyle T = \frac{2\pi \times 10}{5} = \frac{20\pi}{5} = 4\pi \, \text{s} \approx 12.57 \, \text{s} \)
Thus, the period of rotation is approximately (12.57 s).
Problem 4: A particle moves in a circular path of radius (4 m) with an angular acceleration of (2 rad/s2) and an initial angular velocity of (3 rad/s). Calculate the tangential and radial accelerations after (5 s).
Solution: The tangential acceleration (at) is given by:
\(\displaystyle a_t = r \alpha \)
Where: r = 4 m; \(\displaystyle\alpha = 2 \, \text{rad/s}^2 \)
\(\displaystyle a_t = 4 \times 2 = 8 \, \text{m/s}^2 \)
The angular velocity (ω) after (5 s) is given by:
\(\displaystyle \omega = \omega_0 + \alpha t \)
Where: \(\displaystyle\omega_0 = 3 \, \text{rad/s}\); t = 5 s.
\(\displaystyle \omega = 3 + 2 \times 5 = 3 + 10 = 13 \, \text{rad/s} \)
The radial acceleration (ar) is given by:
\(\displaystyle a_r = r \omega^2 \)
\(\displaystyle a_r = 4 \times 13^2 = 4 \times 169 = 676 \, \text{m/s}^2\)
Thus, the tangential acceleration is (8 m/s2) and the radial acceleration is (676 m/s2).
Problem 5: A car of mass (1200 kg) is taking a turn on a flat road with a radius of (100 m). If the coefficient of friction between the tires and the road is (0.4), calculate the maximum speed the car can achieve without skidding.
Solution: The maximum centripetal force is provided by friction:
\(\displaystyle F_c = \mu mg \)
This force also equals the centripetal force required:
\(\displaystyle F_c = \frac{mv^2}{r} \)
Equating the two:
\(\displaystyle \mu mg = \frac{mv^2}{r} \)
\(\displaystyle v^2 = \mu gr \)
Where: µ = 0.4; g = 9.8 m/s2 ; r = 100 m.
\(\displaystyle v^2 = 0.4 \times 9.8 \times 100 \)
\(\displaystyle v^2 = 392 \)
\(\displaystyle v = \sqrt{392} \approx 19.8 \, \text{m/s} \)
Thus, the maximum speed without skidding is (19.8 m/s).
Problem 6: A wheel starts from rest and has an angular acceleration of (3 rad/s2). Calculate the angular displacement after (4 s).
Solution: The angular displacement (θ) is given by:
\(\displaystyle \theta = \omega_0 t + \frac{1}{2} \alpha t^2 \)
Where: \(\displaystyle\omega_0 = 0 \, \text{rad/s} \)) (starts from rest); \(\displaystyle\alpha = 3 \, \text{rad/s}^2 \); t = 4 s.
\(\displaystyle \theta = 0 \times 4 + \frac{1}{2} \times 3 \times 4^2\)
\(\displaystyle \theta = \frac{1}{2} \times 3 \times 16 \)
\(\displaystyle \theta = 24 \, \text{rad} \)
Thus, the angular displacement after (4 s) is (24 rad).
FAQs
What is uniform circular motion, and how does it differ from other types of motion?
Uniform circular motion is the motion of an object traveling in a circular path at a constant speed. Unlike linear motion, where the direction of motion is straight, uniform circular motion involves a continuous change in direction while maintaining a constant speed.
What are the key characteristics of objects undergoing uniform circular motion?
In a uniform circular motion, the speed of the object remains constant, but its direction continuously changes as it moves around the circular path. Additionally, the object experiences centripetal acceleration directed towards the center of the circle.
How do we calculate the centripetal acceleration of an object in uniform circular motion?
Centripetal acceleration, denoted by (ac), is calculated using the formula:
\(\displaystyle a_{c} = \frac{v^2}{r}\)
where (v) is the speed of the object and (r) is the radius of the circular path.
Can you explain the difference between centripetal acceleration and tangential acceleration in uniform circular motion?
Centripetal acceleration is the acceleration directed towards the center of the circular path, required to keep an object moving in a circular motion. Tangential acceleration, on the other hand, is the acceleration along the tangent to the circle at any given point, representing changes in the speed of the object.
What role does centripetal force play in uniform circular motion?
Centripetal force is the force directed toward the center of the circular path that is required to maintain an object’s uniform circular motion. It is provided by various forces, such as tension in a string, gravitational force, or friction, depending on the specific situation.
How does the radius of the circular path affect the speed and centripetal acceleration of an object in uniform circular motion?
As the radius of the circular path increases, the speed of the object can remain constant, but the centripetal acceleration decreases. Conversely, if the radius decreases, the centripetal acceleration increases for the same speed.
Can you provide an example of uniform circular motion from everyday life?
A common example of uniform circular motion is a car traveling around a roundabout at a constant speed. As the car moves around the circular path, its speed remains constant, but it continuously changes direction, experiencing uniform circular motion.