The Van de Graaff Generator, a remarkable invention in the field of electrostatics, was the brainchild of Robert J. Van de Graaff, an American physicist. He conceptualized and built the first model in 1929. The generator was not just a product of sudden inspiration; it was an evolution of ideas that began with the Kelvin water dropper invented by William Thomson (Lord Kelvin) in 1867.
The Kelvin water dropper was an early electrostatic generator that used falling water drops to accumulate electric charge. Lord Kelvin suggested that a belt could be used instead of water to transport charge, which led to the first belt-driven electrostatic machine by Augusto Righi in 1872.
Van de Graaff’s generator was initially developed to serve as a particle accelerator for physics research. It was capable of generating high voltages that could accelerate subatomic particles to great speeds, making it the most powerful type of accelerator before the cyclotron came into play in the early 1930s.
The first Van de Graaff generator was a modest device, but it laid the foundation for larger and more powerful generators. For instance, the Westinghouse Atom Smasher, built in 1937, was a 5 MeV Van de Graaff generator. Over time, improvements were made, and by 1952, a Van de Graaff generator in Hungary achieved 1000 kV.
The Van de Graaff generator’s design was inspired by an earlier electrostatic generator called the Pelletron, invented by physicist John D. Cockcroft in 1932. Van de Graaff’s version aimed to produce much higher voltages than previous generators, which were limited by the size of the plates used for charge accumulation.
Today, while Van de Graaff generators are largely used for educational purposes, they continue to be a testament to the ingenuity of scientists who harnessed the power of electrostatics to advance research in nuclear physics and medicine. They remind us that great scientific achievements often stand on the shoulders of the ideas and inventions that came before them.
What is Van de Graaff Generator?
It’s a device that generates static electricity and accumulates it on a large metal sphere, creating high electric potentials. Imagine you’re at a science museum, and you see a large metal ball mounted on a pedestal. You’re told it’s a Van de Graaff Generator, and when it’s turned on, someone’s hair stands on end! This is not just a fun exhibit; it’s a sophisticated scientific device.
A Van de Graaff Generator is like a big balloon that can hold a lot of static electricity, similar to the static charge you get when you rub a balloon on your hair. But instead of a balloon, it uses a large metal sphere and can generate much more static electricity—enough to make your hair stand up without even touching it!
It has a motor that moves a rubber belt inside the column. As the belt moves, it rubs against rollers, which builds up static electricity through a process called the triboelectric effect. This is the same effect that happens when you shuffle your feet on a carpet and then touch a doorknob, resulting in a small shock.
The static charge is carried up by the belt to the metal sphere at the top. There, a brush made of metal wires ‘paints’ the charge onto the sphere. Because the sphere is so smooth and round, the charge spreads out evenly all over its surface.
The sphere is made of metal, which is a conductor, so it’s good at holding onto the charge. The belt is made of rubber, which is an insulator, so it doesn’t hold onto the charge as well.
The sphere can accumulate a huge amount of charge, much more than the balloon in our earlier example. This charge creates a strong electric field around the sphere, which can cause the air around it to ionize, leading to a spark or a corona discharge.
In simple terms, a Van de Graaff Generator is a machine that creates a big static charge and stores it on a metal ball. It’s like a super-powered version of rubbing a balloon on your hair, and it’s used in science to study electricity and to do cool experiments.
Principle of Van de Graaff Generator
The Van de Graaff Generator operates on a very simple yet fascinating principle of electrostatics, which is the study of stationary or slow-moving electric charges, where a moving belt creates static electricity through friction and transfers it to the sphere.
Imagine you have a wool sweater and a plastic rod. When you rub them together, they get charged due to the triboelectric effect. This is because some materials tend to give up electrons (the sweater), while others tend to grab them (the plastic rod). Now, if you could collect these charges and move them to a metal ball, you’d have a basic Van de Graaff Generator!
A motor moves a rubber belt inside a column. The belt passes over rollers made of different materials, which causes it to pick up a charge—just like the sweater and the rod. This charge is then transferred to a large metal sphere at the top of the generator. Because the sphere is a conductor, it allows the charges to spread out evenly over its surface. The larger the sphere, the more charge it can hold without discharging.
The key idea here is that charges repel each other. So, as more and more charge is added to the sphere, the charges push away from each other, trying to get as far apart as possible. This creates a very high voltage on the surface of the sphere—high enough to make the air around it start to break down and conduct electricity, which can lead to sparks or a corona discharge.
The Van de Graaff Generator, a fascinating device used in physics demonstrations and experiments, operates on the principle of charge separation, accumulation, electric field generation, and charge transfer.
Charge Separation
The journey begins with the separation of charges. The generator uses a rubber belt moving between two rollers to create friction, similar to rubbing a balloon on your hair. This friction causes electrons to be scraped off one material and transferred to another, creating an imbalance of charges.
The belt, now carrying extra electrons, moves upwards towards the dome at the top of the generator. These electrons are negative charges that have been separated from their neutral atoms. At the top, a metal brush or comb takes these extra electrons and transfers them to the metal dome.
The dome, being conductive, allows these charges to spread out over its surface. As more and more electrons accumulate on the dome, they repel each other because like charges repel. They want to get as far away from each other as possible, but they’re trapped on the dome. This repulsion between the electrons creates a high electric potential (voltage).
Charge Accumulation
The Van de Graaff Generator can be likened to a giant piggy bank, but instead of storing coins, it stores electric charges. Just like saving money starts with a single coin, charge accumulation starts with a single charge.
The generator uses a rubber belt to pick up extra electrons (which are negative charges) from a lower roller. The belt then carries these electrons up to the top of the generator, just like an elevator going up to the top floor of a building. At the top, there’s a metal brush that acts like a teller at a bank. It takes the electrons from the belt and deposits them onto the metal sphere (the dome).
The metal sphere is a good conductor, so the electrons spread out evenly across its surface. They want to get as far away from each other as possible because like charges repel. As more and more electrons are added, the sphere’s electric potential (voltage) gets higher and higher. It’s like the piggy bank getting fuller and fuller.
Electric Field Generation
The Van de Graaff Generator is not just a device for creating sparks; it’s also a brilliant example of electric field generation. An electric field is created around any charged object. In the case of the Van de Graaff Generator, as the dome gets more and more charged, the electric field around it gets stronger and stronger.
This field is a vector field, which means it has both magnitude and direction. The direction of the electric field is always away from the dome because the dome is negatively charged. The strength of the electric field (E) is directly related to the amount of charge (Q) on the dome and inversely related to the square of the distance (r) from the dome. It’s given by the formula:
\(\displaystyle E = \frac{k \cdot Q}{r^2} \)
where (k) is Coulomb’s constant. This electric field can exert forces on other charges nearby. If a positive charge is brought close to the dome, it will be attracted toward the dome, and if a negative charge is brought close, it will be repelled.
Charge Transfer
The Van de Graaff Generator is like a big, static electricity pump. It moves electric charges from one place to another. At the bottom of the generator, there’s a metal brush or comb connected to a high-voltage power supply. This brush deposits a positive charge onto the belt.
The belt, which is made of an insulating material, carries this positive charge up to the top of the generator. It’s like an escalator for electric charges, moving them from the ground floor to the top floor. Inside the large metal sphere at the top, another metal brush waits for the belt. This brush does the opposite of the first one: it removes the charge from the belt and deposits it onto the sphere’s inner surface.
Once the charge is on the sphere, it doesn’t just sit in one spot. Because like charges repel each other, the positive charges push away from each other until they’re spread out all over the sphere’s surface.
As more and more charge is transferred to the sphere, the electric potential (voltage) of the sphere increases. This is because the charges are trying to get as far away from each other as possible, but they’re confined to the surface of the sphere.
The Van de Graaff Generator is a clever use of basic physics principles to create a machine that can generate and store a large amount of static electricity. It’s a perfect example of how understanding the behavior of charges can lead to the development of fascinating devices!
In conclusion, the Van de Graaff Generator is a remarkable device that demonstrates the principles of static electricity on a grand scale. It separates, accumulates, and transfers charges, creating a high voltage that can be used for various experiments or just for making your hair stand on end for fun!
Construction of Van de Graaff Generator
It consists of a large hollow metal sphere on top of an insulating column, with a motor-driven belt that transports charge to the sphere.
Dome: The dome of a Van de Graaff Generator is typically a large, hollow, and smooth metal sphere. It’s designed to minimize sharp edges or points where electrical discharge could occur. The dome collects and stores the static electric charge generated by the machine.
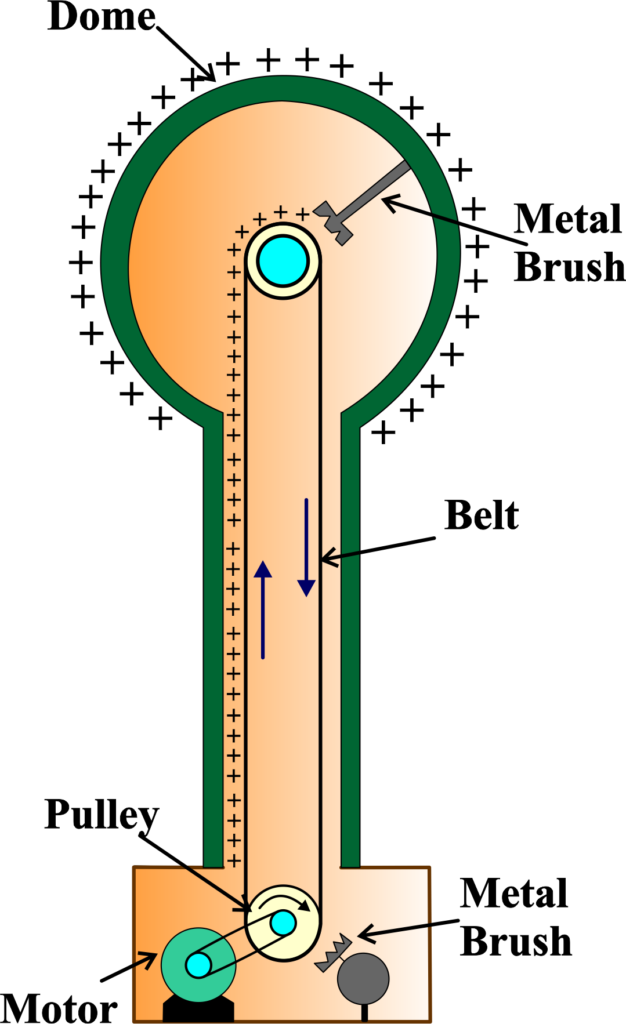
Belt: The belt is a key component made of an insulating material, such as rubber. It runs continuously over two pulleys and acts like a conveyor belt for electric charge. As it moves, it picks up electric charge from the bottom and carries it to the top of the generator.
Pulleys: There are two pulleys in the Van de Graaff Generator. One is located at the base, connected to the motor, and the other is inside the dome at the top. The belt runs over these pulleys, and their rotation enables the transfer of charge.
Metal Sphere: This is the dome we mentioned earlier. It’s where the charge transferred by the belt accumulates. The sphere’s large size allows it to store a significant amount of charge, leading to high potential differences.
Metal Sphere: This is the dome we mentioned earlier. It’s where the charge transferred by the belt accumulates. The sphere’s large size allows it to store a significant amount of charge, leading to high potential differences.
Metal Brush (Collector): At the top of the column, near the dome, there’s a metal brush or a set of sharp points. This brush collects the charge from the belt and transfers it to the dome. The brush is made of conductive material and is designed to efficiently transfer charge without sparking.
Motor: The motor is the driving force of the generator. It turns the bottom pulley, which in turn moves the belt. The motor needs to be powerful enough to keep the belt moving smoothly, even as it carries a high electric charge.
The Van de Graaff Generator is constructed with these components working together to create and store static electricity. The belt system transports charge to the dome, where it accumulates and can be used for various experiments and demonstrations. It’s a brilliant example of how simple mechanical parts can be used to achieve impressive electrical phenomena!
Working of Van de Graaff Generator
The Van de Graaff Generator is like a big pump for electric charges, but instead of pumping water, it pumps static electricity. Here’s how it works step by step:
- Starting the Engine: The generator has a motor that starts the whole process. When the motor runs, it moves a rubber belt inside the column of the generator.
- Rubbing for Charge: As the belt moves, it passes through rollers that rub against it. This rubbing action is similar to when you rub a balloon on your hair and it sticks. This process is known as the triboelectric effect, and it causes the belt to pick up negative charges (electrons).
- Climbing Up: The charged belt then moves upwards towards the top of the generator, carrying the electrons with it.
- Transfer of Charge: At the top, there’s a metal brush or comb that ‘brushes’ against the belt. This brush is connected to the inside of the metal dome. When the charged belt touches the brush, the electrons jump from the belt to the dome.
- Spreading Out: The metal dome collects these electrons. Since like charges repel each other, the electrons try to get as far away from each other as possible, spreading out over the surface of the dome.
- High Voltage: As more and more electrons accumulate on the dome, the electric potential (voltage) of the dome increases. This can create a potential difference of several million volts!
- Discharge: If the voltage gets high enough, the air around the dome can’t hold the electrons anymore, and they jump off, creating sparks or a purple glow called a corona discharge.
In simple terms, the Van de Graaff Generator works by using a moving belt to transfer static charge to a metal dome, where the charge builds up to create high voltages. It’s a brilliant demonstration of the basic principles of electricity and electrostatics in action!
Potential Difference in a Van de Graaff Generator
The potential difference in a Van de Graaff Generator is the high voltage created between the charged sphere and the ground. This voltage can be quite significant, with modern Van de Graaff generators capable of achieving as much as 5 megavolts. A tabletop version can produce around 100 kV and can store enough energy to produce visible electric sparks.
The potential difference is created by the movement of a belt within the generator, which transports charge to the metal sphere at the top. As more charge is added to the sphere, the electric potential increases because the sphere wants to repel the additional like charges. This buildup of charge creates a strong electric field around the sphere. If the sphere’s potential becomes high enough compared to its surroundings, the electric field can cause the air around the sphere to ionize, leading to a spark or corona discharge.
This potential difference is essential for the generator’s use as a particle accelerator, where it can accelerate charged particles to high speeds for scientific research. It’s also what allows for the dramatic demonstrations often associated with Van de Graaff generators, such as making hair stand on end or creating sparks that jump to nearby conductors.
The potential difference in a Van de Graaff Generator, which is the voltage across the sphere, can be calculated using the formula for the electric potential (V) of a point charge. Since the sphere behaves like a point charge at its center, the formula is:
\(\displaystyle V = \frac{k \cdot Q}{R} \)
- (V) is the electric potential or potential difference (in Volts),
- (k) is Coulomb’s constant (\(\displaystyle8.9875 \times 10^9 ) N·m²/C²\)),
- (Q) is the charge on the sphere (in Coulombs),
- (R) is the radius of the sphere (in meters).
This formula assumes that the potential at infinity is zero and that the charge is uniformly distributed over the sphere’s surface. The potential difference calculated is the voltage of the sphere relative to the ground or another reference point at a much larger radius where the potential is considered zero.
Potential developed on the surface of the larger sphere:
The Van de Graaff Generator has a large hollow metal sphere of radius ‘R’ with a charge ‘Q’ evenly spread over its surface. This sphere is mounted on an insulating column.
The potential (Vr1) at the surface of the larger sphere due to the charge ‘Q’ is given by:
\(\displaystyle V_{r1} = \frac{1}{4\pi\epsilon_0} \cdot \frac{Q}{R}\)
where (\(\displaystyle \epsilon_0 \)) is the permittivity of free space.
Now, imagine a smaller sphere of radius ‘r’ and surface charge ‘q’ placed inside the larger sphere. The potential (Vr2) due to the smaller sphere is:
\(\displaystyle V_{r2} = \frac{1}{4\pi\epsilon_0} \cdot \frac{q}{r}\)
The total potential at the surface of the larger sphere, considering both charges, is:
\(\displaystyle V_R = \frac{1}{4\pi\epsilon_0} \cdot \left( \frac{q}{R} + \frac{Q}{R} \right)\)
The potential at the surface of the smaller sphere is:
\(\displaystyle V_r = \frac{1}{4\pi\epsilon_0} \cdot \left( \frac{q}{r} + \frac{Q}{R} \right)\)
The potential difference between the two spheres is:
\(\displaystyle V_R – V_r = \frac{q}{4\pi\epsilon_0} \left( \frac{1}{R} – \frac{1}{r} \right)\)
Assuming ‘q’ is positive, the inner sphere remains at a higher potential than the outer sphere, making (VR – Vr) always positive.
If the smaller sphere is connected to the larger sphere, the charge ‘q’ gets transferred to the larger sphere, increasing its charge and potential.
As the charge ‘q’ is transferred to the larger sphere, the new potential of the larger sphere becomes:
\(\displaystyle V_{new} = \frac{1}{4\pi\epsilon_0} \cdot \frac{Q + q}{R}\)
This shows that the potential of the larger sphere increases as the charge is transferred to it.
The Van de Graaff Generator accumulates charge on the outer sphere, increasing its potential. This process can continue, adding more charge to the sphere and thereby increasing its potential energy. It’s a practical demonstration of how charge quantization and electrostatic principles can be harnessed to create high voltages.
Van de Graaff Generator as a Particle Accelerator
A particle accelerator is a machine that speeds up charged particles, like protons or electrons, to incredibly high speeds. The Van de Graaff Generator can act as a simple particle accelerator.
High Voltage Creation: The Van de Graaff Generator creates a very high electric potential, often in the order of a few million volts. This is achieved by the movement of a belt that accumulates charge on a hollow metal sphere.
Electric Field and Acceleration: This high voltage results in a very large electric field around the sphere. An electric field exerts a force on charged particles within it. The stronger the field, the greater the force on the particles.
Charged Particles: In a particle accelerator, we introduce charged particles like protons or electrons. These particles are naturally attracted to or repelled by the charged sphere, depending on their charge.
Acceleration Process: The electric field created by the Van de Graaff Generator will push or pull the charged particles, causing them to accelerate. The particles gain kinetic energy as they are accelerated by the electric field.
Particle Collision: Once the particles are accelerated to high speeds, they can be directed toward a target or used in collision experiments. In these collisions, scientists can study the fundamental properties of matter.
Van de Graaff Generators were used in early particle physics research to accelerate particles before the development of more powerful accelerators like cyclotrons and synchrotrons.
A Van de Graaff Generator can be used as a particle accelerator because it can create a high electric potential that generates a strong electric field. This field can then accelerate charged particles to high speeds, allowing physicists to conduct experiments that reveal the inner workings of atoms and subatomic particles.
Advantages of Van de Graaff Generator
High Voltage Generation: The Van de Graaff Generator can create very high voltages, often in the order of millions of volts. This is particularly useful in physics experiments where high energy is required to accelerate particles.
Ripple-Free Output: Unlike many other generators, the output of a Van de Graaff Generator is steady and ripple-free. This means the voltage it produces does not fluctuate, which is ideal for precise scientific work.
Flexibility and Precision of Voltage Control: The voltage produced by a Van de Graaff Generator can be precisely controlled, allowing for flexibility in various experimental setups. This precision is crucial for experiments that require specific voltage levels.
Simplicity of Design: Its design is relatively simple and does not involve complex machinery. This makes it easier to understand, maintain, and repair if necessary.
Educational Value: Van de Graaff Generators are often used in classrooms to demonstrate the principles of electrostatics. They can create visual effects like sparks, which help students visualize and understand electric charges and fields.
Cost-Effective: They are relatively inexpensive to build or purchase compared to other types of generators that can produce similar voltages.
Medical Applications: Van de Graaff Generators have been used in medicine, particularly in radiation therapy for cancer treatment. The high-energy beams they help produce can be used to target and destroy cancerous cells.
The Van de Graaff Generator is a versatile tool in both education and research. Its ability to generate high voltages with precision and without fluctuations makes it an invaluable device in the field of physics and beyond.
Disadvantages of Van de Graaff Generator
Van de Graaff generators are excellent tools for demonstrating electrostatic principles and conducting certain types of experiments, they do have limitations related to current output, environmental sensitivity, maintenance needs, safety, size, and stability. Let’s look in to it,
Limited Current Output: While Van de Graaff generators can produce high voltages, they typically have limited current output. This limitation makes them unsuitable for applications requiring high electrical power.
Sensitivity to Environmental Conditions: The performance of Van de Graaff generators can be significantly affected by environmental conditions, especially humidity. Moisture in the air can cause the charge to leak away, reducing the efficiency of the generator.
Maintenance of the Belt System: The moving belt system, which is essential for the generator’s operation, can be prone to wear and tear. It requires regular maintenance and can be a point of failure.
Safety Concerns: The high voltages generated by Van de Graaff generators can be dangerous if not handled with caution. Proper safety measures must be in place to prevent accidental shocks.
Size and Portability: Larger Van de Graaff generators can be quite bulky and are not easily portable. This can be a disadvantage in settings where space is limited or mobility is required.
Vibration Issues: The belt can produce significant vibrations, making it challenging to establish a stable electric field. This can affect the precision of experiments conducted with the generator.
Charge Leakage: There can be leakage of charge from the conveyor belt, which reduces the potential difference that the generator can achieve.
Belt Velocity Limitations: The speed at which the belt can safely operate is limited due to the tendency for vibration and the risk of wear. This limits the rate at which charge can be transferred to the sphere.
Also Read: Energy Stored In Capacitors
Applications of the Van de Graaff Generator
The Van de Graaff Generator, a device that might look like a big metal ball attached to a tube, is a sophisticated scientific instrument with several applications.
Particle Accelerators: One of the most significant applications of the Van de Graaff Generator is in particle accelerators. It generates high voltages that can accelerate charged particles, such as protons or electrons, to high speeds. These particles can then be used in nuclear physics experiments to study the structure of atoms.
Educational Demonstrations: In classrooms, Van de Graaff Generators are used to demonstrate the principles of electrostatics. When connected to a metal dome, they can create sparks or make hair stand on end, visually showing the effects of static electricity.
Research Laboratories: Researchers use Van de Graaff Generators to study the behavior of charged particles under high electric fields. This research can lead to a better understanding of materials and the development of new technologies.
Medical Applications: In the medical field, Van de Graaff Generators have been used in radiation therapy for cancer treatment. The high-energy beams they help produce can be used to target and destroy cancerous cells.
Electrostatic Discharge Testing: They are also employed in testing the ability of electronic devices to withstand electrostatic discharges. This is important for ensuring the reliability and safety of electronic equipment.
X-ray Production: High voltages from Van de Graaff Generators can be used to produce X-rays, which are useful in both medical imaging and industrial inspection.
Nuclear Research: In nuclear research, they can be used to initiate nuclear reactions by bombarding targets with high-speed particles.
The Van de Graaff Generator is more than just a tool for making your hair stand up. It’s a versatile device that plays a crucial role in scientific research, education, medicine, and industry, showcasing the power and potential of electrostatic forces.
Solved Examples
Problem 1: A Van de Graaff generator with a spherical dome of radius (R = 0.5 m) is charged to a potential of (\(\displaystyle 5 \times 10^6 \, \text{V}\) ). Calculate the electric field just outside the surface of the dome.
Solution: The electric field (E) just outside the surface of a spherical conductor charged to a potential ( V ) is given by:
\(\displaystyle E = \frac{V}{R} \)
Calculate (E):
\(\displaystyle E = \frac{5 \times 10^6}{0.5} \)
\(\displaystyle E = 1 \times 10^7 \, \text{V/m} \)
Therefore, the electric field just outside the dome’s surface is ( \(\displaystyle 1 \times 10^7 \, \text{V/m} \)).
Problem 2: A Van de Graaff generator with a dome of radius (1 m) holds a charge of (10-5 C). Calculate the potential on the surface of the dome.
Solution: The potential (V) on the surface of a spherical conductor with radius (R) and charge (Q) is given by:
\(\displaystyle V = \frac{Q}{4 \pi \epsilon_0 R} \)
Calculate (V):
\(\displaystyle V = \frac{10^{-5}}{4 \pi \times 8.854 \times 10^{-12} \times 1} \)
\(\displaystyle V = \frac{10^{-5}}{1.112 \times 10^{-10}} \)
\(\displaystyle V = 8.99 \times 10^4 \, \text{V} \)
Therefore, the potential on the dome’s surface is (\(\displaystyle 8.99 \times 10^4 \, \text{V}\) ).
Problem 3: A Van de Graaff generator with a dome of radius (0.5 m) is charged to a potential of (\(\displaystyle 2 \times 10^6 \, \text{V}\) ). Calculate the energy stored in the generator.
Solution: The energy (U) stored in a spherical capacitor is given by:
\(\displaystyle U = \frac{1}{2} C V^2 \)
First, calculate the capacitance (C) of a spherical conductor:
\(\displaystyle C = 4 \pi \epsilon_0 R \)
Calculate (C):
\(\displaystyle C = 4 \pi \times 8.854 \times 10^{-12} \times 0.5 \)
\(\displaystyle C = 2 \pi \times 8.854 \times 10^{-12} \)
\(\displaystyle C = 5.57 \times 10^{-11} \, \text{F} \)
Now, calculate the energy (U):
\(\displaystyle U = \frac{1}{2} \times 5.57 \times 10^{-11} \times (2 \times 10^6)^2 \)
\(\displaystyle U = \frac{1}{2} \times 5.57 \times 10^{-11} \times 4 \times 10^{12} \)
\(\displaystyle U = 1.114 \times 10^2 \, \text{J} \)
Therefore, the energy stored in the generator is (111.4 J).
Problem 4: Two Van de Graaff generators, one with a dome radius of (1 m) and the other with a dome radius of (0.5 m), are charged to the same potential difference of (\(\displaystyle 3 \times 10^6 \, \text{V} \)). Calculate the ratio of their stored energies.
Solution: The energy stored in each generator is given by:
\(\displaystyle U = \frac{1}{2} C V^2 \)
The capacitance of a spherical conductor is:
\(\displaystyle C = 4 \pi \epsilon_0 R \)
Let the energy stored in the generator with radius (R1 = 1 m) be (U1) and the energy stored in the generator with radius (R2 = 0.5 m) be (U2).
Calculate the capacitances:
\(\displaystyle C_1 = 4 \pi \epsilon_0 R_1 = 4 \pi \times 8.854 \times 10^{-12} \times 1 \)
\(\displaystyle C_1 = 1.112 \times 10^{-10} \, \text{F} \)
\(\displaystyle C_2 = 4 \pi \epsilon_0 R_2 = 4 \pi \times 8.854 \times 10^{-12} \times 0.5 \)
\(\displaystyle C_2 = 5.57 \times 10^{-11} \, \text{F}\)
Calculate the stored energies:
\(\displaystyle U_1 = \frac{1}{2} C_1 V^2 = \frac{1}{2} \times 1.112 \times 10^{-10} \times (3 \times 10^6)^2\)
\(\displaystyle U_1 = \frac{1}{2} \times 1.112 \times 10^{-10} \times 9 \times 10^{12} \)
\(\displaystyle U_1 = 5.004 \times 10^2 \, \text{J} \)
\(\displaystyle U_2 = \frac{1}{2} C_2 V^2 = \frac{1}{2} \times 5.57 \times 10^{-11} \times (3 \times 10^6)^2 \)
\(\displaystyle U_2 = \frac{1}{2} \times 5.57 \times 10^{-11} \times 9 \times 10^{12} \)
\(\displaystyle U_2 = 2.502 \times 10^2 \, \text{J} \)
The ratio of the stored energies is:
\(\displaystyle \frac{U_1}{U_2} = \frac{5.004 \times 10^2}{2.502 \times 10^2} \)
\(\displaystyle \frac{U_1}{U_2} = 2 \)
Therefore, the ratio of the stored energies is 2:1.
Problem 5: A Van de Graaff generator accelerates a proton (charge (\(\displaystyle e = 1.6 \times 10^{-19} \, \text{C}\) ), mass ( \(\displaystyle m = 1.67 \times 10^{-27} \, \text{kg} )\)) through a potential difference of (\(\displaystyle 5 \times 10^6 \, \text{V} \)). Calculate the final speed of the proton.
Solution: The kinetic energy gained by the proton is equal to the work done by the electric field:
\(\displaystyle \frac{1}{2} m v^2 = e V \)
Calculate (v):
\(\displaystyle \frac{1}{2} \times 1.67 \times 10^{-27} \times v^2 = 1.6 \times 10^{-19} \times 5 \times 10^6 \)
\(\displaystyle \frac{1}{2} \times 1.67 \times 10^{-27} \times v^2 = 8 \times 10^{-13} \)
\(\displaystyle v^2 = \frac{2 \times 8 \times 10^{-13}}{1.67 \times 10^{-27}} \)
\(\displaystyle v^2 = \frac{1.6 \times 10^{-12}}{1.67\times 10^{-27}} \)
\(\displaystyle v^2 = 9.58 \times 10^{14} \)
\(\displaystyle v = \sqrt{9.58 \times 10^{14}} \)
\(\displaystyle v \approx 9.79 \times 10^7 \, \text{m/s}\)
Therefore, the final speed of the proton is approximately (\(\displaystyle 9.79 \times 10^7 \, \text{m/s} \)).
Problem 6: A Van de Graaff generator operates in air with a dome radius of (1 m). The breakdown electric field of air is (\(\displaystyle 3 \times 10^6 \, \text{V/m} \)). Calculate the maximum charge that can be stored on the dome.
Solution: The electric field (E) just outside the surface of a spherical conductor is given by:
\(\displaystyle E = \frac{Q}{4 \pi \epsilon_0 R^2} \)
Rearrange to solve for (Q):
\(\displaystyle Q = E \times 4 \pi \epsilon_0 R^2 \)
Calculate (Q):
\(\displaystyle Q = 3 \times 10^6 \times 4 \pi \times 8.854 \times 10^{-12} \times (1)^2 \)
\(\displaystyle Q = 3 \times 10^6 \times 4 \pi \times 8.854 \times 10^{-12} \)
\(\displaystyle Q = 3 \times 4 \pi \times 8.854 \times 10^{-6} \)
\(\displaystyle Q = 3 \times 1.112 \times 10^{-5} \)
\(\displaystyle Q = 3.34 \times 10^{-5} \, \text{C} \)
Therefore, the maximum charge that can be stored on the dome is (\(\displaystyle 3.34 \times 10^{-5} \, \text{C} \)).
Problem 7: A Van de Graaff generator has a spherical dome of radius (R = 1 m). The dome is charged to a potential (VR). Calculate the potential difference between the surface of the dome and a point (r = 2 m) from the center of the dome. Assume the charge on the dome is (\(\displaystyle q = 2 \times 10^{-5} \, \text{C}\) ).
Solution: The potential difference between two points at distances (R) and (r) from a point charge (q) is given by:
\(\displaystyle V_R – V_r = \frac{q}{4 \pi \epsilon_0} \left( \frac{1}{R} – \frac{1}{r} \right) \)
Calculate the potential difference:
\(\displaystyle V_R – V_r = \frac{2 \times 10^{-5}}{4 \pi \times 8.854 \times 10^{-12}} \left( \frac{1}{1} – \frac{1}{2} \right) \)
First, calculate the term inside the parentheses:
\(\displaystyle\frac{1}{1} – \frac{1}{2} = 1 – 0.5 = 0.5 \)
Now calculate the constant factor:
\(\displaystyle \frac{2 \times 10^{-5}}{4 \pi \times 8.854 \times 10^{-12}} \)
\(\displaystyle = \frac{2 \times 10^{-5}}{1.112 \times 10^{-10}} \)
\(\displaystyle = 1.798 \times 10^5 \, \text{V} \)
Therefore:
\(\displaystyle V_R – V_r = 1.798 \times 10^5 \times 0.5 \)
\(\displaystyle V_R – V_r = 8.99 \times 10^4 \, \text{V} \)
Therefore, the potential difference between the surface of the dome and a point (2 m) from the center of the dome is approximately (\(\displaystyle 8.99 \times 10^4 \, \text{V}\) ).
FAQs
What is a Van de Graaff generator and how does it work?
A Van de Graaff generator is an electrostatic machine that generates high voltages by accumulating charge on a large spherical electrode. It works by using a moving belt to transfer electric charge from a lower potential to a higher potential on the sphere, where it accumulates and creates a high voltage.
How is the potential difference created in a Van de Graaff generator?
The potential difference in a Van de Graaff generator is created by continuously transferring charge to the spherical electrode. As more charge accumulates, the potential difference between the sphere and the ground increases, allowing the generator to achieve very high voltages.
What determines the maximum potential of a Van de Graaff generator?
The maximum potential of a Van de Graaff generator is determined by factors such as the size of the spherical electrode, the insulating properties of the belt and supporting structure, and the surrounding environment’s ability to prevent electrical discharge. Larger spheres and better insulation allow for higher maximum potential.
How is the Van de Graaff generator used as a particle accelerator?
The Van de Graaff generator is used as a particle accelerator by utilizing the high voltage it generates to accelerate charged particles. These particles are injected into a vacuum tube, where the high potential difference propels them to high speeds. This setup is used in nuclear physics experiments to study particle interactions.
What are some common applications of the Van de Graaff generator?
Common applications of the Van de Graaff generator include educational demonstrations of electrostatic principles, particle acceleration for nuclear physics research, and generating high voltages for testing electrical insulation and components.
How can the potential of a Van de Graaff generator be measured?
The potential of a Van de Graaff generator can be measured using an electrostatic voltmeter or a calibrated spark gap. The electrostatic voltmeter provides a direct reading of the voltage, while the spark gap can indicate the potential based on the known breakdown voltage of the air gap.
What safety precautions should be taken when operating a Van de Graaff generator?
Safety precautions when operating a Van de Graaff generator include ensuring the area is free of flammable materials, avoiding direct contact with the high-voltage components, grounding the device properly, and using appropriate protective equipment such as insulating gloves and footwear to prevent accidental electric shocks.
